多元复合函数偏导、泰勒公式、多元向量函数、方向导数与梯度

复合函数偏导

链式法则

设函数 $u = \varphi(x),\, v = \psi(x)$ 在 $x$ 处可导，函数 $z = f(u, v)$ 在点 $(u, v)$ 处可微，则复合函数 $z = f(\varphi(x), \psi(x))$ 在点 $x$ 处可导，且有

$$\dfrac{\d z}{\d x} = \dfrac{\pd z}{\pd u} \dfrac{\d u}{\d x} + \dfrac{\pd z}{\pd v} \dfrac{\d v}{\d x}$$

其中 $\dfrac{\d z}{\d x}$ 称为全导数。

---

证明：

对自变量 $x$ 有增量 $\Delta x$，从而引起中间变量 $u,\, v$ 的增量分别为

$$\begin{aligned} \Delta u &= \varphi(x + \Delta x) - \varphi(x)\\ \Delta v &= \psi(x + \Delta x) - \psi(x) \end{aligned}$$

若 $\Delta u = \Delta v = 0$，则 $\Delta z = 0$，显然成立。

若二者不同时为零，由于 $z = f(u, v)$ 可微，有

$$\Delta z = \dfrac{\pd z}{\pd u} \Delta u + \dfrac{\pd z}{\pd v} \Delta v + o(\rho)$$

其中 $\rho = \sqrt{(\Delta u)^2 + (\Delta v)^2}$

从而有

$$\dfrac{\Delta z}{\Delta x} = \dfrac{\pd z}{\pd u} \dfrac{\Delta u}{\Delta x} + \dfrac{\pd z}{\pd v} \dfrac{\Delta v}{\Delta x} + \dfrac{o(\rho)}{\Delta x}$$

令 $\Delta x \to 0$，已知 $u = \varphi(x),\, v = \psi(x)$ 可导，所以有

$$\begin{aligned} \lim_{\Delta x \to 0} \dfrac{\Delta u}{\Delta x} &= \dfrac{\d u}{\d x}\\ \lim_{\Delta x \to 0} \dfrac{\Delta v}{\Delta x} &= \dfrac{\d v}{\d x} \end{aligned}$$

由于 $\lim\limits_{\Delta x \to 0} \Delta u = 0,\, \lim\limits_{\Delta x \to 0} \Delta v = 0$，所以有 $\lim\limits_{\Delta x \to 0} \rho = 0$，从而有

$$\begin{aligned} \lim\limits_{\Delta x \to 0} \dfrac{o(\rho)}{\Delta x} &= \lim\limits_{\Delta x \to 0} \operatorname{sign}(\Delta x) \dfrac{o(\rho)}{\rho} \dfrac{\sqrt{(\Delta u)^2 + (\Delta v)^2}}{\sqrt{(\Delta x)^2}}\\ &= \lim\limits_{\Delta x \to 0} \operatorname{sign}(\Delta x) \dfrac{o(\rho)}{\rho} \sqrt{\left( \dfrac{\Delta u}{\Delta x} \right)^2 + \left( \dfrac{\Delta v}{\Delta x} \right)^2}\\ &= \sqrt{\left( \dfrac{\d u}{\d x} \right)^2 + \left( \dfrac{\d v}{\d x} \right)^2} \lim\limits_{\Delta x \to 0} \operatorname{sign}(\Delta x) \dfrac{o(\rho)}{\rho} \\ &= 0\quad (\text{前面根号和后面 $\operatorname{sign}$ 函数有界，而 $o(\rho)$ 是 $\rho$ 的高阶无穷小}) \end{aligned}$$

从而有

$$\dfrac{\d z}{\d x} = \dfrac{\pd z}{\pd u} \dfrac{\d u}{\d x} + \dfrac{\pd z}{\pd v} \dfrac{\d v}{\d x}$$

设函数 $u = \varphi(x, y),\, v = \psi(x, y)$ 在 $(x, y)$ 处可偏导，函数 $z = f(u, v)$ 在点 $(u, v)$ 处可微，则复合函数 $z = f(\varphi(x, y), \psi(x, y))$ 在点 $(x, y)$ 处可偏导，且有

$$\begin{aligned} \dfrac{\pd z}{\pd x} &= \dfrac{\pd z}{\pd u} \dfrac{\pd u}{\pd x} + \dfrac{\pd z}{\pd v} \dfrac{\pd v}{\pd x}\\ \dfrac{\pd z}{\pd y} &= \dfrac{\pd z}{\pd u} \dfrac{\pd u}{\pd y} + \dfrac{\pd z}{\pd v} \dfrac{\pd v}{\pd y} \end{aligned}$$

---

证明：

分别视 $y,\, x$ 为常数，运用上面的链式法则即得证。

设函数 $u = \varphi(x, y),\, v = \psi(x, y)$ 在 $(x, y)$ 处可偏导，函数 $f(x, y, u, v)$ 在点 $(x, y, u, v)$ 处可微，则复合函数 $z = f(x, y, \varphi(x, y), \psi(x, y))$ 在点 $(x, y)$ 处可偏导，且有

$$\begin{aligned} \dfrac{\pd z}{\pd x} &= \dfrac{\pd f}{\pd x} + \dfrac{\pd f}{\pd u} \dfrac{\pd u}{\pd x} + \dfrac{\pd f}{\pd v} \dfrac{\pd v }{\pd x}\\ \dfrac{\pd z}{\pd y} &= \dfrac{\pd f}{\pd y} + \dfrac{\pd f}{\pd u} \dfrac{\pd u}{\pd y} + \dfrac{\pd f}{\pd v} \dfrac{\pd v }{\pd y} \end{aligned}$$

这里需要指出，$\dfrac{\pd f}{\pd x}$ 的含义是对四元函数（$x,\, y,\, u,\, v$）关于 $x$ 求偏导，而 $\dfrac{\pd z}{\pd x}$ 含义是对二元函数（$x,\, y$）关于 $x$ 求偏导。

抽象，难记。找了个网上的方法。

对于最难记的 Chain-Rule-3，画出下面的图

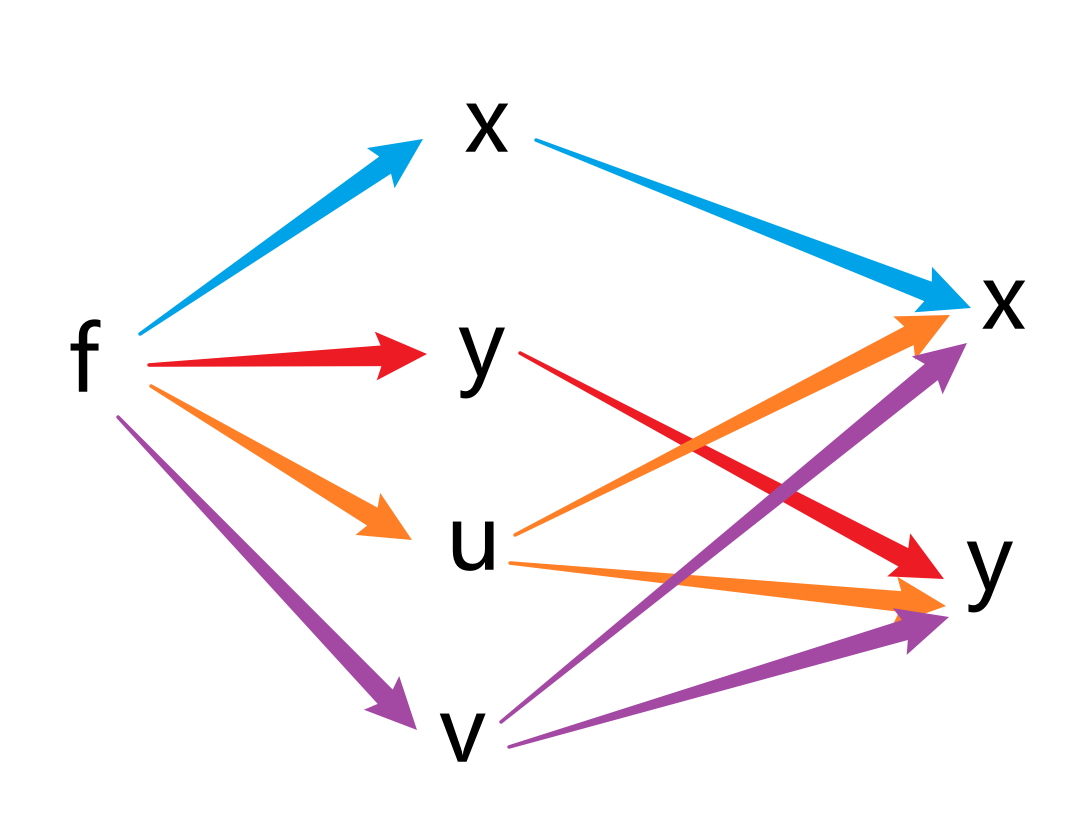
同色箭头相乘，异色箭头相加。下一层超过 $2$ 个变量使用偏导，否则使用导数。对某个独立变量的偏导只需追溯所有最终指向它的箭头。从而有

$$\begin{aligned} \dfrac{\pd z}{\pd x} &= \dfrac{\pd f}{\pd x} \dfrac{\pd x}{\pd x} + \dfrac{\pd f}{\pd u} \dfrac{\pd u}{\pd x} + \dfrac{\pd f}{\pd v} \dfrac{\pd v}{\pd x}\\ &= \dfrac{\pd f}{\pd x} \cdot 1 + \dfrac{\pd f}{\pd u} \dfrac{\pd u}{\pd x} + \dfrac{\pd f}{\pd v} \dfrac{\pd v}{\pd x}\\ &= \dfrac{\pd f}{\pd x} + \dfrac{\pd f}{\pd u} \dfrac{\pd u}{\pd x} + \dfrac{\pd f}{\pd v} \dfrac{\pd v}{\pd x} \end{aligned}$$

隐函数

隐函数存在定理 1

设 $P_0(x_0, y_0) \in \R^2,\, G = N_{\delta}(P_0)$，若

1. 函数 $F$ 在 $G$ 上连续可微
2. $F(P_0) = 0$
3. $F'_y(P_0) \neq 0$

则存在 $x_{0}$ 的邻域 $I=N_{\delta_{1}}\left(x_{0}\right)$ 和唯一的函数 $y=f(x)$ 使得

1. 对任意 $x \in I$，有 $F(x, f(x)) = 0$
2. $f(x_0) = y_0$
3. $f$ 在 $I$ 上连续可微，且有

$$f'(x) = -\dfrac{F'_x(x, y)}{F'_y(x, y)}$$

利用上面讲的方法，对隐函数方程两侧求导有

$$\dfrac{\pd F}{\pd x} \dfrac{\d x}{\d x} + \dfrac{\pd F}{\pd y} \dfrac{\d y}{\d x} = 0$$

从而得到

$$\begin{aligned} \dfrac{\d y}{\d x} &= -\dfrac{\frac{\pd F}{\pd x}}{\frac{\pd F}{\pd y}}\\ &= -\dfrac{F'_x(x, y)}{F'_y(x, y)} \end{aligned}$$

同理对三元函数有

隐函数存在定理 2

设 $P_0(x_0, y_0, z_0) \in \R^3,\, G = N_{\delta}(P_0)$，若

1. 函数 $F$ 在 $G$ 上连续可微
2. $F(P_0) = 0$
3. $F'_z(P_0) \neq 0$

则存在 $U = \left\lbrace (x, y) \mid \left\lvert x - x_0 \right\rvert < h, \left\lvert y - y_0 \right\rvert < k \right\rbrace$ 和唯一的函数 $z=f(x, y)$ 使得

1. 对任意 $(x, y) \in U$，有 $F(x, y, f(x, y)) = 0$
2. $f(x_0, y_0) = z_0$
3. $f$ 在 $U$ 上连续可微，且有

$$\begin{aligned} \dfrac{\pd f}{\pd x} = -\dfrac{F'_x(x, y, z)}{F'_z(x, y, z)},\quad \dfrac{\pd f}{\pd y} = -\dfrac{F'_y(x, y, z)}{F'_z(x, y, z)} \end{aligned}$$

需要注意的一点，偏导不能像导数一样看成是微分的商（微商），偏导数记号 $\dfrac{\pd z}{\pd x}$ 是一个整体。下面用一个例子进行具体解释。

对于隐函数 $F(x, y, z) = 0$，且其满足隐函数存在定理条件，同时有 $F'_x,\, F'_y,\, F'_z$ 都不为零，那么根据隐函数存在定理 2，有

$$\dfrac{\pd z}{\pd x} \dfrac{\pd x}{\pd y} \dfrac{\pd y}{\pd z} = \left( - \dfrac{F'_x}{F'_z} \right) \left( - \dfrac{F'_y}{F'_x} \right) \left( - \dfrac{F'_z}{F'_y} \right) = -1$$

而非

$$\begin{aligned} \dfrac{\pd z}{\pd x} \dfrac{\pd x}{\pd y} \dfrac{\pd y}{\pd z} &= \dfrac{\pd z}{\bcancel{\pd x}} \dfrac{\bcancel{\pd x}}{\pd y} \dfrac{\pd y}{\pd z}\\ \phantom{\text{写着玩，}} &= \dfrac{\pd z}{\bcancel{\pd y}} \dfrac{\bcancel{\pd y}}{\pd z}\\ \phantom{\text{只是玩玩}} &= \dfrac{\bcancel{\pd z}}{\bcancel{\pd z}}\\ \phantom{\text{conceal}} &= 1 \end{aligned}$$

我的理解是，偏导是成对存在的，不存在像微分这样单独的记号，也就是说没有 $\pd x$ 这样的记号，因为并不知道这个玩意的含义是什么。但是却有 $\d x$ 这样的记号，因为微分是有明确的含义的。

对于方程组，有

隐函数存在定理 3

设 $P_0(x_0, y_0, u_0, v_0) \in \R^4,\, G = N_{\delta}(P_0)$，若

1. 函数 $F,\, H$ 在 $G$ 上连续可微
2. $F(P_0) = H(P_0) = 0$
3. 雅可比行列式（Jacobi Determinant）

$$J = \dfrac{D(F, H)}{D(u, v)} = \begin{vmatrix} F'_u & F'_v\\ H'_u & H'_v \end{vmatrix}_{P_0} \ne 0$$

则存在 $U=\left\{(x, y)\mid |x-x_{0}|<h, | y-y_{0} | <k\right\}$ 和唯一一组函数 $u=u(x, y), v=v(x, y)$，使得

1. 对任意 $(x, y) \in U$，有 $F(x, y, u(x, y), v(x, y))=0, H(x, y, u(x, y), v(x, y))=0$
2. $u(x_0, y_0) = u_0, v(x_0, y_0) = v_0$
3. $u, v$ 在 $U$ 上连续可微，且有

$$\begin{aligned} \dfrac{\pd u}{\pd x} &= -\dfrac{\frac{D(F, H)}{D(x, v)}}{J},\quad \dfrac{\pd u}{\pd y} &= -\dfrac{\frac{D(F, H)}{D(y, v)}}{J}\\ \dfrac{\pd v}{\pd x} &= -\dfrac{\frac{D(F, H)}{D(u, x)}}{J},\quad \dfrac{\pd v}{\pd y} &= -\dfrac{\frac{D(F, H)}{D(u, y)}}{J} \end{aligned}$$

查阅了相关资料，为了更好地理解上面的定理，引入雅可比矩阵。

设 $\bm{f}\colon\R^n \to \R^m$，定义 $\bm{f}$ 的雅可比矩阵 $\bm{J}$ 为代表 $\bm{f}$ 的从 $\R^n$ 到 $\R^m$ 的线性变换的矩阵。

则 $\bm{J}$ 为 $m \times n$ 阶矩阵，且有 $\bm{J}_{ij} = \dfrac{\pd f_i}{\pd x_j}$，即

$$\bm{J} = \begin{bmatrix} \dfrac{\pd \bm{f}}{\pd x_1} & \cdots & \dfrac{\pd \bm{f}}{\pd x_n} \end{bmatrix} = \begin{bmatrix} \dfrac{\pd f_1}{\pd x_1} & \cdots & \dfrac{\pd f_1}{\pd x_n}\\ \vdots & \ddots & \vdots\\ \dfrac{\pd f_m}{\pd x_1} & \cdots & \dfrac{\pd f_m}{\pd x_n} \end{bmatrix}$$

还是不太好看懂，重新理解一下多元函数。

先从简单的出发，设二元函数 $\bm{f} \colon \R^2 \to \R^2$，可以看作是 $(u, v) \to (F, G)$，其中 $F, G\colon \R^2 \to \R$。

令 $P(u, v),\, Q(F, G)$，从而有

$$\d F = \dfrac{\pd F}{\pd u} \d u + \dfrac{\pd F}{\pd v} \d v,\quad \d G = \dfrac{\pd G}{\pd u} \d u + \dfrac{\pd G}{\pd v} \d v$$

写成向量形式，即

$$\begin{aligned} \begin{bmatrix} \d F\\ \d G \end{bmatrix} &= \d u \begin{bmatrix} \dfrac{\pd F}{\pd u}\\ \dfrac{\pd G}{\pd u} \end{bmatrix} + \d v \begin{bmatrix} \dfrac{\pd F}{\pd v}\\ \dfrac{\pd G}{\pd v} \end{bmatrix}\\ &= \begin{bmatrix} \dfrac{\pd F}{\pd u} & \dfrac{\pd F}{\pd v}\\ \dfrac{\pd G}{\pd u} & \dfrac{\pd G}{\pd v} \end{bmatrix} \begin{bmatrix} \d u\\ \d v \end{bmatrix} \end{aligned}$$

可以发现这个矩阵就是雅可比矩阵，即

$$\d \vec{Q} = \bm{J} \d \vec{P}$$

然后就是多元函数，设 $\bm{f}\colon \R^n \to \R^m$，可以看作是 $\vec{x} \to \vec{y}$，其中 $\vec{x} = (x_1, \cdots, x_n),\, \vec{y} = (y_1, \cdots, y_m)$，且 $y_i = f_i(x_1, \cdots, x_n)$，即 $y_i\colon \R^n \to \R$。

同样的，令 $\vec{x} = (x_1, \cdots, x_n),\, \vec{y} = (y_1, \cdots, y_m)$，从而有

$$\begin{aligned} \d y_1 &= \sum_{i=1}^{n} \dfrac{\pd y_1}{\pd x_i} \d x_i\\ &\vdots\\ \d y_m &= \sum_{i=1}^{n} \dfrac{\pd y_m}{\pd x_i} \d x_i \end{aligned}$$

写成向量形式，即

$$\begin{aligned} \d \vec{y} = \begin{bmatrix} \d y_1 \\ \vdots \\ \d y_m \end{bmatrix} &= \sum_{i=1}^{n} \d x_i \dfrac{\pd \vec{y}}{\pd x_i}\\ &= \sum_{i=1}^{n} \d x_i \begin{bmatrix} \dfrac{\pd y_1}{\pd x_i} \\ \vdots \\ \dfrac{\pd y_m}{\pd x_i} \end{bmatrix}\\ &= \begin{bmatrix} \dfrac{\pd y_1}{\pd x_1} & \cdots & \dfrac{\pd y_1}{\pd x_n}\\ \vdots & \ddots & \vdots\\ \dfrac{\pd y_m}{\pd x_1} & \cdots & \dfrac{\pd y_m}{\pd x_n} \end{bmatrix} \begin{bmatrix} \d x_1\\ \vdots\\ \d x_n \end{bmatrix}\\ &= \bm{J} \d \vec{x} \end{aligned}$$

再去看看多元函数的复合函数。设 $\bm{f}\colon \R^n \to \R^m,\, \bm{g}\colon \R^m \to \R^l$，则有 $\bm{g} \circ \bm{f}\colon \R^n \to \R^l$，即 $\vec{x} \to \vec{z}$，其中 $\vec{z} = \bm{g}(\bm{f}(\vec{x}))$。

$$\begin{aligned} \d \vec{z} &= \bm{J}_{\bm{g}} \d \vec{y}\\ &= \bm{J}_{\bm{g}} \bm{J}_{\bm{f}} \d \vec{x}\\ \end{aligned}$$

写到这，我陷入了沉思，这与隐函数存在定理 3 有关联吗，我好像只是理解了一下雅可比矩阵的意义。没草稿纸（懒得拿），试着像定理 1 一样尝试理解内涵。

还好只有两个方程，即

$$\begin{cases} F(x, y, u, v) = 0\\ H(x, y, u, v) = 0 \end{cases}$$

先对 $x$ 求偏导得

$$\begin{cases} \dfrac{\pd F}{\pd x} + \dfrac{\pd F}{\pd u} \dfrac{\pd u}{\pd x} + \dfrac{\pd F}{\pd v} \dfrac{\pd v}{\pd x} &= 0\\ \dfrac{\pd H}{\pd x} + \dfrac{\pd H}{\pd u} \dfrac{\pd u}{\pd x} + \dfrac{\pd H}{\pd v} \dfrac{\pd v}{\pd x} &= 0 \end{cases}$$

不是很清晰，我稍微调换一下位置，然后高亮一些部分

$$\begin{cases} \dfrac{\pd F}{\pd u} \textcolor{FF0099}{\dfrac{\pd u}{\pd x}} + \dfrac{\pd F}{\pd v} \textcolor{0099FF}{\dfrac{\pd v}{\pd x}} &= -\dfrac{\pd F}{\pd x}\\ \dfrac{\pd H}{\pd u} \textcolor{FF0099}{\dfrac{\pd u}{\pd x}} + \dfrac{\pd H}{\pd v} \textcolor{0099FF}{\dfrac{\pd v}{\pd x}} &= -\dfrac{\pd H}{\pd x} \end{cases}$$

这下就是线代学过最简单的二元一次方程组了，使用克莱姆法则，同时注意到分母的行列式是

$$\begin{vmatrix} \dfrac{\pd F}{\pd u} & \dfrac{\pd F}{\pd v} \\ \dfrac{\pd H}{\pd u} & \dfrac{\pd H}{\pd v} \end{vmatrix}$$

这不是巧了吗，正好是雅可比行列式。然后这学期没线代，只记得个分母了，差点忘了克莱姆法则怎么弄，想着形式感觉不大对，还拿出草稿纸准备算算。

对于某一列变量，使用等号右侧的值替代掉行列式的那一列系数，那么就有两个行列式

$$-\begin{vmatrix} \dfrac{\pd F}{\pd x} & \dfrac{\pd F}{\pd v} \\ \dfrac{\pd H}{\pd x} & \dfrac{\pd H}{\pd v} \end{vmatrix},\quad -\begin{vmatrix} \dfrac{\pd F}{\pd u} & \dfrac{\pd F}{\pd x} \\ \dfrac{\pd H}{\pd u} & \dfrac{\pd H}{\pd x} \end{vmatrix}$$

这也正好就分别是 $-\dfrac{D(F, H)}{D(x, v)}$ 和 $-\dfrac{D(F, H)}{D(u, x)}$（这个记号的含义是什么我也不清楚，教材用了这个，网上一些资料还用 $-\dfrac{\pd(F, H)}{\pd(x, v)}$），然后就是隐函数存在定理 3 的结论了。

理解了过程，也就方便进行记忆了（并不，还是蛮难记的）。

下面再补充一点，只不过要是觉得写的不好就删掉了。

写到方程组就直接用克莱姆法则解出来了，没啥意思，用矩阵表示看看会不会有什么新发现（没有就删了）。

$$\begin{bmatrix} \dfrac{\pd F}{\pd u} & \dfrac{\pd F}{\pd v} \\ \dfrac{\pd H}{\pd u} & \dfrac{\pd H}{\pd v} \end{bmatrix} \begin{bmatrix} \dfrac{\pd u}{\pd x}\\ \dfrac{\pd v}{\pd x} \end{bmatrix} = -\begin{bmatrix} \dfrac{\pd F}{\pd x}\\ \dfrac{\pd H}{\pd x} \end{bmatrix}$$

对 $y$ 的偏导，由于类似，我上面进行了省略，而用矩阵表示的话，就可以添加回来，变成

$$\begin{bmatrix} \dfrac{\pd F}{\pd u} & \dfrac{\pd F}{\pd v} \\ \dfrac{\pd H}{\pd u} & \dfrac{\pd H}{\pd v} \end{bmatrix} \begin{bmatrix} \dfrac{\pd u}{\pd x} & \dfrac{\pd u}{\pd y}\\ \dfrac{\pd v}{\pd x} & \dfrac{\pd v}{\pd y} \end{bmatrix} = -\begin{bmatrix} \dfrac{\pd F}{\pd x} & \dfrac{\pd F}{\pd y}\\ \dfrac{\pd H}{\pd x} & \dfrac{\pd H}{\pd y} \end{bmatrix}$$

从而有

$$\begin{bmatrix} \dfrac{\pd u}{\pd x} & \dfrac{\pd u}{\pd y}\\ \dfrac{\pd v}{\pd x} & \dfrac{\pd v}{\pd y} \end{bmatrix} = -\begin{bmatrix} \dfrac{\pd F}{\pd u} & \dfrac{\pd F}{\pd v} \\ \dfrac{\pd H}{\pd u} & \dfrac{\pd H}{\pd v} \end{bmatrix}^{-1} \begin{bmatrix} \dfrac{\pd F}{\pd x} & \dfrac{\pd F}{\pd y}\\ \dfrac{\pd H}{\pd x} & \dfrac{\pd H}{\pd y} \end{bmatrix}$$

出现了，雅可比矩阵的逆！这让我想到了什么呢？嗯……什么也没有。那就到此结束吧。

另外对于函数 $\bm{F}\colon \R^n \to \R^n$ 及其雅可比矩阵 $\bm{J}$，有其反函数 $\bm{F}^{-1}$ 与雅可比矩阵 $\bm{J}'$，从而因 $\bm{F} \circ \bm{F}^{-1} = \iota$，从而有 $\bm{J} \bm{J}' = \bm{I}$，即 $\bm{J}' = \bm{J}^{-1}$。更进一步地，有 $J' = \dfrac{1}{J}$。

这为计算雅可比行列式提供了便利，例如后面重积分换元积分需要计算诸如 $J(u, v) = \dfrac{D(x, y)}{D(u, v)}$ 的雅可比行列式，只需计算 $\dfrac{D(u, v)}{D(x, y)}$ 即可。

多元函数泰勒公式

二元函数的泰勒公式

设 $(x_0, y_0) \in \mathbb{R}^{2}$，函数 $f$ 在点 $(x_0, y_0)$ 的某邻域 $G$ 内 $n+1$ 阶连续可微，则对任意 $(x, y) \in G$，有

$$f(x, y)=\sum_{k=0}^{n} \frac{1}{k !}\left(\Delta x \frac{\partial}{\partial x}+\Delta y \frac{\partial}{\partial y}\right)^{k} f(x_0, y_0)+R_{n} \tag{1}$$

这里

$$\begin{aligned} R_{n}=\frac{1}{(n+1) !}\left(\Delta x \frac{\partial}{\partial x}+\Delta y \frac{\partial}{\partial y}\right)^{n+1} f(x_0+\theta \Delta x, y_0+\theta \Delta y), \\ \Delta x=x-x_0, \Delta y=y-y_0 \quad(0<\theta<1) . \end{aligned}$$

式 $(1)$ 称为 $f(x, y)$ 在点 $(x_0, y_0)$ 处的 $n$ 阶泰勒公式，$R_{n}$ 称为泰勒公式的拉格朗日余项余项。

$$\begin{aligned} \left( \Delta x \dfrac{\pd }{\pd x} + \Delta \dfrac{\pd }{\pd y} \right)^k &= \sum_{s=0}^k \binom{k}{s} \Delta x^{k-s} \Delta y^s \dfrac{\pd^k}{\pd x^{k-s} \pd y^s} \\ \end{aligned}$$

---

证明：

取辅助函数

$$F(t)=f(x_0+t \Delta x, y_0+t \Delta y) \quad(0 \le t \le 1)$$

既然 $f$ 在点 $(x_0, y_0)$ 的某邻域 $G$ 内 $n+1$ 阶连续可微，那么 $F$ 在 $[0, 1]$ 上 $n+1$ 阶连续可微。根据一元函数的泰勒公式，有

$$\begin{aligned} F(0) &= f(x_0, y_0)\\ F'(0) &= \dfrac{\d f}{\d t}\as_{t=0} = \dfrac{\pd f}{\pd x} \dfrac{\d x}{\d t} + \dfrac{\pd f}{\pd y} \dfrac{\d y}{\d t}\as_{t=0}\\ &= \Delta x \dfrac{\pd f}{\pd x} + \Delta y \dfrac{\pd f}{\pd y}\as_{(x_0, y_0)}\\ &= \left( \Delta x \dfrac{\pd }{\pd x} + \Delta y\dfrac{\pd }{\pd y} \right) f(x_0, y_0)\\ &\vdots\\ F^{(n)}(0) &= \dfrac{\d^n f}{\d t^n}\as_{t=0} = \sum_{s = 0}^{n} \dfrac{1}{\d t^n} \left( \d x \dfrac{\pd }{\pd x} + \d y \dfrac{\pd }{\pd y} \right)^n f(x_0, y_0)\\ &= \sum_{s = 0}^{n} \left( \dfrac{\d x}{\d t} \dfrac{\pd }{\pd x} + \dfrac{\d y}{\d t}\dfrac{\pd }{\pd y} \right)^n f(x_0, y_0)\\ &= \sum_{s = 0}^{n} \left( \Delta x \dfrac{\pd }{\pd x} + \Delta y\dfrac{\pd }{\pd y} \right)^n f(x_0, y_0)\\ \end{aligned}$$

然后就是一元函数的泰勒公式了

$$\begin{aligned} F(t) &= \sum_{k=0}^n \dfrac{1}{k!}F^{(k)}(0) t^k + R_n(t)\\ &= \sum_{k=0}^n \dfrac{1}{k!} \left( \Delta x \dfrac{\pd }{\pd x} + \Delta y \dfrac{\pd }{\pd y} \right)^k f(x_0, y_0) t^k + R_n(t) \end{aligned}$$

代入 $t=1$ 即得证。

对比一元函数泰勒公式，辅助记忆

$$\begin{aligned} f(x) &= \sum_{k=0}^n \dfrac{f^{(k)}(x_0)}{k!} \Delta x^k + R_n(x) \end{aligned}$$

其中 $R_n(x) = \dfrac{f^{(n + 1)}(\xi)}{(n + 1)!}\Delta x^{n+1}$，$\xi$ 介于 $x$ 与 $x_0$ 之间。

二元函数拉格朗日中值公式

令 $n = 0$，有

$$f(x, y)=f(a, b)+f_{x}^{\prime}(\xi, \eta)(x-a)+f_{y}^{\prime}(\xi, \eta)(y-b)$$

其中 $\xi=a+\theta(x-a), \eta=b+\theta(y-b) \quad(0<\theta<1)$。

多元向量函数

设 $D \subseteq \R^n$，函数 $f, g, h$ 是定义在 $D$ 上的 $n$ 元函数，称

$$\begin{aligned} \bm{A}(x_1, x_2, \cdots, x_n) = \Big( &f(x_1, x_2, \cdots, x_n), \\ &g(x_1, x_2, \cdots, x_n), \\ &h(x_1, x_2, \cdots, x_n) \Big) \end{aligned}$$

为三维空间 $\R^3$ 的 $n$ 元向量函数。

记得在上篇提过……

设二元向量函数

$$\bm{r}(u, v) = \Big( x(u, v), y(u, v), z(u, v) \Big)$$

其中 $(u, v) \in G,\, G \subseteq \R^2$，设 $(u_0, v_0)$ 是 $G$ 的聚点，若存在 $\bm{a} \in \R^3$ 使得

$$\lim_{(u, v) \to (u_0, v_0)} \left\lvert \bm{r}(u, v) - \bm{a} \right\rvert = 0$$

则称向量函数 $\bm{r}(u, v)$ 在 $(u, v) \to (u_0, v_0)$ 时以 $\bm{a}$ 为极限，记作

$$\lim_{(u, v) \to (u_0, v_0)} \bm{r}(u, v) = \bm{a}$$

向量函数 $\bm{r}(u, v)=\Big(x(u, v), y(u, v), z(u, v)\Big)$ 在 $(u, v) \to\left(u_{0}, v_{0}\right)$ 时以 $\bm{a}=$ $\left(a_{1}, a_{2}, a_{3}\right)$ 为极限的充要条件是

$$\lim\limits_{(u, v) \to (u_0, v_0)} x(u, v) = a_1, \quad \lim\limits_{(u, v) \to (u_0, v_0)} y(u, v) = a_2, \quad \lim\limits_{(u, v) \to (u_0, v_0)} z(u, v) = a_3$$

设二元向量函数

$$\bm{r}(u, v) = \Big( x(u, v), y(u, v), z(u, v) \Big)$$

在点 $(u, v)$ 的某邻域内有定义，若极限

$$\lim_{\Delta u \to 0} \frac{\bm{r}(u + \Delta u, v) - \bm{r}(u, v)}{\Delta u}$$

存在，则称此极限为 $\bm{r}(u, v)$ 对 $u$ 的偏导数，记作 $\dfrac{\partial \bm{r}}{\partial u}$ 或 $\bm{r}_u'(u, v)$。

设二元向量函数

$$\bm{r}(u, v) = \Big( x(u, v), y(u, v), z(u, v) \Big)$$

在点 $(u, v)$ 的某邻域内有定义，函数 $x(u, v),\, y(u, v),\, z(u, v)$ 在点 $(u, v)$ 处对 $u$ 的偏导数存在，则向量函数 $\bm{r}(u, v)$ 在 $(u, v)$ 处对 $u$ 的偏导数存在，且

$$\bm{r}_u' = \Big( x_u'(u, v), y_u'(u, v), z_u'(u, v) \Big)$$

方向导数

设 $P_0 \in \R^3$，函数 $f$ 在 $P_0$ 的某邻域内有定义，$\bm{l}$ 是 $\R^3$ 中的一个非零向量，且 $\forall P \in U$，都有 $\overrightarrow{P_0P}$ 与 $\bm{l}$ 的方向相同，若

$$\lim\limits_{P \to P_0} \frac{f(P) - f(P_0)}{\lvert \overrightarrow{P_0P} \rvert}$$

存在，则称此极限为函数 $f$ 在点 $P_0$ 沿方向 $\bm{l}$ 的方向导数，记作 $\dfrac{\pd f}{\pd \bm{l}}(P_0)$。

方向导数都存在无法推出可偏导（大概是因为同一个方向上正向负向可以存在而不同，而偏导要求在那个方向上正向负向存在且相等）；可偏导无法推出方向导数都存在。

函数可偏导只能推出该函数沿坐标轴方向的方向导数存在，而不能推出该函数沿其他方向的方向导数存在。

设函数 $f(x, y, z)$ 在 $(x, y, z)$ 处可微，向量 $\bm{l}$ 的方向余弦分别为 $\cos \alpha, \cos \beta, \cos \gamma$，则函数 $f(x, y, z)$ 在点 $(x, y, z)$ 沿方向 $\bm{l}$ 的方向导数为

$$\frac{\pd f}{\pd \bm{l}}(x, y, z) = f_x'(x, y, z) \cos \alpha + f_y'(x, y, z) \cos \beta + f_z'(x, y, z) \cos \gamma$$

---

证明：

链式法则有

$$\begin{aligned} \dfrac{\pd f}{\pd \bm{l}}(\bm{x}) &= \dfrac{\d }{\d t}\as_{t = 0} f(\bm{x} + t\bm{l}) \\ &= \dfrac{\d }{\d t}\as_{t = 0} f(x + t\cos \alpha, y + t\cos \beta, z + t\cos \gamma) \\ &= f_x'(x, y, z) \cos \alpha + f_y'(x, y, z) \cos \beta + f_z'(x, y, z) \cos \gamma \end{aligned}$$

梯度

上面最后一个定理可以写成

$$\grad f \boldsymbol{\cdot} \bm{l}$$

其中

$$\grad f = \left( \dfrac{\pd f}{\pd x}, \dfrac{\pd f}{\pd y}, \dfrac{\pd f}{\pd z} \right)$$

称为函数 $f(x, y, z)$ 的梯度（Gradient），记作 $\grad f$ 或 $\operatorname{grad} f$ 或 $\dfrac{\pd f}{\pd x} \bm{i} + \dfrac{\pd f}{\pd y} \bm{j} + \dfrac{\pd f}{\pd z} \bm{k}$。

沿梯度方向，函数方向导数取得最大值，且最大值为梯度的模。

---

因为方向导数

$$\begin{aligned} \dfrac{\pd f}{\pd \bm{l}} &= \grad f \boldsymbol{\cdot} \bm{l}\\ &= \lvert \grad f \rvert \cdot \cos \theta \end{aligned}$$

其中 $\theta$ 为 $\grad f$ 与 $\bm{l}$ 的夹角，所以 $\lvert \grad f \rvert$ 为最大值，在 $\theta = 0$ 时取得。