第一类曲线积分
定义
在光滑平面曲线 C C C f ( x , y ) f(x, y) f ( x , y ) C C C 第一类曲线积分 (对弧长的积分 )为
∫ C f ( x , y ) d s = lim λ → 0 ∑ i = 1 n f ( ξ i , η i ) Δ s i \int_C f(x, y) \d s = \lim\limits_{\lambda \to 0} \sum_{i=1}^n f(\xi_i, \eta_i) \Delta s_i
∫ C f ( x , y ) d s = λ → 0 lim i = 1 ∑ n f ( ξ i , η i ) Δ s i
其中 Δ s i \Delta s_i Δ s i C C C i i i ( ξ i , η i ) (\xi_i, \eta_i) ( ξ i , η i ) λ \lambda λ C C C
其中 f ( x , y ) f(x, y) f ( x , y ) 被积函数 ,C C C 积分曲线 , d s \d s d s 弧微分 ( d s > 0 \d s > 0 d s > 0
类似的有空间曲线上的第一类曲线积分:
∫ C f ( x , y , z ) d s = lim λ → 0 ∑ i = 1 n f ( ξ i , η i , ζ i ) Δ s i \int_C f(x, y, z) \d s = \lim\limits_{\lambda \to 0} \sum_{i=1}^n f(\xi_i, \eta_i, \zeta_i) \Delta s_i
∫ C f ( x , y , z ) d s = λ → 0 lim i = 1 ∑ n f ( ξ i , η i , ζ i ) Δ s i
积分性质与定积分类似。特别地,有
∫ A B ^ f ( x , y ) d s = ∫ B A ^ f ( x , y ) d s ∫ C f ( x , y ) d s = ∫ − C f ( x , y ) d s \begin{aligned}
\int_{\widehat{AB}} f(x, y) \d s &= \int_{\widehat{BA}} f(x, y) \d s\\
\int_C f(x, y) \d s &= \int_{-C} f(x, y) \d s
\end{aligned}
∫ A B f ( x , y ) d s ∫ C f ( x , y ) d s = ∫ B A f ( x , y ) d s = ∫ − C f ( x , y ) d s
其中 − C -C − C C C C
理解成线质量即可。
计算
设 f ( x , y ) f(x, y) f ( x , y ) C C C C C C r ( t ) = ( φ ( t ) , ψ ( t ) ) \bm{r}(t) = \bigl(\varphi(t), \psi(t)\bigr) r ( t ) = ( φ ( t ) , ψ ( t ) )
{ x = φ ( t ) y = ψ ( t ) ( a ⩽ t ⩽ b ) \left\lbrace\begin{aligned}
x &= \varphi(t) \\
y &= \psi(t) \\
\end{aligned}\right. \quad (a \le t \le b)
{ x y = φ ( t ) = ψ ( t ) ( a ⩽ t ⩽ b )
其中 φ ( t ) \varphi(t) φ ( t ) ψ ( t ) \psi(t) ψ ( t ) [ a , b ] [a, b] [ a , b ] [ φ ′ ( t ) ] 2 + [ ψ ′ ( t ) ] 2 ≠ 0 [\varphi'(t)]^2 + [\psi'(t)]^2 \neq 0 [ φ ′ ( t ) ] 2 + [ ψ ′ ( t ) ] 2 = 0 第一类曲线积分 ∫ C f ( x , y ) d s \displaystyle\int_C f(x, y) \d s ∫ C f ( x , y ) d s ,且
∫ C f ( x , y ) d s = ∫ a b f ( φ ( t ) , ψ ( t ) ) ∣ r ′ ( t ) ∣ d t = ∫ a b f ( φ ( t ) , ψ ( t ) ) [ φ ′ ( t ) ] 2 + [ ψ ′ ( t ) ] 2 d t \begin{aligned}
\int_C f(x, y) \d s &= \int_a^b f\bigl(\varphi(t), \psi(t)\bigr) | \bm{r}'(t) | \d t \\
&= \boxed{\int_a^b f\bigl(\varphi(t), \psi(t)\bigr) \sqrt{[\varphi'(t)]^2 + [\psi'(t)]^2} \d t}
\end{aligned}
∫ C f ( x , y ) d s = ∫ a b f ( φ ( t ) , ψ ( t ) ) ∣ r ′ ( t ) ∣ d t = ∫ a b f ( φ ( t ) , ψ ( t ) ) [ φ ′ ( t ) ] 2 + [ ψ ′ ( t ) ] 2 d t
第二类曲线积分
考虑平面光滑曲线 C C C F ( x , y ) \bm{F}(x, y) F ( x , y )
F ( x , y ) = P ( x , y ) i + Q ( x , y ) j \bm{F}(x, y) = P(x, y) \bm{i} + Q(x, y) \bm{j}
F ( x , y ) = P ( x , y ) i + Q ( x , y ) j
则向量场 F ( x , y ) \bm{F}(x, y) F ( x , y ) C C C 第二类曲线积分 (对坐标的曲线积分 )为
∫ C F ( x , y ) ⋅ d r = ∫ C P ( x , y ) d x + Q ( x , y ) d y \int_C \bm{F}(x, y) \boldsymbol{\cdot} \d \bm{r} = \int_C P(x, y) \d x + Q(x, y) \d y
∫ C F ( x , y ) ⋅ d r = ∫ C P ( x , y ) d x + Q ( x , y ) d y
其中 d r = i d x + j d y \d \bm{r} = \bm{i} \d x + \bm{j} \d y d r = i d x + j d y 位矢微分 。曲线 C C C 积分路径 。
特别地,
∫ C P ( x , y ) d x = lim λ → 0 ∑ i = 1 n P ( ξ i , η i ) Δ x i \int_C P(x, y) \d x = \lim\limits_{\lambda \to 0} \sum_{i=1}^n P(\xi_i, \eta_i) \Delta x_i
∫ C P ( x , y ) d x = λ → 0 lim i = 1 ∑ n P ( ξ i , η i ) Δ x i
称为函数 P ( x , y ) P(x, y) P ( x , y ) C C C x x x 。
类似的有空间曲线上的第二类曲线积分:
∫ C F ( x , y , z ) ⋅ d r = ∫ C P ( x , y , z ) d x + Q ( x , y , z ) d y + R ( x , y , z ) d z \int_C \bm{F}(x, y, z) \boldsymbol{\cdot} \d \bm{r} = \int_C P(x, y, z) \d x + Q(x, y, z) \d y + R(x, y, z) \d z
∫ C F ( x , y , z ) ⋅ d r = ∫ C P ( x , y , z ) d x + Q ( x , y , z ) d y + R ( x , y , z ) d z
其中 d r = i d x + j d y + k d z \d \bm{r} = \bm{i} \d x + \bm{j} \d y + \bm{k} \d z d r = i d x + j d y + k d z
积分性质与定积分类似。特别地,有
∫ A B ^ F ( x , y ) ⋅ d r = − ∫ B A ^ F ( x , y ) ⋅ d r ∫ C F ( x , y ) ⋅ d r = − ∫ − C F ( x , y ) ⋅ d r \begin{aligned}
\int_{\widehat{AB}} \bm{F}(x, y) \boldsymbol{\cdot} \d \bm{r} &= -\int_{\widehat{BA}} \bm{F}(x, y) \boldsymbol{\cdot} \d \bm{r} \\
\int_C \bm{F}(x, y) \boldsymbol{\cdot} \d \bm{r} &= -\int_{-C} \bm{F}(x, y) \boldsymbol{\cdot} \d \bm{r}
\end{aligned}
∫ A B F ( x , y ) ⋅ d r ∫ C F ( x , y ) ⋅ d r = − ∫ B A F ( x , y ) ⋅ d r = − ∫ − C F ( x , y ) ⋅ d r
其中 − C -C − C C C C
理解成做功即可。
计算
设 F ( x , y ) = P ( x , y ) i + Q ( x , y ) j \bm{F}(x, y) = P(x, y) \bm{i} + Q(x, y) \bm{j} F ( x , y ) = P ( x , y ) i + Q ( x , y ) j C C C
设 C C C r ( t ) = ( φ ( t ) , ψ ( t ) ) \bm{r}(t) = \bigl(\varphi(t), \psi(t)\bigr) r ( t ) = ( φ ( t ) , ψ ( t ) ) t t t a a a b b b M ( x , y ) M(x, y) M ( x , y ) C C C A A A C C C B B B φ ( t ) , ψ ( t ) \varphi(t),\, \psi(t) φ ( t ) , ψ ( t ) [ a , b ] [a, b] [ a , b ] [ φ ′ ( t ) ] 2 + [ ψ ′ ( t ) ] 2 ≠ 0 [\varphi'(t)]^2 + [\psi'(t)]^2 \neq 0 [ φ ′ ( t ) ] 2 + [ ψ ′ ( t ) ] 2 = 0 第二类曲线积分 ∫ C P ( x , y ) d x + Q ( x , y ) d y \displaystyle\int_C P(x, y) \d x + Q(x, y) \d y ∫ C P ( x , y ) d x + Q ( x , y ) d y ,且
∫ C P ( x , y ) d x + Q ( x , y ) d y = ∫ a b [ P ( φ ( t ) , ψ ( t ) ) φ ′ ( t ) + Q ( φ ( t ) , ψ ( t ) ) ψ ′ ( t ) ] d t \int_C P(x, y) \d x + Q(x, y) \d y = \boxed{\int_a^b \Bigl[P\bigl(\varphi(t), \psi(t)\bigr) \varphi'(t) + Q\bigl(\varphi(t), \psi(t)\bigr) \psi'(t)\Bigr] \d t}
∫ C P ( x , y ) d x + Q ( x , y ) d y = ∫ a b [ P ( φ ( t ) , ψ ( t ) ) φ ′ ( t ) + Q ( φ ( t ) , ψ ( t ) ) ψ ′ ( t ) ] d t
两类曲线积分的联系
设有向曲线 C C C A A A B B B C C C r ( t ) = ( φ ( t ) , ψ ( t ) ) \bm{r}(t) = \bigl(\varphi(t), \psi(t)\bigr) r ( t ) = ( φ ( t ) , ψ ( t ) ) a ⩽ t ⩽ b a \le t \le b a ⩽ t ⩽ b
{ x = φ ( t ) y = ψ ( t ) ( a ⩽ t ⩽ b ) \left\lbrace\begin{aligned}
x &= \varphi(t) \\
y &= \psi(t) \\
\end{aligned}\right. \quad (a \le t \le b)
{ x y = φ ( t ) = ψ ( t ) ( a ⩽ t ⩽ b )
从而有 ( φ ′ ( t ) , ψ ′ ( t ) ) \bigl(\varphi'(t), \psi'(t)\bigr) ( φ ′ ( t ) , ψ ′ ( t ) )
d r = ( d x , d y ) = ( φ ′ ( t ) d t , ψ ′ ( t ) d t ) = ( φ ′ ( t ) , ψ ′ ( t ) ) d t \begin{aligned}
\d \bm{r} &= (\d x, \d y)\\
&= \bigl(\varphi'(t) \d t, \psi'(t) \d t\bigr)\\
&= \bigl(\varphi'(t), \psi'(t)\bigr) \d t\\
\end{aligned}
d r = ( d x , d y ) = ( φ ′ ( t ) d t , ψ ′ ( t ) d t ) = ( φ ′ ( t ) , ψ ′ ( t ) ) d t
也是 C C C
∣ d r ∣ = ( d x ) 2 + ( d y ) 2 = d s \left\lvert \d \bm{r} \right\rvert = \sqrt{(\d x)^2 + (\d y)^2} = \d s
∣ d r ∣ = ( d x ) 2 + ( d y ) 2 = d s
设 d r \d \bm{r} d r cos α , cos β \cos \alpha, \cos \beta cos α , cos β
( cos α , cos β ) = d r ∣ d r ∣ = ( d x d s , d y d s ) (\cos \alpha, \cos \beta) = \dfrac{\d \bm{r}}{\left\lvert \d \bm{r} \right\rvert} = \left(\dfrac{\d x}{\d s}, \dfrac{\d y}{\d s}\right)
( cos α , cos β ) = ∣ d r ∣ d r = ( d s d x , d s d y )
则
{ d x = cos α d s d y = cos β d s \left\lbrace\begin{aligned}
\d x &= \cos \alpha \d s\\
\d y &= \cos \beta \d s
\end{aligned}\right.
{ d x d y = cos α d s = cos β d s
因此
∫ C P d x + Q d y = ∫ C ( P cos α + Q cos β ) d s \boxed{
\int_C P \d x + Q \d y = \int_C (P \cos \alpha + Q \cos \beta) \d s
}
∫ C P d x + Q d y = ∫ C ( P cos α + Q cos β ) d s
其中 ( cos α , cos β ) (\cos \alpha, \cos \beta) ( cos α , cos β ) C C C ( x , y ) (x, y) ( x , y )
类似地,空间曲线上的两类曲线积分也有类似的联系:
∫ C P d x + Q d y + R d z = ∫ C ( P cos α + Q cos β + R cos γ ) d s \boxed{
\int_C P \d x + Q \d y + R \d z = \int_C (P \cos \alpha + Q \cos \beta + R \cos \gamma) \d s
}
∫ C P d x + Q d y + R d z = ∫ C ( P cos α + Q cos β + R cos γ ) d s
反过来,有
∫ C f ( x , y ) d s = ∫ C f ( x , y ) ⋅ ∣ d r ∣ = ∫ C f ( x , y ) d r ∣ d r ∣ ⋅ d r = ∫ C f ( x , y ) ( cos α , cos β ) ⋅ d r = ∫ C f ( x , y ) cos α d x + f ( x , y ) cos β d y \begin{aligned}
\int_C f(x, y) \d s &= \int_C f(x, y) \cdot \left\lvert\d \bm{r} \right\rvert \\
&= \int_C f(x, y) \dfrac{\d \bm{r}}{\left\lvert \d \bm{r} \right\rvert} \boldsymbol{\cdot} \d \bm{r}\\
&= \int_C f(x, y) (\cos \alpha, \cos \beta) \boldsymbol{\cdot} \d \bm{r}\\
&= \int_C f(x, y) \cos \alpha \d x + f(x, y) \cos \beta \d y\\
\end{aligned}
∫ C f ( x , y ) d s = ∫ C f ( x , y ) ⋅ ∣ d r ∣ = ∫ C f ( x , y ) ∣ d r ∣ d r ⋅ d r = ∫ C f ( x , y ) ( cos α , cos β ) ⋅ d r = ∫ C f ( x , y ) cos α d x + f ( x , y ) cos β d y
对于特殊的第一类曲线积分 ∫ C ∂ f ∂ n d s \displaystyle \int_C \dfrac{\partial f}{\partial \bm{n}} \d s ∫ C ∂ n ∂ f d s
∫ C ∂ f ∂ n d s = ∫ C ∇ f ⋅ n d s = ∫ C ( ∂ f ∂ x , ∂ f ∂ y ) ⋅ ( − cos β , cos α ) d s = ∫ C ( ∂ f ∂ y cos α − ∂ f ∂ x cos β ) d s = ∫ C ( ∂ f ∂ y , − ∂ f ∂ x ) ⋅ d r \begin{aligned}
\int_C \dfrac{\partial f}{\partial \bm{n}} \d s &= \int_C \grad f \boldsymbol{\cdot} \bm{n} \d s\\
&= \int_C \left( \dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y} \right) \boldsymbol{\cdot} \left( - \cos \beta, \cos \alpha \right) \d s\\
&= \int_C \left( \dfrac{\partial f}{\partial y} \cos \alpha - \dfrac{\partial f}{\partial x} \cos \beta \right) \d s\\
&= \int_C \left( \dfrac{\partial f}{\partial y}, - \dfrac{\partial f}{\partial x} \right) \boldsymbol{\cdot} \d \bm{r}
\end{aligned}
∫ C ∂ n ∂ f d s = ∫ C ∇ f ⋅ n d s = ∫ C ( ∂ x ∂ f , ∂ y ∂ f ) ⋅ ( − cos β , cos α ) d s = ∫ C ( ∂ y ∂ f cos α − ∂ x ∂ f cos β ) d s = ∫ C ( ∂ y ∂ f , − ∂ x ∂ f ) ⋅ d r
抄错笔记
上面的公式一开始我写的是下面的内容,但是复习时第二个等号那里我却实在是看不明白,盯了很长时间也搞不懂,也没查到相关资料,有点怀疑是自己抄错了。于是发邮件请教助教、老师,证实了是抄错了,估计是跟上面离得比较近,而我当时神智比较不清晰,当成连起来的就合并到一个 align 环境了,事后也没及时重温笔记。
( cos α , cos β ) (\cos \alpha, \cos \beta) ( cos α , cos β ) C C C n \bm{n} n
∫ C f ( x , y ) d s = ∫ C f ( x , y ) cos α d x + f ( x , y ) cos β d y = ∫ C ∂ f ∂ n d s = ∫ C ∇ f ⋅ n d s = ∫ C ( ∂ f ∂ x , ∂ f ∂ y ) ⋅ ( − cos β , cos α ) d s = ∫ C cos α ∂ f ∂ y − cos β ∂ f ∂ x d s \begin{aligned}
\int_C f(x, y) \d s &= \int_C f(x, y) \cos \alpha \d x + f(x, y) \cos \beta \d y\\
&= \int_C \dfrac{\partial f}{\partial \bm{n}} \d s\\
&= \int_C \grad f \boldsymbol{\cdot} \bm{n} \d s\\
&= \int_C \left(\dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y}\right) \boldsymbol{\cdot} (- \cos \beta, \cos \alpha) \d s\\
&= \int_C \cos \alpha \dfrac{\partial f}{\partial y} - \cos \beta \dfrac{\partial f}{\partial x} \d s
\end{aligned}
∫ C f ( x , y ) d s = ∫ C f ( x , y ) cos α d x + f ( x , y ) cos β d y = ∫ C ∂ n ∂ f d s = ∫ C ∇ f ⋅ n d s = ∫ C ( ∂ x ∂ f , ∂ y ∂ f ) ⋅ ( − cos β , cos α ) d s = ∫ C cos α ∂ y ∂ f − cos β ∂ x ∂ f d s
格林公式
设曲线 C C C
{ x = φ ( t ) y = ψ ( t ) ( a ⩽ t ⩽ b ) \left\lbrace\begin{aligned}
x &= \varphi(t)\\
y &= \psi(t)
\end{aligned}\right. \quad (a \le t \le b)
{ x y = φ ( t ) = ψ ( t ) ( a ⩽ t ⩽ b )
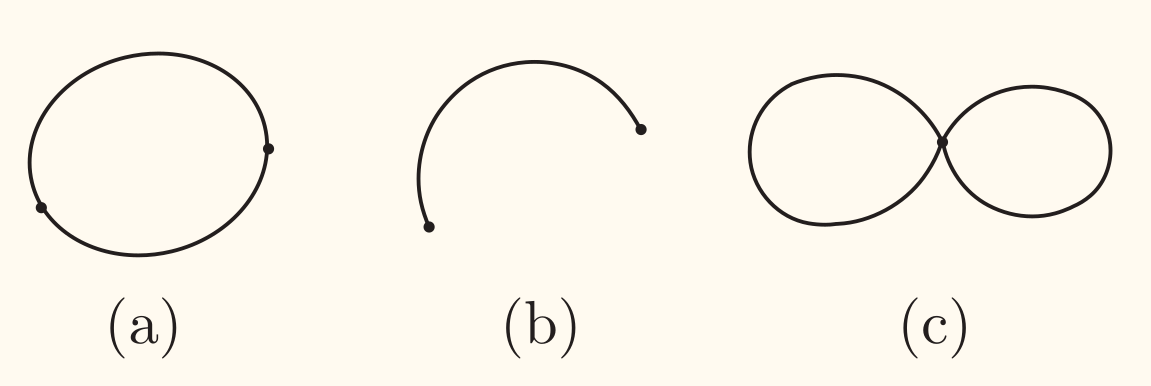
若 φ , ψ \varphi, \psi φ , ψ t 1 , t 2 ∈ [ a , b ] t_1, t_2 \in [a, b] t 1 , t 2 ∈ [ a , b ] t 1 < t 2 t_1 < t_2 t 1 < t 2 ( φ ( t 1 ) , ψ ( t 1 ) ) = ( φ ( t 2 ) , ψ ( t 2 ) ) \bigl(\varphi(t_1), \psi(t_1)\bigr) = \bigl(\varphi(t_2), \psi(t_2)\bigr) ( φ ( t 1 ) , ψ ( t 1 ) ) = ( φ ( t 2 ) , ψ ( t 2 ) ) t 1 = a , t 2 = b t_1 = a, t_2 = b t 1 = a , t 2 = b C C C 简单闭曲线 。
如下图,(a) \text{(a)} (a) (b), (c) \text{(b), (c)} (b), (c)
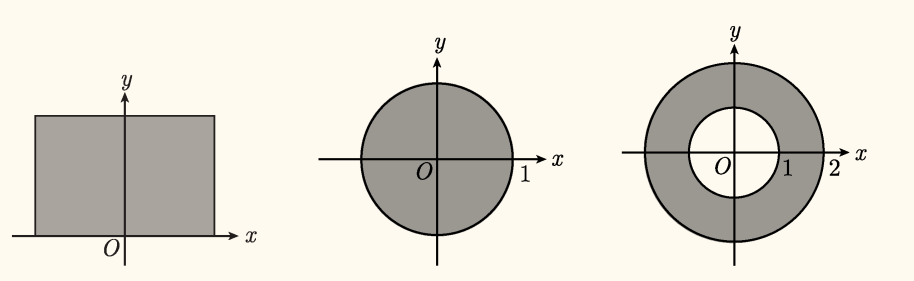
设 D D D D D D D D D D D D 单连通区域 ,否则称为多连通区域 。
如下图,第一、二个区域是单连通区域,第三个区域是多连通区域。
对于平面区域 D D D C C C C C C C C C D D D D D D 左侧 。
格林公式(Green Formula)
设有界闭区域 D D D ∂ D \partial D ∂ D P ( x , y ) P(x, y) P ( x , y ) Q ( x , y ) Q(x, y) Q ( x , y ) D D D
∮ ∂ D P d x + Q d y = ∬ D ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y \oint_{\partial D} P \d x + Q \d y = \iint_D \left(\dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y}\right) \d x \d y
∮ ∂ D P d x + Q d y = ∬ D ( ∂ x ∂ Q − ∂ y ∂ P ) d x d y
其中 ∂ D \partial D ∂ D D D D
证明
先证 ∮ ∂ D P d x = − ∬ D ∂ P ∂ y d x d y \displaystyle \oint_{\partial D} P \d x = - \iint_D \dfrac{\partial P}{\partial y}\d x \d y ∮ ∂ D P d x = − ∬ D ∂ y ∂ P d x d y
记 D D D { a ⩽ x ⩽ b , φ ( x ) ⩽ y ⩽ ψ ( x ) } \left\lbrace a \le x \le b, \varphi(x) \le y \le \psi(x) \right\rbrace { a ⩽ x ⩽ b , φ ( x ) ⩽ y ⩽ ψ ( x ) }
∬ D ( − ∂ P ∂ y ) d x d y = ∫ a b d x ∫ φ ( x ) ψ ( x ) ( − ∂ P ∂ y ) d y = ∫ a b − [ P ( x , ψ ( x ) ) − P ( x , φ ( x ) ) ] d x = ∫ a b P ( x , φ ( x ) ) d x + ∫ b a P ( x , ψ ( x ) ) d x = ∮ ∂ D P d x \begin{aligned}
\iint_D \left(- \dfrac{\partial P}{\partial y}\right)\d x \d y &= \int_a^b \d x \int_{\varphi(x)}^{\psi(x)} \left(- \dfrac{\partial P}{\partial y}\right) \d y\\
&= \int_a^b -\left[P\bigl(x, \psi(x)\bigr) - P\bigl(x, \varphi(x)\bigr)\right] \d x\\
&= \int_a^b P(x, \varphi(x)) \d x + \int_b^a P(x, \psi(x)) \d x\\
&= \oint_{\partial D} P \d x
\end{aligned}
∬ D ( − ∂ y ∂ P ) d x d y = ∫ a b d x ∫ φ ( x ) ψ ( x ) ( − ∂ y ∂ P ) d y = ∫ a b − [ P ( x , ψ ( x ) ) − P ( x , φ ( x ) ) ] d x = ∫ a b P ( x , φ ( x )) d x + ∫ b a P ( x , ψ ( x )) d x = ∮ ∂ D P d x
单连通、多连通区域可通过引入辅助线(辅助线上曲线积分方向相反,曲线积分抵消)将其化为上面的情形,可推知对所有情况成立。
同理可证 ∮ ∂ D Q d y = ∬ D ∂ Q ∂ x d x d y \displaystyle \oint_{\partial D} Q \d y = \iint_D \dfrac{\partial Q}{\partial x}\d x \d y ∮ ∂ D Q d y = ∬ D ∂ x ∂ Q d x d y
记 D D D { c ⩽ y ⩽ d , α ( y ) ⩽ x ⩽ β ( y ) } \left\lbrace c \le y \le d, \alpha(y) \le x \le \beta(y) \right\rbrace { c ⩽ y ⩽ d , α ( y ) ⩽ x ⩽ β ( y ) }
∮ ∂ D Q d y = ∫ c d Q ( β ( y ) , y ) d y + ∫ d c Q ( α ( y ) , y ) d y = ∫ c d ( Q ( β ( y ) , y ) − Q ( α ( y ) , y ) ) d y = ∫ c d d y ∫ α ( y ) β ( y ) ∂ Q ∂ x d x = ∬ D ∂ Q ∂ x d x d y \begin{aligned}
\oint_{\partial D} Q \d y &= \int_c^d Q\bigl(\beta(y), y\bigr) \d y + \int_d^c Q\bigl(\alpha(y), y\bigr) \d y\\
&= \int_c^d \Bigl(Q\bigl(\beta(y), y\bigr) - Q(\alpha(y), y)\Bigr) \d y\\
&= \int_c^d \d y \int_{\alpha(y)}^{\beta(y)} \dfrac{\partial Q}{\partial x} \d x\\
&= \iint_D \dfrac{\partial Q}{\partial x}\d x \d y
\end{aligned}
∮ ∂ D Q d y = ∫ c d Q ( β ( y ) , y ) d y + ∫ d c Q ( α ( y ) , y ) d y = ∫ c d ( Q ( β ( y ) , y ) − Q ( α ( y ) , y ) ) d y = ∫ c d d y ∫ α ( y ) β ( y ) ∂ x ∂ Q d x = ∬ D ∂ x ∂ Q d x d y
记忆(也可以当成是不太严谨的证明):
d ( P d x + Q d y ) = ( ∂ P ∂ x d x + ∂ P ∂ y d y ) d x + P d d x d x + ( ∂ Q ∂ x d x + ∂ Q ∂ y d y ) d y + Q d d y d y = ∂ P ∂ x d x 2 + ∂ P ∂ y d y d x + ∂ Q ∂ x d x d y + ∂ Q ∂ y d y 2 = − ∂ P ∂ y d x d y + ∂ Q ∂ x d x d y = ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y \begin{aligned}
\d \left( P \d x + Q \d y \right) &= \left( \dfrac{\partial P}{\partial x}\d x + \dfrac{\partial P}{\partial y}\d y \right) \d x + P \dfrac{\d }{\d x}\d x + \left( \dfrac{\partial Q}{\partial x}\d x + \dfrac{\partial Q}{\partial y}\d y \right) \d y + Q \dfrac{\d }{\d y}\d y\\
&= \dfrac{\partial P}{\partial x}\d x^2 + \dfrac{\partial P}{\partial y}\d y \d x + \dfrac{\partial Q}{\partial x}\d x \d y + \dfrac{\partial Q}{\partial y}\d y^2\\
&= - \dfrac{\partial P}{\partial y}\d x \d y + \dfrac{\partial Q}{\partial x}\d x \d y\\
&= \left( \dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \right) \d x \d y
\end{aligned}
d ( P d x + Q d y ) = ( ∂ x ∂ P d x + ∂ y ∂ P d y ) d x + P d x d d x + ( ∂ x ∂ Q d x + ∂ y ∂ Q d y ) d y + Q d y d d y = ∂ x ∂ P d x 2 + ∂ y ∂ P d y d x + ∂ x ∂ Q d x d y + ∂ y ∂ Q d y 2 = − ∂ y ∂ P d x d y + ∂ x ∂ Q d x d y = ( ∂ x ∂ Q − ∂ y ∂ P ) d x d y
d x \d x d x x x x d d x d x = 0 \dfrac{\d }{\d x}\d x = 0 d x d d x = 0
d x 2 = d x × d x = 0 , d y d x = d y × d x = − d x × d y = − d x d y \d x^2 = \d x \boldsymbol{\times} \d x = 0,\, \d y \d x = \d y \boldsymbol{\times} \d x = - \d x \boldsymbol{\times} \d y = - \d x \d y d x 2 = d x × d x = 0 , d y d x = d y × d x = − d x × d y = − d x d y
特别地,取 P = − y , Q = x P = -y, Q = x P = − y , Q = x
∮ ∂ D x d y − y d x = 2 ∬ D d x d y \oint_{\partial D} x \d y - y \d x = 2\iint_D \d x \d y
∮ ∂ D x d y − y d x = 2 ∬ D d x d y
即(后面两个,例如第一个是取 Q = x Q = x Q = x ∂ P ∂ y = 0 \dfrac{\partial P}{\partial y} = 0 ∂ y ∂ P = 0 P = c P = c P = c
σ ( D ) = 1 2 ∮ ∂ D x d y − y d x = ∮ ∂ D x d y = ∮ ∂ D − y d x \begin{aligned}
\sigma(D) &= \dfrac{1}{2} \oint_{\partial D} x \d y - y \d x\\
&= \oint_{\partial D} x \d y\\
&= \oint_{\partial D} -y \d x
\end{aligned}
σ ( D ) = 2 1 ∮ ∂ D x d y − y d x = ∮ ∂ D x d y = ∮ ∂ D − y d x
根据上面的「记法」,还可写为
∫ ∂ Ω α = ∫ Ω d α \int_{\partial \Omega} \alpha = \int_{\Omega} \d \alpha
∫ ∂ Ω α = ∫ Ω d α
求曲线积分
∮ C − ( x + y ) d x + ( x − y ) d y x 2 + y 2 \oint_C \dfrac{-(x + y)\d x + (x - y)\d y}{x^2 + y^2}
∮ C x 2 + y 2 − ( x + y ) d x + ( x − y ) d y
其中 C C C
P = − ( x + y ) x 2 + y 2 , Q = x − y x 2 + y 2 P = \dfrac{-(x + y)}{x^2 + y^2},\, Q = \dfrac{x - y}{x^2 + y^2} P = x 2 + y 2 − ( x + y ) , Q = x 2 + y 2 x − y ( x , y ) ≠ ( 0 , 0 ) (x, y) \ne (0, 0) ( x , y ) = ( 0 , 0 )
∂ Q ∂ x = ∂ P ∂ y = − x 2 + 2 x y + y 2 ( x 2 + y 2 ) 2 \dfrac{\partial Q}{\partial x} = \dfrac{\partial P}{\partial y} = \dfrac{-x^2 + 2xy + y^2}{(x^2 + y^2)^2}
∂ x ∂ Q = ∂ y ∂ P = ( x 2 + y 2 ) 2 − x 2 + 2 x y + y 2
因此对于 C C C D D D
若 D D D
∮ C P d x + Q d y = ∬ D ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y = ∬ D 0 d x d y = 0 \begin{aligned}
\oint_C P \d x + Q \d y &= \iint_D \left(\dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y}\right) \d x \d y\\
&= \iint_D 0 \d x \d y\\
&= 0
\end{aligned}
∮ C P d x + Q d y = ∬ D ( ∂ x ∂ Q − ∂ y ∂ P ) d x d y = ∬ D 0 d x d y = 0
若 D D D r > 0 r > 0 r > 0 l : x 2 + y 2 = r 2 l\colon x^2 + y^2 = r^2 l : x 2 + y 2 = r 2 D D D C C C l l l D 1 D_1 D 1 ∂ D 1 = C + l − \partial D_1 = C + l^{-} ∂ D 1 = C + l − D 1 D_1 D 1
∮ C + l − P d x + Q d y = ∬ D 1 0 d x d y = 0 \begin{aligned}
\oint_{C + l^{-}} P \d x + Q \d y &= \iint_{D_1} 0 \d x \d y\\
&= 0
\end{aligned}
∮ C + l − P d x + Q d y = ∬ D 1 0 d x d y = 0
因此
∮ C P d x + Q d y = ∮ C + l − ( P d x + Q d y ) + ∮ l ( P d x + Q d y ) = 0 + ∮ l P d x + Q d y = ∫ 0 2 π − ( r cos θ + r sin θ ) ( − r sin θ ) + ( r cos θ − r sin θ ) ( r cos θ ) r 2 d θ = ∫ 0 2 π d θ = 2 π \begin{aligned}
\oint_C P \d x + Q \d y &= \oint_{C + l^{-}} (P \d x + Q \d y) + \oint_{l} (P \d x + Q \d y)\\
&= 0 + \oint_{l} P \d x + Q \d y\\
&= \int_0^{2 \pi} \dfrac{-(r \cos \theta + r \sin \theta)(-r \sin \theta) + (r \cos \theta - r \sin \theta)(r \cos \theta)}{r^2} \d \theta\\
&= \int_0^{2 \pi} \d \theta\\
&= 2 \pi
\end{aligned}
∮ C P d x + Q d y = ∮ C + l − ( P d x + Q d y ) + ∮ l ( P d x + Q d y ) = 0 + ∮ l P d x + Q d y = ∫ 0 2 π r 2 − ( r cos θ + r sin θ ) ( − r sin θ ) + ( r cos θ − r sin θ ) ( r cos θ ) d θ = ∫ 0 2 π d θ = 2 π
这题旨在说明奇点可能会影响格林公式对曲线积分的应用,因此需要分类讨论。
设曲线 Γ \Gamma Γ D : { ( x , y ) ∣ 0 ⩽ x ⩽ π , 0 ⩽ y ⩽ sin x } D\colon \left\lbrace (x, y) \mid 0 \le x \le \pi, 0 \le y \le \sin x\right\rbrace D : { ( x , y ) ∣ 0 ⩽ x ⩽ π , 0 ⩽ y ⩽ sin x } n \bm{n} n Γ \Gamma Γ
∫ Γ ∂ f ∂ n d s \int_{\Gamma} \dfrac{\partial f}{\partial \bm{n}}\d s
∫ Γ ∂ n ∂ f d s
设切向量 t = ( cos α , cos β ) \bm{t} = \left(\cos \alpha, \cos \beta\right) t = ( cos α , cos β ) n = ( cos β , − cos α ) \bm{n} = \left(\cos \beta, -\cos \alpha\right) n = ( cos β , − cos α ) π 2 \dfrac{\pi}{2} 2 π
∫ Γ ∂ f ∂ n d s = ∫ Γ ∇ f ⋅ n d s = ∫ Γ ( ∂ f ∂ x cos β − ∂ f ∂ y cos α ) d s = ∫ Γ − ∂ f ∂ y d x + ∂ f ∂ x d y = ∬ D ( ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 ) d x d y = ∬ Δ f d x d y \begin{aligned}
\int_{\Gamma}\dfrac{\partial f}{\partial \bm{n}}\d s &= \int_{\Gamma} \grad f \boldsymbol{\cdot} \bm{n} \d s\\
&= \int_{\Gamma} \left( \dfrac{\partial f}{\partial x}\cos \beta - \dfrac{\partial f}{\partial y} \cos \alpha \right) \d s\\
&= \int_{\Gamma} -\dfrac{\partial f}{\partial y}\d x + \dfrac{\partial f}{\partial x} \d y\\
&= \iint_D \left( \dfrac{\partial^2 f}{\partial x^2} + \dfrac{\partial^2 f}{\partial y^2} \right) \d x \d y\\
&= \iint \Delta f \d x \d y\\
\end{aligned}
∫ Γ ∂ n ∂ f d s = ∫ Γ ∇ f ⋅ n d s = ∫ Γ ( ∂ x ∂ f cos β − ∂ y ∂ f cos α ) d s = ∫ Γ − ∂ y ∂ f d x + ∂ x ∂ f d y = ∬ D ( ∂ x 2 ∂ 2 f + ∂ y 2 ∂ 2 f ) d x d y = ∬ Δ f d x d y
其中 Δ = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 \Delta = \dfrac{\partial^2}{\partial x^2} + \dfrac{\partial^2}{\partial y^2} Δ = ∂ x 2 ∂ 2 + ∂ y 2 ∂ 2 拉普拉斯算子 。即 Δ = ∇ 2 = ∇ ⋅ ∇ = ∇ ⊺ ∇ \Delta = \grad^2 = \grad \boldsymbol{\cdot} \grad = \grad^\intercal \grad Δ = ∇ 2 = ∇ ⋅ ∇ = ∇ ⊺ ∇
另外可以注意到,∇ ∇ ⊺ = H \grad \grad^\intercal = \bm{H} ∇ ∇ ⊺ = H
虽然常记 ∇ = ( ∂ ∂ x , ∂ ∂ y ) \grad = \left( \dfrac{\partial }{\partial x}, \dfrac{\partial }{\partial y} \right) ∇ = ( ∂ x ∂ , ∂ y ∂ ) ∇ = [ ∂ ∂ x ∂ ∂ y ] \grad = \begin{bmatrix} \dfrac{\partial }{\partial x} \\ \dfrac{\partial }{\partial y} \end{bmatrix} ∇ = ∂ x ∂ ∂ y ∂ 2 × 1 2 \times 1 2 × 1 1 × 2 1 \times 2 1 × 2
平面上第二类曲线积分与路径无关的条件
设 G G G P ( x , y ) , Q ( x , y ) P(x, y), Q(x, y) P ( x , y ) , Q ( x , y ) G G G G G G A , B A, B A , B G G G A A A B B B L 1 , L 2 L_{1}, L_{2} L 1 , L 2
∫ L 1 P d x + Q d y = ∫ L 2 P d x + Q d y \int_{L_{1}} P \d x + Q \d y = \int_{L_{2}} P \d x + Q \d y
∫ L 1 P d x + Q d y = ∫ L 2 P d x + Q d y
则称曲线积分 ∫ L P d x + Q d y \displaystyle \int_{L} P \d x + Q \d y ∫ L P d x + Q d y G G G 与路径无关 。否则就称与路径有关 。
其等价于 G G G L L L
∮ L P d x + Q d y = 0 \oint_{L} P \d x + Q \d y = 0
∮ L P d x + Q d y = 0
因为有
∮ L 1 − L 2 P d x + Q d y = 0 \oint_{L_1 - L_2} P \d x + Q \d y = 0
∮ L 1 − L 2 P d x + Q d y = 0
则由格林公式有
设 D D D 单连通区域 ,函数 P ( x , y ) , Q ( x , y ) P(x, y), Q(x, y) P ( x , y ) , Q ( x , y ) D D D 有一阶连续 偏导数 ,则曲线积分 ∫ C P d x + Q d y \displaystyle \int_{C} P \d x+Q \d y ∫ C P d x + Q d y D D D 充分必要条件 是
∂ Q ∂ x = ∂ P ∂ y \dfrac{\partial Q}{\partial x} = \dfrac{\partial P}{\partial y}
∂ x ∂ Q = ∂ y ∂ P
在 D D D
充分性由格林公式显然证得。
必要性采用反证法,不妨设 ∃ ( x 0 , y 0 ) \exists (x_0, y_0) ∃ ( x 0 , y 0 ) ∂ Q ∂ x − ∂ P ∂ y ∣ ( x 0 , y 0 ) = η > 0 \dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \as_{(x_0, y_0)} = \eta > 0 ∂ x ∂ Q − ∂ y ∂ P ( x 0 , y 0 ) = η > 0
由连续性知,存在 δ > 0 \delta > 0 δ > 0 ( x 0 , y 0 ) (x_0, y_0) ( x 0 , y 0 ) δ \delta δ ∂ Q ∂ x − ∂ P ∂ y ⩾ 1 2 η > 0 \dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \ge \dfrac{1}{2} \eta > 0 ∂ x ∂ Q − ∂ y ∂ P ⩾ 2 1 η > 0
设 γ \gamma γ ( x 0 , y 0 ) (x_0, y_0) ( x 0 , y 0 ) δ \delta δ
∮ ∂ γ P d x + Q d y = ∬ γ ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y ⩾ ∬ γ 1 2 η d x d y = 1 2 η π δ 2 > 0 \begin{aligned}
\oint_{\partial \gamma} P \d x + Q \d y &= \iint_{\gamma} \left( \dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \right) \d x \d y\\
&\ge \iint_{\gamma} \dfrac{1}{2} \eta \d x \d y\\
&= \dfrac{1}{2} \eta \pi \delta^2 > 0
\end{aligned}
∮ ∂ γ P d x + Q d y = ∬ γ ( ∂ x ∂ Q − ∂ y ∂ P ) d x d y ⩾ ∬ γ 2 1 η d x d y = 2 1 η π δ 2 > 0
与沿 D D D
需要强调的是,「单连通区域」与「一阶连续偏导数」是必要的条件,否则上面的定理不可用。
假如非单连通区域,例如上面的 P = − ( x + y ) x 2 + y 2 , Q = x − y x 2 + y 2 P = \dfrac{-(x + y)}{x^2 + y^2},\, Q = \dfrac{x - y}{x^2 + y^2} P = x 2 + y 2 − ( x + y ) , Q = x 2 + y 2 x − y D = { ( x , y ) ∣ 1 ⩽ x 2 + y 2 ⩽ 2 } D=\left\{(x, y) \mid 1 \le x^{2}+y^{2} \le 2\right\} D = { ( x , y ) ∣ 1 ⩽ x 2 + y 2 ⩽ 2 } ∂ Q ∂ x = ∂ P ∂ y \dfrac{\partial Q}{\partial x} = \dfrac{\partial P}{\partial y} ∂ x ∂ Q = ∂ y ∂ P D D D C C C ∮ C P d x + Q d y = 2 π ≠ 0 \displaystyle \oint_{C} P \d x + Q \d y = 2 \pi \ne 0 ∮ C P d x + Q d y = 2 π = 0
曲线积分与路径无关时,常将从起点 A A A B B B
∫ A B P d x + Q d y \int_{A}^{B} P \d x + Q \d y
∫ A B P d x + Q d y
设 D D D 单连通区域 ,函数 P ( x , y ) , Q ( x , y ) P(x, y), Q(x, y) P ( x , y ) , Q ( x , y ) D D D 具有一阶连续 偏导数 ,则 P ( x , y ) d x + Q ( x , y ) d y P(x, y) \d x+Q(x, y) \d y P ( x , y ) d x + Q ( x , y ) d y D D D u ( x , y ) u(x, y) u ( x , y ) 充分必要条件 是
∂ Q ∂ x = ∂ P ∂ y \dfrac{\partial Q}{\partial x} = \dfrac{\partial P}{\partial y}
∂ x ∂ Q = ∂ y ∂ P
在 D D D
必要性。设 P d x + Q d y P \d x + Q \d y P d x + Q d y u u u
P d x + Q d y = d u P \d x + Q \d y = \d u
P d x + Q d y = d u
从而
{ P = ∂ u ∂ x Q = ∂ u ∂ y \left\lbrace\begin{aligned}
P &= \dfrac{\partial u}{\partial x}\\
Q &= \dfrac{\partial u}{\partial y}
\end{aligned}\right.
⎩ ⎨ ⎧ P Q = ∂ x ∂ u = ∂ y ∂ u
则
{ ∂ P ∂ y = ∂ 2 u ∂ y ∂ x ∂ Q ∂ x = ∂ 2 u ∂ x ∂ y \left\lbrace\begin{aligned}
\dfrac{\partial P}{\partial y} &= \dfrac{\partial^2 u}{\partial y \partial x}\\
\dfrac{\partial Q}{\partial x} &= \dfrac{\partial^2 u}{\partial x \partial y}
\end{aligned}\right.
⎩ ⎨ ⎧ ∂ y ∂ P ∂ x ∂ Q = ∂ y ∂ x ∂ 2 u = ∂ x ∂ y ∂ 2 u
因为 P , Q P, Q P , Q u u u ∂ 2 u ∂ x ∂ y = ∂ 2 u ∂ y ∂ x \dfrac{\partial^2 u}{\partial x \partial y} = \dfrac{\partial^2 u}{\partial y \partial x} ∂ x ∂ y ∂ 2 u = ∂ y ∂ x ∂ 2 u
∂ Q ∂ x = ∂ P ∂ y \dfrac{\partial Q}{\partial x} = \dfrac{\partial P}{\partial y}
∂ x ∂ Q = ∂ y ∂ P
充分性。由上面的定理知曲线积分
∫ A B P d x + Q d y \int_{A}^{B} P \d x + Q \d y
∫ A B P d x + Q d y
与路径无关,固定起点 A ( x 0 , y 0 ) A(x_0, y_0) A ( x 0 , y 0 ) B ( x , y ) B(x, y) B ( x , y ) D D D ( x , y ) (x, y) ( x , y ) u ( x , y ) u(x, y) u ( x , y )
u ( x , y ) = ∫ ( x 0 , y 0 ) ( x , y ) P d x + Q d y u(x, y) = \int_{(x_0, y_0)}^{(x, y)} P \d x + Q \d y
u ( x , y ) = ∫ ( x 0 , y 0 ) ( x , y ) P d x + Q d y
下证 P d x + Q d y P \d x + Q \d y P d x + Q d y u ( x , y ) u(x, y) u ( x , y )
只需证
{ ∂ u ∂ x = P ∂ u ∂ y = Q \left\lbrace\begin{aligned}
\dfrac{\partial u}{\partial x} &= P\\
\dfrac{\partial u}{\partial y} &= Q
\end{aligned}\right.
⎩ ⎨ ⎧ ∂ x ∂ u ∂ y ∂ u = P = Q
对于任意的定点 B ( x , y ) B(x, y) B ( x , y ) ∣ Δ x ∣ |\Delta x| ∣Δ x ∣ B ′ ( x + Δ x , y ) B^{\prime}(x+\Delta x, y) B ′ ( x + Δ x , y ) B B ′ B B^{\prime} B B ′ D D D
有
∂ u ∂ x = lim Δ x → 0 u ( x + Δ x , y ) − u ( x , y ) Δ x = lim Δ x → 0 ∫ ( x 0 , y 0 ) ( x + Δ x , y ) P d x + Q d y − ∫ ( x 0 , y 0 ) ( x , y ) P d x + Q d y Δ x = lim Δ x → 0 ∫ ( x , y ) ( x + Δ x , y ) P d x + Q d y Δ x = lim Δ x → 0 ∫ ( x , y ) ( x + Δ x , y ) P d x Δ x = P \begin{aligned}
\dfrac{\partial u}{\partial x} &= \lim\limits_{\Delta x \to 0} \dfrac{u(x + \Delta x, y) - u(x, y)}{\Delta x}\\
&= \lim\limits_{\Delta x \to 0} \dfrac{\displaystyle \int_{(x_0, y_0)}^{(x + \Delta x, y)} P \d x + Q \d y - \int_{(x_0, y_0)}^{(x, y)} P \d x + Q \d y}{\Delta x}\\
&= \lim\limits_{\Delta x \to 0} \dfrac{\displaystyle \int_{(x, y)}^{(x + \Delta x, y)} P \d x + Q \d y}{\Delta x}\\
&= \lim\limits_{\Delta x \to 0} \dfrac{\displaystyle \int_{(x, y)}^{(x + \Delta x, y)} P \d x}{\Delta x}\\
&= P
\end{aligned}
∂ x ∂ u = Δ x → 0 lim Δ x u ( x + Δ x , y ) − u ( x , y ) = Δ x → 0 lim Δ x ∫ ( x 0 , y 0 ) ( x + Δ x , y ) P d x + Q d y − ∫ ( x 0 , y 0 ) ( x , y ) P d x + Q d y = Δ x → 0 lim Δ x ∫ ( x , y ) ( x + Δ x , y ) P d x + Q d y = Δ x → 0 lim Δ x ∫ ( x , y ) ( x + Δ x , y ) P d x = P
同理可证 ∂ u ∂ y = Q \dfrac{\partial u}{\partial y} = Q ∂ y ∂ u = Q
设区域 D D D 单连通区域 ,函数 P ( x , y ) , Q ( x , y ) P(x, y), Q(x, y) P ( x , y ) , Q ( x , y ) D D D 具有一阶连续 偏导数 ,对于 D D D A , B A, B A , B ∫ A B ^ P d x + Q d y \displaystyle \int_{\widehat{A B}} P\d x+Q\d y ∫ A B P d x + Q d y 充分必要条件 是:
P d x + Q d y P\d x+Q\d y P d x + Q d y u ( x , y ) u(x, y) u ( x , y ) d u = P d x + Q d y \d u=P\d x+Q\d y d u = P d x + Q d y P d x + Q d y P\d x+Q \d y P d x + Q d y 恰当微分 )。此时有
∫ A B ^ P d x + Q d y = ∫ A B d u = u ( B ) − u ( A ) \int_{\widehat{A B}} P \mathrm{~d} x+Q \mathrm{~d} y=\int_{A}^{B} \mathrm{~d} u=u(B)-u(A)
∫ A B P d x + Q d y = ∫ A B d u = u ( B ) − u ( A )
其中 u ( A ) , u ( B ) u(A), u(B) u ( A ) , u ( B ) u ( x , y ) u(x, y) u ( x , y ) A , B A, B A , B
很像啊,很像牛顿-莱布尼茨公式,因此称为曲线积分的基本公式 。
对于满足
d u = P d x + Q d y \d u = P \d x + Q \d y
d u = P d x + Q d y
的函数 u u u P d x + Q d y P \d x + Q \d y P d x + Q d y
由于路径无关,为了计算的简便,可以选取一些简单的曲线进行计算,如直线或平行于坐标轴的折线等。