各式各样的矩阵及矩阵运算

发表于 更新于 阅读次数： Waline： 本文字数： 3.7k 阅读时长 ≈ 13 分钟
《线性代数》笔记

笔记

分块矩阵

乘法

若 A=[A11A12⋯A1sA21A22⋯A2s⋮⋮⋱⋮Ar1Ar2⋯Ars]\bm{A} = \begin{bmatrix} \bm{A}_{11} & \bm{A}_{12} & \cdots & \bm{A}_{1s} \\ \bm{A}_{21} & \bm{A}_{22} & \cdots & \bm{A}_{2s} \\ \vdots & \vdots & \ddots & \vdots \\ \bm{A}_{r1} & \bm{A}_{r2} & \cdots & \bm{A}_{rs} \\ \end{bmatrix}，B=[B11B12⋯B1tB21B22⋯B2t⋮⋮⋱⋮Bs1Bs2⋯Bst]\bm{B} = \begin{bmatrix} \bm{B}_{11} & \bm{B}_{12} & \cdots & \bm{B}_{1t} \\ \bm{B}_{21} & \bm{B}_{22} & \cdots & \bm{B}_{2t} \\ \vdots & \vdots & \ddots & \vdots \\ \bm{B}_{s1} & \bm{B}_{s2} & \cdots & \bm{B}_{st} \\ \end{bmatrix}，则 C=AB=(Ckl)r×t\bm{C}=\bm{A}\bm{B}=(\bm{C}_{kl})_{r \times t}，其中

Ckl=Ak1B1l+Ak2B2l+⋯+AksBsl=∑i=1sAkiBil\bm{C}_{kl} = \bm{A}_{k1}\bm{B}_{1l} + \bm{A}_{k2}\bm{B}_{2l} + \cdots + \bm{A}_{ks}\bm{B}_{sl} = \sum_{i=1}^s \bm{A}_{ki}\bm{B}_{il}

若 A=[A11O⋯OA21A22⋯O⋮⋮⋱⋮An1An2⋯Ann]\bm{A} = \begin{bmatrix} \bm{A}_{11} & \bm{O} & \cdots & \bm{O} \\ \bm{A}_{21} & \bm{A}_{22} & \cdots & \bm{O} \\ \vdots & \vdots & \ddots & \vdots \\ \bm{A}_{n1} & \bm{A}_{n2} & \cdots & \bm{A}_{nn} \\ \end{bmatrix}，则

∣An×n∣=∣A11∣∣A22∣⋯∣Ann∣=∏i=1n∣Aii∣\left\lvert \bm{A}_{n \times n} \right\rvert = \left\lvert \bm{A}_{11} \right\rvert \left\lvert \bm{A}_{22} \right\rvert \cdots \left\lvert \bm{A}_{nn} \right\rvert = \prod_{i=1}^n \left\lvert \bm{A}_{ii} \right\rvert

证明：

对 A\bm{A} 进行变换得 A=[B11O⋯OB21B22⋯O⋮⋮⋱⋮Bn1Bn2⋯Bnn]\bm{A} = \begin{bmatrix} \bm{B}_{11} & \bm{O} & \cdots & \bm{O} \\ \bm{B}_{21} & \bm{B}_{22} & \cdots & \bm{O} \\ \vdots & \vdots & \ddots & \vdots \\ \bm{B}_{n1} & \bm{B}_{n2} & \cdots & \bm{B}_{nn} \\ \end{bmatrix}，其中 Bii\bm{B}_{ii} 为下三角矩阵。

则 ∣A∣=∣B11∣∣B22∣⋯∣Bnn∣\left\lvert \bm{A} \right\rvert = \left\lvert \bm{B}_{11} \right\rvert \left\lvert \bm{B}_{22} \right\rvert \cdots \left\lvert \bm{B}_{nn} \right\rvert，而 ∣Aij∣=∣Bij∣\left\lvert \bm{A}_{ij} \right\rvert = \left\lvert \bm{B}_{ij} \right\rvert，从而得证。

这里的变换可不是瞎变换。

具体而言，对对角线上某个矩阵 AiiA_{ii}，对其进行行变换和列变换，会分别带动 Ai1, ⋯ , Ai,i−1A_{i 1},\, \cdots ,\, A_{i, i-1} 和 Ai+1,i, ⋯ , AniA_{i + 1, i},\, \cdots ,\, A_{ni}（当然还有零矩阵，只不过变换对它们没有影响），只不过因为它们在三角形里面，所以没有影响。

转置

若 A=[A11A12⋯A1sA21A22⋯A2s⋮⋮⋱⋮Ar1Ar2⋯Ars]\bm{A} = \begin{bmatrix} \bm{A}_{11} & \bm{A}_{12} & \cdots & \bm{A}_{1s} \\ \bm{A}_{21} & \bm{A}_{22} & \cdots & \bm{A}_{2s} \\ \vdots & \vdots & \ddots & \vdots \\ \bm{A}_{r1} & \bm{A}_{r2} & \cdots & \bm{A}_{rs} \\ \end{bmatrix}，则 A⊺=[A11⊺A21⊺⋯Ar1⊺A12⊺A22⊺⋯Ar2⊺⋮⋮⋱⋮A1s⊺A2s⊺⋯Ars⊺]\bm{A}^{\intercal} = \begin{bmatrix} \bm{A}_{11}^{\intercal} & \bm{A}_{21}^{\intercal} & \cdots & \bm{A}_{r1}^{\intercal} \\ \bm{A}_{12}^{\intercal} & \bm{A}_{22}^{\intercal} & \cdots & \bm{A}_{r2}^{\intercal} \\ \vdots & \vdots & \ddots & \vdots \\ \bm{A}_{1s}^{\intercal} & \bm{A}_{2s}^{\intercal} & \cdots & \bm{A}_{rs}^{\intercal} \\ \end{bmatrix}。

初等变换

  1. 对调变换：交换矩阵的两行（列），记为 ri↔rjr_i \leftrightarrow r_j（ci↔cjc_i \leftrightarrow c_j）。
  2. 数乘变换：把矩阵的某一行（列）乘以一个非零常数 kk，记为 krik r_i（kcik c_i）。
  3. 倍加变换：把矩阵的某一行（列）的 kk 倍加到另一行（列）上，记为 ri+krjr_i + k r_j（ci+kcjc_i + k c_j）。

单位矩阵 E\bm{E} 经过一次初等变换得到的矩阵称为初等矩阵。

  1. 初等对调矩阵：E(i,j)\bm{E}(i, j)
  2. 初等倍乘矩阵：E(i(k))\bm{E}(i(k))
  3. 初等倍加矩阵：E(i,j(k))\bm{E}(i, j(k))

上面是「数乘」，这里又是「倍加」。。。

E(i,j(k))=[E(j,i(k))]⊺E(i, j(k)) = \left[ E(j, i(k)) \right]^\intercal

若矩阵 A\bm{A} 经过有限次初等变换得到矩阵 B\bm{B}，则称 A\bm{A} 和 B\bm{B} 等价，记为 A→B\bm{A} \to \bm{B}。

显然，A→B  ⟺  B→A\bm{A} \to \bm{B} \iff \bm{B} \to \bm{A}。

梯形矩阵

行梯形矩阵

  1. 若有零行，则零行在最下方。
  2. 从第一行起，每行第一个非零元素（主元）所在的列号逐行递增。

行简化梯形矩阵

  1. 为行梯形矩阵。
  2. 主元为 11，且主元所在列的其他元素都为 00。

同理可定义列梯形矩阵和列简化梯形矩阵。

标准形矩阵

既为行简化梯形矩阵，又为列简化梯形矩阵。

可记作

[EOOO]\begin{bmatrix} \bm{E} & \bm{O} \\ \bm{O} & \bm{O} \end{bmatrix}

可知，解线性方程组时，将系数矩阵变为增广矩阵，原系数矩阵变为上三角矩阵时，增广矩阵即为行梯形矩阵；原系数矩阵变为单位矩阵时，即为行简化梯形矩阵。

定理

  1. 对矩阵 A\bm{A} 进行有限次初等行变化，可以得到行简化梯形矩阵。
  2. 对矩阵 A\bm{A} 进行有限次初等列变化，可以得到列简化梯形矩阵。
  3. 对矩阵 A\bm{A} 进行有限次初等行变化和初等列变化，可以得到标准形矩阵。

伴随矩阵 & 逆矩阵

伴随矩阵

伴随矩阵

设 A=[aij]n\bm{A} = \left[ a_{ij} \right]_n 为 nn 阶方阵，AijA_{ij} 是 aija_{ij} 的代数余子式，则

A∗=[Aij]n⊺\bm{A}^* = \left[ A_{ij} \right]_n^\intercal

称为 A\bm{A} 的伴随矩阵。

易得

AA∗=A∗A=∣A∣E\bm{A} \bm{A}^* = \bm{A}^* \bm{A} = \left\lvert \bm{A} \right\rvert \bm{E}

由此，我们可知 A−1=A∗∣A∣\bm{A}^{-1}=\dfrac{\bm{A}^{*}}{\left\lvert A \right\rvert}（A\bm{A} 可逆时）。

∣A∗∣=∣A∣n−1\left\lvert \bm{A}^{*} \right\rvert = \left\lvert \bm{A} \right\rvert^{n-1}

证明：

∣A∗∣=∣∣A∣A−1∣=∣A∣n∣A∣−1=∣A∣n−1\begin{aligned} \left\lvert \bm{A}^{*} \right\rvert &= \left\lvert \left\lvert \bm{A} \right\rvert \bm{A}^{-1} \right\rvert \\ &= \left\lvert \bm{A} \right\rvert^n \left\lvert \bm{A} \right\rvert^{-1} \\ &= \left\lvert \bm{A} \right\rvert^{n-1} \end{aligned}

(AB)∗=B∗A∗\left( \bm{A} \bm{B} \right)^{*} = \bm{B}^{*} \bm{A}^{*}

逆矩阵

对 nn 阶方阵 A\bm{A}，若存在 nn 阶方阵 B\bm{B}，使 AB=BA=E\bm{A} \bm{B} = \bm{B} \bm{A} = \bm{E}，则称 A\bm{A} 为可逆矩阵，B\bm{B} 为 A\bm{A} 的逆矩阵，记为 A−1\bm{A}^{-1}。

证明一下若存在 AB=CA=E\bm{A} \bm{B} = \bm{C} \bm{A} = \bm{E}，则 B=C\bm{B} = \bm{C}。

AB=CA=E  ⟹  CAB=CE  ⟹  (CA)B=C  ⟹  EB=C  ⟹  B=C\begin{aligned} \bm{A} \bm{B} = \bm{C} \bm{A} = \bm{E} &\implies \bm{C} \bm{A} \bm{B} = \bm{C} \bm{E} \\ &\implies (\bm{C} \bm{A}) \bm{B} = \bm{C} \\ &\implies \bm{E} \bm{B} = \bm{C}\\ &\implies \bm{B} = \bm{C} \end{aligned}

逆矩阵的性质

以下均假设 A, B\bm{A},\, \bm{B} 可逆。

  1. (A−1)−1=A\left( \bm{A}^{-1} \right)^{-1} = \bm{A}
  2. ∣A−1∣=∣A∣−1\left\lvert \bm{A}^{-1} \right\rvert = \left\lvert \bm{A} \right\rvert^{-1}
  3. 若 k≠0k\ne 0，(kA)−1=k−1A−1\left( k \bm{A} \right)^{-1} = k^{-1} \bm{A}^{-1}
  4. (A⊺)−1=(A−1)⊺\left( \bm{A}^\intercal \right)^{-1} = \left( \bm{A}^{-1} \right)^\intercal
  5. (AB)−1=B−1A−1\left( \bm{A} \bm{B} \right)^{-1} = \bm{B}^{-1} \bm{A}^{-1}

初等矩阵的逆

  1. E−1(i,j)=E(i,j)\bm{E}^{-1}(i, j) = \bm{E}(i, j)
  2. E−1(i(k))=E(i(1k))\bm{E}^{-1}(i(k)) = \bm{E}(i(\frac{1}{k}))
  3. E−1(i,j(k))=E(i,j(−k))\bm{E}^{-1}(i, j(k)) = \bm{E}(i, j(-k))

从而有

[λ1λ2⋱λn]−1=[λ1−1λ2−1⋱λn−1][λ1λ2. . .λn]−1=[λn−1. . .λ2−1λ1−1]\newcommand\iddots{\mathinner{\kern{1.2mu}\raisebox{2mu}{.}\kern{3mu}\raisebox{7.4mu}{.}\kern{3mu}\raisebox{12.8mu}{.}\kern{1.2mu}}} \begin{aligned} \begin{bmatrix} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \ddots & \\ & & & \lambda_n \end{bmatrix}^{-1} &= \begin{bmatrix} \lambda_1^{-1} & & & \\ & \lambda_2^{-1} & & \\ & & \ddots & \\ & & & \lambda_n^{-1} \end{bmatrix} \\ \begin{bmatrix} & & & \lambda_1 \\ & & \lambda_2 & \\ & \iddots & & \\ \lambda_n & & & \end{bmatrix}^{-1} &= \begin{bmatrix} & & & \lambda_n^{-1} \\ & & \iddots & \\ & \lambda_2^{-1} & & \\ \lambda_1^{-1} & & & \end{bmatrix} \end{aligned}

对一般的 2×22 \times 2 矩阵，有

[abcd]−1=[d−b−ca]ad−bc=[d−b−ca]∣d−b−ca∣\begin{bmatrix} a & b \\ c & d \end{bmatrix}^{-1} = \dfrac{\begin{bmatrix} d & -b \\ -c & a \end{bmatrix}}{ad-bc} = \dfrac{\begin{bmatrix} d & -b \\ -c & a \end{bmatrix}}{\begin{vmatrix} d & -b \\ -c & a \end{vmatrix}}

KaTeX\KaTeX 不支持 \iddots，参考 StackExchange，稍加修改：

\newcommand\iddots{\mathinner{\kern{1.2mu}\raisebox{2mu}{.}\kern{3mu}\raisebox{7.4mu}{.}\kern{3mu}\raisebox{12.8mu}{.}\kern{1.2mu}}}

原本是稍加修改，最后不满意效果，自己又调间距调了一个小时。

想到高二时，调电子轨道表达式（是叫这个名字吧？）的 macro 的间距也是调了很久，最后没能弄出一个满意的效果，就勉强用着了。

前阵子还试过重新调，结果还是没能令我满意，而且缩放还会改效果。

这个矩阵的省略号，最后勉强算是和镜像重合了，见 issue 的图。调过程中发现矩阵两侧高度不同，不管是正常还是我调的，而且位置也会影响，着实闹心。

到此打住。

杂项

零幂矩阵

零幂矩阵

若 ∃k∈N, Jk=O\exist_{k \in \N},\, \bm{J}^k = \bm{O}，则称 J\bm{J} 为幂零矩阵。

显然零幂矩阵是奇异矩阵。

且有

(E−J)−1=∑i=0k−1Ji\left( \bm{E} - \bm{J} \right)^{-1} = \sum_{i=0}^{k - 1} \bm{J}^i

证明：

(E−J)∑i=0k−1Ji=∑i=0k−1Ji−∑i=1kJi=J0−Jk=E\begin{aligned} \left( \bm{E} - \bm{J} \right) \sum_{i=0}^{k - 1} \bm{J}^i &= \sum_{i=0}^{k - 1} \bm{J}^i - \sum_{i=1}^{k} \bm{J}^i \\ &= \bm{J}^0 - \bm{J}^k \\ &= \bm{E} \end{aligned}

矩阵多项式

设 f(x)=∑i=0naixif(x) = \displaystyle \sum_{i=0}^{n} a_i x^i，f(A)=Of(\bm{A}) = \bm{O}，则 f(t)≠0  ⟹  A−tEf(t) \ne 0 \implies \bm{A} - t \bm{E} 可逆。

证明：

f(A)=Of(\bm{A}) = \bm{O} 可得

(A−tE)[∑i=1n(∑j=intj−iaj)Ai−1]+E∑k=0ntkak=O\left( \bm{A} - t \bm{E} \right)\left[ \sum_{i=1}^{n}\left( \sum_{j=i}^{n} t^{j - i}a_j \right)\bm{A}^{i - 1} \right] + \bm{E} \sum_{k=0}^{n}t^k a_k = \bm{O}

这起码是我一个月以前写的了，显然是跳步了，我也懒得检验或解释了。

总而言之，这一步就是将矩阵多项式提个公因式 A−tE\bm{A} - t \bm{E}。

还是解释一下吧。E\bm{E} 可以看作 A0\bm{A}^0，从而可以看作是把多项式提出一个 ax+bax + b 的因式，外带一个常数项。

例如 x4+8x3+3x2+6x+2x^4 + 8x^3 + 3x^2 + 6x + 2，打算提出一个 x+1x + 1，则形式应该为 (x+1)(ax3+bx2+cx+d)+e(x + 1)(ax^3 + bx^2 + cx + d) + e。

显然 a=1a = 1，那么三次项就有了一个 ax3=x3ax^3 = x^3，还差 8x3−x3=7x38x^3 - x^3 = 7x^3，由 bx2⋅xbx^2 \cdot x 提供，则 b=7b = 7。

同理，c=−4c = -4，d=10d = 10，e=−8e = -8。

也即 x4+8x3+3x2+6x+2=(x+1)(x3+7x2−4x+10)−8x^4 + 8x^3 + 3x^2 + 6x + 2 = (x + 1)(x^3 + 7x^2 - 4x + 10) - 8。

随即若 f(t)=∑k=0ntkak≠0f(t) = \displaystyle \sum_{k=0}^{n} t^k a_k \ne 0，则有

(A−tE)−1=−1f(t)∑i=1n(∑j=intj−iaj)Ai−1\left( \bm{A} - t \bm{E} \right)^{-1} = - \dfrac{1}{f(t)} \sum_{i=1}^{n}\left( \sum_{j=i}^{n} t^{j - i}a_j \right)\bm{A}^{i - 1}

这个命题不满足等价。也即 A−tE\bm{A} - t \bm{E} 可逆 ̸  ⟹  f(t)≠0\nimplies f(t) \ne 0。

例如 f(x)=x2−3x+2f(x) = x^2 - 3x + 2，A=2E\bm{A} = 2 \bm{E} 满足 f(A)=Of(\bm{A}) = \bm{O}，而且 t=1t = 1 时 A−tE=E\bm{A} - t \bm{E} = \bm{E} 可逆，但 f(1)=0f(1) = 0。

上面这个 tip 用了我自己一个宏来表示「无法推出」，定义为 \mathbin{\kern13mu\not\kern-13mu\implies}，然而导致博文后面的内容都无法显示，原因不明。

上一次出现这个问题还是因为我用了 \fcolorbox，我以为是里面的 $ ... $ 的问题，把 \fcolorbox 换成了 \boxed 就解决了，不过就没了人教版教科书那样定理的颜色边框。而这次比较神奇。

\mathbin 出自 Class Assignment，意思是指明这个为 binary，也即「二元运算符」。看来是不可以在里面使用 Spacing，我大致试了几个都不行。然而有例外，比如 \par 的定义是 \mathbin{/\kern-5mu/}，但是可以正常显示，如 / ⁣/\mathbin{/\kern-5mu/}（这个用的不是宏，而是直接输入）。于是我猜测是不可以同时有 \not。

真糟心，于是我只好把 Blog 的 \mathbin 全删了。

矩阵的分解

设 A\bm{A} 为 m×nm \times n 矩阵，r⁡(A)=r\rank(\bm{A}) = r，则存在 mm 阶可逆矩阵 P\bm{P} 和 nn 阶可逆矩阵 Q\bm{Q}，使 A=PΛQ\bm{A} = \bm{P} \bm{\Lambda} \bm{Q}，其中

Λ=[ErOOO]\bm{\Lambda} = \begin{bmatrix} \bm{E}_r & \bm{O} \\ \bm{O} & \bm{O} \end{bmatrix}

后记

这是本篇博文唯一一个二级标题，正文的二级标题我不知道怎么取，就干脆不要二级标题了（正文我一般不用一级标题，一级标题我一般默认为标题，除了「记事板」，一级标题作为年份）。

2023 年国家公祭日记

重新整理博客结构时，为了使目录不要太抽象，补了一个二级标题「笔记」在上面。

这篇看起来好像没啥特别的。实际上就内容而言确实，但是却特殊在本篇内容是我完全在 WSL 上完成的。

效率有提高吗？似乎没有，预览速度感觉差不多，也是内容一多就卡；UltiSnips 一开始的 Tabstop 似乎流畅了一点，也不知道是不是错觉，只不过到后面写多了还是会出现 Tabstop 迟滞、乱跳的现象。

不过我敢肯定写 LaTeX\LaTeX 效率绝对是会快一点的。其一，我自己也测试过了，WSL 的 LaTeX\LaTeX 编译速度比 Windows 快多了；其二，写 LaTeX\LaTeX coc 会给补全提示，WSL 下补全菜单性能比 Windows 好多了，Windows 下遍历选项延迟非常明显，而 WSL 流畅多了。

WSL 还有点不同就是我开了 conceal，gVim 我是关着的，因为不知道为什么，一些字符无法显示，WSL 因为在终端就没问题。

效率下降的点也是有的。由于我的 WSLVim.ahk 的缺陷，我无法区分单独的 r 模式与 Normal 模式，导致如果简单替换一个汉字，WSL 还是得切语言，而且换完后还得切回来，这点确实是 gVim 比较厉害的。

至于双拼，大概现在只比以前全拼慢一点了吧，多熟练熟练。不过非常气愤的是 f: en g: eng h: ang j: an 这四个韵母是我比较早就记住了的，但是呢还是老是打错（不是因为分不清楚，我普通话还算可以的吧，大部分我还是分得清楚的，主要是要打时老是要停下来想一想）。

还有一点，Windows 终端下新版输入法，我双拼如果打了很长还没选，发现前面打错了，左右键移动看不到光标的移动，导致我只能盲猜，或者删了重打。我估计全拼也有这个问题，只不过双拼格外严重，因为我开了自动展开，导致我删错一个，后面就模样大变了，我也猜不出删了哪个。

由于后面的笔记与本篇关联性稍有下降（这篇主要是杂七杂八的定义和犄角旮旯的笔记，后面大的要来了，秩有一堆东西，还有高斯消元法什么的），再加上本篇内容也比较长了，要是要预览就得注释一部分了，所以我就另开了一篇。

如图所示，便是我写笔记的布局了。

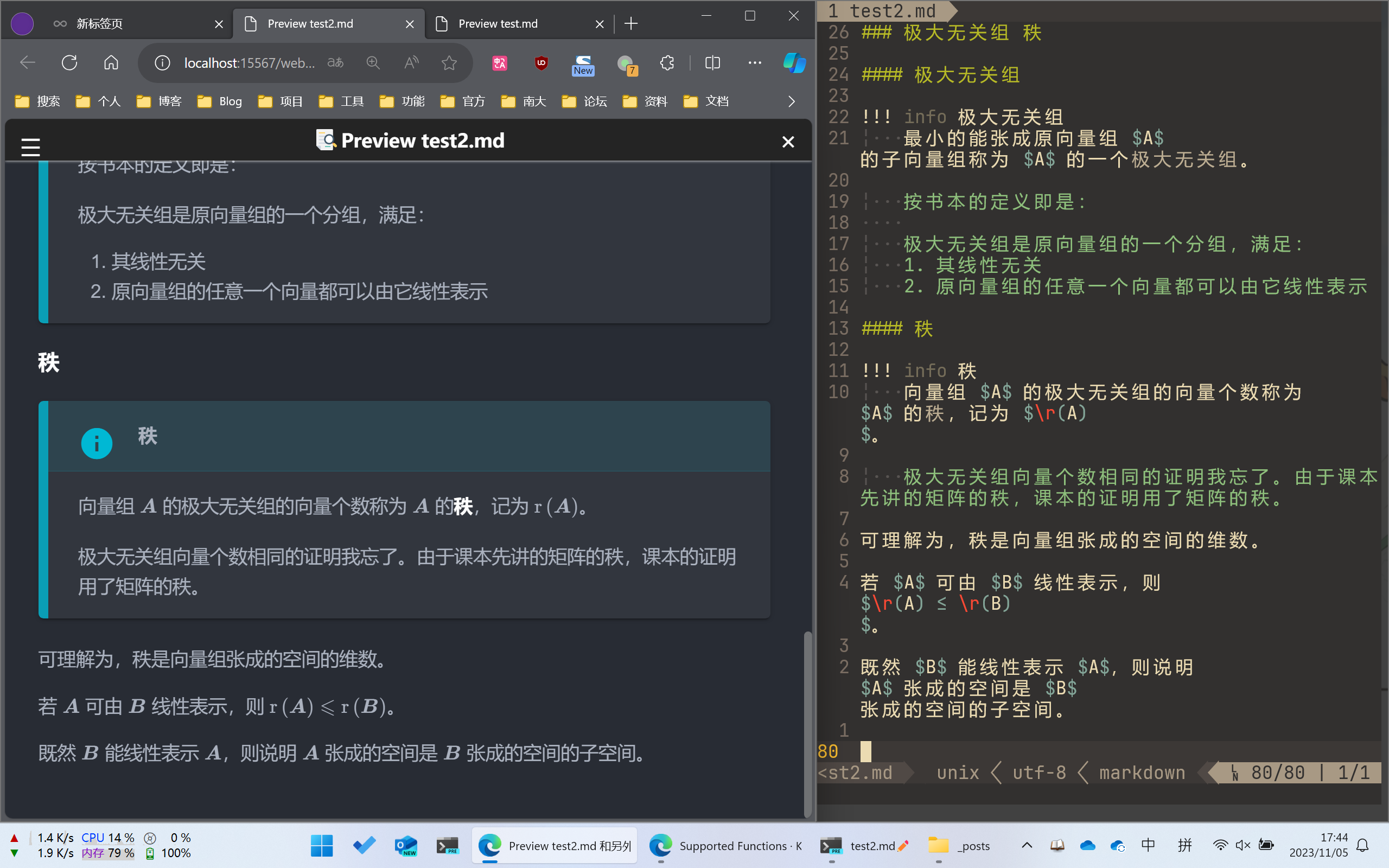
开两个浏览器，一个大概 2/3 屏预览，一个全屏查资料（比如我现在开着的就是 KaTeX\KaTeX 函数大全，查一些可能忘记了的命令。

WSL 运行在 Windows Terminal 上，大概占 1/3 屏。

开个 _posts 文件夹，或是方便打开 gVim 或是看看以前的博文，或是弄些图片，或是给 _imagecompression.py 加个新文件夹什么的。

写完后，一般流程就是 Win + T 打开终端（也可以在 WSL 那里 Ctrl + Shift + 3，只不过就会有 UAC 了），然后直接一个 bpb（blog publish），或者有时候想看看在博客的效果，用 blk（blog look）。

然后 Win + R 输入 code 回车，打开 Blog 项目，commit 更新的内容，然后 push。

有时候开个小差，也可以用第二个浏览器去看点别的内容，或者打开 QQ 微信看看。

目前我对这套流程还是挺满意的，写笔记成为一个享受。然而今日午睡起来后，又玩手机玩了一个多小时才下床继续写。

可能会发现最近的笔记逻辑性比较差，不仅少了些必要的证明，也少了很多我个人的见解，因为我课本笔记都随便记的，这里一块那里一块，加上老师不是按课本讲的（课本那定义一个比一个抽象，像行列式、秩），而且已经过去蛮长时间了，我也记不清楚了，所以就只能这样了。

这便是临时抱佛脚的恶果吗。