偏序关系
偏序关系
非空集合 上的自反、反对称、传递关系称为 上的偏序关系(partial order),记为 。
常写作 ,读作「 小于等于 」。
使用 表示 。
这里的偏序称为非严格偏序或自反偏序,若将「自反」换成「反自反」,则称为严格偏序或反自反偏序。
偏序集
集合 及其上的偏序关系 称为 上的偏序集,记为 。
设 为非空集合 上的偏序关系,对 ,若有 或 ,则称 和 可比。
设 是 上的偏序关系,若 中任意两个元素都可比,则称 是 上的全序关系(或线性序,total order)
若 且不存在 使得 ,则称 覆盖(cover)。
哈斯图(Hasse)
- 自反性省略圈
- 反对称性省略箭头
- 传递性省略箭头和中间节点
特殊元素
是 上的偏序集 中的极大元,当且仅当 。
是 上的偏序集 中的极小元,当且仅当 。
极大(小)元不一定存在,有穷集合一定有极大(小)元。
极大(小)元不一定唯一。一个元素可以同时为极大和极小元。
是 上的偏序集 中的最大元,当且仅当 。
是 上的偏序集 中的最小元,当且仅当 。
最大(小)元不一定存在,若存在必唯一。
对于偏序集 与 的子集 ,若存在 使得 ,则称 是 的上界。
若 的上界构成的偏序集有最小元,则称 有上确界(最小上界,least upper bound)。
同理可定义下界和下确界(最大下界,greatest lower bound)。
良序
给定集合 上的偏序关系 ,若 的任意非空子集有最小元,则称 是 上的良序(well order)。
良序必为全序,全序不一定为良序(对于无穷集合,全序不一定有最小元)。
良序的逆关系也未必是良序,例如
链
设 是偏序集 的一个子集,若 中任意两个元素都可比,则称 构成一个链(chain)。
若链 不是任何其它链的子链,则称 是极大化的,即 外没有一个元素与 中所有元素都可比。
设 是偏序集 的一个子集,若 中任意两个元素都不可比,则称 构成一个反链(anti-chain)。
若反链 不是任何其它反链的子链,则称 是极大化的,即 外没有一个元素与 中所有元素都不可比。
有限偏序集中最长链的元素个数称为该偏序集的高度(height),最大反链的元素个数称为该偏序集的宽度(width)。
任务调度
- 链内步骤有顺序依赖
- 反链内步骤可并发执行
并发任务调度
并发调度(concurrent scheduling)是将 划分为 使得对于 。
即不可使得 (前的)中的任务依赖于 (后的)中的任务。
结束于 的最长链称为到达 的关键路径(critical path)。该路径除 之外的元素个数称为 的深度(depth)。
偏序的划分
Mirsky 定理
设有限偏序集 的高度为 ,则可将其划分为 个反链。
推论
对有限偏序集 ,对于任意 ,要么有长度大于 的链,要么有长度至少为 的反链。
从而可知,对于任意有限偏序集 ,要么有长度大于 的链,要么有长度至少为 的反链。
链覆盖是 中一组互不相交的链,它们一起包含了 中的所有元素。即对互不相交的链 ,有
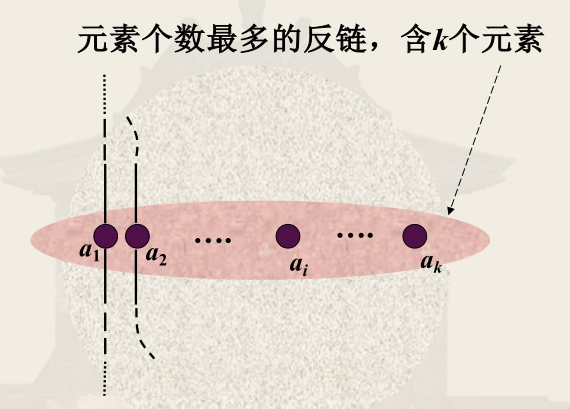
Dilworth 定理
设 是有限偏序集,其宽度为 ,则可将其划分为 个链。
归纳证明
Perles 1963 证明:
若 ,则 ,命题成立;
设命题对于 时成立,现证明对于 时成立。
对于某最长的反链 ,令
显然 且三者互不相交。
情况一:存在一个最长的反链 使得 与 均非空。
记 中元素为 ,在 上应用归纳假设(因为 非空,所以 ,即 )。不失一般性,有 一个链覆盖 ,且 是 的最大元素。
再在 上应用归纳假设,有 一个链覆盖 ,且 是 的最小元素。
于是 是一个链,且这 个链覆盖了 。
情况二:对于每一个最长的反链 , 都至少有一个为空。
在 中选择一个极大元素 ,再选择一个满足 的极小元素 ,则 构成一条链。
则 的宽度为 。
由归纳假设,可划分 为 条链,再加上 ,共有 条链即可。
按 中元素进行归纳证明。
设 为 中的一个极大元素,。
设 有一个大小为 的反链 ,并有一个规模为 的链覆盖 。
对任意 , 中大小为 的任意反链均有唯一元素属于 ,这些元素中最大元记为 。
于是 为反链。否则设 中有两个元素 ,根据 的定义, 中有一个大小为 的反链 , 为 和 的公共元素,假设 是 和 的公共元素,则 ,从而 ,与 是反链矛盾。
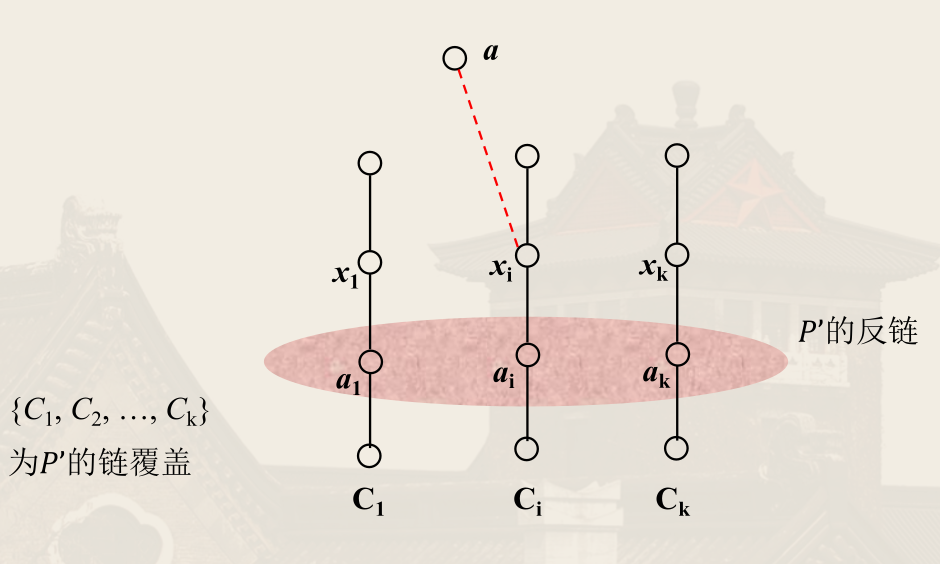
若 是 中的反链,则 的链覆盖 为规模为 的覆盖,得证。
若 不是 中的反链,即存在 (因 为极大元,不会有 )。
令 。显然 是 中的一条链。
中最大反链大小为 ( 中没有含 个元素的反链,否则与 的定义矛盾)。
由归纳假设, 有大小为 的一个链覆盖,该覆盖与 构成 的链覆盖(链数为 ),已知 是 中的反链,得证。
从而得到对任意有限偏序集 ,覆盖 的最小链数等于 的最长反链的长度(元素个数)。
