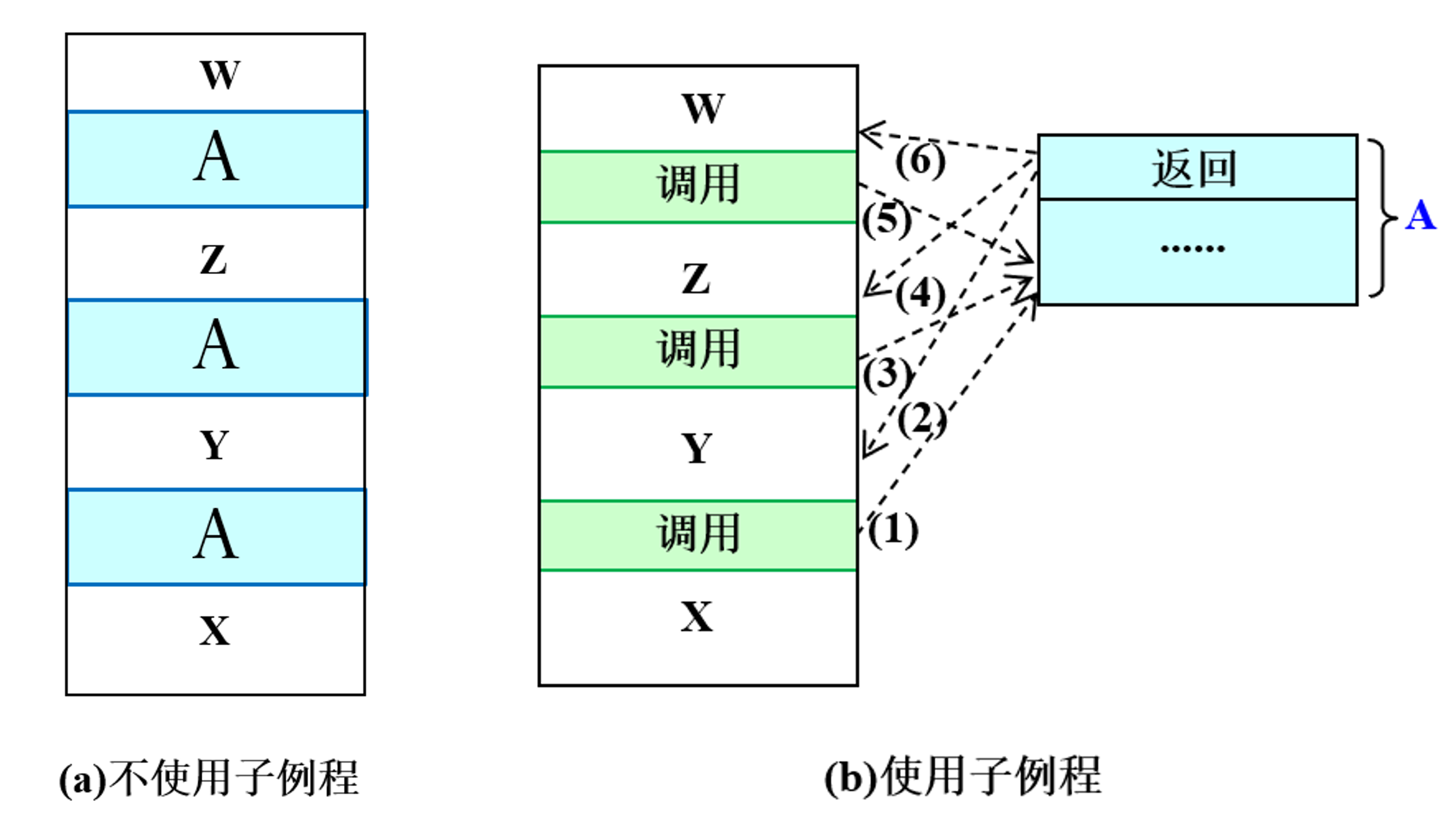
子例程
- 子程序（program, procedure）
- 将一个组件的功能与其实现的细节分隔开来
- 程序员只需理解组件的结构，不需要考虑其实现的细节，就能够把该组件作为一个程序块使用
- 子程序使程序员能够以模块化的方式写程序，提高了构建复杂计算系统的能力
- 子例程（subroutine, function）
- 在一个程序中，多次执行某个程序片段
- 在程序内，不必每次给出这个程序片段
- 通过多次调用该程序片段实现
调用-返回机制
通常设置 jal/jalr 目的寄存器为 x1，保存返回地址/链接；基址寄存器一般为 x5。
jal
- 计算出的地址被限制于内存一定范围中
- 偏移范围为 −2020∽220−2
jalr
伪指令 call 用于调用子例程
等价于
1
2
| auipc RD, offsetHi # offsetHi 为 offset 高 20 位
jalr x1, offsetLo(RD) # offsetLo 为 offset 低 12 位
|
伪指令 ret 用于从子例程返回
等价于
被调用者保存寄存器（callee-saved register）
由被调用者（callee）完成寄存器保存/恢复工作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| 01 .data
02 .align 2
03 SaveReg1: .word 0 # 保存寄存器的空间
04 #
05 .text
06 .align 2
07 # 省略代码，x8 <- x
08 addi x10, x0, 3 # x10 <- 3，被乘数
09 addi x11, x0, -2 # x11 <- -2，乘数
0A call Multiply
0B ...... # 使用 x8 做计算
0C ...... # 下一个任务
0D #
0E Multiply: la x5, SaveReg1
0F sw x8, 0(x5) # callee save
10 andi x9, x9, 0 # x9，积
11 Mloop: beqz x11, Mexit # x11，乘数
12 andi x8, x11, 1
13 beqz x8, Mnext
14 add x9, x9, x10 # x10，被乘数
15 Mnext: srli x11, x11, 1
16 slli x10, x10, 1
17 j Mloop
18 Mexit: lw x8, 0(x5) # 寄存器恢复
19 ret
|
0E 和 0F 行将 x8 的值 x 保存到预留的空间中；18 行将 x8 的值恢复。
参数和返回值
1
2
3
4
5
6
7
8
| ...... ......
08 addi x10, x0, 3 # x10 <- 3，被乘数
09 addi x11, x0, -2 # x11 <- -2，乘数
0A call Multiply # 调用子例程
...... ......
10 andi x9, x9, 0 # x9，积
14 add x9, x9, x10 # x10，被乘数
19 ret # 从子例程返回调用者
|
- 对于 Multiply 子例程：
- 对于调用 Multiply 子例程的程序
- 先传递参数值，即为 x10 和 x11 赋值
- 调用返回后，通过返回值 x9 得到乘法计算结果
调用者保存寄存器（caller-saved register）
由调用者（caller）完成的寄存器保存/恢复工作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| ......
09 SaveReg2: .word 0, 0
......
1F la x6, SaveReg2
20 sw x11, 0(x6) # caller save
......
22 addi x11, x0, 10 # x11，乘数
23 call Multiply # x9 = x10 * 10
......
25 la x6, SaveReg2
26 lw x11, 0(x6) # 寄存器恢复
......
29 addi x11, x11, 1 # x11 指向下一个字符
......
2C DoneS2I: ret
|
09 行使用数据区的存储单元作为保存寄存器的空间；1F 和 20 行将 x11 的值保存到预留的空间中；25 和 26 行：将 x11 的值恢复。
在 23 行执行 call 后，x1 被改变（为 24 行 PC 值），待该子例程在 2C 行 ret 返回时，会返回到 24 行，发生了错误！
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| ......
09 SaveReg2: .word 0, 0
......
1F la x6, SaveReg2
......
21 sw x1, 4(x6) # caller save
......
23 call Multiply # x9 = x10 * 10
......
25 la x6, SaveReg2
......
27 lw x1, 4(x6) # 寄存器恢复
......
2C DoneS2I: ret
|
09 行使用数据区的存储单元作为保存寄存器的空间；21 行将 x1 的值保存到预留的空间中；27 行将 x1 的值恢复。
寄存器的保存/恢复
基本原则：如果一个寄存器内的值将在该寄存器的值被改变之后再次被用到，必须在其值被改变之前将其保存，在再次使用它之前将其恢复。
- 通过将寄存器的值存进内存，来保存它的值
- 通过将内存保留的值加载回寄存器，来恢复它的值
如果在子例程中又调用了子例程，必须采用 caller-saved（调用者保存）的策略，保存/恢复返回地址 x1
RISC-V 各寄存器的 Saved by 可见 5-指令集体系。
- caller-saved 寄存器
- 维护责任：调用者
- 调用者要在子例程的调用前/后，保存/恢复寄存器
- 被调用者不用关心这些寄存器旧值，可以直接覆写
- 必须在每次发生子例程调用前后都进行保存恢复
- callee-saved 寄存器
- 维护责任：被调用者
- 这些寄存器在使用前/后必须由被调用者保存/恢复
- 调用者可以认为子例程返回后这些寄存器是没有被改写的
- 在子例程调用时不需要调用者做任何动作
递归过程
即在一个子例程中调用这个子例程本身，称为递归子例程。
计算前 n 个正整数的和（本例取 n=3）：
Sn=Sn−1+n
初始条件 S1=1。
将 n 的值赋给 x10，调用 Sn 子例程，返回结果在 x11 中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| 01 .data
02 .align 2
03 SaveReg: .word 0
04 #
05 .text
06 .align 2
07 .globl main
08 main: addi x10, x0, 3 # n = 3
09 jal x1, Sn # call Sn
0A j end
0B #
0C Sn: la x5, SaveReg
0D sw x1, 0(x5) # caller save
0E addi x6, x0, 1
0F beq x10, x6, exit1 # n == 1 ?
10 addi x10, x10, -1 # n - 1
11 jal x1, Sn # 调用 S(n-1)
12 addi x10, x10, 1 # n
13 add x11, x11, x10 # S(n) = S(n-1) + n
14 j exit2
15 exit1: addi x11, x0, 1 # S(1) = 1
16 exit2: la x5, SaveReg
17 lw x1, 0(x5)
18 ret
|
但是这样每一层递归都将 x1 保存在了 SaveReg 中，导致了浅层次保存的结果被覆盖，因此会产生无限循环。
即递归调用子例程时，保存返回地址 x1 的指令将前一次保存的寄存器值覆盖了.
采用栈机制解决。
栈
栈是一种后进先出（LIFO, Last In, First Out）的数据结构，栈顶指针指向栈顶元素。
栈操作：
- 压栈（push）：将数据压入栈顶，栈顶指针加 1
- 出栈（pop）：将栈顶数据弹出，栈顶指针减 1
栈指针：
内存中的栈实现：
初始地址 x2 指向 0xBFFF FFF0。栈从高地址向低地址，即栈顶地址最小，栈顶在下（底）。
将保存在 x9 中的数值压栈：
1
2
| push: addi x2, x2, -4
sw x9, 0(x2)
|
将栈顶的数值弹出到 x9：
1
2
| pop: lw x9, 0(x2)
addi x2, x2, 4
|
栈协议：
- 是一组对内存的访问控制规则
- 满足后进先出（LIFO）原则
- 包含方法：PUSH, POP
改进后的递归调用：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| 01 lui x2, 0xc0000
02 addi x2, x2, -16 # x2 = 0xBFFF FFF0
03 addi x10, x0, 3 # n = 3
04 jal x1, Sn # call Sn
05 j end
06 #
07 Sn: addi x2, x2, -4 # push x1
08 sw x1, 0(x2)
09 addi x6, x0, 1
0A beq x10, x6, exit1 # n == 1 ?
0B addi x10, x10, -1 # n - 1
0C jal x1, Sn # S(n-1)
0D addi x10, x10, 1 # n
0E add x11, x11, x10 # S(n) = S(n-1) + n
0F j exit2
10 exit1: addi x11, x0, 1 # x11，S(1) = 1
11 exit2: lw x1, 0(x2) # pop x1
12 addi x2, x2, 4
13 ret
|
