Lambda 演算

发表于 更新于 阅读次数： Waline： 本文字数： 2.9k 阅读时长 ≈ 10 分钟

函数式编程（Functional Programming）

函数式编程是一种编程范型，其通过函数作用和复合来构造程序。它是声明式范型（Declarative Programming）的一种。与命令式的通过语句串改变状态不同，它使用一系列的函数表达式完成值到值的映射来表达计算。

函数作为一等公民（First-class Citizen）是函数式编程的一个重要特性。这意味着函数可以作为参数传递给其他函数，也可以作为返回值返回，可以被赋值给变量，可以被存储在数据结构中。

Lambda 演算

定义

  • 语法（Syntax）：构成合法程序的写法规则
  • 语义（Semantics）：描述所写程序的运行行为

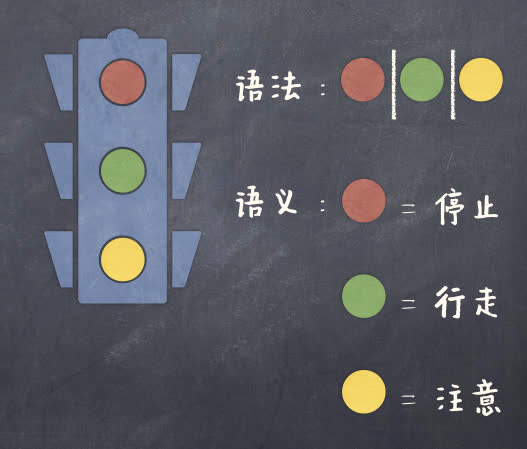
语法

λ\lambda 项或 λ\lambda 表达式的 BNF 范式（巴科斯范式，Backus-Naur Form）：

M,N⏟λ 项∷=x⏟变量∣λx.M∣MN\underbrace{M, N}_{\lambda \text{ 项}} \Coloneqq \underbrace{x}_{\text{变量}} \mid \lambda x.M \mid M N

具体解释：给定一个无限的变量集合 V\mathbb{V}，让 AA 为一个字符，其要么是 V\mathbb{V} 中的一个元素，要么是「()λ.()\lambda.」中一个字符，。让 A∗A* 为有限的字符串。那么隶属于 λ\lambda 表达式的字符串符 Λ∈A∗\Lambda \in A* 符合如下标准：

  1. 如果 x∈Vx \in V ，那么 x∈Λx \in \Lambda 。
  2. 如果 x∈Vx \in V 且 M∈ΛM \in \Lambda，那么 λx.M∈Λ\lambda x . M \in \Lambda。
  3. 如果 M,N∈ΛM, N \in \Lambda ，那么 MN∈ΛM N \in \Lambda。

(λx.M)(\lambda x . M)：Lambda 抽象（Lambda Abstraction）

increment = lambda x: x + 1

(MN)(M N)：Lambda 作用（Lambda Application）。MM 作用到 NN 上。

increment(3)

MM 尽可能右延伸，即 λx.MN\lambda x . M N 等价于 λx.(MN)\lambda x . (M N) 而非 (λx.M)N(\lambda x . M) N，λx.λy.x−y=λx.(λy.x−y)\lambda x . \lambda y . x - y = \lambda x . (\lambda y . x - y)

Lambda 作用左结合，即 MNPMNP 等价于 (MN)P(MN)P。

(λf.λx.fx)(λx.x+1)2→((λf.λx.fx)(λx.x+1))2→(λx.(λx′.x′+1)x)2→(λx.x+1)2→3\begin{aligned} (\lambda f . \lambda x . f x)(\lambda x . x+1) 2 &\to((\lambda f . \lambda x . f x)(\lambda x . x+1)) 2 \\ & \to\left(\lambda x .\left(\lambda x^{\prime} . x^{\prime}+1\right) x\right) 2 \\ & \to(\lambda x . x+1) 2 \\ & \to 3 \end{aligned}

高阶函数（Higher-order Function）：

  • 函数可以作为返回值返回
    • λx.λy.x−y\lambda x . \boxed{\lambda y . x - y}
  • 函数可以作为参数传递
    • (λf.λx.fx)(λx.x+1)2(\lambda f . \lambda x . f x) \boxed{(\lambda x . x + 1)} 2

柯里化（Currying）：将多参数函数转化为单参数函数的过程。即将 λ(x,y).x−y\lambda (x, y) . x - y 转化为 λx.λy.x−y\lambda x . \lambda y . x - y。

1
2
3
4
5
6
def subtract(x, y):
    return x - y
def curry(f):
    return lambda x: lambda y: f(x, y)

assert subtract(3, 2) == curry(subtract)(3)(2)

逆柯里化（Uncurrying）：将单参数函数转化为多参数函数的过程。即将 λx.λy.x−y\lambda x . \lambda y . x - y 转化为 λ(x,y).x−y\lambda (x, y) . x - y。

1
2
3
4
5
6
def subtract(x):
    return lambda y: x - y
def uncurry(f):
    return lambda x, y: f(x)(y)

assert subtract(3)(2) == uncurry(subtract)(3, 2)

在 λ\lambda 表达式，如 λx.x+y\lambda x. x + y 中

  • xx 为绑定变量（Bound Variable）
  • yy 为自由变量（Free Variable）
  • λx.M\lambda x. M 中 MM 为 xx 的绑定域（Scope），如 λx.x+y\lambda x. x + y 中 x+yx + y 为 xx 的绑定域。

α\alpha-变换（Alpha Conversion）：改变绑定变量的名字，如 λx.x+y\lambda x. x + y 可以变为 λz.z+y\lambda z. z + y。

自由变量不可重命名，如 λx.x+y\lambda x. x + y 不可变为 λx.x+z\lambda x. x + z。

令 fv(M)f_v(M) 为 MM 中自由变量的集合，则

  • fv(x)={x}f_v(x) = \left\lbrace x \right\rbrace
  • fv(λx.M)=fv(M)\{x}f_v(\lambda x. M) = f_v(M) \backslash \left\lbrace x \right\rbrace
  • fv(MN)=fv(M)∪fv(N)f_v(MN) = f_v(M) \cup f_v(N)

语义

β\beta-归约：(λx.M)N→M[N/x](\lambda x . M) N \to M[N / x]（N/xN / x 表示用 NN 替换 MM 中的 xx）

使用递归给出替换的严格定义：

x[N/x]=Ny[N/x]=y(MP)[N/x]=(M[N/x])(P[N/x])(λx.M)[N/x]=λx.M只替换自由变量，不替换绑定变量(λy.M)[N/x]={λy.(M[N/x])如果 y∉fv(N)λz.(M[z/y][N/x])如果 y∈fv(N) 且 z∉fv(M)∪fv(N)\begin{aligned} x [N / x] &= N \\ y [N / x] &= y \\ (M P) [N / x] &= (M [N / x]) (P [N / x]) \\ (\lambda x . M) [N / x] &= \lambda x . M \quad\text{只替换自由变量，不替换绑定变量}\\ (\lambda y . M) [N / x] &= \begin{cases} \lambda y . (M [N / x]) & \text{如果 } y \notin f_v(N) \\ \lambda z . (M [z / y] [N / x]) & \text{如果 } y \in f_v(N) \text{ 且 } z \notin f_v(M) \cup f_v(N) \\ \end{cases} \end{aligned}

最后一条是为了避免自由变量被绑定，如 (λx.x−y)[x/y](\lambda x . x - y) [x / y] 会变为 λx.x−x\lambda x . x - x。解决方法是将 yy 重命名为 zz，即 (λx.x−y)[z/y][x/y]=λx.x−z[x/y]=λy.y−z(\lambda x . x - y) [z / y] [x / y] = \lambda x . x - z [x / y] = \lambda y . y - z。

递归 β-归约规则{M→M′MN→M′NN→N′MN→MN′M→M′λx.M→λx.M′\text{递归 } \beta \text{-归约规则} \begin{cases} \begin{array}{c} M \to M'\\ \hline M N \to M' N \end{array}\\ \begin{array}{c} N \to N'\\ \hline M N \to M N' \end{array}\\ \begin{array}{c} M \to M'\\ \hline \lambda x . M \to \lambda x . M' \end{array} \end{cases}

  • β\beta-可约项（β\beta-redex）：以 (λx.M)N(\lambda x . M) N 形式出现的 λ\lambda 项（reducible expression）
  • β\beta-范式（β\beta-normal form）：不包含 β\beta-可约项的 λ\lambda 项（无法再进行 β\beta-归约的 λ\lambda 项）

汇聚定理（Church-Rosser Theorem）

β\beta-归约无论采用何种归约顺序，最终都会收敛到同一个 β\beta-范式。

M→∗M′={M→0M′iff. M=M′M→k+1M′iff. ∃M′′ M→M′′∧M′′→kM′M→∗M′iff. ∃k M→kM′M \to^{*} M' = \begin{cases} M \to^0 M' &\mathrm{iff.}\, M = M' \\ M \to^{k + 1} M' &\mathrm{iff.}\, \exists M''\, M \to M'' \land M'' \to^k M'\\ M \to^{*} M' &\mathrm{iff.}\, \exists k\, M \to^k M' \end{cases}

归约最多得到一个 β\beta-范式，即 β\beta-范式是唯一的。但有些归约得不到 β\beta-范式，如 (λx.xx)(λx.xx)(\lambda x . x x) \boxed{(\lambda x . x x)}。

有些归约策略可能会陷入无限循环，例如 (λu.λv.v)((λx.xx)(λx.xx))(\lambda u . \lambda v . v) \big((\lambda x . x x) \boxed{ (\lambda x . x x)}\big)

归约策略：

  • 应用序（Applicative Order）：总先归约最左、最内的可归约项（先归约参数，再归约函数）
    • 一个最外（outmost）的可约项是一个不被其他可约项包含的可约项。
    • 一个最内（innermost）的可约项是一个不包含其他可约项的可约项。
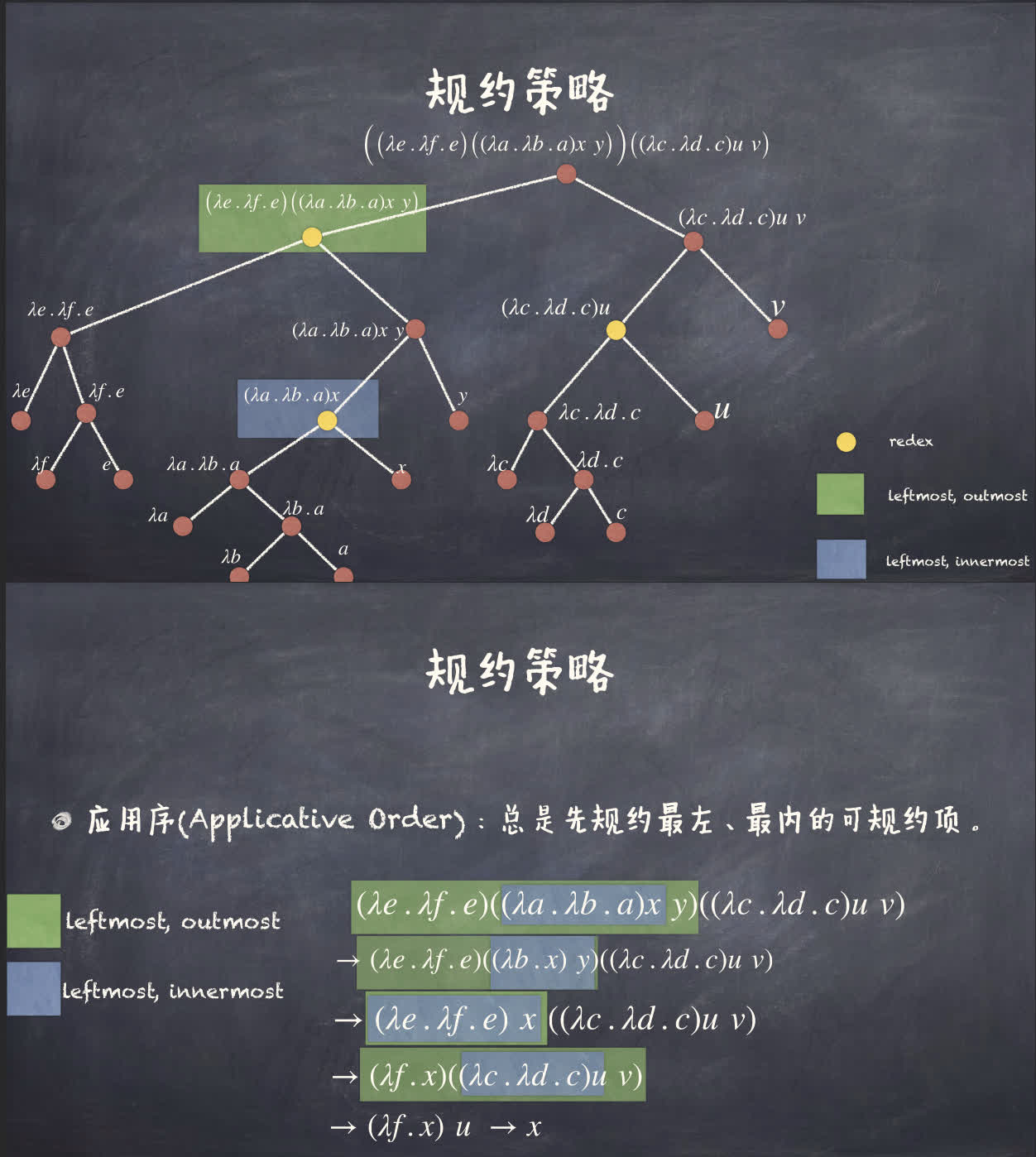
  • 正则序（Normal Order）：总先归约最左、最外的可归约项（参数未被归约，而是优先替换进函数体内）

如果 λ\lambda 表达式存在 β\beta-范式，那么按正则序归约总能归约到 β\beta-范式。

在参数使用不到的情况下，「正则序」（Call by name）会比「应用序」（Call by value）要高效，然而如果参数会用到，而且会重复的话「应用序」（Call by value）要比「正则序」（Call by name）要更加高效。

Call by need 是一种介于 Call by name 和 Call by value 之间的策略，它会将参数的值缓存起来，以避免重复计算。

基于 λ\lambda 演算的编程

Church 编码（Church Encoding）：使用 λ\lambda 演算来表示自然数、布尔值、元组、列表等数据结构。

  • 布尔值
    • T≜λx.λy.x\mathbf{T} \triangleq \lambda x . \lambda y . x
    • F≜λx.λy.y\mathbf{F} \triangleq \lambda x . \lambda y . y
  • 操作
    • if b then M else N≜bMN\text{if } b \text{ then } M \text{ else } N \triangleq b M N
    • Not≜λb.bFT\text{Not} \triangleq \lambda b . b \mathbf{F} \mathbf{T}
    • Not’≜λb.λx.λy.byx\text{Not'} \triangleq \lambda b . \lambda x . \lambda y . b y x
    • And≜λb.λc.bcF\text{And} \triangleq \lambda b . \lambda c . b c \mathbf{F}
    • Or≜λb.λc.bTc\text{Or} \triangleq \lambda b . \lambda c . b \mathbf{T} c

TMN→(λx.λy.x)MN→(λy.M)N→MFMN→(λx.λy.y)MN→(λy.N)N→NAnd Tb→(λb.λc.bcF)Tb→(λc.TcF)b→TbF→bAnd Fb→(λb.λc.bcF)Fb→(λc.FcF)b→FbF→FOr Tb→(λb.λc.bTc)Tb→(λc.TTc)b→TTb→TOr Fb→(λb.λc.bTc)Fb→(λc.FTc)b→FTb→b\begin{aligned} \mathbf{T} M N &\to (\lambda x . \lambda y . x) M N \\ &\to (\lambda y . M) N \\ &\to M \end{aligned} \quad \begin{aligned} \mathbf{F} M N &\to (\lambda x . \lambda y . y) M N \\ &\to (\lambda y . N) N \\ &\to N \end{aligned}\\ \begin{aligned} \text{And } \mathbf{T} b &\to (\lambda b . \lambda c . b c \mathbf{F}) \mathbf{T} b \\ &\to (\lambda c . \mathbf{T} c \mathbf{F}) b \\ &\to \mathbf{T} b \mathbf{F} \\ &\to b \end{aligned} \quad \begin{aligned} \text{And } \mathbf{F} b &\to (\lambda b . \lambda c . b c \mathbf{F}) \mathbf{F} b \\ &\to (\lambda c . \mathbf{F} c \mathbf{F}) b \\ &\to \mathbf{F} b \mathbf{F} \\ &\to \mathbf{F} \end{aligned}\\ \begin{aligned} \text{Or } \mathbf{T} b &\to (\lambda b . \lambda c . b \mathbf{T} c) \mathbf{T} b \\ &\to (\lambda c .\mathbf{T} \mathbf{T} c) b \\ &\to \mathbf{T} \mathbf{T} b \\ &\to \mathbf{T} \end{aligned} \quad \begin{aligned} \text{Or } \mathbf{F} b &\to (\lambda b . \lambda c . b \mathbf{T} c) \mathbf{F} b \\ &\to (\lambda c .\mathbf{F} \mathbf{T} c) b \\ &\to \mathbf{F} \mathbf{T} b \\ &\to b \end{aligned}

皮亚诺公理

  1. 00 是自然数。
  2. 对于任意自然数 nn，nn 的后继 n′n' 也是自然数。
  3. 对于每个自然数 m,nm, n，m=nm = n 当且仅当 mm 和 nn 有相同的后继。
  4. 00 不是任何自然数的后继。
  5. 若 AA 是一个性质，且 A(0)A(0) 成立，且对于任意自然数 nn，A(n)A(n) 成立时，A(n′)A(n') 也成立，则 A(n)A(n) 对于所有自然数 nn 都成立。

从而可以这样对自然数进行编码：

  1. 定义 00
  2. 定义后继函数 SS（递归 nn 次记作 SnS^n，从而有 n=Sn(0)n = S^n(0)）

邱奇数（Church numeral）

  1. 0≜λf.λx.x0 \triangleq \lambda f . \lambda x . x
  2. 1≜λf.λx.fx1 \triangleq \lambda f . \lambda x . f x
  3. 2≜λf.λx.f(fx)2 \triangleq \lambda f . \lambda x . f (f x)
  4. ⋯\cdots
  5. n≜λf.λx.fnxn \triangleq \lambda f . \lambda x . f^n x

当把函数和变量作用于 Church 数时，相当于对函数进行了 nn 次迭代，即

ngy=(λf.λx.fnx)gy=(λx.gnx)y=gn(y)\begin{aligned} n g y &= (\lambda f . \lambda x . f^n x) g y \\ &= (\lambda x . g^n x) y \\ &= g^n (y) \end{aligned}

定义自增运算（基于上面的迭代）

Inc⁡≜λn.λf.λx.f(nfx)Inc′⁡≜λn.λf.λx.nf(fx)\begin{aligned} \operatorname{Inc} \triangleq \lambda n . \lambda f . \lambda x . f (n f x)\\ \operatorname{Inc'} \triangleq \lambda n . \lambda f . \lambda x . n f (f x) \end{aligned}

定义加法运算（模仿自增运算，实际上上面省略了 11）

Add⁡≜λm.λn.λf.λx.nf(mfx)\begin{aligned} \operatorname{Add} \triangleq \lambda m . \lambda n . \lambda f . \lambda x . n f (m f x) \end{aligned}

定义乘法运算需要注意到 fm×n=(fm)nf^{m \times n} = (f^{m})^n，因此

Mult⁡≜λn.λm.λf.λx.n(mf)x\begin{aligned} \operatorname{Mult} \triangleq \lambda n . \lambda m . \lambda f . \lambda x . n (m f) x \end{aligned}

定义对零的判断

IsZero⁡≜λn.n(λx.F)T\begin{aligned} \operatorname{IsZero} \triangleq \lambda n . n (\lambda x . \mathbf{F}) \mathbf{T} \end{aligned}

IsZero⁡0=(λn.n(λx.F)T)0=0(λx.F)T=TIsZero⁡n=(λn.n(λx.F)T)n=n(λx.F)T=F\begin{aligned} \operatorname{IsZero} 0 &= (\lambda n . n (\lambda x . \mathbf{F}) \mathbf{T}) 0 \\ &= 0 (\lambda x . \mathbf{F}) \mathbf{T} \\ &= \mathbf{T} \end{aligned}\quad \begin{aligned} \operatorname{IsZero} n &= (\lambda n . n (\lambda x . \mathbf{F}) \mathbf{T}) n \\ &= n (\lambda x . \mathbf{F}) \mathbf{T} \\ &= \mathbf{F} \end{aligned}

对有序对（Pairs）的编码

Pair⁡≜λx.λy.λf.fxyπ0≜λp.pTπ1≜λp.pF\begin{aligned} \operatorname{Pair} &\triangleq \lambda x . \lambda y . \lambda f . f x y\\ \pi_0 &\triangleq \lambda p . p \mathbf{T}\\ \pi_1 &\triangleq \lambda p . p \mathbf{F} \end{aligned}

π0(Pair⁡MN)=(λp.pT)((λx.λy.λf.fxy)MN)=(λx.λy.λf.fxy)MNT=TMN=Mπ1(Pair⁡MN)=(λp.pF)((λx.λy.λf.fxy)MN)=(λx.λy.λf.fxy)MNF=FMN=N\begin{aligned} \pi_0 (\operatorname{Pair} M N) &= (\lambda p . p \mathbf{T}) ((\lambda x . \lambda y . \lambda f . f x y) M N )\\ &= (\lambda x . \lambda y . \lambda f . f x y) M N \mathbf{T}\\ &= \mathbf{T} M N\\ &= M \end{aligned}\quad \begin{aligned} \pi_1 (\operatorname{Pair} M N) &= (\lambda p . p \mathbf{F}) ((\lambda x . \lambda y . \lambda f . f x y) M N )\\ &= (\lambda x . \lambda y . \lambda f . f x y) M N \mathbf{F}\\ &= \mathbf{F} M N\\ &= N \end{aligned}

对元组（Tuples）的编码（仿照有序对）

Tuple⁡≜λx1.⋯ .λxn.λf.fx1⋯xnπi≜λp.p(λx1.⋯ .λxn.xi)\begin{aligned} \operatorname{Tuple} &\triangleq \lambda x_1 . \cdots . \lambda x_n . \lambda f . f x_1 \cdots x_n\\ \pi_i &\triangleq \lambda p . p (\lambda x_1 . \cdots . \lambda x_n . x_i) \end{aligned}

递归

但这样还不具有通用编程能力，因为不能递归。

之前定义的函数严格意义上其实是宏（Macro），是代表的 Lambda 表达式的缩写。

对于函数 f(x)f(x)，使得 x=f(x)x = f(x) 成立的 xx 称为 ff 的不动点（Fixed point）。

类似的，递归的实质在于 f=F(f)f = F(f)，即 ff 是 FF 的不动点。

将阶乘函数 Fact⁡\operatorname{Fact} 写成 f=F(f)f = F(f) 的形式：

Fact⁡=λn.if (n==0) then 1 else n×Fact⁡(n−1)=(λf.λn.if (IsZero⁡n) then 1 else n×f(n−1))Fact⁡=(λf.λn.(IsZero⁡n)1(n×f(n−1)))Fact⁡\begin{aligned} \operatorname{Fact} &= \lambda n . \text{if } (n == 0) \text{ then } 1 \text{ else } n \times \operatorname{Fact} (n - 1)\\ &= (\lambda f . \lambda n . \text{if } (\operatorname{IsZero} n) \text{ then } 1 \text{ else } n \times f (n - 1)) \operatorname{Fact}\\ &= (\lambda f . \lambda n . (\operatorname{IsZero} n) 1 (n \times f (n - 1))) \operatorname{Fact} \end{aligned}

虽然数学函数 ff 有可能没有不动点，但是 Lambda 表达式 FF 一定有不动点。

不动点组合子（Fixed-point combinator）是一个高阶函数 hh 满足，对于任意函数 ff，hfh f 是 ff 的不动点，即 hf=f(hf)h f = f (h f)。存在无数个不动点组合子。

  • 图灵不动点组合子 Θ\Theta
    • 令 A=λx.λy.y(xxy)A = \lambda x . \lambda y . y (x x y)
    • 令 Θ=AA\Theta = A A
  • 邱奇不动点组合子 Y\mathbf{Y}
    • 令 Y=λf.(λx.f(xx))(λx.f(xx))\mathbf{Y} = \lambda f . (\lambda x . f (x x)) (\lambda x . f (x x))

彩蛋

老师给了个链接，鳄鱼和蛋，「形象」地解释了 Lambda 演算的基础规则，看完了，挺绷不住的。

停机问题

Lambda 演算的停机问题，即判断一个 Lambda 表达式有没有 β\beta-范式。

假设存在一个高阶函数 hh 可以判定停机问题，其以一个 Lambda 表达式 ff 为参数（即 hfh f），当 ff 存在 β\beta-范式时返回 T\mathbf{T}，否则返回 F\mathbf{F}。

记

{I≜(λx.x)Ω≜(λx.xx)(λx.xx)\begin{cases} I \triangleq (\lambda x.x) \\ \Omega \triangleq (\lambda x.x x) (\lambda x.x x) \end{cases}

显然 II 有 β\beta-范式，Ω\Omega 无 β\beta-范式。

定义

P≜λx.h(xx)ΩIP \triangleq \lambda x . h (x x) \Omega I

考察 PPP P，若 PPP P 有 β\beta-范式，则 PPP P 会等于 Ω\Omega，即没有 β\beta-范式；若 PPP P 无 β\beta-范式，则 PPP P 会等于 II，即有 β\beta-范式。从而产生了矛盾，因此不存在这样的高阶函数 hh。