线性模型

发表于 更新于 阅读次数： Waline： 本文字数： 6.2k 阅读时长 ≈ 22 分钟

基本形式

给定由 dd 个属性描述的示例 x=(x1;x2;⋯ ;xd)\bm{x} = (x_1; x_2; \cdots; x_d)，其中 xix_i 是 x\bm{x} 的第 ii 个属性上的取值，线性模型（linear model）试图学得一个通过属性的线性组合来进行预测的函数，即

f(x)=w1x1+w2x2+⋯+wdxd+bf(\bm{x}) = w_1 x_1 + w_2 x_2 + \cdots + w_d x_d + b

一般用向量形式写成

f(x)=w⊺x+bf(\bm{x}) = \bm{w}^\intercal \bm{x} + b

其中 w=(w1;w2;⋯ ;wd)\bm{w} = (w_1; w_2; \cdots; w_d)。w,b\bm{w}, b 学得后，模型就得以确定。

线性模型形式简单、易于建模，有很好的可解释性（comprehensibility），蕴含着机器学习中一些重要的基本思想，许多功能更强大的非线性模型（nonlinear model）可在线性模型的基础上通过引入层级结构或高维映射而得。

线性回归

给定数据集 D={(x1,y1), (x2,y2), ⋯ , (xm,ym)}D = \left\lbrace (\bm{x}_1, y_1),\, (\bm{x}_2, y_2),\, \cdots,\, (\bm{x}_m, y_m) \right\rbrace，其中 xi=(xi1;xi2;⋯ ;xid), yi∈R\bm{x}_i = (x_{i1}; x_{i2}; \cdots; x_{id}),\, y_i \in \R。线性回归（linear regression）试图学得一个线性模型以尽可能准确地预测实值输出标记。

先考虑一种简单的情形（单一属性线性回归）：输入的属性数目只有一个。为了便于讨论，此时忽略关于属性的下标。

线性回归试图学得

f(xi)=wxi+bf(x_i) = w x_i + b

使得

f(xi)≃yif(x_i) \simeq y_i

确定 w,bw, b 的方法有很多，最常见的是最小二乘法（least squares method），即使得均方误差最小化：

(w∗,b∗)=arg min⁡(w,b)∑i=1m(f(xi)−yi)2(w^{*}, b^{*}) = \argmin_{(w, b)} \sum_{i=1}^{m} \left( f(x_i) - y_i \right)^2

求解 w,bw, b 使得 E(w,b)E_{(w, b)} 最小化的过程，称为线性回归模型的最小二乘「参数估计」（parameter estimation）。

过程

求偏导有

{∂E(w,b)∂w=2(w∑i=1mxi2−∑i=1m(yi−b)xi)∂E(w,b)∂b=2(mb−∑i=1m(yi−wxi))\left\lbrace\begin{aligned} \dfrac{\partial E_{(w, b)}}{\partial w} &= 2 \left( w \sum_{i=1}^{m} x_i^2 - \sum_{i=1}^{m} (y_i - b) x_i \right) \\ \dfrac{\partial E_{(w, b)}}{\partial b} &= 2 \left( m b - \sum_{i=1}^{m} (y_i - w x_i) \right) \end{aligned}\right.

令两式为零可得 w,bw, b 最优解的闭式（closed-form）解

{w=∑i=1myi(xi−xˉ)∑i=1mxi2−1m(∑i=1mxi)2b=1m∑i=1m(yi−wxi)\left\lbrace\begin{aligned} w &= \dfrac{\sum\limits_{i = 1}^m y_i (x_i - \bar{x})}{\sum\limits_{i = 1}^m x_i^2 - \frac{1}{m} \left( \sum\limits_{i = 1}^m x_i \right)^2} \\ b &= \dfrac{1}{m} \sum_{i=1}^{m} (y_i - w x_i) \end{aligned}\right.

其中 xˉ=1m∑i=1mxi\bar{x} = \frac{1}{m} \sum\limits_{i = 1}^m x_i 为 xx 的均值。

更一般的情形就是多元线性回归（multivariate linear regression），即输入的属性数目大于一个。此时，线性回归试图学得

f(xi)=w⊺xi+bf(\bm{x}_i) = \bm{w}^\intercal \bm{x}_i + b

使得

f(xi)≃yif(\bm{x}_i) \simeq y_i

过程

为了便于讨论，将 w,b\bm{w}, b 吸收入向量形式 w^=(w;b)\hat{\bm{w}} = (\bm{w}; b)。相应的，把数据集 DD 表示为一个 x×(d+1)x \times (d + 1) 大小的矩阵 X\mathbf{X}，其中每一行对应于一个示例，该行前 dd 个元素对应于示例的 dd 个属性值，最后一个元素恒置为 11，即

X=(x11x12⋯x1d1x21x22⋯x2d1⋮⋮⋱⋮⋮xm1xm2⋯xmd1)=(x1⊺1x2⊺1⋮⋮xm⊺1)\mathbf{X} = \begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1d} & 1 \\ x_{21} & x_{22} & \cdots & x_{2d} & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_{m1} & x_{m2} & \cdots & x_{md} & 1 \end{pmatrix} = \begin{pmatrix} \bm{x}_1^\intercal & 1 \\ \bm{x}_2^\intercal & 1 \\ \vdots & \vdots \\ \bm{x}_m^\intercal & 1 \end{pmatrix}

标记也写成向量形式 y=(y1;y2;⋯ ;ym)\bm{y} = (y_1; y_2; \cdots; y_m)。类似地有

w^∗=arg min⁡w^(y−Xw^)⊺(y−Xw^)\hat{\bm{w}}^{*} = \argmin_{\hat{\bm{w} }} (\bm{y} - \mathbf{X} \hat{\bm{w}})^\intercal (\bm{y} - \mathbf{X} \hat{\bm{w}})

令 Ew^=(y−Xw^)⊺(y−Xw^)E_{\hat{\bm{w} }} = (\bm{y} - \mathbf{X} \hat{\bm{w}})^\intercal (\bm{y} - \mathbf{X} \hat{\bm{w}})，求导有

∂Ew^∂w^=2X⊺(Xw^−y)\dfrac{\partial E_{\hat{\bm{w} } }}{\partial \hat{\bm{w} }} = 2 \mathbf{X}^\intercal (\mathbf{X} \hat{\bm{w}} - \bm{y})

令上式为零可得 w^\hat{\bm{w}} 最优解的闭式解。但涉及矩阵逆的计算，比单变量复杂一点。下面进行一个简单的讨论。

当 X⊺X\mathbf{X}^\intercal \mathbf{X} 为满秩矩阵（full-rank matrix）或正定矩阵（positive definite matrix）时，X⊺X\mathbf{X}^\intercal \mathbf{X} 可逆，此时有

w^∗=(X⊺X)−1X⊺y\hat{\bm{w}}^{*} = (\mathbf{X}^\intercal \mathbf{X})^{-1} \mathbf{X}^\intercal \bm{y}

令 x^i=(xi,1)\hat{\bm{x}}_i = (\bm{x}_i, 1)，则最终学得的多元线性回归模型为

f(xi)=x^i⊺(X⊺X)−1X⊺yf(\bm{x}_i) = \hat{\bm{x}}_i^\intercal (\mathbf{X}^\intercal \mathbf{X})^{-1} \mathbf{X}^\intercal \bm{y}

现实中 X⊺X\mathbf{X}^\intercal \mathbf{X} 往往不是满秩矩阵。例如在很多任务中会遇到大量的变量，甚至超出样例数，导致 X\mathbf{X} 列数多于行数，此时 X⊺X\mathbf{X}^\intercal \mathbf{X} 显然不满秩。此时可解出多个 w^\hat{\bm{w}}，它们都能使均方误差最小化，选择哪一个解作为输出，由学习算法的归纳偏好决定。常见的做法是引入正则化（regularization）项[1]。

对数线性回归（log-linear regression）类似，即

ln⁡y=w⊺x+b\ln y = \bm{w}^\intercal \bm{x} + b

这里就不再多谈。

更一般地，考虑单调可微函数 gg，令

y=g−1(w⊺x+b)y = g^{-1}(\bm{w}^\intercal \bm{x} + b)

这样得到的模型称为广义线性模型（generalized linear model）。其中函数 gg 称为联系函数（link function）。

对数几率回归

上一节讨论的是如何使用线性模型进行回归学习。对于分类任务，可以利用上面的广义线性模型，找到一个单调可微函数将分类任务的真实标记 yy 与线性回归模型的预测值联系起来。

考虑二分类问题，输出标记 y∈{0,1}y \in \left\lbrace 0, 1 \right\rbrace。对于线性回归模型，产生的预测值 z=w⊺x+bz = \bm{w}^\intercal \bm{x} + b 为实数，需要将其转换为 0/10 / 1 值。

一种方法是使用单位阶跃函数（unit-step function）：

y={0,z<0;0.5,z=0;1,z>0.y = \begin{cases} 0, & z < 0;\\ 0.5, & z = 0;\\ 1, & z > 0. \end{cases}

但单位阶跃函数不连续，不可微。于是希望找到能在一定程度上近似单位阶跃函数的替代函数（surrogate function），并希望它单调可谓。

对数几率函数（logistic function，对率函数）[2]是一个常用的替代函数：

y=11+e−zy = \dfrac{1}{1 + \e^{-z}}

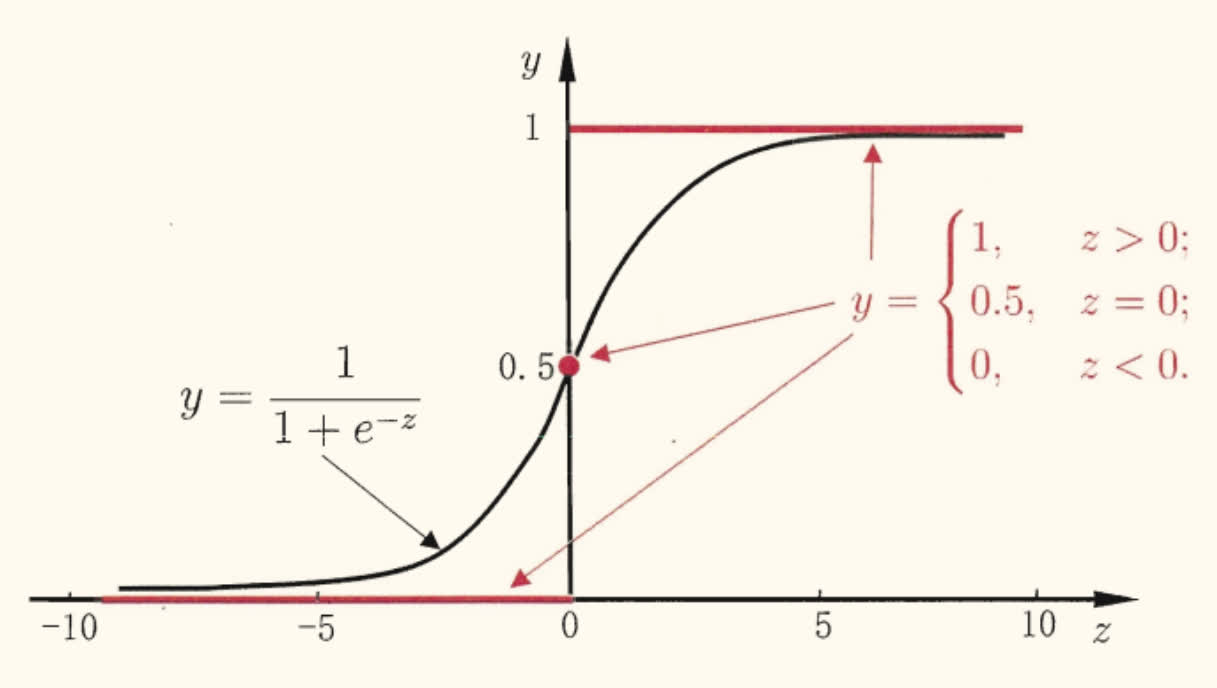
如图所示，对率函数是一种 Sigmoid 函数，即形似 S 的函数。它将 zz 值转化为一个接近 0/10 / 1 的 yy 值，并在 z=0z = 0 附近变化陡峭。

对于单调可谓函数 gg，广义线性模型有

y=g−1(w⊺x+b)\begin{equation} y = g^{-1}(\bm{w}^\intercal \bm{x} + b) \label{1} \end{equation}

将对率函数作为其中的 g−1g^{-1}，有

y=11+e−(w⊺x+b)\begin{equation} y = \dfrac{1}{1 + \e^{-(\bm{w}^\intercal \bm{x} + b)}} \label{2} \end{equation}

从而得到

ln⁡y1−y=w⊺x+b\ln \dfrac{y}{1 - y} = \bm{w}^\intercal \bm{x} + b

若将 yy 视为样本 x\bm{x} 作为正例的可能性，则 1−y1 - y 为其反例可能性，两者的比值 y1−y\dfrac{y}{1 - y} 称为几率（odds），这反映了 x\bm{x} 作为正例的相对可能性。同理有对数几率（log odds, a.k.a. logit）ln⁡y1−y\ln \dfrac{y}{1 - y}。

即式 (2)\eqref{2} 实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率，因此这个对应的模型才被称为对数几率回归（logistic regression, a.k.a. logit regression）。

虽然被称为是「回归」，但这实际上是一种学习方法。这种方法有很多优点，例如它是直接对分类可能性进行建模，无需事先假设数据分布，这样就避免了假设分布不准确所带来的问题；它不是仅预测出「类别」，而是可得到近似概率预测，这对许多需利用概率辅助决策的任务很有用；此外，对率函数是任意阶可导的凸函数，有很好的数学性质，现有的许多数值优化算法都可直接用于求取最优解。

接下来是确定式 (2)\eqref{2} 中的 w,b\bm{w}, b。若将其中的 yy 视为类后验概率估计 p(y=1∣x)p(y = 1 \mid \bm{x})，则有

ln⁡p(y=1∣x)p(y=0∣x)=w⊺x+b\ln \dfrac{p(y = 1 \mid \bm{x})}{p(y = 0 \mid \bm{x})} = \bm{w}^\intercal \bm{x} + b

从而有

{p(y=1∣x)=ew⊺x+b1+ew⊺x+bp(y=0∣x)=11+ew⊺x+b\left\lbrace\begin{aligned} p(y = 1 \mid \bm{x}) &= \dfrac{\e^{\bm{w}^\intercal \bm{x} + b}}{1 + \e^{\bm{w}^\intercal \bm{x} + b}} \\ p(y = 0 \mid \bm{x}) &= \dfrac{1}{1 + \e^{\bm{w}^\intercal \bm{x} + b}} \end{aligned}\right.

可以通过极大似然法（maximum likelihood method，最大似然估计）[3]来估计 w,b\bm{w}, b。给定数据集 {(xi,yi)}i=1m\left\lbrace (\bm{x}_i, y_i) \right\rbrace_{i=1}^m，对率回归模型最大化对数似然（log-likelihood）

ℓ(w,b)=∑i=1mln⁡p(yi∣xi;w,b)\ell(\bm{w}, b) = \sum_{i=1}^m \ln p (y_i \mid \bm{x}_i; \bm{w}, b)

即令每个样本属于其真实标记的概率越大越好。

为便于讨论，令 β=(w;b), x^=(x;1)\bm{\beta} = (\bm{w}; b),\, \hat{\bm{x}} = (\bm{x}; 1)，则 w⊺x+b\bm{w}^\intercal \bm{x} + b 可记为 β⊺x^\bm{\beta}^\intercal \hat{\bm{x}}。

再令 p1(x^;β)=p(y=1∣x^;β), p0(x^;β)=p(y=0∣x^;β)=1−p1(x^;β)p_1(\hat{\bm{x}}; \bm{\beta}) = p(y = 1 \mid \hat{\bm{x}}; \bm{\beta}),\, p_0(\hat{\bm{x}}; \bm{\beta}) = p(y = 0 \mid \hat{\bm{x}}; \bm{\beta}) = 1 - p_1(\hat{\bm{x}}; \bm{\beta})，则对数似然项可重写为

p(yi∣xi;w,b)=yip1(x^i;β)+(1−yi)p0(x^i;β)p(y_i \mid \bm{x}_i; \bm{w}, b) = y_i p_1(\hat{\bm{x}}_i; \bm{\beta}) + (1 - y_i) p_0(\hat{\bm{x}}_i; \bm{\beta})

书上这部分把我绕晕了……下面按自己的理解写。

将上式代入对率回归模型对数似然有

ℓ(β)=∑i=1mln⁡(yip1(x^i;β)+(1−yi)p0(x^i;β))=∑i=1mln⁡(yieβ⊺x^i1+eβ⊺x^i+(1−yi)11+eβ⊺x^i)\begin{aligned} \ell(\bm{\beta}) &= \sum_{i=1}^m \ln\left( y_i p_1(\hat{\bm{x}}_i; \bm{\beta}) + (1 - y_i) p_0(\hat{\bm{x}}_i; \bm{\beta}) \right)\\ &= \sum_{i=1}^m \ln\left( y_i \dfrac{\e^{\bm{\beta}^\intercal\hat{\bm{x}}_i}}{1 + \e^{\bm{\beta}^\intercal\hat{\bm{x}}_i}} + (1 - y_i)\dfrac{1}{1 + \e^{\bm{\beta}^\intercal\hat{\bm{x}}_i}}\right) \end{aligned}

然后呢，ln⁡\ln 移到 p0/1(x^i;β)p_{0 / 1}(\hat{\bm{x}}_i; \bm{\beta}) 上（可能我没搞懂其中的原理[4]），就有

ℓ(β)=∑i=1m(yiβ⊺x^i−ln⁡(1+eβ⊺x^i))\begin{aligned} \ell(\bm{\beta}) &= \sum_{i=1}^m \left( y_i\bm{\beta}^\intercal \hat{\bm{x}}_i - \ln\left( 1 + \e^{\bm{\beta}^\intercal \hat{\bm{x}}_i} \right) \right) \end{aligned}

最大似然估计即要使上式最大化。按书上的说法，将其取负以转化为最小值（相同的记号，不停变式子内容…）

ℓ(β)=∑i=1m(−yiβ⊺x^i+ln⁡(1+eβ⊺x^i))\ell(\bm{\beta}) = \sum_{i=1}^m \left( -y_i\bm{\beta}^\intercal \hat{\bm{x}}_i + \ln\left( 1 + \e^{\bm{\beta}^\intercal \hat{\bm{x}}_i} \right) \right)

这个是关于 β\bm{\beta} 的高阶可导连续凸函数，根据凸优化理论，可以使用经典的数值优化算法（如梯度下降法、牛顿法等）求得其最优解，得到

β∗=arg min⁡βℓ(β)\bm{\beta}^{*} = \argmin_{\bm{\beta}} \ell(\bm{\beta})

牛顿法

以牛顿法为例，其 t+1t + 1 轮迭代解的更新公式为

βt+1=βt−(∂2ℓ(β)∂β∂β⊺)−1∂ℓ(β)∂β\bm{\beta}^{t+1} = \bm{\beta}^t - \left( \dfrac{\partial^2 \ell(\bm{\beta})}{\partial \bm{\beta} \partial \bm{\beta}^\intercal} \right)^{-1} \dfrac{\partial \ell(\bm{\beta})}{\partial \bm{\beta}}

其中关于 β\bm{\beta} 的一二阶导数分别为

{∂ℓ(β)∂β=−∑i=1mx^i(yi−p1(x^i;β))∂2ℓ(β)∂β∂β⊺=∑i=1mx^ix^i⊺p1(x^i;β)(1−p1(x^i;β))\left\lbrace\begin{aligned} \dfrac{\partial \ell(\bm{\beta})}{\partial \bm{\beta}} &= - \sum_{i=1}^{m} \hat{\bm{x}}_i (y_i - p_1(\hat{\bm{x}}_i; \bm{\beta})) \\ \dfrac{\partial^2 \ell(\bm{\beta})}{\partial \bm{\beta} \partial \bm{\beta}^\intercal} &= \sum_{i=1}^{m} \hat{\bm{x}}_i \hat{\bm{x}}_i^\intercal p_1(\hat{\bm{x}}_i; \bm{\beta}) (1 - p_1(\hat{\bm{x}}_i; \bm{\beta})) \end{aligned}\right.

线性判别分析

线性判别分析（linear discriminant analysis, LDA）是一种经典的线性学习方法。

LDA 的思想：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近，异类样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别。

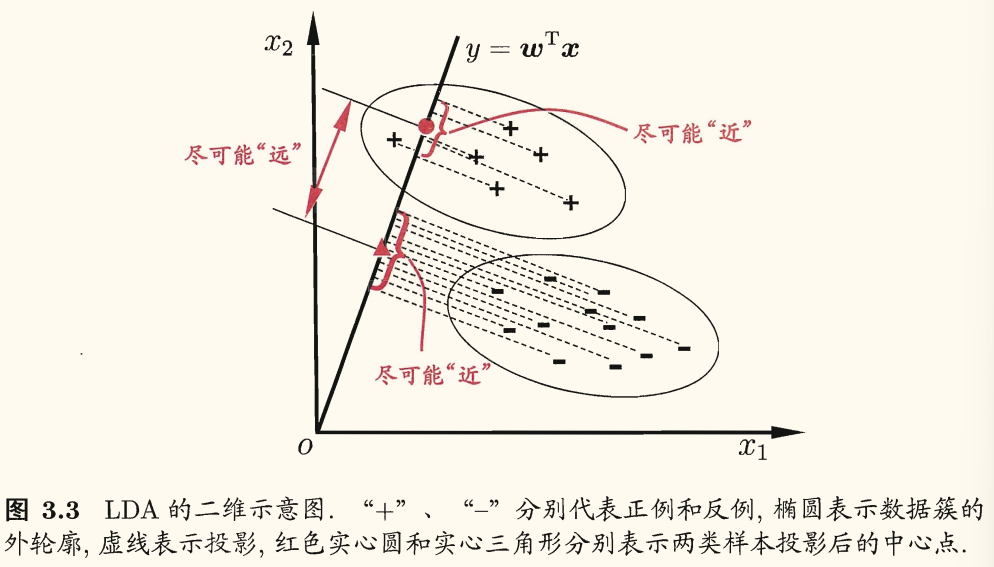
由于将样例投影到一条直线（低维空间），因此这也被视为一种「监督降维」技术（第 10 章）。

给定数据集 {(xi,yi)}i=1m, yi∈{0,1}\left\lbrace (\bm{x}_i, y_i) \right\rbrace_{i=1}^m,\, y_i \in \left\lbrace 0, 1 \right\rbrace，其中第 i∈{0,1}i \in \left\lbrace 0, 1 \right\rbrace 类示例有

  • 集合 XiX_i
  • 均值向量 μi\bm{\mu}_i
  • 协方差矩阵 Σi\bm{\Sigma}_i

若将数据投影到直线 w\bm{w} 上，则

  • 两类样本的中心在直线上的投影分别为 w⊺μ0\bm{w}^\intercal \bm{\mu}_0 和 w⊺μ1\bm{w}^\intercal \bm{\mu}_1
  • 两类样本的协方差在直线上的投影分别为 w⊺Σ0w\bm{w}^\intercal \bm{\Sigma}_0 \bm{w} 和 w⊺Σ1w\bm{w}^\intercal \bm{\Sigma}_1 \bm{w}。

若使同类样例投影点尽可能接近，可以让同类样例协方差尽可能小，即 w⊺Σ0w+w⊺Σ1w\bm{w}^\intercal \bm{\Sigma}_0 \bm{w} + \bm{w}^\intercal \bm{\Sigma}_1 \bm{w} 尽可能小；若使异类样例投影点尽可能远离，可以让异类样例中心点尽可能远离，即 ∥w⊺μ0−w⊺μ1∥22\left\lVert \bm{w}^\intercal \bm{\mu}_0 - \bm{w}^\intercal \bm{\mu}_1 \right\rVert^2_2[5] 尽可能大。

同时考虑二者，可得欲最大化的目标函数为

J=∥w⊺μ0−w⊺μ1∥22w⊺Σ0w+w⊺Σ1w=w⊺(μ0−μ1)(μ0−μ1)⊺ww⊺(Σ0+Σ1)w\begin{equation} \begin{aligned} J &= \dfrac{\left\lVert \bm{w}^\intercal \bm{\mu}_0 - \bm{w}^\intercal \bm{\mu}_1 \right\rVert^2_2}{\bm{w}^\intercal \bm{\Sigma}_0 \bm{w} + \bm{w}^\intercal \bm{\Sigma}_1 \bm{w}} \\ &= \dfrac{\bm{w}^\intercal(\bm{\mu}_0 - \bm{\mu}_1)(\bm{\mu}_0 - \bm{\mu}_1)^\intercal\bm{w}}{\bm{w}^\intercal(\bm{\Sigma}_0 + \bm{\Sigma}_1)\bm{w}} \end{aligned}\label{3} \end{equation}

定义类内散度矩阵（within-class scatter matrix）

Sw=Σ0+Σ1=∑x∈X0(x−μ0)(x−μ0)⊺+∑x∈X1(x−μ1)(x−μ1)⊺\begin{aligned} \mathbf{S}_w &= \bm{\Sigma}_0 + \bm{\Sigma}_1 \\ &= \sum_{\bm{x} \in X_0} (\bm{x} - \bm{\mu}_0)(\bm{x} - \bm{\mu}_0)^\intercal + \sum_{\bm{x} \in X_1} (\bm{x} - \bm{\mu}_1)(\bm{x} - \bm{\mu}_1)^\intercal \end{aligned}

与类间散度矩阵（between-class scatter matrix）

Sb=(μ0−μ1)(μ0−μ1)⊺\mathbf{S}_b = (\bm{\mu}_0 - \bm{\mu}_1)(\bm{\mu}_0 - \bm{\mu}_1)^\intercal

(3)\eqref{3} 可重写为

J=w⊺Sbww⊺Sww\begin{equation} J = \dfrac{\bm{w}^\intercal \mathbf{S}_b \bm{w}}{\bm{w}^\intercal \mathbf{S}_w \bm{w}} \label{4} \end{equation}

即 LDA 欲最大化的目标就是，Sb\mathbf{S}_b 与 Sw\mathbf{S}_w 的广义瑞利商（generalized Rayleigh quotient）。

过程

首先确定 w\bm{w}。注意到 (4)\eqref{4} 分子分母都是关于 w\bm{w} 的二次项，因此解与 w\bm{w} 长度无关，仅与其方向有关。不失一般性，令 w⊺Sww=1\bm{w}^\intercal S_w \bm{w} = 1，即最大化 (4)\eqref{4} 等价于

min⁡w−w⊺Sbws.t.w⊺Sww=1\min_{\bm{w}} - \bm{w}^\intercal \mathbf{S}_b \bm{w}\quad \text{s.t.}\quad \bm{w}^\intercal \mathbf{S}_w \bm{w} = 1

拉格朗日乘子法有拉格朗日函数（λ\lambda 是拉格朗日乘子）

L(w,λ)=−w⊺Sbw+λ(w⊺Sww−1)\mathcal{L}(\bm{w}, \lambda) = - \bm{w}^\intercal \mathbf{S}_b \bm{w} + \lambda (\bm{w}^\intercal \mathbf{S}_w \bm{w} - 1)

偏导有

{∂L∂w=2(λSww−Sbw)∂L∂λ=w⊺Sww−1\left\lbrace\begin{aligned} \dfrac{\partial \mathcal{L}}{\partial \bm{w}} &= 2 \left( \lambda \mathbf{S}_w \bm{w} - \mathbf{S}_b \bm{w} \right) \\ \dfrac{\partial \mathcal{L}}{\partial \lambda} &= \bm{w}^\intercal \mathbf{S}_w \bm{w} - 1 \end{aligned}\right.

即

Sbw=λSww\begin{equation} \mathbf{S}_b \bm{w} = \lambda \mathbf{S}_w \bm{w} \label{h1} \tag{h1} \end{equation}

注意到 Sbw\mathbf{S}_b \bm{w} 方向恒为 μ0−μ1\bm{\mu}_0 - \bm{\mu}_1，不妨设

Sbw=λ(μ0−μ1)\mathbf{S}_b \bm{w} = \lambda (\bm{\mu}_0 - \bm{\mu}_1)

代入 (h1)\eqref{h1} 有

w=Sw−1(μ0−μ1)\bm{w} = \mathbf{S}_w^{-1} (\bm{\mu}_0 - \bm{\mu}_1)

实践中通常是对 Sw\mathbf{S}_w 进行奇异值分解，即 Sw=UΣV⊺\mathbf{S}_w = \mathbf{U} \bm{\Sigma} \mathbf{V}^\intercal，其中 Σ\bm{\Sigma} 是一个实对角矩阵，对角线上的元素是 Sw\mathbf{S}_w 的奇异值，再由 Sw−1=VΣ−1U⊺\mathbf{S}_w^{-1} = \mathbf{V} \bm{\Sigma}^{-1} \mathbf{U}^\intercal 得到 Sw−1\mathbf{S}_w^{-1}。

LDA 的贝叶斯决策理论解释：两类数据同先验、满足高斯分布且协方差相等时，LDA 达到最优分类。

推广到多分类任务

假定存在 NN 个类，第 ii 类示例数为 mim_i，先定义全局散度矩阵

St=Sb+Sw=∑i=1m(xi−μ)(xi−μ)⊺\begin{aligned} \mathbf{S}_t &= \mathbf{S}_b + \mathbf{S}_w\\ &= \sum_{i=1}^m (\bm{x}_i - \bm{\mu})(\bm{x}_i - \bm{\mu})^\intercal \end{aligned}

其中 μ\bm{\mu} 是所有示例的均值向量。

将类内散度矩阵 Sw\mathbf{S}_w 重定义为每个类别的散度矩阵之和，即

Sw=∑i=1NSwi\mathbf{S}_w = \sum_{i=1}^N \mathbf{S}_{w_i}

其中

Swi=∑x∈Xi(x−μi)(x−μi)⊺\mathbf{S}_{w_i} = \sum_{\bm{x} \in X_i} (\bm{x} - \bm{\mu}_i)(\bm{x} - \bm{\mu}_i)^\intercal

从而有

Sb=St−Sw=∑i=1Nmi(μi−μ)(μi−μ)⊺\begin{aligned} \mathbf{S}_b &= \mathbf{S}_t - \mathbf{S}_w\\ &= \sum_{i=1}^N m_i (\bm{\mu}_i - \bm{\mu})(\bm{\mu}_i - \bm{\mu})^\intercal \end{aligned}

从而多分类 LDA 有多种实现方法：使用 Sb,Sw,St\mathbf{S}_b, \mathbf{S}_w, \mathbf{S}_t 三者中的任何两个即可。

常见的一种实现是采用优化目标

max⁡Wtr⁡(W⊺SbW)tr⁡(W⊺SwW)\max_{\mathbf{W}} \dfrac{\trace(\mathbf{W}^\intercal \mathbf{S}_b \mathbf{W})}{\trace(\mathbf{W}^\intercal \mathbf{S}_w \mathbf{W})}

其中 W∈Rd×(N−1)\mathbf{W} \in \R^{d \times (N - 1)}，tr⁡\trace 是矩阵的迹（trace）。上式可通过广义特征值问题求解：

SbW=λSwW\mathbf{S}_b \mathbf{W} = \lambda \mathbf{S}_w \mathbf{W}

W\mathbf{W} 的闭式解是 Sw−1Sb\mathbf{S}_w^{-1} \mathbf{S}_b 的 N−1N - 1 个最大广义特征值所对应的特征向量组成的矩阵。

多分类学习

现实中常遇到多分类学习任务。有些二分类学习方法可直接推广到多分类，但在更多情形下，我们是基于一些基本策略，利用二分类学习器来解决多分类问题。

不失一般性，考虑 NN 个类别 C1,C2,⋯ ,CNC_1, C_2, \cdots, C_N，多分类学习的基本思路是「拆解法」，即将多分类任务拆为若干个二分类任务求解。

上面的方法具体而言是：先对问题进行拆分，为拆出的每个二分类任务训练一个分类学习器，即分类器（classifier）。在测试时，对这些分类器的预测结果进行集成以获得最终的多分类结果。

因此关键在于「如何对多分类任务进行拆分」以及「如何对多个分类器进行集成」。本节主要介绍拆分策略。

最经典的拆分策略有一对一（One vs. One, OvO）、一对其余（One vs. Rest, OvR）和多对多（Many vs. Many, MvM）。

给定数据集 {(x1,y1), (x2,y2), ⋯ , (xm,ym)}, yi∈{C1,C2,⋯ ,CN}\left\lbrace (\bm{x}_1, y_1),\, (\bm{x}_2, y_2),\, \cdots,\, (\bm{x}_m, y_m) \right\rbrace,\, y_i \in \left\lbrace C_1, C_2, \cdots, C_N \right\rbrace。

OvO 将这 NN 个类别两两配对，从而产生 N(N−1)2\dfrac{N(N-1)}{2} 个二分类任务。测试阶段，新样本将同时提交给所有分类器，于是将得到 N(N−1)2\dfrac{N(N-1)}{2} 个分类结果，最终结果由投票决定：即把被预测得最多的类别作为最终的分类结果。

OvR 则是每次将一个类的样例作为正例、所有其他类的样例作为反例训练 NN 个分类器。测试时若仅有一个分类器预测为正例，则对应的类别标记作为最终分类结果。若有多个分类器预测为正例，则通常考虑各分类器的预测置信度，选择置信度最大的类别标记作为分类结果。

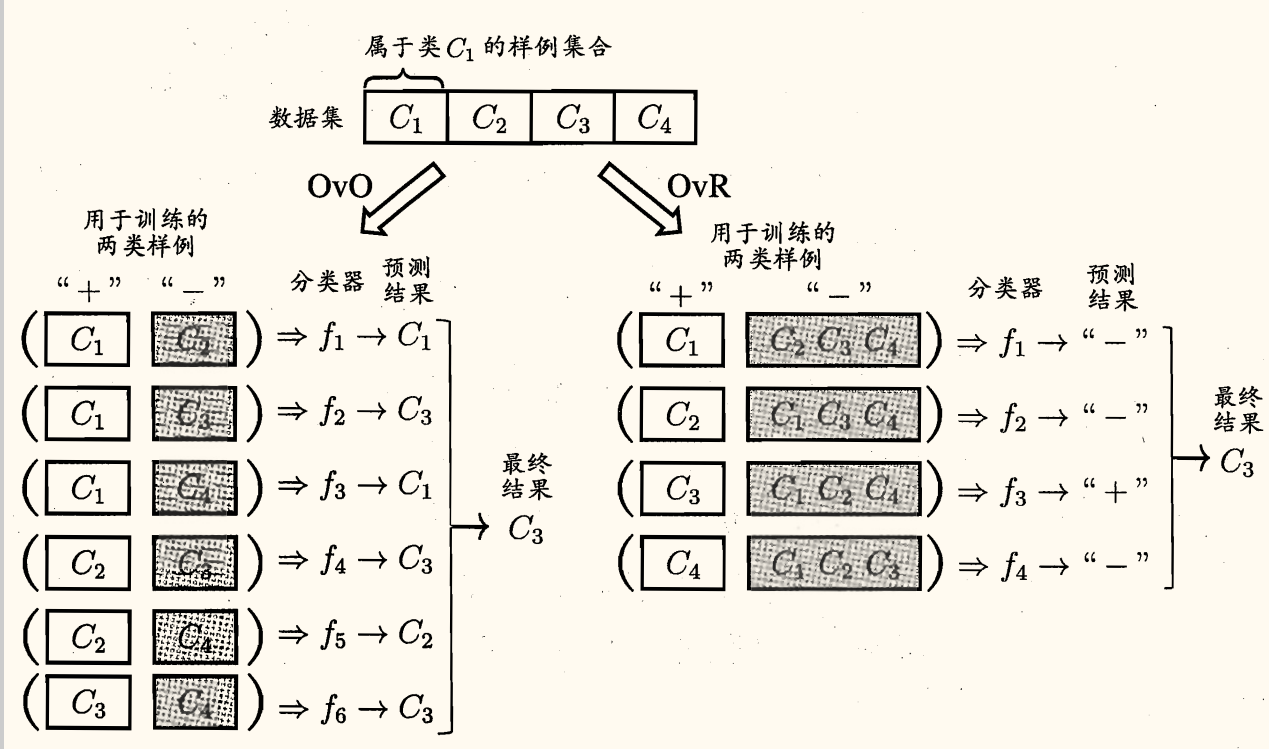
OvR 只需训练 NN 个分类器，而 OvO 需训练 N(N−1)2\dfrac{N(N-1)}{2} 个分类器，因此 OvO 的存储开销和测试时间开销通常比 OvR 更大。但在训练时， OvR 的每个分类器均使用全部训练样例，OvO 的每个分类器仅用到两个类的样例，因此类别很多时 OvO 的训练时间开销同时比 OvR 更小。

预测性能取决于具体的数据分布，多数情形下两者差不多。

MvM 是一种折中的策略。它每次将若干个类作为正类，若干个其他类作为反类。正、反类的构造必须有特殊的设计，下面是一种最常用的 MvM 技术——纠错输出码（Error Correcting Output Codes, ECOC）。

ECOC 是将编码的思想引入类别拆分，并尽可能在解码过程中具有容错性。工作过程主要分为两步：

  1. 编码：对 NN 个类别做 MM 次划分，每次划分将一部分类别划为正类，一部分划为反类，从而形成一个二分类训练集。一共产生 MM 个训练集，可训练 MM 个分类器。
  2. 解码：MM 个分类器分别对测试样本进行预测，这些预测标记组成一个编码。将这个编码与每个类别各自的编码进行比较，返回其中距离最小的类别作为最终预测结果。

对同等长度的编码，理论上来说，任意两个类别之间的编码距离越远，则纠错能力越强。因此，在码长较小时可根据这个原则计算出理论最优编码。然而，码长稍大一些就难以有效地确定最优编码，事实上这是 NP 难问题。不过，通常我们并不需获得理论最优编码，因为非最优编码在实践中往往已能产生足够好的分类器。

另一方面，并不是编码的理论性质越好，分类性能就越好，因为机器学习问题涉及很多因素，例如将多个类拆解为两个「类别子集」，不同拆解方式所形成的两个类别子集的区分难度往往不同，即其导致的二分类问题的难度不同；于是，一个理论纠错性质很好、但导致的二分类问题较难的编码，与另一个理论纠错性质差一些、但导致的二分类问题较简单的编码，最终产生的模型性能孰强孰弱很难说。

类别不平衡问题

前面介绍的分类学习方法基于一个共同的基本假设，即「不同类别的训练样例数目相当」。

若不同类别的训练样例数差别很大，会对学习过程造成困扰。例如有 998 个正例，2 个反例，一个分类器只需将所有样例都预测为正例，就能达到 99.8% 的准确率。但这样的分类器显然是无用的。

类别不平衡（class-imbalance）就是指分类任务中不同类别的训练样例数目差别很大的情况。不失一般性，本节假定正类样例较少，反类样例较多。

从线性分类器的角度进行讨论。

在用 y=w⊺x+by = \bm{w}^\intercal \bm{x} + b 对新样本 x\bm{x} 进行分类时，事实上是在用预测出的 yy 值与一个阈值进行比较，例如通常在 y>0.5y > 0.5 时判别为正例，否则为反例。

yy 实际上表达了正例的可能性，几率 y1−y\dfrac{y}{1 - y} 则反映了正例可能性与反例可能性之比值，阈值设置为 0.50.5 恰表明分类器认为真实正、反例可能性相同，即分类器决策规则为

若 y1−y>1\dfrac{y}{1 - y} > 1，则预测为正例。

然而，当训练集中正、反例数目不同时，令 m+,m−m^{+}, m^{-} 分别表示正、反例数目，则观测几率是 m+m−\dfrac{m^{+}}{m^{-}}。由于我们通常假设训练集是真实样本总体的无偏采样，因此观测几率就代表了真实几率。于是只要分类器的预测几率高于观测几率就应判定为正例，即

若 y1−y>m+m−\dfrac{y}{1 - y} > \dfrac{m^{+}}{m^{-}}，则预测为正例。

但是分类器基于第一个决策规则进行决策。因此需要对其观测值进行调整，使其基于第一个决策规则，但实际上是在执行第二个决策规则。只需令

y′1−y′=y1−y⋅m−m+\begin{equation} \dfrac{y'}{1 - y'} = \dfrac{y}{1 - y} \cdot \dfrac{m^{-}}{m^{+}} \label{5} \end{equation}

这就是类别不平衡学习的一个基本策略——再缩放（rescaling, 亦称再平衡 rebalance）。

然而，「训练集是真实样本总体的无偏采样」这个假设往往并不成立，即未必能有效地基于训练集观测几率来推断真实几率。

现有技术大体上有三类做法：

  • 欠采样（undersampling）：去除一些反例使得正、反例数目接近。
  • 过采样（oversampling）：增加一些正例使得正、反例数目接近。
  • 阈值移动（threshold-moving）：直接基于原始训练集进行学习，但在用训练好的分类器进行预测时，将式 (5)\eqref{5} 嵌入到其决策过程中。

欠采样法的时间开销通常远小于过采样法，因为前者丢弃了很多反例，使得分类器训练集远小于初始训练集，而过采样法增加了很多正例，其训练集大于初始训练集。

过采样法不能简单地对初始正例样本进行重复采样，否则会招致严重的过拟合；一方面，欠采样法若随机丢弃反例，可能丢失一些重要信息。

过采样法的代表性算法 SMOTE 是通过对训练集里的正例进行插值来产生额外的正例；欠采样法的代表性算法 EasyEnsemble 则是利用集成学习机制，将反例划分为若干个集合供不同学习器使用，这样对每个学习器来看都进行了欠采样，但在全局来看却不会丢失重要信息。

「再缩放」也是代价敏感学习（cost-sensitive learning）的基础。在代价敏感学习中将式 (5)\eqref{5} 中的 m−m+\dfrac{m^{-}}{m^{+}} 用 cost+cost−\dfrac{\mathrm{cost}^{+}}{\mathrm{cost}^{-}} 代替即可，其中 cost+,cost−\mathrm{cost}^{+}, \mathrm{cost}^{-} 分别表示将正、反例错分的代价。

  1. 等到第六章才会涉及。后面补充链接，若有的话。 ↩︎

  2. 名字跟「逻辑」很像，但没有关系。 ↩︎

  3. 有机会补充一下关于极大似然法的内容。 ↩︎

  4. 感觉可能像是利用了对数函数的凹性。 ↩︎

  5. 下标的 2 表示这是一个 L2L_2 范数。有关 LpL_p-范数的内容，可以简单参考维基百科。 ↩︎