支持向量机

发表于 更新于 Waline： 阅读次数： 本文字数： 6k 阅读时长 ≈ 22 分钟

间隔与支持向量

给定训练样本集 D={(xi,yi)}i=1mD = \left\lbrace (\bm{x}_i, y_i) \right\rbrace_{i=1}^m，其中 xi∈Rd\bm{x}_i \in \R^d，yi∈{−1,1}y_i \in \left\lbrace -1, 1 \right\rbrace，分类学习最基本的想法就是基于训练集 DD 在样本空间中找到一个划分超平面，将不同类别的样本分开。

如图所示，能将训练样本分开的划分超平面可能有很多：

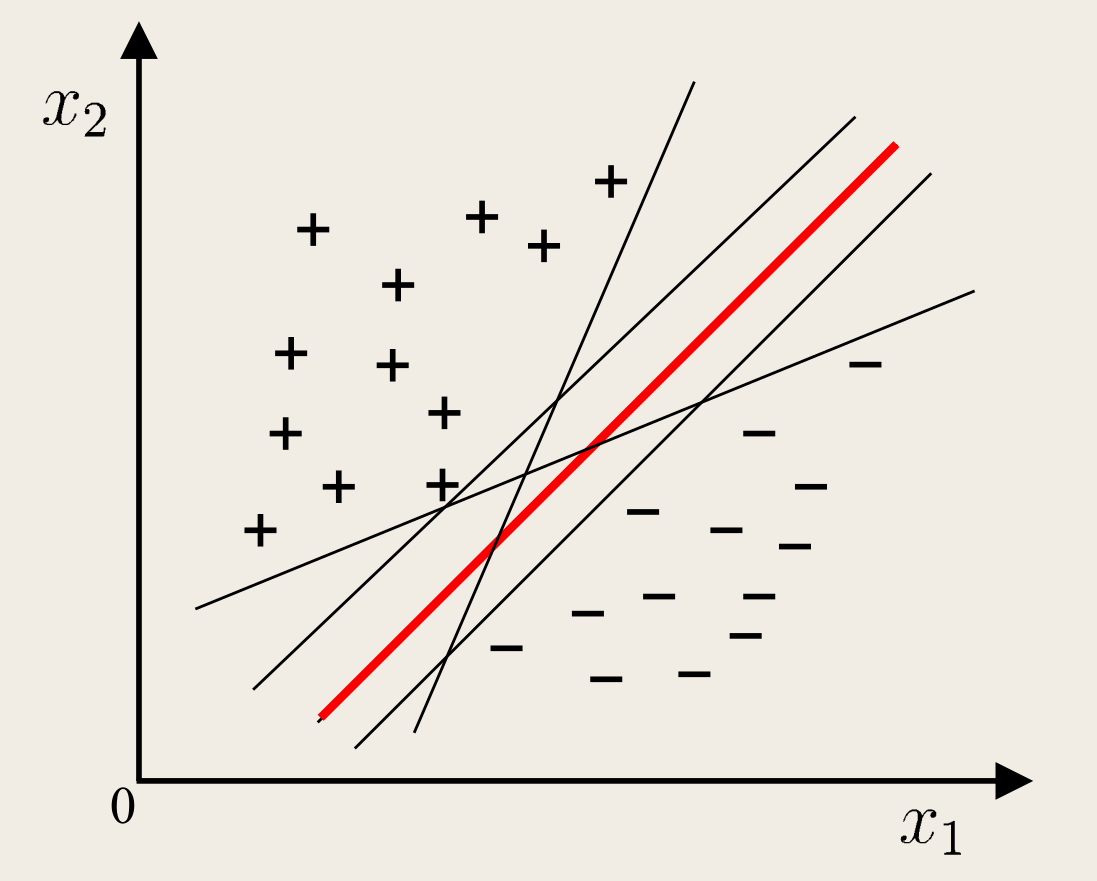
直观来说，应当选择对训练样本局部扰动的「容忍」性最好的。换言之，划分超平面所产生的分类结果是最鲁棒的，对未见示例的泛化能力最强。

样本空间中划分超平面可以描述为

w⊺x+b=0\bm{w}^\intercal \bm{x} + b = 0

其中 w=(w1;w2;… ;wd)\bm{w} = (w_1; w_2; \dots; w_d) 为法向量，决定了超平面的方向；bb 为位移项，决定了超平面与原点之间的距离。因此划分超平面可以由这两个参数确定，记为 (w,b)(\bm{w}, b)。

样本空间中任一点 x\bm{x} 到超平面 (w,b)(\bm{w}, b) 的距离可写为

r=∣w⊺x+b∣∥w∥r = \frac{\left| \bm{w}^\intercal \bm{x} + b \right|}{\left\| \bm{w} \right\|}

若超平面 (w,b)(\bm{w}, b) 可以将训练样本正确分类，即对于 (xi,yi)∈D(\bm{x}_i, y_i) \in D，若 yi=+1y_i = +1，则有 w⊺xi+b>0\bm{w}^\intercal \bm{x}_i + b > 0；若 yi=−1y_i = -1，则有 w⊺xi+b<0\bm{w}^\intercal \bm{x}_i + b < 0。令

{w⊺xi+b⩾+1,yi=+1w⊺xi+b⩽−1,yi=−1\begin{cases} \bm{w}^\intercal \bm{x}_i + b \ge +1, & y_i = +1 \\ \bm{w}^\intercal \bm{x}_i + b \le -1, & y_i = -1 \end{cases}

换种写法就是

yi(w⊺xi+b)⩾1,i=1,2,…,m\begin{equation} y_i(\bm{w}^\intercal \bm{x}_i + b) \ge 1, \quad i = 1, 2, \dots, m \label{1} \end{equation}

如下图所示，距离超平面最近的这几个训练样本点可使上式等号成立，它们被称为支持向量（support vector）：

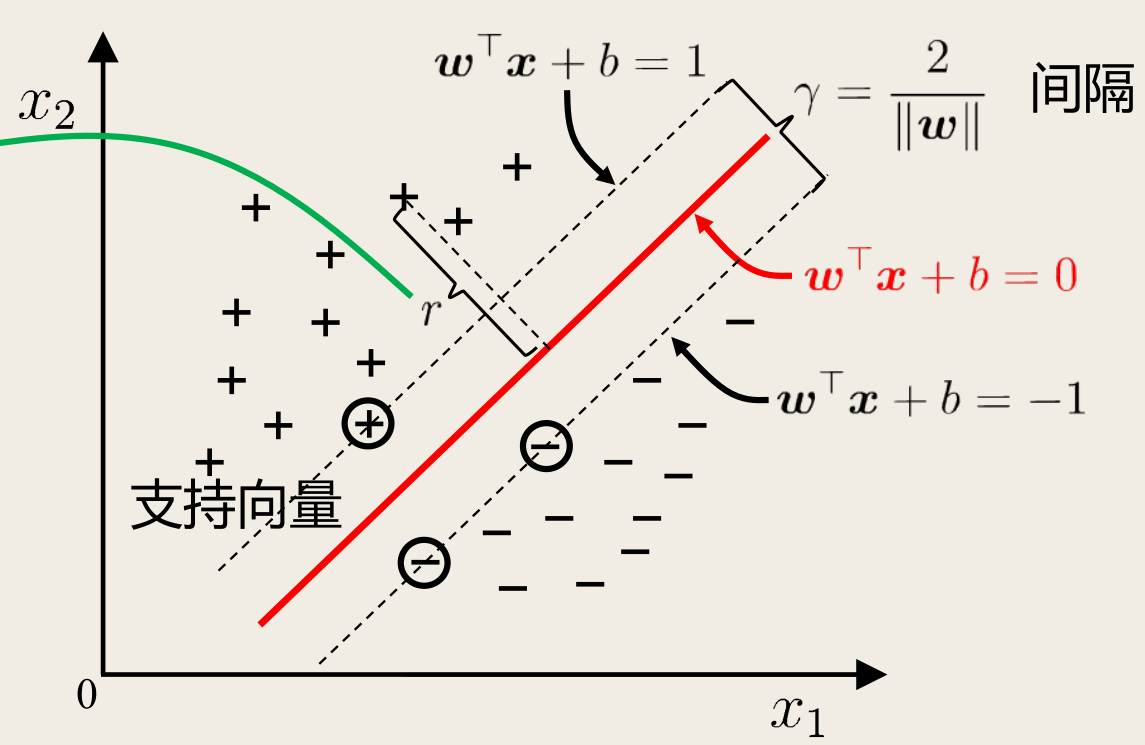
两个异类支持向量到超平面的距离之和为

γ=2∥w∥\gamma = \frac{2}{\left\| \bm{w} \right\|}

这被称为间隔（margin）。

也就是说，目标是找到具有「最大间隔」（maximum margin）的划分超平面，即找到满足 (1)\eqref{1} 约束的参数 w,b\bm{w}, b 使得 γ\gamma 最大：

max⁡w,b2∥w∥s.t.yi(w⊺xi+b)⩾1,i=1,2,…,m\max_{\bm{w}, b} \frac{2}{\left\| \bm{w} \right\|} \quad \text{s.t.} \quad y_i(\bm{w}^\intercal \bm{x}_i + b) \ge 1, \quad i = 1, 2, \dots, m

显然最大化间隔，只需要最小化 ∥w∥2\left\| \bm{w} \right\|^2 即可，因此上述优化问题等价于

min⁡w,b12∥w∥2s.t.yi(w⊺xi+b)⩾1,i=1,2,…,m\begin{equation} \min_{\bm{w}, b} \frac{1}{2} \left\| \bm{w} \right\|^2 \quad \text{s.t.} \quad y_i(\bm{w}^\intercal \bm{x}_i + b) \ge 1, \quad i = 1, 2, \dots, m \label{2} \end{equation}

这就是支持向量机（Support Vector Machine, SVM）的基本型。

对偶问题

数学知识待额外补充

拉格朗日乘子法

拉格朗日乘子法

最小化 f(x)f(\bm{x})，其中 f(x)f(\bm{x}) 为凸函数，约束条件为

{hi(x)⩽0,i=1,2,…,mgj(x)=0,j=1,2,…,n\begin{cases} h_i(\bm{x}) \le 0, & i = 1, 2, \dots, m\\ g_{j}(\bm{x}) = 0, & j = 1, 2, \dots, n \end{cases}

拉格朗日函数为

L(x,λ,μ)=f(x)+∑i=1mλihi(x)+∑j=1nμjgj(x)\mathcal{L}(\bm{x}, \bm{\lambda}, \bm{\mu}) = f(\bm{x}) + \sum_{i=1}^m \lambda_i h_i(\bm{x}) + \sum_{j=1}^n \mu_j g_j(\bm{x})

对偶问题为

max⁡λ,μinf⁡xL(x,λ,μ)s.t.λi⩾0,i=1,2,…,m\max_{\bm{\lambda}, \bm{\mu}} \inf_{\bm{x}} \mathcal{L}(\bm{x}, \bm{\lambda}, \bm{\mu})\quad \text{s.t.} \quad \lambda_i \ge 0, \quad i = 1, 2, \dots, m

Karush-Kuhn-Tucker(KKT) 条件为

  1. 稳定性：L(x,λ,μ)\mathcal{L}(\bm{x}, \bm{\lambda}, \bm{\mu}) 极值点梯度为零
  2. 原问题约束：hi(x)⩽0, gj(x)=0h_i(\bm{x}) \le 0,\, g_j(\bm{x}) = 0
  3. 对偶问题约束：λi⩾0\lambda_i \ge 0
  4. 互补松弛：λihi(x)=0\lambda_i h_i(\bm{x}) = 0

若满足 KKT 条件，则原问题与对偶问题的解相等。

首先引入拉格朗日乘子得到拉格朗日函数

L(w,b,α)=12∥w∥2+∑i=1mαi(1−yi(w⊺xi+b))\mathcal{L}(\bm{w}, b, \bm{\alpha}) = \frac{1}{2} \left\| \bm{w} \right\|^2 + \sum_{i=1}^m \alpha_i \left(1 - y_i(\bm{w}^\intercal \bm{x}_i + b) \right)

对 w,b\bm{w}, b 偏导为零得

{w=∑i=1mαiyixi0=∑i=1mαiyi\left\lbrace\begin{aligned} \bm{w} &= \sum_{i=1}^m \alpha_i y_i \bm{x}_i \\ 0 &= \sum_{i=1}^m \alpha_i y_i \end{aligned}\right.

代回拉格朗日函数得到对偶问题

max⁡α∑i=1mαi−12∑i=1m∑j=1mαiαjyiyjxi⊺xjs.t.∑i=1mαiyi=0, αi⩾0,i=1,2,…,m\begin{equation} \begin{aligned} &\max_{\bm{\alpha}} \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \bm{x}_i^\intercal \bm{x}_j \\ &\text{s.t.} \quad \sum_{i=1}^{m}\alpha_i y_i = 0,\, \alpha_i \ge 0, \quad i = 1, 2, \dots, m \end{aligned} \label{3} \end{equation}

过程

L(w,b,α)=12w⊺w−∑i=1mαiyiw⊺xi+∑i=1mαi−b∑i=1mαiyi=12w⊺w−w⊺∑i=1mαiyixi+∑i=1mαi−0=12w⊺w−w⊺w+∑i=1mαi=∑i=1mαi−12w⊺w=∑i=1mαi−12(∑i=1mαiyixi)⊺(∑i=1mαiyixi)=∑i=1mαi−12∑i=1m∑j=1mαiαjyiyjxi⊺xj\begin{aligned} \mathcal{L}(\bm{w}, b, \bm{\alpha}) &= \dfrac{1}{2}\bm{w}^\intercal \bm{w} - \sum_{i=1}^{m}\alpha_i y_i\bm{w}^\intercal \bm{x}_i + \sum_{i=1}^{m}\alpha_i - b\sum_{i=1}^{m}\alpha_i y_i \\ &= \dfrac{1}{2}\bm{w}^\intercal \bm{w} - \bm{w}^\intercal \sum_{i=1}^{m}\alpha_i y_i \bm{x}_i + \sum_{i=1}^{m}\alpha_i - 0\\ &= \dfrac{1}{2}\bm{w}^\intercal \bm{w} - \bm{w}^\intercal \bm{w} + \sum_{i=1}^{m}\alpha_i\\ &= \sum_{i=1}^{m}\alpha_i - \dfrac{1}{2}\bm{w}^\intercal \bm{w}\\ &= \sum_{i=1}^{m}\alpha_i - \dfrac{1}{2}\left(\sum_{i=1}^{m}\alpha_i y_i \bm{x}_i\right)^\intercal \left(\sum_{i=1}^{m}\alpha_i y_i \bm{x}_i\right)\\ &= \sum_{i=1}^{m}\alpha_i - \dfrac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_j y_i y_j \bm{x}_i^\intercal \bm{x}_j \end{aligned}

最终模型为

f(x)=w⊺x+b=∑i=1mαiyixi⊺x+b\begin{equation} \begin{aligned} f(\bm{x}) &= \bm{w}^\intercal \bm{x} + b \\ &= \sum_{i=1}^m \alpha_i y_i \bm{x}_i^\intercal \bm{x} + b \\ \end{aligned} \label{4} \end{equation}

KKT 条件为

{αi⩾0yif(xi)−1⩾0αi(yif(xi)−1)=0\left\lbrace\begin{aligned} &\alpha_i \ge 0 \\ &y_i f(\bm{x}_i) - 1 \ge 0 \\ &\alpha_i (y_i f(\bm{x}_i) - 1) = 0 \end{aligned}\right.

可以看出一定有 αi=0\alpha_i = 0 或 yif(xi)=1y_i f(\bm{x}_i) = 1。

  • 若 αi=0\alpha_i = 0，则该样本压根不会出现在模型当中，不会对 f(x)f(\bm{x}) 有任何影响。
  • 若 αi>0\alpha_i > 0，则一定有 yif(xi)=1y_i f(\bm{x}_i) = 1，即对应的样本点位于最大间隔边界上，是一个支持向量。

因此得到了支持向量机一个重要性质——解的稀疏性：训练完成后，大部分的训练样本都不需要保留，最终模型仅与支持向量有关。

SMO 算法

求解 (3)\eqref{3} 可以使用 SMO (Sequential Minimal Optimization) 算法。

基本思路：不断执行如下两个步骤直至收敛：

  1. 选取一对需更新的变量 αi,αj\alpha_i, \alpha_{j}
  2. 固定 αi,αj\alpha_i, \alpha_{j} 以外的参数，求解对偶问题更新 αi,αj\alpha_i, \alpha_{j}

仅考虑 αi,αj\alpha_i, \alpha_{j} 时，对偶问题的约束

0=∑i=1mαiyi0 = \sum_{i=1}^{m}\alpha_i y_i

变为

αiyi+αjyj=c,αi,αj⩾0\alpha_i y_i + \alpha_j y_j = c,\quad \alpha_i, \alpha_j \ge 0

其中 c=−∑k≠i,jαkykc = -\displaystyle \sum_{k \neq i, j} \alpha_k y_k 是使得约束条件成立的常数。

选取的 αi,αj\alpha_i, \alpha_{j} 有一个不满足 (3)\eqref{3} 时，目标函数就会在迭代后减小。直观来看，KKT 条件 (3)\eqref{3} 违背程度越大，变量更新后导致的目标函数值的减幅越大。因此 SMO 先选取违背 (3)\eqref{3} 程度最大的变量，第二个变量应选择一个使目标函数减小最快的变量。

不过这样比较各变量对应的目标函数减幅的复杂度过高，SMO 采用了一个启发式：使选取的两变量所对应样本之间的间隔最大。

一种直观的解释是，这样的两个变量有很大的差别，与对两个相似的变量进行更新相比，对它们进行更新会带给目标函数值更大的变化。

消去 (3)\eqref{3} 中的 αj\alpha_{j}，则得到一个关于 αi\alpha_i 的单变量二次规划问题，仅有的约束是 αi⩾0\alpha_i \ge 0，这样的二次规划问题有闭式解。

对于偏移项 bb，对任意支持向量 (xs,ys)(\bm{x}_s, y_s) 都有 ysf(xs)=1y_s f(\bm{x}_s) = 1，即

ys(∑i∈Sαiyixi⊺xs+b)=1y_s \left( \sum_{i \in S} \alpha_i y_i \bm{x}_i^\intercal \bm{x}_s + b \right) = 1

其中 S={i∣αi>0,i=1,2,…,m}S = \left\lbrace i \mid \alpha_i > 0, i = 1, 2, \dots, m \right\rbrace 为所有支持向量的下标集。

理论上可选取任意支持向量并通过上式获得 bb，但现实任务中常采用一种更鲁棒的做法，即使用所有支持向量求解的平均值

b=1∣S∣∑s∈S(ys−∑i∈Sαiyixi⊺xs)b = \frac{1}{\left| S \right|} \sum_{s \in S} \left( y_s - \sum_{i \in S} \alpha_i y_i \bm{x}_i^\intercal \bm{x}_s \right)

上式需要注意到 1ys=ys\dfrac{1}{y_s} = y_s。

核函数

前面的讨论中，假设了训练样本是线性可分的，即存在一个划分超平面能够将训练样本正确分类。但实际任务中，训练样本可能是线性不可分的。如下图的「异或问题」：

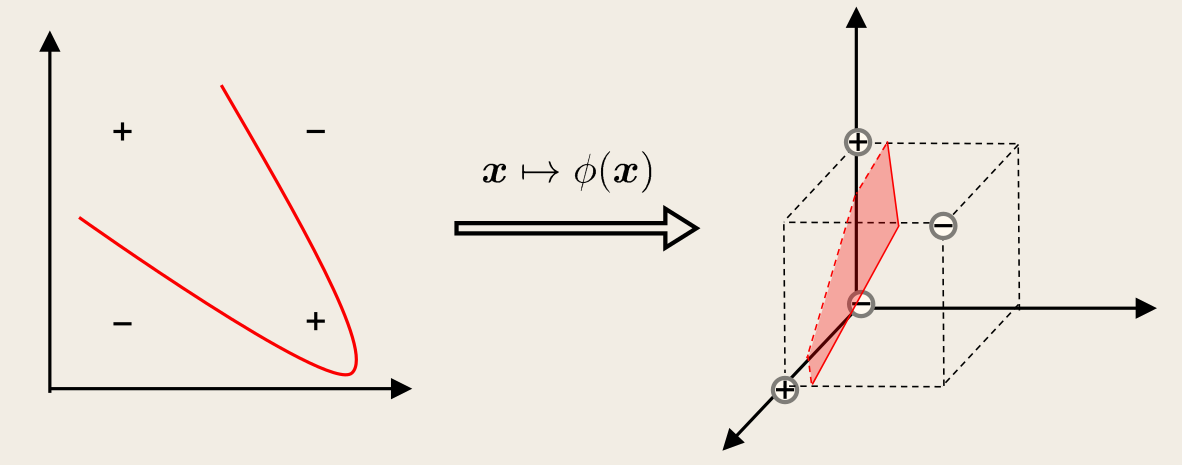
对这样的问题，可将样本从原始空间映射到一个更高维的特征空间，使得在这个特征空间中样本是线性可分的。

上图中，若将原始的二维空间映射到一个合适的三维空间，就能找到一个合适的划分超平面。

若原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本线性可分。

令 ϕ(x)\phi(\bm{x}) 表示将 x\bm{x} 映射后的特征向量，于是特征空间中划分超平面所对应的模型可表示为

f(x)=w⊺ϕ(x)+bf(\bm{x}) = \bm{w}^\intercal \phi(\bm{x}) + b

其中 w,b\bm{w}, b 是模型参数。

类似地有对偶问题

max⁡α∑i=1mαi−12∑i=1m∑j=1mαiαjyiyjϕ(xi)⊺ϕ(xj)s.t.∑i=1mαiyi=0, αi⩾0,i=1,2,…,m\begin{aligned} &\max_{\bm{\alpha}} \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \phi(\bm{x}_i)^\intercal \phi(\bm{x}_j) \\ &\text{s.t.} \quad \sum_{i=1}^{m}\alpha_i y_i = 0,\, \alpha_i \ge 0, \quad i = 1, 2, \dots, m \end{aligned}

求解上式涉及到计算 ϕ(xi)⊺ϕ(xj)\phi(\bm{x}_i)^\intercal \phi(\bm{x}_{j})，是样本 xi,xj\bm{x}_i, \bm{x}_{j} 映射到特征空间之后的内积。由于特征空间的维数可能很高，甚至是无穷维，因此直接计算是很困难的，需要避开这个障碍。

可以设想一个这样的函数

κ(xi,xj)=ϕ(xi)⊺ϕ(xj)\kappa(\bm{x}_i, \bm{x}_{j}) = \phi(\bm{x}_i)^\intercal \phi(\bm{x}_{j})

即 xi,xj\bm{x}_i, \bm{x}_{j} 在特征空间的内积等于它们在原始样本空间中通过函数 κ\kappa 计算的结果。于是可重写对偶问题为

max⁡α∑i=1mαi−12∑i=1m∑j=1mαiαjyiyjκ(xi,xj)s.t.∑i=1mαiyi=0, αi⩾0,i=1,2,…,m\begin{equation} \begin{aligned} &\max_{\bm{\alpha}} \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \kappa(\bm{x}_i, \bm{x}_j) \\ &\text{s.t.} \quad \sum_{i=1}^{m}\alpha_i y_i = 0,\, \alpha_i \ge 0, \quad i = 1, 2, \dots, m \end{aligned} \label{5} \end{equation}

求解后即可得到

f(x)=w⊺ϕ(x)+b=∑i=1mαiyiϕ(xi)⊺ϕ(x)+b=∑i=1mαiyiκ(x,xi)+b\begin{equation} \begin{aligned} f(\bm{x}) &= \bm{w}^\intercal \phi(\bm{x}) + b\\ &= \sum_{i=1}^{m} \alpha_i y_i \phi(\bm{x}_i)^\intercal \phi(\bm{x}) + b\\ &= \sum_{i=1}^{m} \alpha_i y_i \kappa(\bm{x}, \bm{x}_i) + b \end{aligned}\label{6} \end{equation}

这种方法称为核技巧（kernel trick），函数 κ\kappa 称为核函数（kernel function）。

(6)\eqref{6} 显示出模型最优解可通过训练样本的核函数展开，这一展式亦称为支持向量展式（support vector expansion）。

若已知映射 ϕ\phi 的具体形式，则可写出核函数 κ\kappa。但现实中通常不知道 ϕ\phi 的形式，核函数是否一定存在？什么样的函数能做核函数？

核函数定理

令 X\mathcal{X} 为输入空间，κ\kappa 是定义在 X×X\mathcal{X} \times \mathcal{X} 上的对称函数，则 κ\kappa 是核函数当且仅当对于任意数据集 D={x1,x2,…,xm}D = \left\lbrace \bm{x}_1, \bm{x}_2, \dots, \bm{x}_m \right\rbrace，「核矩阵」（kernel matrix）K=[κ(xi,xj)]m\bm{K} = [\kappa(\bm{x}_i, \bm{x}_{j})]_{m} 是半正定的。

也就是说，只要一个对称函数所对应的核矩阵半正定，就能作为核函数使用。实际上对于一个半正定矩阵，总能找到一个与之对应的映射 ϕ\phi。换言之，任意一个核函数都隐式地定义了一个称为「再生核希尔伯特空间」（reproducing kernel Hilbert space, RKHS）的特征空间。

特征空间的好坏对于支持向量机的性能至关重要，核函数的选择就成为了支持向量机的最大变数。

几种常用的核函数

名称 表达式 κ(xi,xj)\kappa(\bm{x}_i, \bm{x}_{j}) 参数
线性核 xi⊺xj\bm{x}_i^\intercal \bm{x}_{j} -
多项式核 (xi⊺xj)d(\bm{x}_i^\intercal \bm{x}_{j})^d d⩾1d \ge 1 为多项式的次数
高斯核（RBF 核） exp⁡(−∥xi−xj∥22σ2)\exp\left( -\frac{\left\lVert \bm{x}_i - \bm{x}_{j} \right\rVert^2}{2\sigma^2} \right) σ>0\sigma > 0 为高斯核的带宽（width）
拉普拉斯核 exp⁡(−∥xi−xj∥σ)\exp\left( -\frac{\left\lVert \bm{x}_i - \bm{x}_{j} \right\rVert}{\sigma} \right) σ>0\sigma > 0
Sigmoid 核 tanh⁡(βxi⊺xj+θ)\tanh(\beta \bm{x}_i^\intercal \bm{x}_{j} + \theta) β>0,θ<0\beta > 0, \theta < 0

还可以通过函数组合得到

  • 若 κ1,κ2\kappa_1, \kappa_2 是核函数，则对于任意正数 γ1,γ2\gamma_1, \gamma_2，其线性组合 γ1κ1+γ2κ2\gamma_1 \kappa_1 + \gamma_2 \kappa_2 也是核函数
  • 若 κ1,κ2\kappa_1, \kappa_2 是核函数，则它们的直积 κ1⊗κ2(x,z)=κ1(x,z)κ2(x,z)\kappa_1 \otimes \kappa_2(\bm{x}, \bm{z}) = \kappa_1(\bm{x}, \bm{z}) \kappa_2(\bm{x}, \bm{z}) 也是核函数
  • 若 κ1\kappa_1 是核函数，则对于任意函数 g(x)g(\bm{x})，κ(x,z)=g(x)κ1(x,z)g(z)\kappa(\bm{x}, \bm{z}) = g(\bm{x}) \kappa_1(\bm{x}, \bm{z}) g(\bm{z}) 也是核函数

软间隔与正则化

现实任务中，往往很难确定合适的核函数使得训练样本在特征空间中线性可分。即使找到了某个核函数，也很难断定是否是由于过拟合所造成的。

缓解该问题的一个办法是允许向量机在一些样本上出错，为此需要引入软间隔（soft margin）的概念，如下图所示：

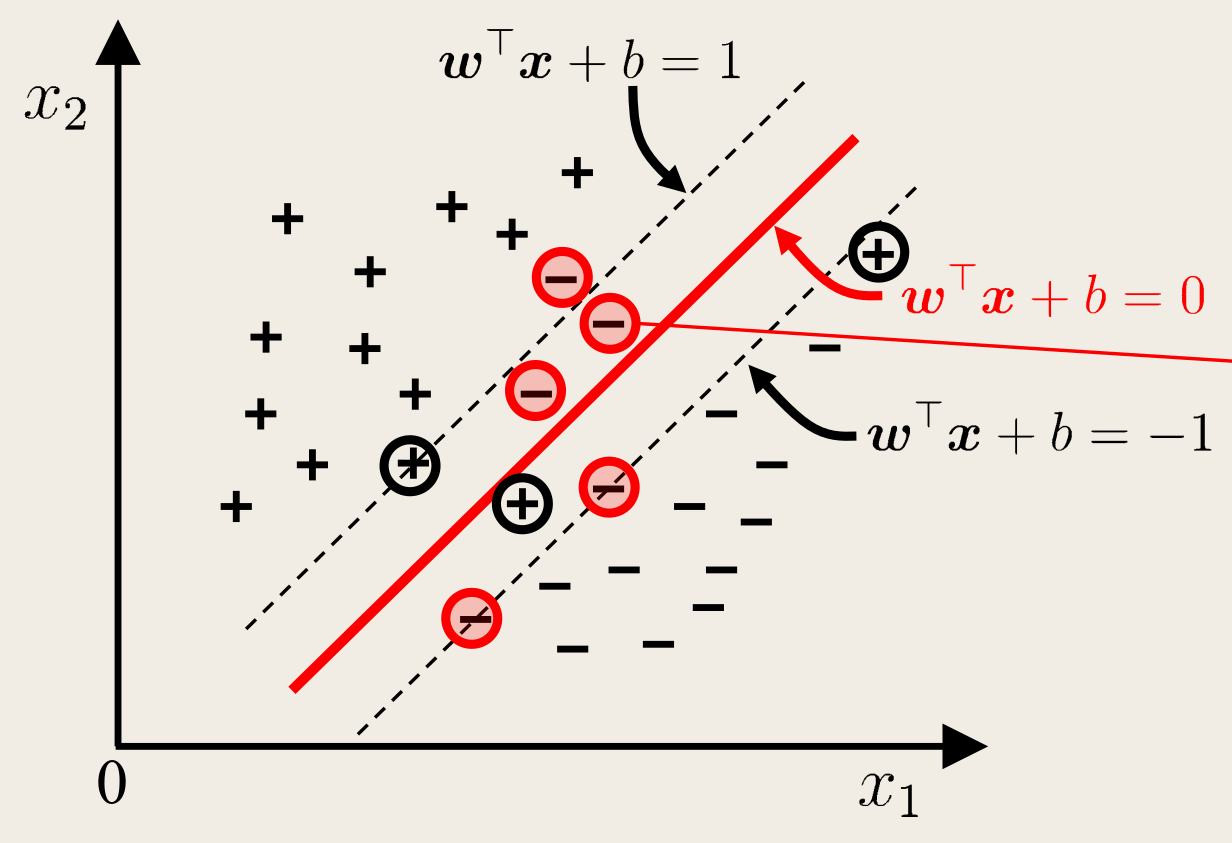
前面介绍的支持向量机形式要求所有样本满足约束 (1)\eqref{1}，即所有样本必须划分正确，这称为硬间隔（hard margin），而软间隔则允许某些样本不满足约束 (1)\eqref{1}。

但与此同时，最大化间隔的同时，不满足约束的样本应尽可能的少，于是优化目标可写为

min⁡w,b,ξ12∥w∥2+C∑i=1mℓ0/1(yi(w⊺xi+b)−1)\begin{equation} \min_{\bm{w}, b, \bm{\xi}} \frac{1}{2} \left\| \bm{w} \right\|^2 + C \sum_{i=1}^m \ell_{0 / 1} (y_i(\bm{w}^\intercal \bm{x}_i + b) - 1) \label{7} \end{equation}

其中 C>0C > 0 是一个常数，ℓ0/1\ell_{0 / 1} 是「0/1 损失函数」：

ℓ0/1(z){1,z<00,z⩾0\ell_{0 / 1}(z)\begin{cases} 1, & z < 0 \\ 0, & z \ge 0 \end{cases}

CC 为无穷大时，迫使所有样本满足约束，此时为硬间隔；CC 为有限值时，允许一些样本不满足约束，此时为软间隔。

然而 ℓ0/1\ell_{0 / 1} 数学性质不好，通常使用其他函数替代，称为替代损失（surrogate loss），例如

  • hinge 损失：ℓhinge(z)=max⁡(0,1−z)\ell_{\text{hinge}}(z) = \max(0, 1 - z)
  • 指数损失（exponential loss）：ℓexp(z)=exp⁡(−z)\ell_{\text{exp}}(z) = \exp(-z)
  • 对率损失（logistic loss）：ℓlog(z)=log⁡(1+exp⁡(−z))\ell_{\text{log}}(z) = \log(1 + \exp(-z))

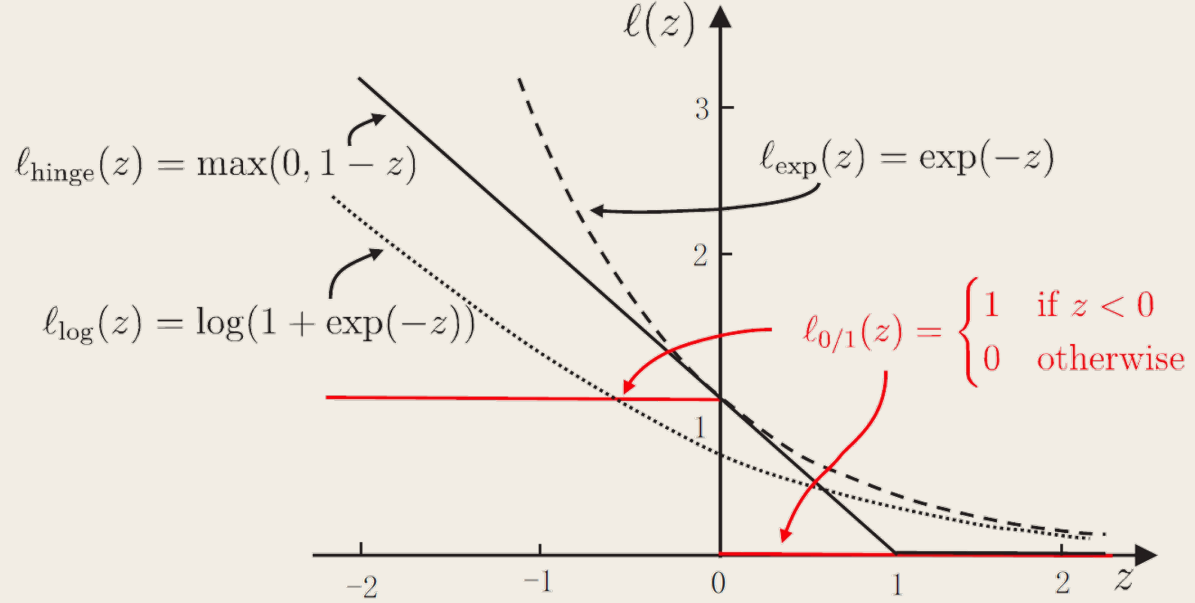
下面采用了 hinge 损失，虽然没有显式写出。而且 hinge 损失的 zz 取的是 yi(w⊺xi+b)y_i(\bm{w}^\intercal \bm{x}_i + b)。

引入松弛变量（slack variables）ξi⩾0\xi_i \ge 0，则 (7)\eqref{7} 可写为

min⁡w,b,ξ12∥w∥2+C∑i=1mξis.t.yi(w⊺xi+b)⩾1−ξi,ξi⩾0,i=1,2,…,m\begin{equation} \begin{aligned} &\min_{\bm{w}, b, \bm{\xi}} \frac{1}{2} \left\| \bm{w} \right\|^2 + C \sum_{i=1}^m \xi_i\\ &\text{s.t.} \quad y_i(\bm{w}^\intercal \bm{x}_i + b) \ge 1 - \xi_i, \quad \xi_i \ge 0, \quad i = 1, 2, \dots, m \end{aligned} \label{8} \end{equation}

这就是常用的「软间隔支持向量机」。

式 (8)\eqref{8} 每个样本都有一个对应的松弛变量，用以表征该样本不满足约束 (1)\eqref{1} 的程度。

类似 (2)\eqref{2}，这仍是一个二次规划问题，同样使用拉格朗日乘子法得到拉格朗日函数

L(w,b,α,ξ,μ)=12∥w∥2+C∑i=1mξi=+∑i=1mαi(1−ξi−yi(w⊺xi+b))−∑i=1mμiξi\begin{aligned} \mathcal{L}(\bm{w}, b, \bm{\alpha}, \bm{\xi}, \bm{\mu}) &= \dfrac{1}{2} \left\lVert \bm{w} \right\rVert^2 + C \sum_{i=1}^{m}\xi_i\\ &\phantom{=} + \sum_{i=1}^{m}\alpha_i(1 - \xi_i - y_i(\bm{w}^\intercal \bm{x}_i + b)) - \sum_{i=1}^{m}\mu_i \xi_i \end{aligned}

其中 αi,μi⩾0\alpha_i, \mu_i \ge 0 是拉格朗日乘子。

对 w,b,ξi\bm{w}, b, \xi_i 求偏导数为零，得

{w=∑i=1mαiyixi0=∑i=1mαiyiC=αi+μi\left\lbrace\begin{aligned} \bm{w} &= \sum_{i=1}^{m}\alpha_i y_i \bm{x}_i \\ 0 &= \sum_{i=1}^{m}\alpha_i y_i \\ C &= \alpha_i + \mu_i \end{aligned}\right.

将上面三个式子代入拉格朗日函数可得对偶问题

max⁡α∑i=1mαi−12∑i=1m∑j=1mαiαjyiyjxi⊺xjs.t.∑i=1mαiyi=0, 0⩽αi⩽C,i=1,2,…,m\begin{equation} \begin{aligned} &\max_{\bm{\alpha}} \sum_{i=1}^{m}\alpha_i - \dfrac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_j y_i y_j \bm{x}_i^\intercal \bm{x}_j\\ &\text{s.t.} \quad \sum_{i=1}^{m}\alpha_i y_i = 0,\, 0 \le \alpha_i \le C, \quad i = 1, 2, \dots, m \end{aligned} \label{9} \end{equation}

对照原对偶问题，二者唯一的差别是对于对偶变量的约束不同：原问题是 0⩽αi0 \le \alpha_i，而这里是 0⩽αi⩽C0 \le \alpha_i \le C。于是可以采用同样的算法求解 (9)\eqref{9}。引入核函数后能得到与式 (6)\eqref{6} 相同的支持向量展式。

类似的，对软间隔支持向量机，KKT 条件要求

{αi,μi⩾0yif(xi)−1+ξi⩾0αi(yif(xi)−1+ξi)=0ξi⩾0, μiξi=0\left\lbrace\begin{aligned} &\alpha_i, \mu_i \ge 0\\ &y_i f(\bm{x}_i) - 1 + \xi_i \ge 0\\ &\alpha_i (y_i f(\bm{x}_i) - 1 + \xi_i) = 0\\ &\xi_i \ge 0,\, \mu_i \xi_i = 0 \end{aligned}\right.

于是对于任意训练样本 (xi,yi)(\bm{x}_i, y_i)，总有 αi=0\alpha_i = 0 或 yif(xi)=1−ξiy_i f(\bm{x}_i) = 1 - \xi_i。

  • 若 αi=0\alpha_i = 0，则该样本不会对 f(x)f(\bm{x}) 有任何影响。
  • 若 αi>0\alpha_i > 0，则必有 yif(xi)=1−ξiy_i f(\bm{x}_i) = 1 - \xi_i，即该样本是支持向量：
    • 若 αi<C\alpha_i < C，由上面的偏导结果有 μi>0\mu_i > 0，进而 ξi=0\xi_i = 0，即此时该样本恰在最大间隔边界上。
    • 若 αi=C\alpha_i = C，则有 μi=0\mu_i = 0，此时：
      • 若 ξi⩽1\xi_i \le 1，则该样本落在最大间隔内部。
      • 若 ξi>1\xi_i > 1，则该样本被错误分类。

由此可得，软间隔支持向量机最终模型仅与支持向量有关，即通过 hinge 损失函数仍保持了稀疏性。

将 (7)\eqref{7} 的 0/1 损失函数换成别的替代损失函数以得到其他学习模型，这些模型的性质与所用的替代函数直接相关。

但是这些模型都有一个共性：优化目标中的第一项用来描述划分超平面的「间隔大小」，另一项用来表述训练集上的误差，可写为更一般的形式

min⁡fΩ(f)+C∑i=1mℓ(f(xi),yi)\min_f \textcolor{ff0099}{\Omega(f)} + C \textcolor{05aa94}{\sum_{i=1}^{m} \ell(f(\bm{x}_i), y_i)}

  • 红色部分，即 Ω(f)\Omega(f) 称为结构风险（structural risk），用以描述模型 ff 的某些性质
  • 青色部分，即 ∑i=1mℓ(f(xi),yi)\displaystyle \sum_{i=1}^m\ell(f(\bm{x}_i), y_i) 称为经验风险（empirical risk），用以描述模型与训练数据的契合程度。

正则化可理解为「罚函数法」——通过对不希望的结果施以惩罚，使得优化过程趋于希望目标。

从这个角度，Ω(f)\Omega(f) 称为正则化项，CC 称为正则化常数。Lp\mathrm{L}_p 范数（norm）是常用的正则化项，其中 L2\mathrm{L}_2 范数 ∥w∥2\left\lVert \bm{w} \right\rVert_2 倾向于 w\bm{w} 的分量取值尽量均衡，即非零分量个数尽量稠密；而 L0\mathrm{L}_0 范数 ∥w∥0\left\lVert \bm{w} \right\rVert_0 和 L1\mathrm{L}_1 范数 ∥w∥1\left\lVert \bm{w} \right\rVert_1 则倾向于 w\bm{w} 的分量取值尽量稀疏，即非零分量个数尽量少。

从贝叶斯估计的角度，可认为是提供了模型的先验概率。

支持向量回归

现在考虑回归问题。给定训练样本 D={(xi,yi)}i=1m, yi∈RD = \left\lbrace (\bm{x}_i, y_i) \right\rbrace_{i=1}^m,\, y_i \in \R，希望学得一个形如 f(x)=w⊺x+bf(\bm{x}) = \bm{w}^\intercal \bm{x} + b 的回归模型，使得 f(x)f(\bm{x}) 与 yy 尽可能接近。而 w,b\bm{w}, b 是待确定的模型参数。

对样本 (x,y)(\bm{x}, y)，传统回归模型通常直接基于模型输出 f(x)f(\bm{x}) 与真实输出 yy 之间的差别来计算损失，当且仅当 f(x)=yf(\bm{x}) = y 时损失才为零。

支持向量回归（Support Vector Regression, SVR）则假设我们能「容忍」f(x)f(\bm{x}) 与 yy 之间最多有 ϵ\epsilon 的偏差，即当 ∣f(x)−y∣⩾ϵ\left| f(\bm{x}) - y \right| \ge \epsilon 时才计算损失。

这就相当于以 f(x)f(\bm{x}) 为中心，构建了一个宽度为 2ϵ2\epsilon 的间隔带，若训练样本落入此间隔带，则认为是被预测正确的：

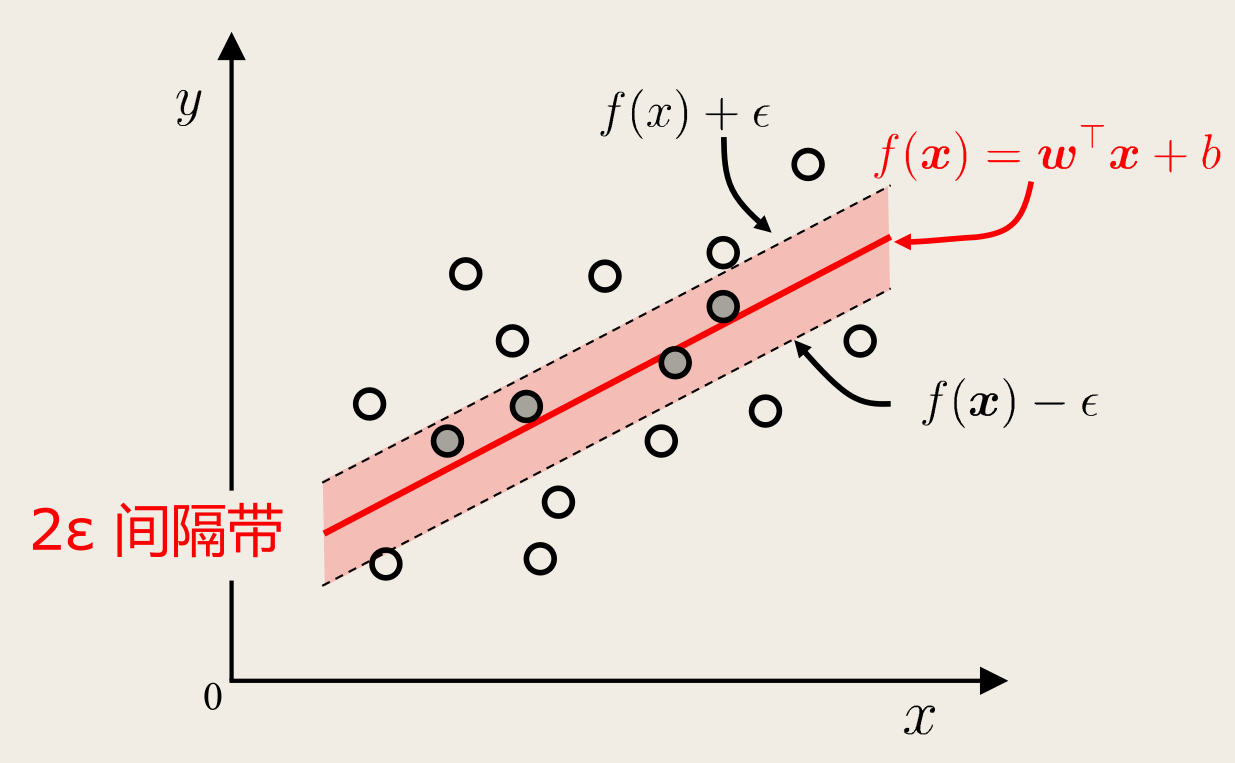
于是 SVR 问题可形式化为

min⁡w,b12∥w∥2+C∑i=1mℓϵ(f(xi)−yi)\begin{equation} \min_{\bm{w}, b} \frac{1}{2} \left\lVert \bm{w} \right\rVert^2 + C \sum_{i=1}^{m}\ell_{\epsilon}(f(\bm{x}_i) - y_i) \label{10} \end{equation}

其中 CC 为正则化常数，ℓϵ\ell_{\epsilon} 是 ϵ\epsilon-不敏感损失（ϵ\epsilon-insensitive loss）函数：

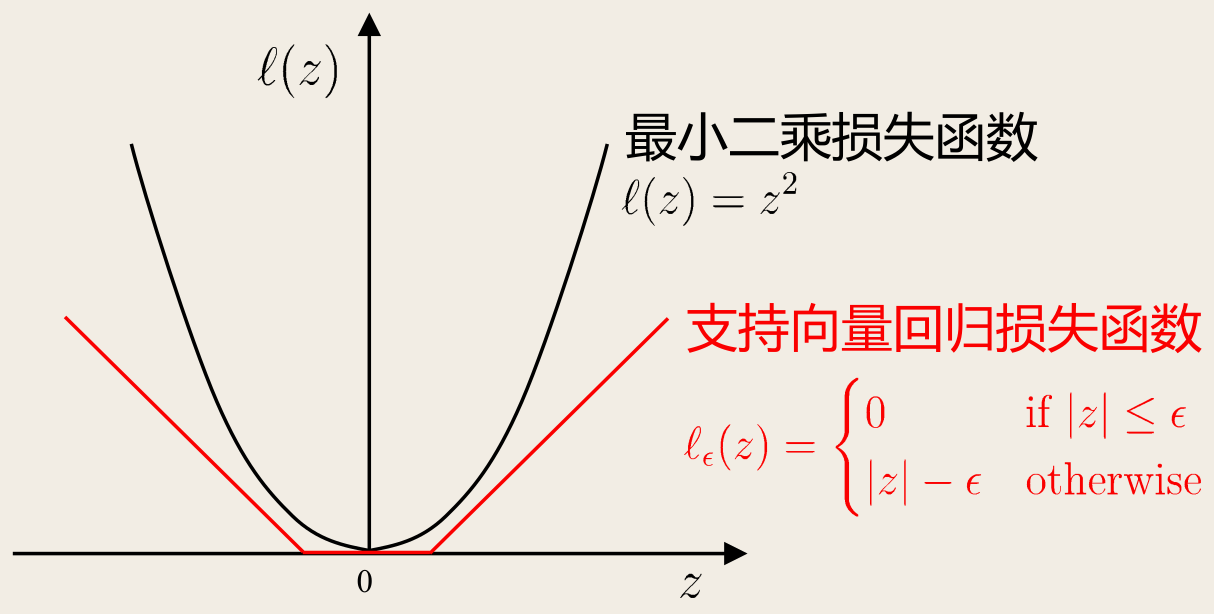
ℓϵ(z){0,∣z∣⩽ϵ∣z∣−ϵ,∣z∣>ϵ\ell_{\epsilon}(z)\begin{cases} 0, & \left| z \right| \le \epsilon \\ \left| z \right| - \epsilon, & \left| z \right| > \epsilon \end{cases}

引入松弛变量 ξi,ξ^i\xi_i, \hat{\xi}_i，则 (10)\eqref{10} 可写为

min⁡w,b,ξi,ξ^i12∥w∥2+C∑i=1m(ξi+ξ^i)s.t.f(xi)−yi⩽ϵ+ξi,yi−f(xi)⩽ϵ+ξ^i,ξi,ξ^i⩾0\begin{equation} \begin{aligned} &\min_{\bm{w}, b, \xi_i, \hat{\xi}_i} \frac{1}{2} \left\lVert \bm{w} \right\rVert^2 + C \sum_{i=1}^{m}(\xi_i + \hat{\xi}_i)\\ &\text{s.t.}\quad f(\bm{x}_i) - y_i \le \epsilon + \xi_i, \quad y_i - f(\bm{x}_i) \le \epsilon + \hat{\xi}_i, \quad \xi_i, \hat{\xi}_i \ge 0 \end{aligned} \label{11} \end{equation}

引入拉格朗日乘子 μi,μ^i,αi,α^i⩾0\mu_i, \hat{\mu}_i, \alpha_i, \hat{\alpha}_i \ge 0，拉格朗日函数

L(w,b,α,α^,ξ,ξ^,μ,μ^)=12∥w∥2+C∑i=1m(ξi+ξ^i)−∑i=1mμiξi−∑i=1mμ^iξ^i=+∑i=1mαi(f(xi)−yi−ϵ−ξi)+∑i=1mα^i(yi−f(xi)−ϵ−ξ^i)\begin{aligned} \mathcal{L}(\bm{w}, b, \bm{\alpha}, \hat{\bm{\alpha}}, \bm{\xi}, \hat{\bm{\xi}}, \bm{\mu}, \hat{\bm{\mu}}) &= \dfrac{1}{2}\left\lVert \bm{w} \right\rVert^2 + C\sum_{i=1}^{m}(\xi_i + \hat{\xi}_i) - \sum_{i=1}^{m}\mu_i\xi_i - \sum_{i=1}^{m}\hat{\mu}_i\hat{\xi}_i\\ &\phantom{=} + \sum_{i=1}^{m}\alpha_i(f(\bm{x}_i) - y_i - \epsilon - \xi_i) + \sum_{i=1}^{m}\hat{\alpha}_i(y_i - f(\bm{x}_i) - \epsilon - \hat{\xi}_i) \end{aligned}

对 w,b,ξi,ξ^i\bm{w}, b, \xi_i, \hat{\xi}_i 求偏导数为零，得

{w=∑i=1m(α^i−αi)xi0=∑i=1m(α^i−αi)C=αi+μiC=α^i+μ^i\left\lbrace\begin{aligned} \bm{w} &= \sum_{i=1}^{m}(\hat{\alpha}_i - \alpha_i)\bm{x}_i \\ 0 &= \sum_{i=1}^{m}(\hat{\alpha}_i - \alpha_i) \\ C &= \alpha_i + \mu_i\\ C &= \hat{\alpha}_i + \hat{\mu}_i \end{aligned}\right.

将上面四个式子代入拉格朗日函数可得对偶问题

max⁡α,α^∑i=1m[yi(α^i−αi)−ϵ(α^i+αi)]−12∑i=1m∑j=1m(α^i−αi)(α^j−αj)xi⊺xjs.t.∑i=1m(α^i−αi)=0, 0⩽αi,α^i⩽C,i=1,2,…,m\begin{equation} \begin{aligned} &\max_{\bm{\alpha}, \hat{\bm{\alpha}}} \sum_{i=1}^{m}[y_i(\hat{\alpha}_i - \alpha_i) - \epsilon(\hat{\alpha}_i + \alpha_i)] - \dfrac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}(\hat{\alpha}_i - \alpha_i)(\hat{\alpha}_j - \alpha_j)\bm{x}_i^\intercal \bm{x}_j\\ &\text{s.t.} \quad \sum_{i=1}^{m}(\hat{\alpha}_i - \alpha_i) = 0,\, 0 \le \alpha_i, \hat{\alpha}_i \le C, \quad i = 1, 2, \dots, m \end{aligned} \label{12} \end{equation}

KKT 条件为

{αi(f(xi)−yi−ϵ−ξi)=0α^i(yi−f(xi)−ϵ−ξ^i)=0αiα^i=0, ξiξ^i=0(C−αi)ξi=0, (C−α^i)ξ^i=0\left\lbrace\begin{aligned} &\alpha_i (f(\bm{x}_i) - y_i - \epsilon - \xi_i) = 0\\ &\hat{\alpha}_i (y_i - f(\bm{x}_i) - \epsilon - \hat{\xi}_i) = 0\\ &\alpha_i \hat{\alpha}_i = 0,\, \xi_i \hat{\xi}_i = 0\\ &(C - \alpha_i)\xi_i = 0,\, (C - \hat{\alpha}_i)\hat{\xi}_i = 0 \end{aligned}\right.

当且仅当 f(xi)−yi−ϵ−ξi=0f(\bm{x}_i) - y_i - \epsilon - \xi_i = 0 时 αi\alpha_i 能取非零值，当且仅当 yi−f(xi)−ϵ−ξ^i=0y_i - f(\bm{x}_i) - \epsilon - \hat{\xi}_i = 0 时 α^i\hat{\alpha}_i 能取非零值。

换言之，仅当样本 (xi,yi)(\bm{x}_i, y_i) 不落入 ϵ\epsilon-间隔带中，相应的 αi,α^i\alpha_i, \hat{\alpha}_i 才能取非零值。

此外，上述两个约束不能同时成立，因为 α,α^i\alpha, \hat{\alpha}_i 中至少一个为零。

代入 f(x)=w⊺x+bf(\bm{x}) = \bm{w}^\intercal \bm{x} + b，SVR 的解形如

f(x)=∑i=1m(α^i−αi)xi⊺x+b\begin{equation} f(\bm{x}) = \sum_{i=1}^{m}(\hat{\alpha}_i - \alpha_i)\bm{x}_i^\intercal \bm{x} + b \label{13} \end{equation}

能使 (13)\eqref{13} 中 (α^i−αi)≠0(\hat{\alpha}_i - \alpha_i) \ne 0 的样本即为 SVR 的支持向量，它们必落在 ϵ\epsilon-间隔带之外。

SVR 的支持向量仅是训练样本的一部分，即其解仍具有稀疏性。

由 KKT 条件可得，对每个样本 (xi,yi)(\bm{x}_i, y_i) 都有 (C−αi)ξi=0(C - \alpha_i) \xi_i = 0 与 αi(f(xi)−yi−ϵ−ξi)=0\alpha_i(f(\bm{x}_i) - y_i - \epsilon - \xi_i) = 0。于是得到 αi\alpha_i 后，若 0<αi<C0 < \alpha_i < C，则有 ξi=0\xi_i = 0，进而有

b=yi+ϵ−∑i=1m(α^i−αi)xi⊺xb = y_i + \epsilon - \sum_{i=1}^{m} (\hat{\alpha}_i - \alpha_i) \bm{x}_i^\intercal \bm{x}

因此求解 (12)\eqref{12} 得到 αi\alpha_i 后，可任意选取满足 0<αi<C0 < \alpha_i < C 的样本，通过上式求得 bb。实践中常采用一种更鲁棒的方法，选取多个（或所有）满足条件 0<αi<C0 < \alpha_i < C 的样本求解 bb 后取平均值。

考虑特征映射形式 f(x)=w⊺ϕ(x)+bf(\bm{x}) = \bm{w}^\intercal \phi(\bm{x}) + b，则上面的 w=∑i=1m(α^i−αi)xi\bm{w} = \sum_{i=1}^{m} (\hat{\alpha}_i - \alpha_i) \bm{x}_i 将形如

w=∑i=1m(α^i−αi)ϕ(xi)\bm{w} = \sum_{i=1}^{m} (\hat{\alpha}_i - \alpha_i) \phi(\bm{x}_i)

则 SVR 的解可表示为

f(x)=∑i=1m(α^i−αi)κ(x,xi)+bf(\bm{x}) = \sum_{i=1}^{m} (\hat{\alpha}_i - \alpha_i) \kappa(\bm{x}, \bm{x}_i) + b

其中 κ(x,xi)=ϕ(x)⊺ϕ(xi)\kappa(\bm{x}, \bm{x}_i) = \phi(\bm{x})^\intercal \phi(\bm{x}_i) 是核函数。

核方法

给定训练样本 {(xi,yi)}i=1m\left\lbrace (\bm{x}_i, y_i) \right\rbrace_{i=1}^m，若不考虑偏移项 bb，无论是 SVM 还是 SVR，学得模型总能表示为核函数 κ(x,xi)\kappa(\bm{x}, \bm{x}_i) 的线性组合。

表示定理（Representer 定理）

令 H\mathbb{H} 为核函数 κ\kappa 对应的再生核希尔伯特空间，∥h∥H\left\lVert h \right\rVert_{\mathbb{H}} 表示 H\mathbb{H} 空间中关于 hh 的范数，对于任意单调递增函数 Ω ⁣:[0,∞]→R\Omega\colon [0, \infty ] \to \R 和任意非负损失函数 ℓ ⁣:Rm→[0,∞]\ell\colon \R^m \to [0, \infty ]，优化问题

min⁡h∈HF(h)=Ω(∥h∥H)+ℓ(h(x1),…,h(xm))\min_{h \in \mathbb{H}} F(h) = \Omega(\left\lVert h \right\rVert_{\mathbb{H}}) + \ell(h(\bm{x}_1), \dots, h(\bm{x}_m))

的解总能表示为

h∗(x)=∑i=1mαiκ(x,xi)h^{*}(\bm{x}) = \sum_{i=1}^{m}\alpha_i \kappa(\bm{x}, \bm{x}_i)

表示定理对于损失函数没有限制，对正则化项 Ω\Omega 仅要求单调递增，甚至不要求 Ω\Omega 是凸函数。因此对于一般的损失函数和正则化项，上面的优化问题的解都能表示为核函数的线性组合。

人们发展出一系列基于核函数的学习方法，统称为「核方法」（kernel methods）。最常见的是通过「核化」（即引入核函数）来将线性学习器拓展为非线性学习器。

具体略。