聚类任务
「无监督学习」学习任务中,聚类 (clustering)是研究最多、应用最广的。
「聚类」对应有监督学习中的「分类」任务。无监督学习任务还有「密度估计」,对应有监督学习中的「回归」任务。
聚类是将数据集中的样本划分为若干个不相交的子集,每个子集称为一个簇 (cluster)。簇内的样本尽可能相似,而簇间的样本尽可能不同。
形式化地描述,假定样本集 D = { x i } i = 1 m D = \left\lbrace \bm{x}_i \right\rbrace_{i=1}^m D = { x i } i = 1 m m m m x i = ( x i 1 ; x i 2 ; ⋯ ; x i n ) \bm{x}_i = \left( x_{i1}; x_{i2}; \cdots; x_{in} \right) x i = ( x i 1 ; x i 2 ; ⋯ ; x in ) n n n D D D k k k { C l } l = 1 k \left\lbrace C_l \right\rbrace_{l=1}^k { C l } l = 1 k C l C_l C l l l l C l ∩ l ≠ l ′ C l ′ = ∅ C_l \cap_{l \ne l'} C_{l'} = \empty C l ∩ l = l ′ C l ′ = ∅ D = ⋃ l = 1 k C l D = \bigcup_{l=1}^k C_l D = ⋃ l = 1 k C l
相应地,用 λ j ∈ { 1 , 2 , ⋯ , k } \lambda_{j} \in \left\lbrace 1, 2, \cdots, k \right\rbrace λ j ∈ { 1 , 2 , ⋯ , k } x j \bm{x}_j x j x j ∈ C λ j \bm{x}_j \in C_{\lambda_j} x j ∈ C λ j m m m λ = ( λ 1 ; λ 2 ; ⋯ ; λ m ) \bm{\lambda} = \left( \lambda_1; \lambda_2; \cdots; \lambda_m \right) λ = ( λ 1 ; λ 2 ; ⋯ ; λ m )
性能度量
「聚类性能度量」,亦称聚类「有效性指标」(validity index),与监督学习中的性能度量作用相似。
直观上我们想要「物以类聚」,即同一簇的样本尽可能相似,不同簇的样本尽可能不同。换言之,聚类结果的「簇内相似度」(intra-cluster similarity)应高,而「簇间相似度」(inter-cluster similarity)应低。
聚类性能度量大致有两类:
外部指标 :将聚类结果与某个「参考模型」(ground truth)进行比较
如 Jaccard 系数、FM 指数、Rand 指数等。
内部指标 :直接考察聚类结果而不利用任何参考模型
外部指标
对数据集 D = { x i } i = 1 m D = \left\lbrace \bm{x}_i \right\rbrace_{i=1}^m D = { x i } i = 1 m C = { C 1 , ⋯ , C k } \mathcal{C} = \left\lbrace C_1, \cdots, C_k \right\rbrace C = { C 1 , ⋯ , C k } C ∗ = { C 1 ∗ , ⋯ , C s ∗ } \mathcal{C}^* = \left\lbrace C_1^*, \cdots, C_s^* \right\rbrace C ∗ = { C 1 ∗ , ⋯ , C s ∗ } λ , λ ∗ \bm{\lambda}, \bm{\lambda}^* λ , λ ∗
我们将样本两两配对考虑,定义
{ a = ∣ S S ∣ , S S = { ( x i , x j ) ∣ λ i = λ j , λ i ∗ = λ j ∗ , i < j } , b = ∣ S D ∣ , S D = { ( x i , x j ) ∣ λ i = λ j , λ i ∗ ≠ λ j ∗ , i < j } , c = ∣ D S ∣ , D S = { ( x i , x j ) ∣ λ i ≠ λ j , λ i ∗ = λ j ∗ , i < j } , d = ∣ D D ∣ , D D = { ( x i , x j ) ∣ λ i ≠ λ j , λ i ∗ ≠ λ j ∗ , i < j } . \left\lbrace\begin{aligned}
a &= |SS|,\quad SS = \left\lbrace (\bm{x}_i, \bm{x}_j) \mid \lambda_i = \lambda_j, \lambda_i^* = \lambda_j^* , i < j\right\rbrace,\\
b &= |SD|,\quad SD = \left\lbrace (\bm{x}_i, \bm{x}_j) \mid \lambda_i = \lambda_j, \lambda_i^* \ne \lambda_j^* , i < j\right\rbrace,\\
c &= |DS|,\quad DS = \left\lbrace (\bm{x}_i, \bm{x}_j) \mid \lambda_i \ne \lambda_j, \lambda_i^* = \lambda_j^* , i < j\right\rbrace,\\
d &= |DD|,\quad DD = \left\lbrace (\bm{x}_i, \bm{x}_j) \mid \lambda_i \ne \lambda_j, \lambda_i^* \ne \lambda_j^* , i < j\right\rbrace.
\end{aligned}\right.
⎩ ⎨ ⎧ a b c d = ∣ S S ∣ , S S = { ( x i , x j ) ∣ λ i = λ j , λ i ∗ = λ j ∗ , i < j } , = ∣ S D ∣ , S D = { ( x i , x j ) ∣ λ i = λ j , λ i ∗ = λ j ∗ , i < j } , = ∣ D S ∣ , D S = { ( x i , x j ) ∣ λ i = λ j , λ i ∗ = λ j ∗ , i < j } , = ∣ D D ∣ , D D = { ( x i , x j ) ∣ λ i = λ j , λ i ∗ = λ j ∗ , i < j } .
S S S D D D
基于上面,可导出常用的聚类性能度量外部指标:
Jaccard 系数(Jaccard coefficient, JC):J C = a a + b + c \mathrm{JC} = \frac{a}{a+b+c}
JC = a + b + c a
FM 指数(Fowlkes and Mallows index, FMI):F M I = a a + b ⋅ a a + c \mathrm{FMI} = \sqrt{\frac{a}{a+b} \cdot \frac{a}{a+c}}
FMI = a + b a ⋅ a + c a
Rand 指数(Rand index, RI):R I = a + d ( m 2 ) = 2 ( a + d ) m ( m − 1 ) \mathrm{RI} = \dfrac{a+d}{\binom{m}{2}} = \dfrac{2(a+d)}{m(m-1)}
RI = ( 2 m ) a + d = m ( m − 1 ) 2 ( a + d )
这些指标的取值范围都是 [ 0 , 1 ] [0, 1] [ 0 , 1 ]
内部指标
考虑聚类结果的簇划分 C = { C 1 , ⋯ , C k } \mathcal{C} = \left\lbrace C_1, \cdots, C_k \right\rbrace C = { C 1 , ⋯ , C k }
{ d a v g ( C ) = 1 ( ∣ C ∣ 2 ) ∑ 1 ⩽ i < j ⩽ ∣ C ∣ dist ( x i , x j ) , diam ( C ) = max 1 ⩽ i , j ⩽ ∣ C ∣ dist ( x i , x j ) , d min ( C i , C j ) = min x i ∈ C i , x j ∈ C j dist ( x i , x j ) , d c e n ( C i , C j ) = dist ( μ i , μ j ) . \left\lbrace\begin{aligned}
d_{\mathrm{avg}}(C) &= \dfrac{1}{\binom{|C|}{2}} \sum_{1 \le i < j \le |C|} \operatorname{dist}(\bm{x}_i, \bm{x}_j),\\
\operatorname{diam}(C) &= \max_{1 \le i, j \le |C|} \operatorname{dist}(\bm{x}_i, \bm{x}_j),\\
d_{\min}(C_i, C_j) &= \min_{\bm{x}_i \in C_i, \bm{x}_j \in C_j} \operatorname{dist}(\bm{x}_i, \bm{x}_j),\\
d_{\mathrm{cen}}(C_i, C_j) &= \operatorname{dist}(\bm{\mu}_i, \bm{\mu}_j).
\end{aligned}\right.
⎩ ⎨ ⎧ d avg ( C ) diam ( C ) d m i n ( C i , C j ) d cen ( C i , C j ) = ( 2 ∣ C ∣ ) 1 1 ⩽ i < j ⩽ ∣ C ∣ ∑ dist ( x i , x j ) , = 1 ⩽ i , j ⩽ ∣ C ∣ max dist ( x i , x j ) , = x i ∈ C i , x j ∈ C j min dist ( x i , x j ) , = dist ( μ i , μ j ) .
d a v g ( C ) d_{\mathrm{avg}}(C) d avg ( C ) C C C diam ( C ) \operatorname{diam}(C) diam ( C ) C C C d min ( C i , C j ) d_{\min}(C_i, C_j) d m i n ( C i , C j ) C i C_i C i C j C_j C j d c e n ( C i , C j ) d_{\mathrm{cen}}(C_i, C_j) d cen ( C i , C j ) C i C_i C i C j C_j C j
基于上面,可导出常用的聚类性能度量内部指标:
DB 指数(Davies-Bouldin index, DBI):D B I = 1 k ∑ i = 1 k max j ≠ i ( d a v g ( C i ) + d a v g ( C j ) d c e n ( C i , C j ) ) \mathrm{DBI} = \dfrac{1}{k} \sum_{i=1}^k \max_{j \ne i} \left( \dfrac{d_{\mathrm{avg}}(C_i) + d_{\mathrm{avg}}(C_j)}{d_{\mathrm{cen}}(C_i, C_j)} \right)
DBI = k 1 i = 1 ∑ k j = i max ( d cen ( C i , C j ) d avg ( C i ) + d avg ( C j ) )
Dunn 指数(Dunn index, DI):D I = min 1 ⩽ i ⩽ k { min j ≠ i ( d min ( C i , C j ) max 1 ⩽ l ⩽ k diam ( C l ) ) } \mathrm{DI} = \min_{1 \le i \le k} \left\lbrace \min_{j \ne i} \left( \dfrac{d_{\min}(C_i, C_j)}{\max\limits_{1\le l\le k} \operatorname{diam}(C_l)} \right) \right\rbrace
DI = 1 ⩽ i ⩽ k min ⎩ ⎨ ⎧ j = i min 1 ⩽ l ⩽ k max diam ( C l ) d m i n ( C i , C j ) ⎭ ⎬ ⎫
距离计算
函数 dist \operatorname{dist} dist
非负性:dist ( x i , x j ) ⩾ 0 \operatorname{dist}(\bm{x}_i, \bm{x}_j) \ge 0 dist ( x i , x j ) ⩾ 0
同一性:dist ( x i , x j ) = 0 ⟺ x i = x j \operatorname{dist}(\bm{x}_i, \bm{x}_j) = 0 \iff \bm{x}_i = \bm{x}_j dist ( x i , x j ) = 0 ⟺ x i = x j
对称性:dist ( x i , x j ) = dist ( x j , x i ) \operatorname{dist}(\bm{x}_i, \bm{x}_j) = \operatorname{dist}(\bm{x}_j, \bm{x}_i) dist ( x i , x j ) = dist ( x j , x i )
直递性:dist ( x i , x j ) ⩽ dist ( x i , x k ) + dist ( x k , x j ) \operatorname{dist}(\bm{x}_i, \bm{x}_j) \le \operatorname{dist}(\bm{x}_i, \bm{x}_k) + \operatorname{dist}(\bm{x}_k, \bm{x}_j) dist ( x i , x j ) ⩽ dist ( x i , x k ) + dist ( x k , x j )
给定样本 x i = ( x i 1 ; ⋯ ; x i n ) , x j = ( x j 1 ; ⋯ ; x j n ) \bm{x}_i = (x_{i1}; \cdots; x_{in}),\, \bm{x}_j = (x_{j1}; \cdots; x_{jn}) x i = ( x i 1 ; ⋯ ; x in ) , x j = ( x j 1 ; ⋯ ; x j n ) 闵可夫斯基距离 (Minkowski distance):
dist m k ( x i , x j ) = ( ∑ u = 1 n ∣ x i u − x j u ∣ p ) 1 p \operatorname{dist}_{\mathrm{mk}}(\bm{x}_i, \bm{x}_j) = \left( \sum_{u=1}^n |x_{iu} - x_{ju}|^p \right)^{\frac{1}{p}}
dist mk ( x i , x j ) = ( u = 1 ∑ n ∣ x i u − x j u ∣ p ) p 1
其中 p ⩾ 1 p \ge 1 p ⩾ 1
也可以写为 x i − x j \bm{x}_i - \bm{x}_{j} x i − x j L p \mathrm{L}_p L p ∥ x i − x j ∥ p \left\lVert \bm{x}_i - \bm{x}_{j} \right\rVert_p ∥ x i − x j ∥ p
特别地,有
欧氏距离(Euclidean distance):p = 2 p=2 p = 2 dist e u ( x i , x j ) = ∥ x i − x j ∥ 2 = ∑ u = 1 n ( x i u − x j u ) 2 \operatorname{dist}_{\mathrm{eu}}(\bm{x}_i, \bm{x}_j) = \left\lVert \bm{x}_i - \bm{x}_{j} \right\rVert_2 = \sqrt{\sum_{u=1}^n (x_{iu} - x_{ju})^2}
dist eu ( x i , x j ) = ∥ x i − x j ∥ 2 = u = 1 ∑ n ( x i u − x j u ) 2
曼哈顿距离(Manhattan distance):p = 1 p=1 p = 1 dist m a ( x i , x j ) = ∥ x i − x j ∥ 1 = ∑ u = 1 n ∣ x i u − x j u ∣ \operatorname{dist}_{\mathrm{ma}}(\bm{x}_i, \bm{x}_j) = \left\lVert \bm{x}_i - \bm{x}_{j} \right\rVert_1 = \sum_{u=1}^n |x_{iu} - x_{ju}|
dist ma ( x i , x j ) = ∥ x i − x j ∥ 1 = u = 1 ∑ n ∣ x i u − x j u ∣
切比雪夫距离(Chebyshev distance):p = ∞ p=\infty p = ∞ dist c h ( x i , x j ) = ∥ x i − x j ∥ ∞ = max 1 ⩽ u ⩽ n ∣ x i u − x j u ∣ \operatorname{dist}_{\mathrm{ch}}(\bm{x}_i, \bm{x}_j) = \left\lVert \bm{x}_i - \bm{x}_{j} \right\rVert_\infty = \max_{1 \le u \le n} |x_{iu} - x_{ju}|
dist ch ( x i , x j ) = ∥ x i − x j ∥ ∞ = 1 ⩽ u ⩽ n max ∣ x i u − x j u ∣
属性介绍:
连续属性(continuous attribute):在定义域上有无穷多个可能的取值
离散属性(discrete attribute):在定义域上有有限个可能的取值
有序属性(ordinal attribute):在定义域上有序关系
如定义域为 { 1 , 2 , 3 } \left\lbrace 1, 2, 3 \right\rbrace { 1 , 2 , 3 }
无序属性(non-ordinal attribute):在定义域上无序关系
如定义域为 { red , green , blue } \left\lbrace \text{red}, \text{green}, \text{blue} \right\rbrace { red , green , blue }
不能直接在属性值上进行计算
对于无序属性,可使用 VDM(Value Difference Metrix)。
令 m u , a m_{u, a} m u , a u u u a a a m u , a , i m_{u, a, i} m u , a , i i i i u u u a a a k k k u u u a , b a, b a , b
VDM p ( a , b ) = ∑ i = 1 k ∣ m u , a , i m u , a − m u , b , i m u , b ∣ p \operatorname{VDM}_p(a, b) = \sum_{i=1}^k \left| \dfrac{m_{u, a, i}}{m_{u, a}} - \dfrac{m_{u, b, i}}{m_{u, b}} \right|^p
VDM p ( a , b ) = i = 1 ∑ k m u , a m u , a , i − m u , b m u , b , i p
对于混合属性,可将闵可夫斯基距离和 VDM 结合得到 MinkovDM。
假定有 n c n_c n c n − n c n - n_c n − n c
MinkovDM p ( x i , x j ) = ( ∑ u = 1 n c ∣ x i u − x j u ∣ p + ∑ u = n c + 1 n VDM p ( x i u , x j u ) ) 1 p \operatorname{MinkovDM}_p(\bm{x}_i, \bm{x}_{j}) = \left( \sum_{u=1}^{n_c} \left| x_{iu} - x_{ju} \right|^p + \sum_{u=n_c+1}^{n} \operatorname{VDM}_p(x_{iu}, x_{ju}) \right)^{\frac{1}{p}}
MinkovDM p ( x i , x j ) = ( u = 1 ∑ n c ∣ x i u − x j u ∣ p + u = n c + 1 ∑ n VDM p ( x i u , x j u ) ) p 1
当样本空间中不同属性的重要性不同时,也可以使用「加权距离」(weighted distance),例如加权闵可夫斯基距离
dist w m k ( x i , x j ) = ( ∑ u = 1 n w u ∣ x i u − x j u ∣ p ) 1 p \operatorname{dist}_{\mathrm{wmk}}(\bm{x}_i, \bm{x}_j) = \left( \sum_{u=1}^n w_u |x_{iu} - x_{ju}|^p \right)^{\frac{1}{p}}
dist wmk ( x i , x j ) = ( u = 1 ∑ n w u ∣ x i u − x j u ∣ p ) p 1
其中 w u ⩾ 0 w_u \ge 0 w u ⩾ 0 u u u ∑ u = 1 n w u = 1 \displaystyle \sum_{u=1}^n w_u = 1 u = 1 ∑ n w u = 1
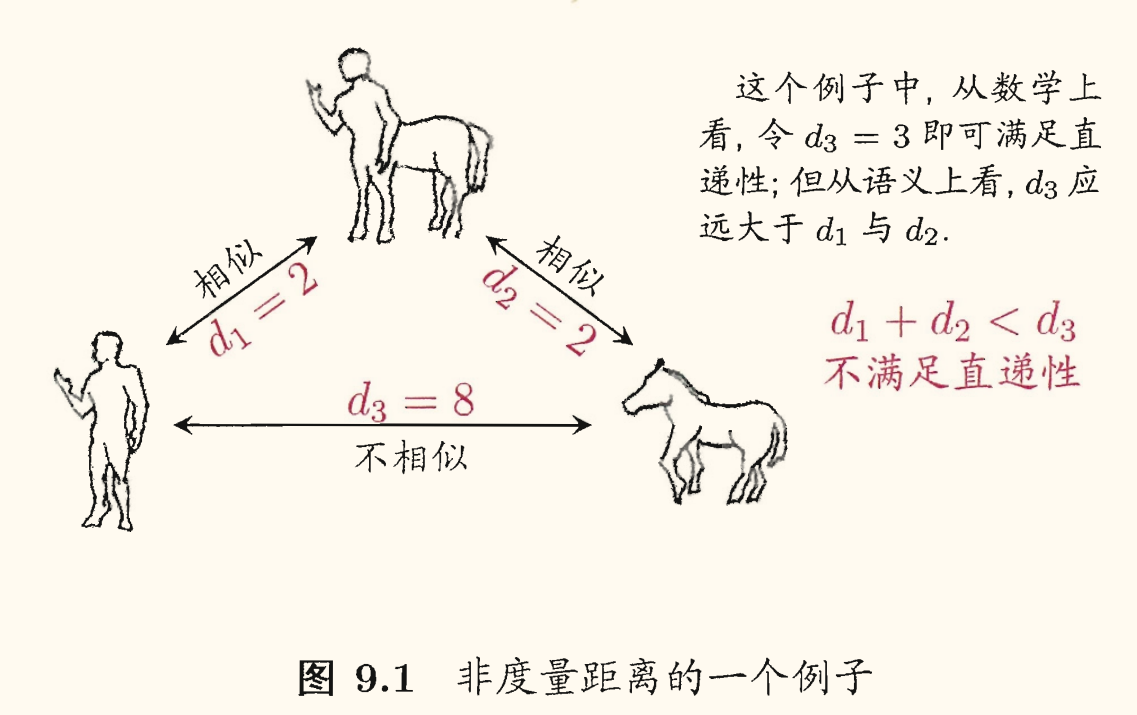
通常我们是基于某种形式的距离来定义「相似度度量」(similarity measure),距离越大,相似度越小。然而用于相似度度量的距离未必满足距离度量的所有基本性质(尤其是直递性)。这样的距离称为「非度量距离」(non-metric distance)。
聚类的「好坏」不存在绝对标准。
老师拿来苹果和梨,让小朋友分成两份。
常见的聚类方法:
原型聚类 ,亦称为「基于原型的聚类」(prototype-based clustering)
假设:聚类结构能通过一组原型刻画
过程:先对原型初始化,然后对原型进行迭代更新求解
代表:k k k 学习向量量化(LVQ) ,高斯混合聚类
密度聚类 ,亦称「基于密度的聚类」(density-based clustering)
假设:聚类结构能通过样本分布的紧密程度确定
过程:从样本密度的角度来考察样本之间的可连接性,并基于可连接样本不断扩展聚类簇
代表:DBSCAN , OPTICS, DENCLUE
层次聚类 (hierarchical clustering)
假设:能够产生不同粒度的聚类结果
过程:在不同层次对数据集进行划分,从而形成树形的聚类结构
代表:AGNES (自底向上),DIANA(自顶向下)
原型聚类
k k k 给定样本集 D = { x i } i = 1 m D = \left\lbrace \bm{x}_i \right\rbrace_{i=1}^m D = { x i } i = 1 m k k k k k k C = { C 1 , ⋯ , C k } \mathcal{C} = \left\lbrace C_1, \cdots, C_k \right\rbrace C = { C 1 , ⋯ , C k }
E = ∑ i = 1 k ∑ x ∈ C i ∥ x − μ i ∥ 2 2 E = \sum_{i=1}^{k} \sum_{\bm{x} \in C_i} \left\lVert \bm{x} - \bm{\mu}_i \right\rVert_2^2
E = i = 1 ∑ k x ∈ C i ∑ ∥ x − μ i ∥ 2 2
其中 μ i = 1 ∣ C i ∣ ∑ x ∈ C i x \bm{\mu}_i = \displaystyle \dfrac{1}{|C_i|} \sum_{\bm{x} \in C_i} \bm{x} μ i = ∣ C i ∣ 1 x ∈ C i ∑ x C i C_i C i
E E E E E E
最小化 E E E D D D
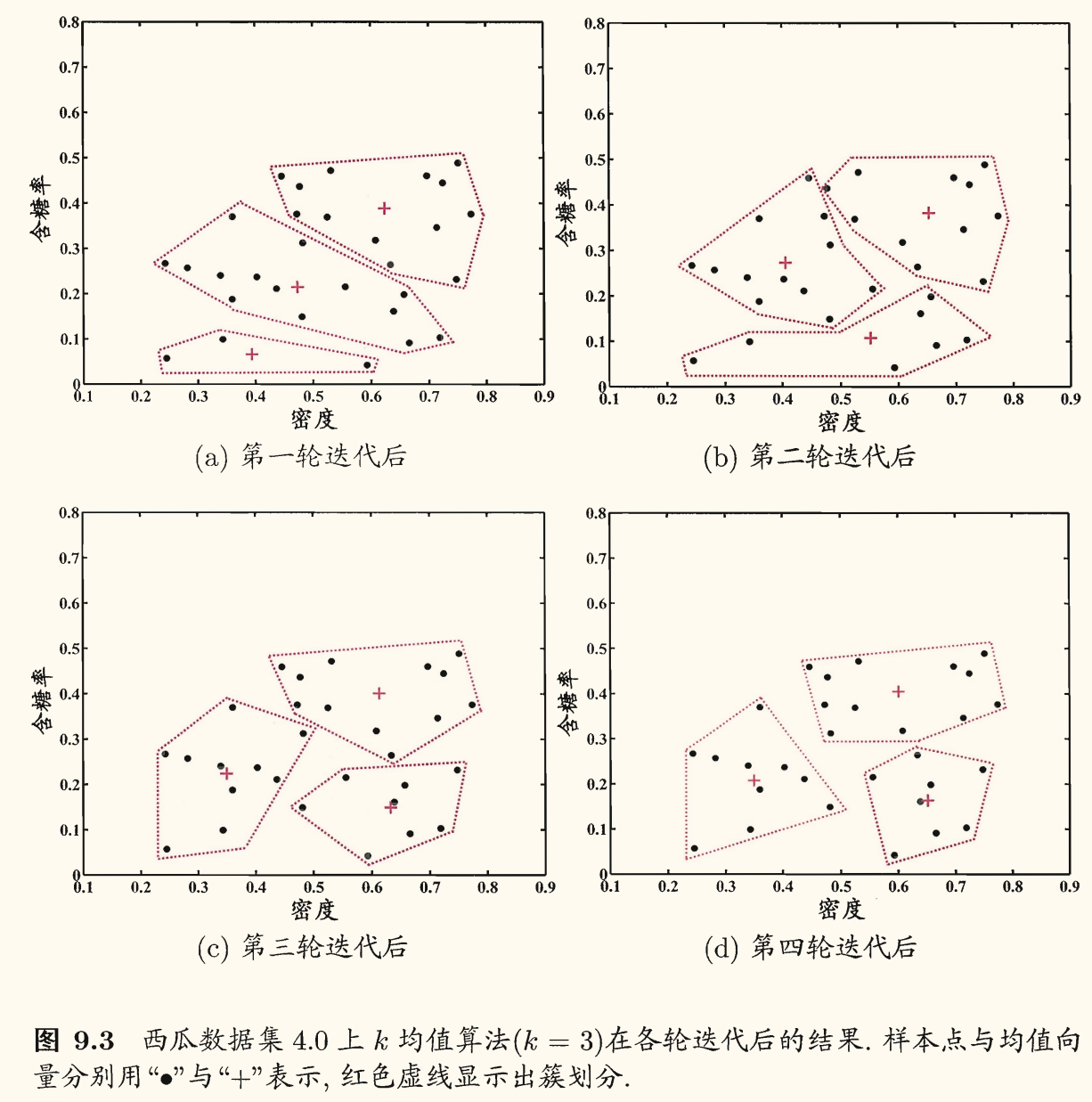
k k k
算法流程:
第 1 行对均值向量进行初始化
第 4 ~ 8 行与第 9 ~ 16 行依次对当前簇划分及均值向量迭代更新
若迭代更新后聚类结果保持不变,则在第 18 行将当前簇划分结果返回
否则继续迭代更新
一些在线模拟网站:
学习向量量化
学习向量量化(Learning Vector Quantization, LVQ)是一种原型聚类算法,与一般聚类算法不同的是,LVQ 假设数据样本带有类别标记,学习过程中利用样本的这些监督信息来辅助聚类。
给定样本集 D = { ( x i , y i ) } i = 1 m D = \left\lbrace (\bm{x}_i, y_i) \right\rbrace_{i=1}^m D = { ( x i , y i ) } i = 1 m x j \bm{x}_{j} x j n n n x j = ( x j 1 ; x j 2 ; ⋯ ; x j n ) \bm{x}_j = (x_{j1}; x_{j2}; \cdots; x_{jn}) x j = ( x j 1 ; x j 2 ; ⋯ ; x j n ) y j ∈ Y y_{j} \in \mathcal{Y} y j ∈ Y x j \bm{x}_{j} x j
LVQ 的目标是学得一组 n n n { p 1 , … , p q } \left\lbrace \bm{p}_1, \dots, \bm{p}_q \right\rbrace { p 1 , … , p q } t i ∈ Y t_i \in \mathcal{Y} t i ∈ Y
LVQ 算法流程如下图所示:
算法流程:
第 1 行先对原型向量进行初始化
例如对第 q q q t q t_q t q
第 2 ~ 12 行对原型向量进行迭代优化:每一轮迭代中,算法随机选取一个有标记的训练样本,找出与其距离最近的原型向量,并根据两者的类别标记是否一致来对原型向量进行相应的更新
第 12 行中,若算法的停止条件已满足(例如已达到最大迭代轮数,或原型向量更新很小甚至不再更新),则将当前原型向量作为最终结果返回
LVQ 的关键在于第 6 ~ 10 行,即如何更新原型向量。
直观上看,对样本 x j \bm{x}_{j} x j p i ∗ \bm{p}_{i^{*}} p i ∗ x j \bm{x}_{j} x j p i ∗ \bm{p}_{i^{*}} p i ∗ x j \bm{x}_{j} x j
p ′ = p i ∗ + η ⋅ ( x j − p i ∗ ) \bm{p}' = \bm{p}_{i^{*}} + \eta \cdot (\bm{x}_{j} - \bm{p}_{i^{*}})
p ′ = p i ∗ + η ⋅ ( x j − p i ∗ )
p ′ \bm{p}' p ′ x j \bm{x}_{j} x j
∥ p ′ − x j ∥ 2 = ∥ p i ∗ + η ⋅ ( x j − p i ∗ ) − x j ∥ 2 = ( 1 − η ) ⋅ ∥ p i ∗ − x j ∥ 2 \begin{aligned}
\left\lVert \bm{p}' - \bm{x}_{j} \right\rVert_2 &= \left\lVert \bm{p}_{i^{*}} + \eta \cdot (\bm{x}_{j} - \bm{p}_{i^{*}}) - \bm{x}_{j} \right\rVert_2\\
&= (1 - \eta) \cdot \left\lVert \bm{p}_{i^{*}} - \bm{x}_{j} \right\rVert_2
\end{aligned}
∥ p ′ − x j ∥ 2 = ∥ p i ∗ + η ⋅ ( x j − p i ∗ ) − x j ∥ 2 = ( 1 − η ) ⋅ ∥ p i ∗ − x j ∥ 2
令学习率 η ∈ ( 0 , 1 ) \eta \in (0, 1) η ∈ ( 0 , 1 ) p i ∗ \bm{p}_{i^{*}} p i ∗ p ′ \bm{p}' p ′ x j \bm{x}_{j} x j
类似地,若最近的原型向量 p i ∗ \bm{p}_{i^{*}} p i ∗ x j \bm{x}_{j} x j x j \bm{x}_{j} x j ( 1 + η ) ⋅ ∥ p i ∗ − x j ∥ 2 (1 + \eta) \cdot \left\lVert \bm{p}_{i^{*}} - \bm{x}_{j} \right\rVert_2 ( 1 + η ) ⋅ ∥ p i ∗ − x j ∥ 2 x j \bm{x}_{j} x j
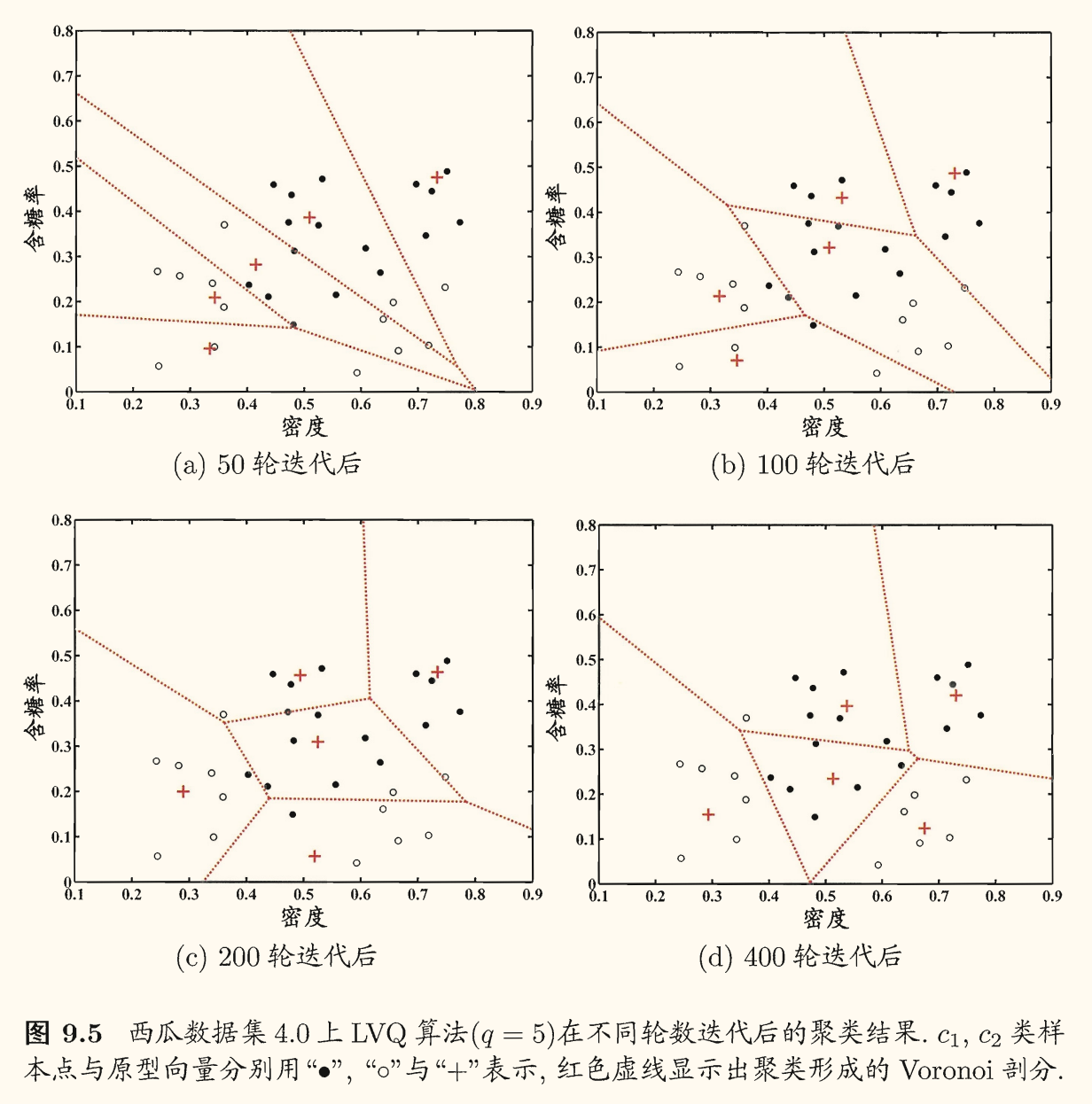
在学得一组原型向量 { p 1 , … , p q } \left\lbrace \bm{p}_1, \dots, \bm{p}_q \right\rbrace { p 1 , … , p q } X \mathcal{X} X
对任意样本 x \bm{x} x p i \bm{p}_i p i R i R_i R i p i \bm{p}_i p i p i ′ \bm{p}_{i'} p i ′
R i = { x ∈ X ∣ ∥ x − p i ∥ 2 ⩽ ∥ x − p i ′ ∥ 2 , i ′ ≠ i } R_i = \left\lbrace \bm{x} \in \mathcal{X} \mid \left\lVert \bm{x} - \bm{p}_i \right\rVert_2 \le \left\lVert \bm{x} - \bm{p}_{i'} \right\rVert_2, i' \ne i \right\rbrace
R i = { x ∈ X ∣ ∥ x − p i ∥ 2 ⩽ ∥ x − p i ′ ∥ 2 , i ′ = i }
从而形成了对样本空间 X \mathcal{X} X { R 1 , … , R q } \left\lbrace R_1, \dots, R_q \right\rbrace { R 1 , … , R q }
下面是一个 LVQ 的聚类结果示例:
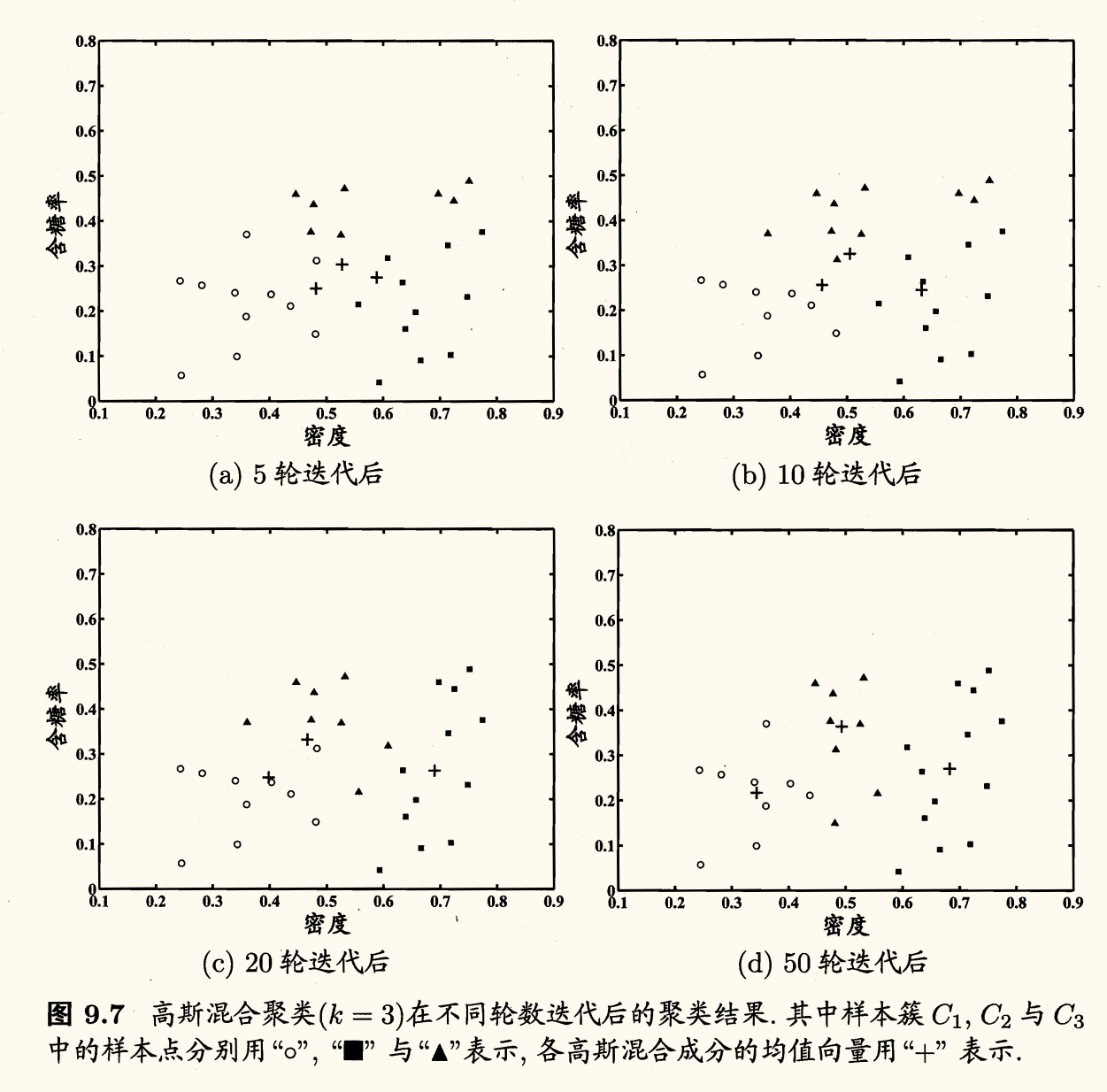
高斯混合聚类
高斯混合聚类(Gaussian Mixture Model, GMM)是一种基于概率模型 的聚类方法,它假设数据是由多个高斯分布混合而成的。
对 n n n X \mathcal{X} X x \bm{x} x x \bm{x} x x ∼ N ( μ , Σ ) \bm{x} \sim \mathcal{N}(\bm{\mu}, \bm{\Sigma}) x ∼ N ( μ , Σ )
p ( x ) = 1 ( 2 π ) n 2 ∣ Σ ∣ 1 2 exp ( − 1 2 ( x − μ ) ⊺ Σ − 1 ( x − μ ) ) p(\bm{x}) = \dfrac{1}{(2\pi)^{\frac{n}{2}} |\bm{\Sigma}|^{\frac{1}{2}}} \exp \left( -\dfrac{1}{2} (\bm{x} - \bm{\mu})^\intercal \bm{\Sigma}^{-1} (\bm{x} - \bm{\mu}) \right)
p ( x ) = ( 2 π ) 2 n ∣ Σ ∣ 2 1 1 exp ( − 2 1 ( x − μ ) ⊺ Σ − 1 ( x − μ ) )
其中 μ \bm{\mu} μ n n n Σ \bm{\Sigma} Σ n × n n \times n n × n
高斯分布完全由均值向量 μ \bm{\mu} μ Σ \bm{\Sigma} Σ p ( x ∣ μ , Σ ) p(\bm{x} \mid \bm{\mu}, \bm{\Sigma}) p ( x ∣ μ , Σ )
可以定义「高斯混合分布」
p M = ∑ i = 1 k α i ⋅ p ( x ∣ μ i , Σ i ) p_{\mathcal{M}} = \sum_{i=1}^{k} \alpha_i \cdot p(\bm{x} \mid \bm{\mu}_i, \bm{\Sigma}_i)
p M = i = 1 ∑ k α i ⋅ p ( x ∣ μ i , Σ i )
该分布由 k k k α i > 0 \alpha_i > 0 α i > 0 ∑ i = 1 k α i = 1 \displaystyle \sum_{i=1}^{k} \alpha_i = 1 i = 1 ∑ k α i = 1
假设样本的生成过程由高斯混合分布给出:首先根据 α 1 , ⋯ , α k \alpha_1, \cdots, \alpha_k α 1 , ⋯ , α k α i \alpha_i α i i i i
若训练集 D = { x i } i = 1 m D = \left\lbrace \bm{x}_i \right\rbrace_{i=1}^m D = { x i } i = 1 m z j ∈ { 1 , ⋯ , k } z_{j} \in \left\lbrace 1, \cdots, k \right\rbrace z j ∈ { 1 , ⋯ , k } x j \bm{x}_{j} x j z j z_{j} z j P ( z j = i ) P(z_{j} = i) P ( z j = i ) α i \alpha_i α i z j z_{j} z j
p M ( z j = i ∣ x j ) = P ( z j = i ) ⋅ p M ( x j ∣ z j = i ) p M ( x j ) = α i ⋅ p ( x j ∣ μ i , Σ i ) ∑ l = 1 k α l ⋅ p ( x j ∣ μ l , Σ l ) \begin{aligned}
p_{\mathcal{M}}(z_{j} = i \mid \bm{x}_{j}) &= \dfrac{P(z_{j} = i) \cdot p_{\mathcal{M}}(\bm{x}_{j} \mid z_{j} = i)}{p_{\mathcal{M}}(\bm{x}_{j})} \\
&= \dfrac{\alpha_i \cdot p(\bm{x}_{j} \mid \bm{\mu}_i, \bm{\Sigma}_i)}{\sum\limits_{l=1}^{k} \alpha_l \cdot p(\bm{x}_{j} \mid \bm{\mu}_l, \bm{\Sigma}_l)}
\end{aligned}
p M ( z j = i ∣ x j ) = p M ( x j ) P ( z j = i ) ⋅ p M ( x j ∣ z j = i ) = l = 1 ∑ k α l ⋅ p ( x j ∣ μ l , Σ l ) α i ⋅ p ( x j ∣ μ i , Σ i )
简记为 γ j i \gamma_{ji} γ j i
换言之,p M ( z j = i ∣ x j ) p_{\mathcal{M}}(z_{j} = i \mid \bm{x}_{j}) p M ( z j = i ∣ x j ) x j \bm{x}_j x j i i i
当高斯混合分布已知时,高斯混合聚类将把样本集 D D D k k k x j \bm{x}_{j} x j λ j \lambda_{j} λ j
λ j = arg max i ∈ { 1 , ⋯ , k } γ j i \lambda_{j} = \argmax_{i \in \left\lbrace 1, \cdots, k \right\rbrace} \gamma_{ji}
λ j = i ∈ { 1 , ⋯ , k } arg max γ j i
从原型聚类的角度上看,高斯混合聚类是采用概率模型(高斯分布)对原型进行刻画,簇划分则由原型对应的后验概率确定。
模型参数 { ( α i , μ i , Σ i ) ∣ 1 ⩽ i ⩽ k } \left\lbrace (\alpha_i, \bm{\mu}_i, \bm{\Sigma}_i) \mid 1 \le i \le k \right\rbrace { ( α i , μ i , Σ i ) ∣ 1 ⩽ i ⩽ k }
L L ( D ) = ln ( ∏ j = 1 m p M ( x j ) ) = ∑ j = 1 m ln ( ∑ i = 1 k α i ⋅ p ( x j ∣ μ i , Σ i ) ) \begin{aligned}
LL(D) &= \ln \left( \prod_{j=1}^{m} p_{\mathcal{M}}(\bm{x}_{j}) \right) \\
&= \sum_{j=1}^{m} \ln \left( \sum_{i=1}^{k} \alpha_i \cdot p(\bm{x}_{j} \mid \bm{\mu}_i, \bm{\Sigma}_i) \right)
\end{aligned}
LL ( D ) = ln ( j = 1 ∏ m p M ( x j ) ) = j = 1 ∑ m ln ( i = 1 ∑ k α i ⋅ p ( x j ∣ μ i , Σ i ) )
常采用 EM 算法进行迭代优化求解:
E 步:根据当前参数计算每个样本属于每个高斯成分的后验概率
M 步:更新模型参数
令 ∂ L L ( D ) ∂ μ i , ∂ L L ( D ) ∂ Σ i = 0 \dfrac{\partial LL(D)}{\partial \bm{\mu}_i}, \dfrac{\partial LL(D)}{\partial \bm{\Sigma}_i} = 0 ∂ μ i ∂ LL ( D ) , ∂ Σ i ∂ LL ( D ) = 0
{ μ i = ∑ j = 1 m γ j i x j ∑ j = 1 m γ j i , Σ i = ∑ j = 1 m γ j i ( x j − μ i ) ( x j − μ i ) ⊺ ∑ j = 1 m γ j i , α i = 1 m ∑ j = 1 m γ j i . \left\lbrace\begin{aligned}
\bm{\mu}_i &= \dfrac{\sum_{j=1}^{m} \gamma_{ji} \bm{x}_{j}}{\sum_{j=1}^{m} \gamma_{ji}},\\
\bm{\Sigma}_i &= \dfrac{\sum_{j=1}^{m} \gamma_{ji} (\bm{x}_{j} - \bm{\mu}_i) (\bm{x}_{j} - \bm{\mu}_i)^\intercal}{\sum_{j=1}^{m} \gamma_{ji}},\\
\alpha_i &= \dfrac{1}{m} \sum_{j=1}^{m} \gamma_{ji}.
\end{aligned}\right.
⎩ ⎨ ⎧ μ i Σ i α i = ∑ j = 1 m γ j i ∑ j = 1 m γ j i x j , = ∑ j = 1 m γ j i ∑ j = 1 m γ j i ( x j − μ i ) ( x j − μ i ) ⊺ , = m 1 j = 1 ∑ m γ j i .
高斯混合聚类算法流程如下图所示:
密度聚类
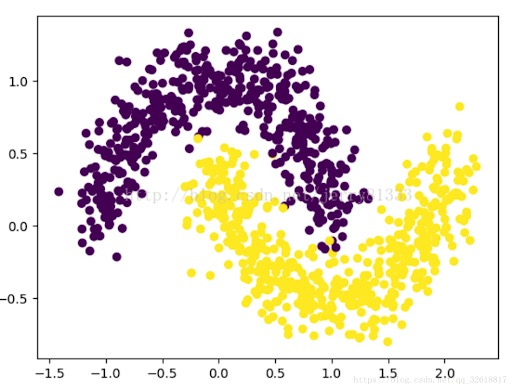
使用 k k k
基于密度的聚类方法:从样本密度的角度考察样本的连接性,使密度相连的样本归结到一个簇,更符合直观认知:
密度聚类 也称为「基于密度的聚类」(density-based clustering)。
此类算法假设聚类结构能通过样本分布的紧密程度 来确定。
通常情况下,密度聚类算法从样本密度的角度来考察样本之间的可连接性,并基于可连接样本不断扩展聚类簇来获得最终的聚类结果。
DBSCAN 算法
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种典型的密度聚类算法,它基于一组「邻域」(neighborhood)参数 ( ϵ , M i n P t s ) (\epsilon, \mathrm{MinPts}) ( ϵ , MinPts )
给定数据集 D = { x i } i = 1 m D = \left\lbrace \bm{x}_i \right\rbrace_{i=1}^m D = { x i } i = 1 m
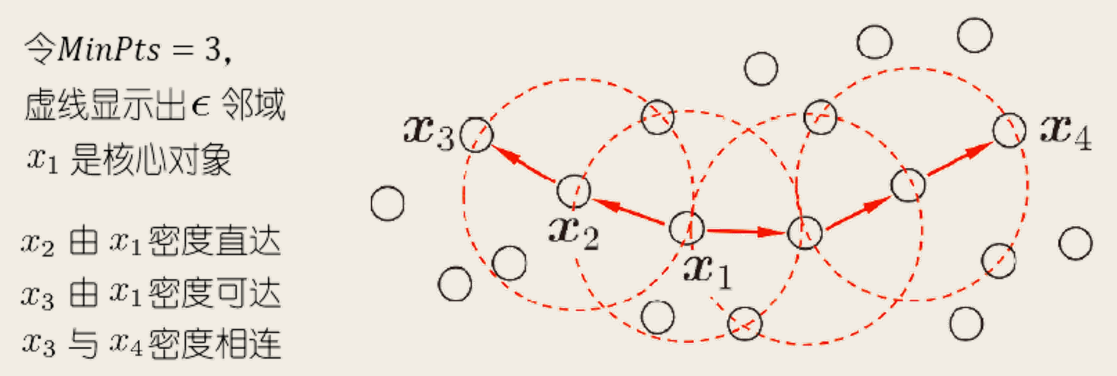
ϵ \epsilon ϵ x j ∈ D \bm{x}_{j} \in D x j ∈ D ϵ \epsilon ϵ D D D x j \bm{x}_{j} x j ϵ \epsilon ϵ N ϵ ( x j ) = { x i ∈ D ∣ dist ( x i , x j ) ⩽ ϵ } N_{\epsilon}(\bm{x}_{j}) = \left\lbrace \bm{x}_i \in D \mid \operatorname{dist}(\bm{x}_i, \bm{x}_{j}) \le \epsilon \right\rbrace N ϵ ( x j ) = { x i ∈ D ∣ dist ( x i , x j ) ⩽ ϵ } 核心对象 (core object):若 x j \bm{x}_{j} x j ϵ \epsilon ϵ M i n P t s \mathrm{MinPts} MinPts ∣ N ϵ ( x j ) ∣ ⩾ M i n P t s |N_{\epsilon}(\bm{x}_{j})| \ge \mathrm{MinPts} ∣ N ϵ ( x j ) ∣ ⩾ MinPts x j \bm{x}_{j} x j 密度直达 (density-reachable):若 x j \bm{x}_{j} x j x i \bm{x}_{i} x i ϵ \epsilon ϵ x i \bm{x}_{i} x i x j \bm{x}_{j} x j x i \bm{x}_{i} x i 密度可达 (density-reachable):对 x i \bm{x}_{i} x i x j \bm{x}_{j} x j { p 1 , ⋯ , p n } \left\lbrace \bm{p}_1, \cdots, \bm{p}_n \right\rbrace { p 1 , ⋯ , p n } p 1 = x i , p n = x j \bm{p}_1 = \bm{x}_{i}, \bm{p}_n = \bm{x}_{j} p 1 = x i , p n = x j p u + 1 \bm{p}_{u+1} p u + 1 p u \bm{p}_u p u x j \bm{x}_{j} x j x i \bm{x}_{i} x i 密度相连 (density-connected):对 x i \bm{x}_{i} x i x j \bm{x}_{j} x j x k \bm{x}_{k} x k x i \bm{x}_{i} x i x j \bm{x}_{j} x j x k \bm{x}_{k} x k x i \bm{x}_{i} x i x j \bm{x}_{j} x j
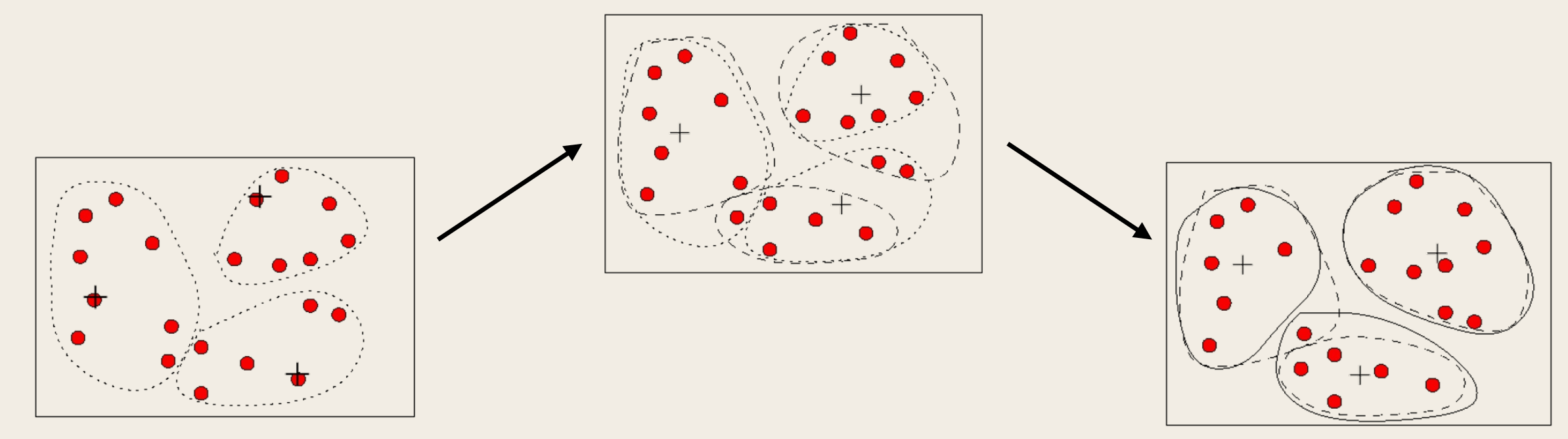
直观显示:
DBSCAN 将「簇」定义为:由密度可达关系导出的最大的密度相连样本集合。
形式化地说,给定邻域参数 ( ϵ , M i n P t s ) (\epsilon, \mathrm{MinPts}) ( ϵ , MinPts ) C ⊆ D C \subseteq D C ⊆ D
连接性(connectivity):x i , x j ∈ C \bm{x}_i, \bm{x}_{j} \in C x i , x j ∈ C x i \bm{x}_i x i x j \bm{x}_{j} x j
最大性(maximality):x i ∈ C \bm{x}_i \in C x i ∈ C x j \bm{x}_{j} x j x i \bm{x}_{i} x i x j ∈ C \bm{x}_{j} \in C x j ∈ C
如何找出满足以上性质的聚类簇?实际上,若 x \bm{x} x x \bm{x} x X = { x ′ ∈ D ∣ x ′ 由 x 密度可达 } X = \left\lbrace \bm{x}' \in D \mid \bm{x}' \text{ 由 } \bm{x} \text{ 密度可达} \right\rbrace X = { x ′ ∈ D ∣ x ′ 由 x 密度可达 }
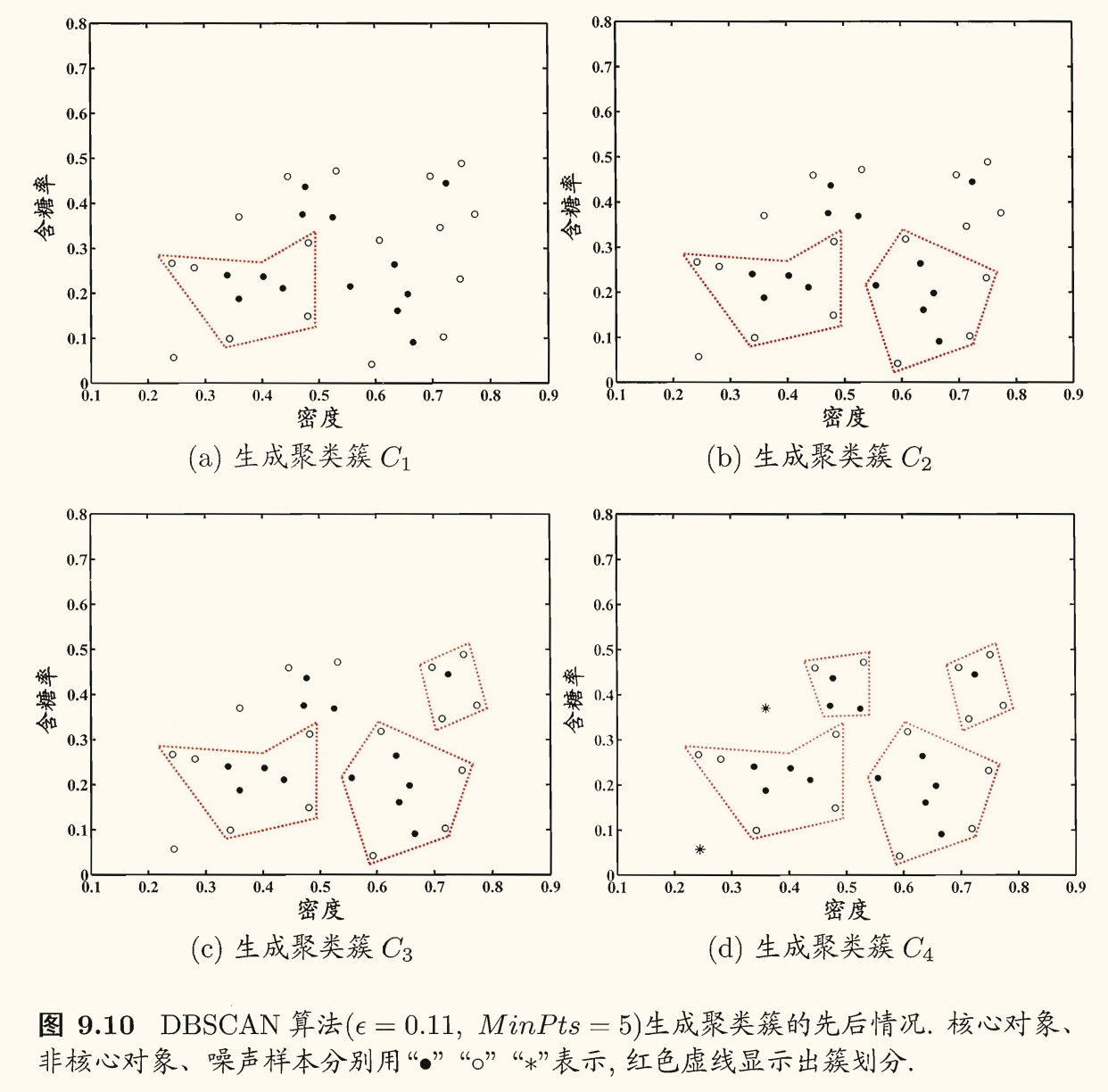
DBSCAN 算法流程如下图所示:
算法流程:
先任选数据集中的一个核心对象为「种子」(seed),再由此出发确定相应的聚类簇
第 1 ~ 7 行中,算法根据给定的邻域参数找出所有核心对象
第 10 ~ 24 行中,以任意核心对象为出发点,找出由其密度可达的样本生成聚类簇,直到所有核心对象均被访问过为止
在线模拟网站:Visualizing DBSCAN Clustering
层次聚类
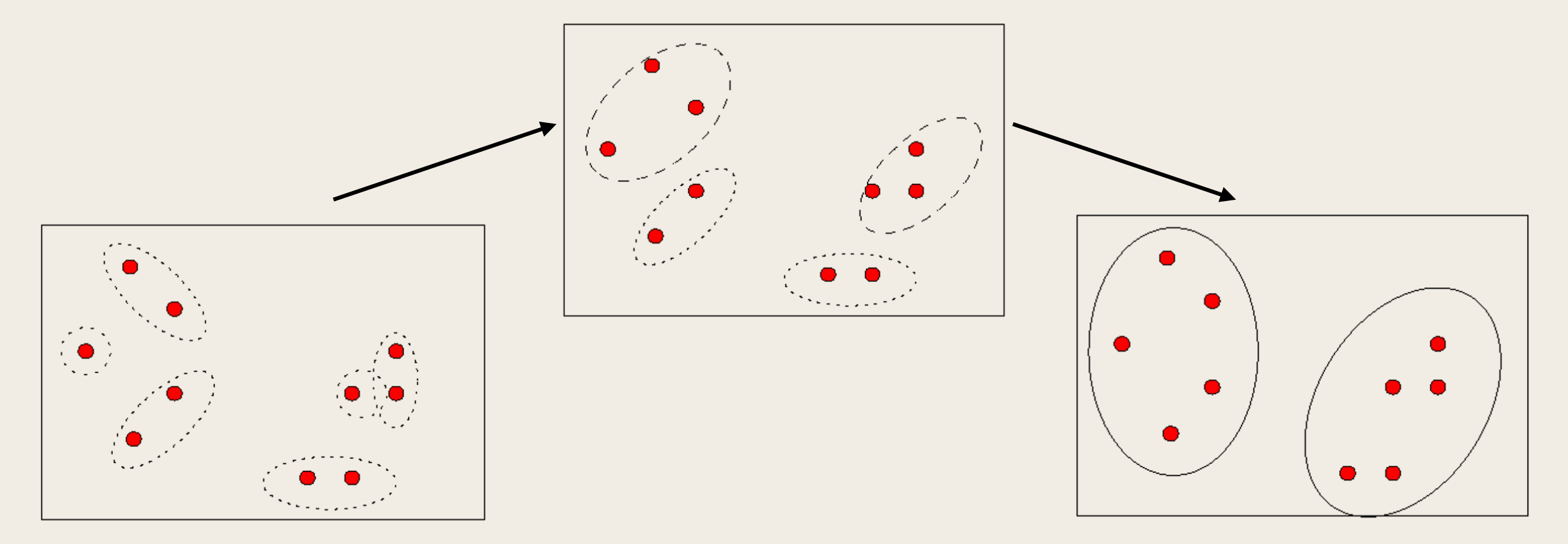
层次聚类 (hierarchical clustering)试图在不同层次对数据集进行划分,从而形成树形的聚类结构。数据集划分既可采用「自底向上」的聚合策略,也可采用「自顶向下」的分拆策略。
AGNES 算法
AGNES (Ag glomerative Nes ting) 是一种采用自底向上聚合策略的层次聚类算法。它先将数据集中的每个样本看作一个初始聚类簇,然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并,该过程不断重复,直至达到预设的聚类簇个数。
这里的关键在于如何计算聚类簇之间的距离。因为每个簇实际上是一个样本集合,因此只需要采用关于集合的某种距离即可。
例如给定聚类簇 C i , C j C_i, C_{j} C i , C j
最小距离 d min ( C i , C j ) = min x i ∈ C i , x j ∈ C j dist ( x i , x j ) d_{\min}(C_i, C_j) = \displaystyle \min_{\bm{x}_i \in C_i, \bm{x}_j \in C_j} \operatorname{dist}(\bm{x}_i, \bm{x}_j) d m i n ( C i , C j ) = x i ∈ C i , x j ∈ C j min dist ( x i , x j )
最大距离 d max ( C i , C j ) = max x i ∈ C i , x j ∈ C j dist ( x i , x j ) d_{\max}(C_i, C_j) = \displaystyle \max_{\bm{x}_i \in C_i, \bm{x}_j \in C_j} \operatorname{dist}(\bm{x}_i, \bm{x}_j) d m a x ( C i , C j ) = x i ∈ C i , x j ∈ C j max dist ( x i , x j )
平均距离 d a v g ( C i , C j ) = 1 ∣ C i ∣ ⋅ ∣ C j ∣ ∑ x i ∈ C i ∑ x j ∈ C j dist ( x i , x j ) \displaystyle d_{\mathrm{avg}}(C_i, C_j) = \dfrac{1}{|C_i| \cdot |C_j|} \sum_{\bm{x}_i \in C_i} \sum_{\bm{x}_j \in C_j} \operatorname{dist}(\bm{x}_i, \bm{x}_j) d avg ( C i , C j ) = ∣ C i ∣ ⋅ ∣ C j ∣ 1 x i ∈ C i ∑ x j ∈ C j ∑ dist ( x i , x j )
当聚类簇距离由以上三种距离之一确定时,AGNES 算法被相应地称为:
单链接 (single-linkage):d ( C i , C j ) = d min ( C i , C j ) d(C_i, C_j) = d_{\min}(C_i, C_j) d ( C i , C j ) = d m i n ( C i , C j ) 全链接 (complete-linkage):d ( C i , C j ) = d max ( C i , C j ) d(C_i, C_j) = d_{\max}(C_i, C_j) d ( C i , C j ) = d m a x ( C i , C j ) 均链接 (average-linkage):d ( C i , C j ) = d a v g ( C i , C j ) d(C_i, C_j) = d_{\mathrm{avg}}(C_i, C_j) d ( C i , C j ) = d avg ( C i , C j )
AGNES 算法流程如下图所示:
算法流程:
第 1 ~ 9 行,算法先对仅含一个样本的初始聚类簇和相应的距离矩阵进行初始化
第 11 ~ 23 行,算法不断合并距离最近的聚类簇,并对合并得到的聚类簇的距离矩阵进行更新
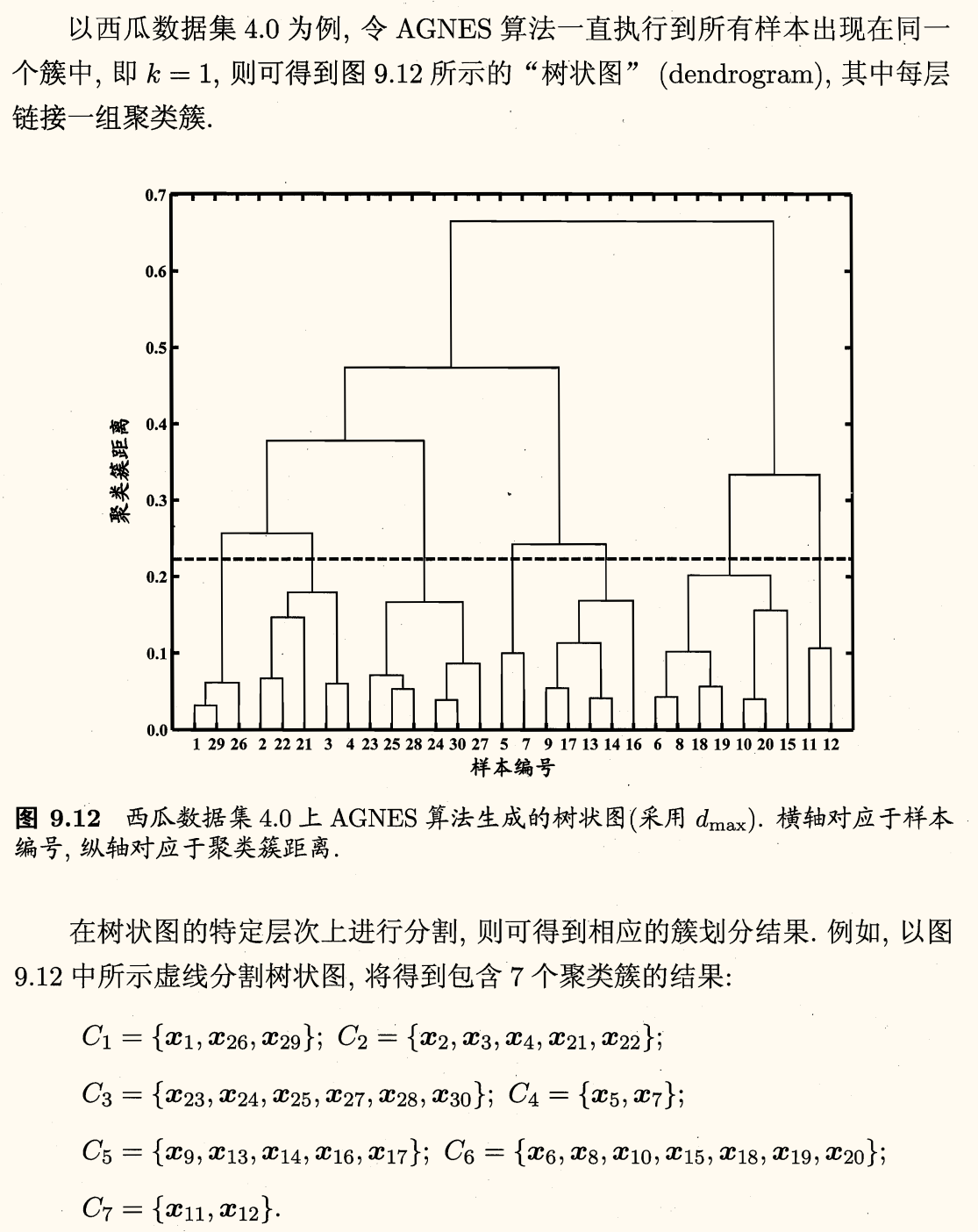
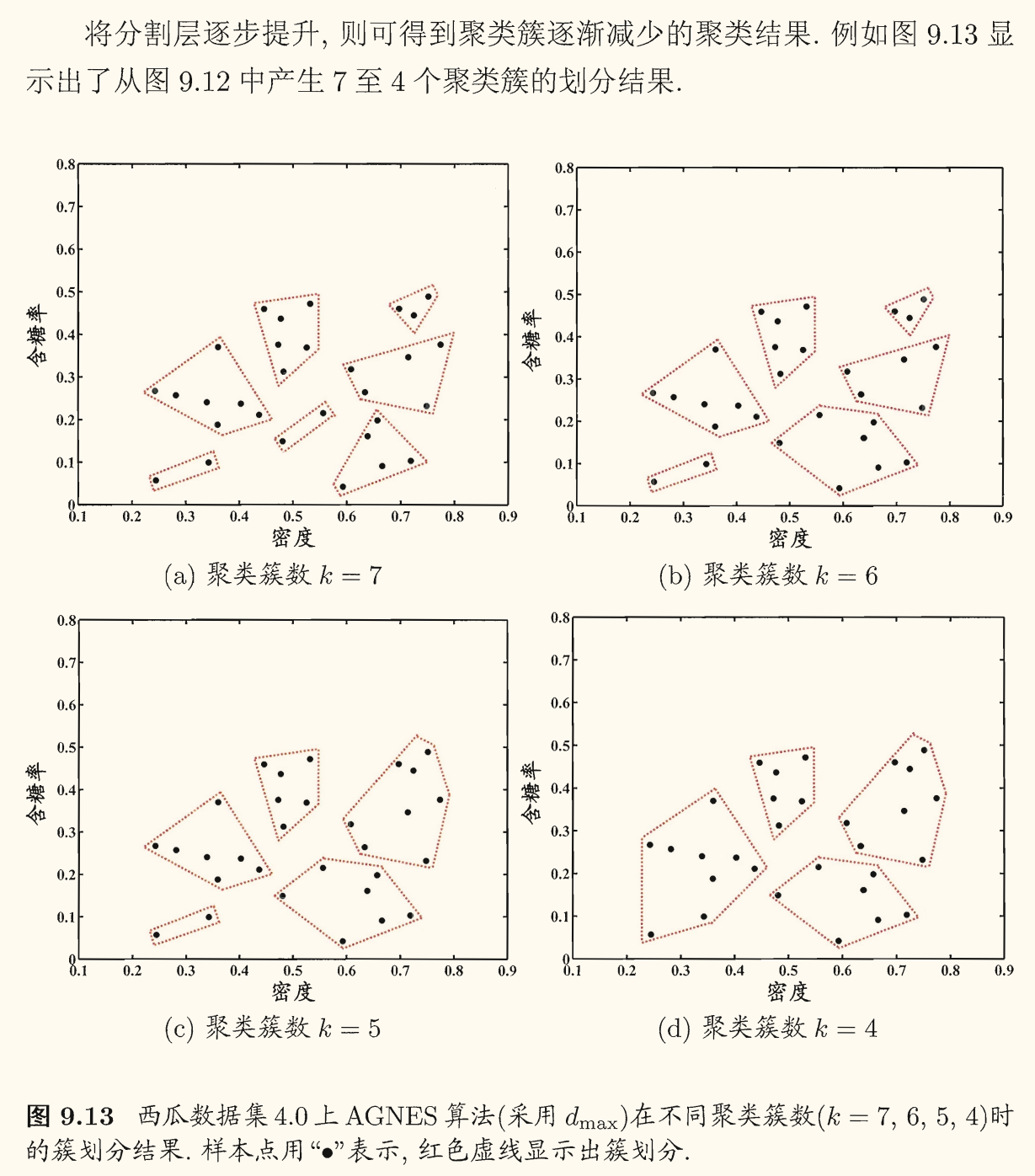
不断重复上述过程,直至达到预设的聚类簇数