特征选择与稀疏学习

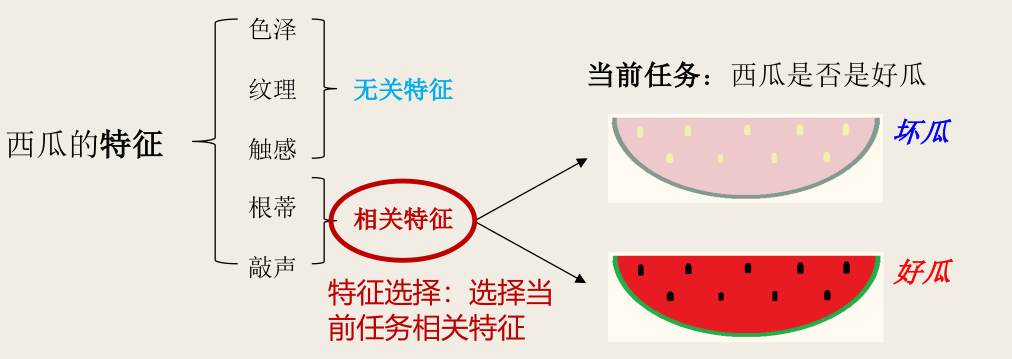
特征（feature）是描述物体的属性。可分类为：

• 相关特征（relevant feature）：对当前的学习任务有用的属性；
• 无关特征（irrelevant feature）：与当前的学习任务无关的属性；
• 冗余特征（redundant feature）：其所包含信息能由其他特征推演出来。

从给定的特征集合中选择出相关特征子集的过程，必须确保不丢失重要特征，称为「特征选择」(feature selection)。

原因：

• 减轻维度灾难：在少量属性上构建模型
• 降低学习难度：留下关键信息

原始的方法有遍历所有可能的子集，但计算上遭遇组合爆炸，实际上不可行。

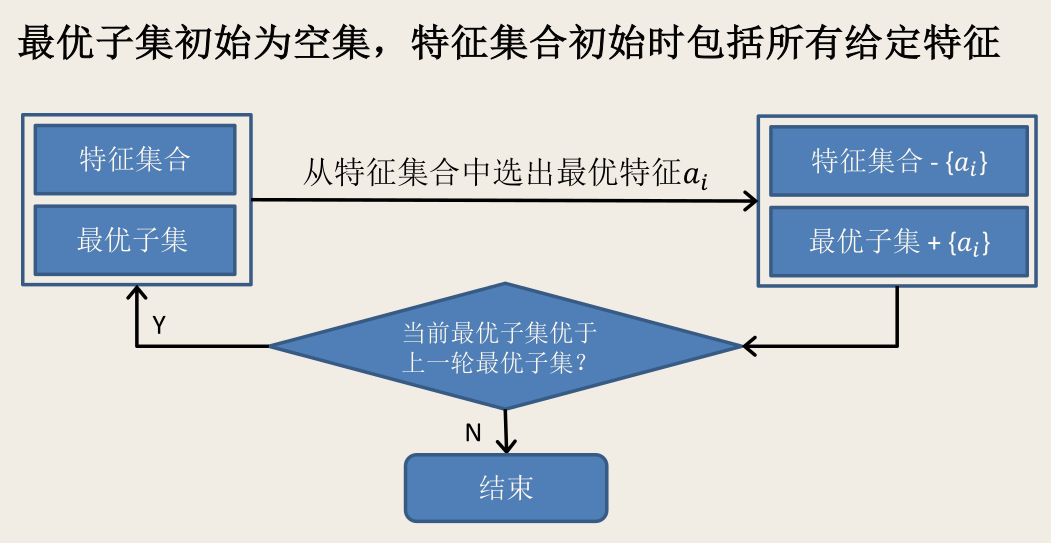
可行方法：

1. 产生初始候选子集；
2. 评价候选子集的好坏；
3. 基于评价结果产生下一个候选子集；
4. 重复步骤 2 和 3，直到满足停止条件。

因此有两个关键环节：子集搜索和子集评价。

子集搜索与评价

子集搜索（subset search）

给定特征集合 $\left\lbrace a_1, \dots, a_d \right\rbrace$，可将每个特征看作一个候选子集。

用贪心策略选择包含重要信息的特征子集：

1. 前向搜索（forward search）：从空集开始，逐渐增加相关特征；
2. 后向搜索（backward search）：从全集开始，逐渐减少无关特征。
3. 双向搜索（bidirectional search）：结合前向和后向搜索，每一轮逐渐增加相关特征，同时逐渐减少无关特征。

前向搜索的流程：

子集评价（subset evaluation）

特征子集确定了对数据集的一个划分，每个划分区域对应着特征子集上的某种取值。如下图所示：

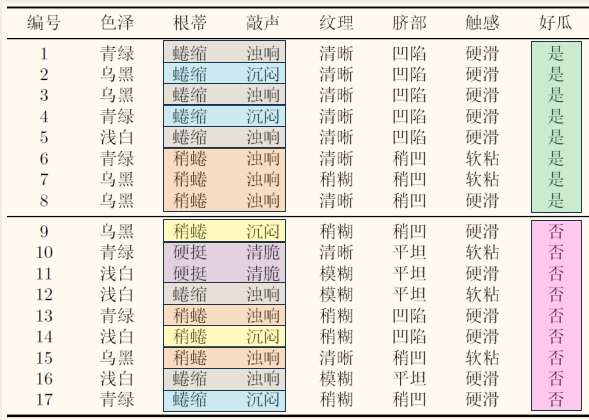
样本标记则对应着对数据集的真实划分。因此通过估算这两个划分的差异，就能对特征子集进行评价，与样本标记对应的划分差异越小，说明当前特征子集越好。

给定数据集 $D$，假定 $D$ 中第 $i$ 类样本所占的比例为 $p_i$，类别数目有 $|\mathcal{Y}|$。

假定样本属性均为离散型，对于属性子集 $A$，假定根据其取值将 $D$ 分成了 $V$ 个子集 $\left\lbrace D^1, \dots, D^V \right\rbrace$，每个子集中的样本在 $A$ 上取值相同。

于是可计算属性子集 $A$ 的信息增益

$$\operatorname{Gain}(A) = \operatorname{Ent}(D) - \sum_{v=1}^V \frac{|D^v|}{|D|} \operatorname{Ent}(D^v)$$

其中信息熵定义为

$$\operatorname{Ent}(D) = - \sum_{i=1}^{|\mathcal{Y}|} p_i \log_2 p_i$$

信息增益 $\operatorname{Gain}(A)$ 越大，意味着特征子集 $A$ 包含的有助于分类的信息越多。

因此对于每个候选特征子集，可基于训练数据集 $D$ 来计算其信息增益，以此作为评价标准。

将特征子集搜索机制与子集评价机制相结合，即可得到特征选择方法。例如将「前向搜索」与「信息熵」相结合，这显然与「决策树」算法非常相似。事实上，决策树可用于特征选择，树结点的划分属性所组成的集合就是选择出的特征子集。

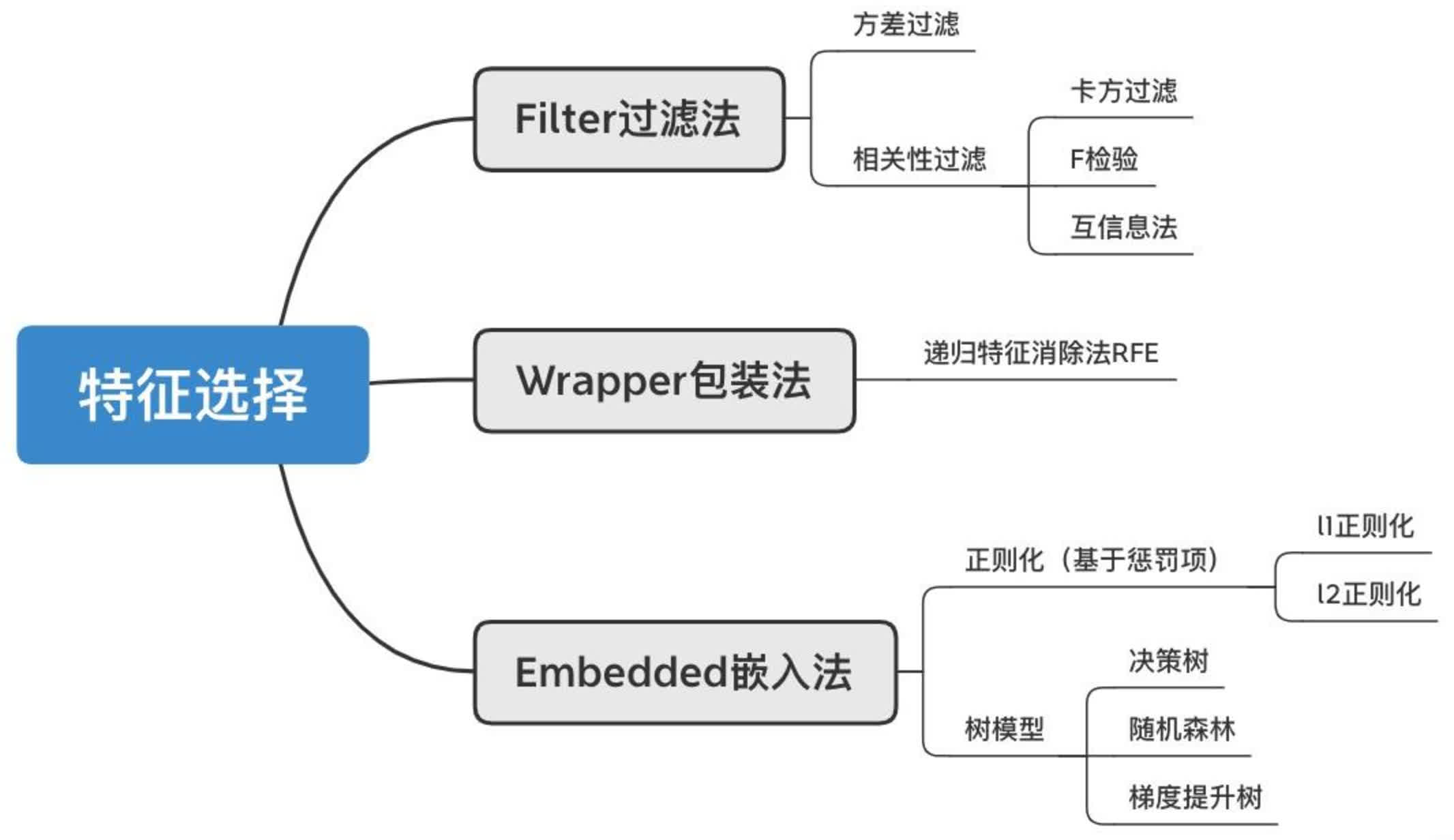
常见的特征选择方法大致可分为三类：

• 过滤式（filter）
• 包裹式（wrapper）
• 嵌入式（embedded）

过滤式选择

「过滤式方法」先对数据集进行特征选择，然后再训练学习器，特征选择过程与后续学习器无关。这相当于先用特征选择过程对初始特征进行「过滤」，再用过滤后的特征来训练模型。

Relief (Relevant Features) 是一种著名的过滤式特征选择方法：

• 为每个初始特征赋予一个「相关统计量」，度量特征的重要性
• 特征子集的重要性由子集中每个特征所对应的相关统计量之和决定
• 设计一个阈值 $\tau$，然后选择比阈值 $\tau$ 大的相关统计量分量所对应的特征
• 或者指定欲选取的特征个数 $k$，然后选择相关统计量分量最大的 $k$ 个特征

因此 Relief 关键是如何确定相关统计量。

给定训练集 $\left\lbrace (\bm{x}_i, y_i) \right\rbrace_{i=1}^m$，对每个示例 $\bm{x}_i$，Relief 定义：

• 猜中近邻（near-hit）：$\bm{x}_i$ 的同类样本中的最近邻 $\bm{x}_{i, \text{nh}}$；
• 猜错近邻（near-miss）：$\bm{x}_i$ 的异类样本中的最近邻 $\bm{x}_{i, \text{nm}}$。

Relief 的相关统计量对应于属性 $j$ 的分量为

$$\delta^{j} = \sum_i - \operatorname{diff}(x_i^{j}, x_{i, \text{nh}}^{j})^2 + \operatorname{diff}(x_i^{j}, x_{i, \text{nm}}^{j})^2$$

其中 $x_a^{j}$ 表示样本 $\bm{x}_a$ 在属性 $j$ 上的取值，$\operatorname{diff}(x_a^{j}, x_b^{j})$ 取决于属性 $j$ 的类型：

• 若 $j$ 为离散型，则 $\operatorname{diff}(x_a^{j}, x_b^{j}) = 1$ 当 $x_a^{j} \ne x_b^{j}$，否则为 $0$；
• 若 $j$ 为连续型，则 $\operatorname{diff}(x_a^{j}, x_b^{j}) = |x_a^{j} - x_b^{j}|$，其中 $x_a^{j}, x_b^{j}$ 已规范化到 $[0, 1]$ 区间。

相关统计量越大，属性 $j$ 上，猜中近邻比猜错近邻越近，即属性 $j$ 对区分对错越有用。

由此可见，Relief 方法是为二分类问题设计的。其扩展变体 Relief-F 能处理多分类问题。

数据集中的样本来自 $|\mathcal{Y}|$ 各类别，其中 $\bm{x}_i$ 属于第 $k$ 类，定义：

• 猜中近邻：第 $k$ 类中 $\bm{x}_i$ 的最近邻 $\bm{x}_{i, \text{nh}}$；
• 猜错近邻：第 $k$ 类之外的每个类中找到一个 $\bm{x}_i$ 的最近邻作为猜错近邻，记为 $\bm{x}_{i, l, \text{nm}}$。

相关统计量对应于属性的份量为

$$\delta^{j} = \sum_i - \operatorname{diff}(x_i^{j}, x_{i, \text{nh}}^{j})^2 + \sum_{l \ne k} \left(p_l \times \operatorname{diff}(x_i^{j}, x_{i, l, \text{nm}}^{j})^2\right)$$

其中 $p_l$ 表示第 $l$ 类样本在数据集 $D$ 中的比例。

包裹式选择

过滤式特征选择不考虑后续学习器，而「包裹式选择」直接把最终将要使用的学习器的性能作为特征子集的评价准则。

包裹式特征选择的目的就是为给定学习器选择最有利于其性能、「量身定做」的特征子集。

包裹式选择方法直接针对给定学习器进行优化，因此从最终学习器性能来看，包裹式特征选择比过滤式特征选择更好。

但另一方面，包裹式特征选择过程中需多次训练学习器，计算开销通常比过滤式特征选择大得多。

LVW (Las Vegas Wrapper) 是一个典型的包裹式特征选择方法。它在「拉斯维加斯方法」（Las Vegas method）^[1]框架下使用随机策略来进行子集搜索，并以最终分类器的误差作为特征子集评价准则。

算法描述如下：

基本步骤：

1. 在循环的每一轮随机产生一个特征子集
2. 在随机产生的特征子集上通过交叉验证推断当前特征子集的误差
3. 进行多次循环，在多个随机产生的特征子集中选择误差最小的特征子集作为最终解

若有运行时间限制，则该算法可能给不出解。

嵌入式选择

「嵌入式特征选择」是将特征选择过程与学习器训练过程融为一体，两者在同一个优化过程中完成，在学习器训练过程中自动地进行特征选择。

考虑线性回归模型，以平方误差为损失函数，引入 $\mathrm{L}_2$ 范数正则化防止过拟合，有

$$\min_{\bm{w}} \sum_{i=1}^{m} \left( y_i - \bm{w}^\intercal \bm{x}_i \right)^2 + \lambda \left\| \bm{w} \right\|_2^2$$

其中正则化参数 $\lambda > 0$。该式称为「岭回归」（ridge regression）。

可以将正则化项中的 $\mathrm{L}_2$ 范数替换为 $\mathrm{L}_1$ 范数，有

$$\begin{equation} \min_{\bm{w}} \sum_{i=1}^{m} \left( y_i - \bm{w}^\intercal \bm{x}_i \right)^2 + \lambda \left\| \bm{w} \right\|_1 \label{1} \end{equation}$$

该式称为 LASSO (Least Absolute Shrinkage and Selection Operator, 最小绝对收缩选择算子)。

$\mathrm{L}_1$ 范数和 $\mathrm{L}_2$ 范数正则化都有助于降低过拟合风险，但前者还会带来一个额外的好处：$\mathrm{L}_1$ 更容易获得「稀疏」（sparse）解，即求得的 $\bm{w}$ 会有更少的非零分量。

直观理解

假设 $\bm{x}$ 仅有两个属性，则 $\bm{w}$ 有两个分量 $w_1, w_2$。

目标优化的解要在平方误差项与正则化项之间折中，即出现在图中平方误差项等值线与正则化等值线相交处：

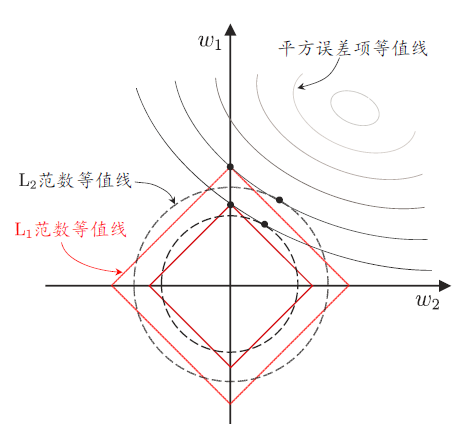
如图所示，采用 $\mathrm{L}_1$ 范数时交点常出现在坐标轴上，即产生 $w_1$ 或 $w_2$ 为零的稀疏解。

好像有点理解了，$\mathrm{L}_1$ 范数是「平」的，而 $\mathrm{L}_2$ 范数「凸」了出来，相较而言更容易在凸出处与平方误差等值线相交，而非在坐标轴上的四个「端点」。

事实上，对 $\bm{w}$ 施加「稀疏约束」，即希望 $\bm{w}$ 的非零分量尽可能少，最自然的是使用 $\mathrm{L}_0$ 范数（非零元素个数），但 $\mathrm{L}_0$ 范数不连续，难以优化求解，因此常使用 $\mathrm{L}_1$ 范数近似。

$\mathrm{L}_1$ 正则化问题的求解可使用「近端梯度下降」（Proximal Gradient Descent, PGD）求解。

$f(\bm{x})$ 二阶泰勒展式为

$$f(\bm{x}) \simeq f(\bm{x}_k) + \left\langle \grad f(\bm{x}_k), \bm{x} - \bm{x}_k \right\rangle + \dfrac{1}{2}(\bm{x} - \bm{x}_{k})^\intercal \dfrac{\delta^2 f(\bm{x}_{k})}{\delta \bm{x}_{k}^2} (\bm{x} - \bm{x}_{k})$$

对优化目标

$$\min_{\bm{x}} f(\bm{x}) + \lambda \left\lVert \bm{x} \right\rVert_1$$

若 $f(\bm{x})$ 可导，且 $\grad f$ 满足 $L$-利普希茨（Lipschitz）条件，即存在常数 $L > 0$ 使得

$$\left\lVert \grad f(\bm{x}') - \grad f(\bm{x}) \right\rVert_2 \le L \left\lVert \bm{x}' - \bm{x} \right\rVert_2$$

对于任意 $\bm{x}, \bm{x}'$ 成立，

将 $L$-利普希茨条件代入泰勒展式，有

$$\begin{aligned} \hat{f}(\bm{x}) &\simeq f(\bm{x}_{k}) + \left\langle \grad f(\bm{x}_k), \bm{x} - \bm{x}_{k} \right\rangle + \dfrac{L}{2} \left\lVert \bm{x} - \bm{x}_{k} \right\rVert_2^2\\ &= f(\bm{x}_{k}) + \grad f(\bm{x}_{k})^\intercal (\bm{x} - \bm{x}_{k}) + \dfrac{L}{2} (\bm{x} - \bm{x}_{k})^\intercal (\bm{x} - \bm{x}_{k})\\ &= \dfrac{L}{2} \left( \left\lVert\bm{x} - \bm{x}_{k}\right\rVert_2^2 + 2 \dfrac{1}{L} \grad f(\bm{x}_{k})^\intercal (\bm{x} - \bm{x}_{k}) + \dfrac{1}{L^2}\left\lVert \grad f(\bm{x}_k) \right\rVert_2^2\right) + f(\bm{x}_k) - \dfrac{1}{2L^2} \left\lVert \grad f(\bm{x}_k) \right\rVert_2^2\\ &= \dfrac{L}{2} \left\lVert \bm{x} - \left(\bm{x}_{k} - \dfrac{1}{L} \grad f(\bm{x}_{k})\right) \right\rVert_2^2 + \text{const} \end{aligned}$$

其中 $\text{const}$ 是与 $\bm{x}$ 无关的常数。因此上式的最小值在

$$\bm{x}_{k+1} = \bm{x}_{k} - \dfrac{1}{L} \grad f(\bm{x}_{k})$$

时取得。

于是通过梯度下降法对 $f(\bm{x})$ 进行最小化，每一步梯度下降迭代实际上等价于最小化二次函数 $\hat{f}(\bm{x})$。

于是可得

$$\bm{x}_{k+1} = \argmin_{\bm{x}} \dfrac{L}{2} \left\lVert \bm{x} - \left(\bm{x}_{k} - \dfrac{1}{L} \grad f(\bm{x}_{k})\right) \right\rVert_2^2 + \lambda \left\lVert \bm{x} \right\rVert_1$$

即在每一步对 $f(\bm{x})$ 进行梯度下降迭代的同时，考虑 $\mathrm{L}_1$ 范数最小化。

对于该式，可先计算 $\bm{z} = \bm{x}_{k} - \dfrac{1}{L} \grad f(\bm{x}_{k})$，然后求解

$$\bm{x}_{k+1} = \argmin_{\bm{x}} \dfrac{L}{2} \left\lVert \bm{x} - \bm{z} \right\rVert_2^2 + \lambda \left\lVert \bm{x} \right\rVert_1$$

令 $x^i$ 表示 $\bm{x}$ 的第 $i$ 个分量，将上式按分量展开可看出，其中不存在 $x^i x^{j}$ 这样的项，即 $\bm{x}$ 的各分量互不影响。

因此上式有闭式解

$$x_{k+1}^i = \begin{cases} z^i - \dfrac{\lambda}{L}, & \dfrac{\lambda}{L} < z^i\\ 0, & |z^i| \le \dfrac{\lambda}{L}\\ z^i + \dfrac{\lambda}{L}, & z^i < -\dfrac{\lambda}{L} \end{cases}$$

其中 $x_{k+1}^i$ 与 $z^i$ 分别是 $\bm{x}_{k+1}$ 与 $\bm{z}$ 的第 $i$ 个分量。

闭式解

按分量展开有

$$\begin{aligned} \dfrac{L}{2}(x^i - z^i)^2 + \lambda |x^i| &= \dfrac{L}{2}x^{i2} - L x^i z^i + \dfrac{L}{2}z^{i2} + \lambda |x^i|\\ &= \begin{cases} \dfrac{L}{2}x^{i2} - (L z^i - \lambda) x^i + \dfrac{L}{2}z^{i2}, & x^i \ge 0\\ \dfrac{L}{2}x^{i2} -(L z^i + \lambda) x^i + \dfrac{L}{2}z^{i2}, & x^i < 0 \end{cases} \end{aligned}$$

是两个二次函数的杂交物，$x^i > 0$ 与 $x^i < 0$ 时对称轴分别为 $z^i - \dfrac{\lambda}{L}$ 与 $z^i + \dfrac{\lambda}{L}$。

当 $z^i > \dfrac{\lambda}{L}$ 时，$x^i < 0$ 时函数恒单调递减，同时在 $x^i > 0$ 时先单调递减，再单调递增，因此最小值在正半边二次函数的对称轴 $z^i - \dfrac{\lambda}{L}$ 处取得，这是第一种情况。

同理，当 $z^i < -\dfrac{\lambda}{L}$ 时，$x^i > 0$ 时函数恒单调递增，同时在 $x^i < 0$ 时先单调递减，再单调递增，因此最小值在负半边二次函数的对称轴 $z^i + \dfrac{\lambda}{L}$ 处取得，这是第三种情况。

而 $|z^i| \le \dfrac{\lambda}{L}$ 时，这时候二者的对称轴都在另一侧，因此负半边始终单调递减，正半边始终单调递增，因此最小值在 $x^i = 0$ 处取得，这是第二种情况。

因此通过 PGD 能使 LASSO 和其他基于 $\mathrm{L}_1$ 范数最小化的方法得以快速求解。

稀疏表示与字典学习

将数据集看成一个矩阵，每行对应一个样本，每列对应一个特征。

特征选择所考虑的问题是特征具有稀疏性，即矩阵中的许多列与当前学习任务无关，可通过特征选择去除这些列，则学习器训练过程仅需在较小的矩阵上进行，学习任务的难度可能有所降低，涉及的计算和存储开销会减小，学得模型的可解释性也会提高。

另一种稀疏性：矩阵中有很多零元素，且非整行整列出现的。

例如文档分类任务中，每个文档看作一个样本，每个字作为一个特征，出现频率或次数作为特征的取值。

稀疏表示的优势：

• 文本数据线性可分
• 存储高效

因此若给定数据集是稠密的，即普通非稀疏数据，能否将其转化为「稀疏表示」（sparse representation）形式呢？

此外我们所希望的稀疏是「恰当稀疏」而非「过度稀疏」。以汉语文档为例，基于《现代汉语常用字表》得到的可能是恰当稀疏，但基于《康熙字典》可能是过度稀疏。

为普通稠密表达的样本找到合适的字典，将样本转化为稀疏表示，这一过程称为「字典学习」（dictionary learning）或「码书学习」（codebook learning）或「稀疏编码」（sparse coding）。

给定数据集 $\left\lbrace \bm{x}_i \right\rbrace_{i=1}^m$，学习目标是字典矩阵 $\mathbf{B} \in \R^{d \times k}$，以及样本 $\bm{x}_i \in \R^d$ 的稀疏表示 $\bm{\alpha}_i \in \R^{k}$，其中 $d$ 是样本维度，$k$ 称为字典的词汇量（通常由用户指定）。

最简单的字典学习的优化形式为

$$\begin{equation} \min_{\mathbf{B}, \bm{\alpha}_i} \sum_{i=1}^m \left\lVert \bm{x}_i - \mathbf{B} \bm{\alpha}_i \right\rVert_2^2 + \lambda \left\lVert \bm{\alpha}_i \right\rVert_1 \label{2} \end{equation}$$

第一项希望由 $\bm{\alpha}_i$ 能很好地重构 $\bm{x}_i$，第二项希望 $\bm{\alpha}_i$ 尽量稀疏。

与 LASSO $\eqref{1}$ 相比，除了类似 $\bm{w}$ 的 $\bm{\alpha}_i$ 外，还需学习字典矩阵 $\mathbf{B}$。

可采用「变量交替优化」的策略求解 $\eqref{2}$。

1. 固定字典 $\mathbf{B}$，按分量展开 $\eqref{2}$，其中不含 $\alpha_i^u \alpha_i^v$ 的交叉项，可参照 LASSO 解法求解下式，从而为每个样本 $\bm{x}_i$ 找到相应的 $\bm{\alpha}_i$

$$\min_{\bm{\alpha}_i} \left\lVert \bm{x}_i - \mathbf{B} \bm{\alpha}_i \right\rVert_2^2 + \lambda \left\lVert \bm{\alpha}_i \right\rVert_1$$

2. 固定 $\bm{\alpha}_i$ 更新字典 $\mathbf{B}$，可改写 $\eqref{2}$ 为

$$\min_{\mathbf{B}} \left\lVert \mathbf{X} - \mathbf{B} \mathbf{A} \right\rVert_F^2$$

其中 $\mathbf{X} = (\bm{x}_1, \dots, \bm{x}_m) \in \R^{d \times m},\, \mathbf{A} = (\bm{\alpha}_1, \dots, \bm{\alpha}_m) \in \R^{k \times m}$，$\left\lVert \cdot \right\rVert_F$ 是矩阵的 Frobenius 范数，即矩阵元素平方和的平方根。

常用基于「逐列更新策略」的 KSVD。

令 $\bm{b}_i$ 表示字典矩阵 $\mathbf{B}$ 的第 $i$ 列，$\bm{\alpha}^i$ 表示稀疏矩阵 $\mathbf{A}$ 的第 $i$ 行，可重写优化目标为

$$\begin{aligned} \min_{\mathbf{B}} \left\lVert \mathbf{X} - \mathbf{B} \mathbf{A} \right\rVert_F^2 &= \min_{\bm{b}_i} \left\lVert \mathbf{X} - \sum_{j=1}^k \bm{b}_j \bm{\alpha}^j \right\rVert_F^2\\ &= \min_{\bm{b}_i} \left\lVert \left(\mathbf{X} - \sum_{j \ne i} \bm{b}_j \bm{\alpha}^j\right) - \bm{b}_i \bm{\alpha}^i \right\rVert_F^2\\ &= \min_{\bm{b}_i} \left\lVert \mathbf{E}_i - \bm{b}_i \bm{\alpha}^i \right\rVert_F^2 \end{aligned}$$

更新字典第 $i$ 列时，其他各列都是固定的，即 $\mathbf{E}_i = \mathbf{X} - \sum_{j \ne i} \bm{b}_j \bm{\alpha}^j$ 是固定的。

于是最小化 $\left\lVert \mathbf{E}_i - \bm{b}_i \bm{\alpha}^i\right\rVert$ 原则上只需对 $\mathbf{E}_i$ 进行奇异值分解，取最大奇异值对应的正交向量。但直接对 $\mathbf{E}_i$ 进行奇异值分解会同时修改 $\bm{b}_i$ 与 $\bm{\alpha}^i$，从而可能破坏 $\mathbf{A}$ 的稀疏性。

因此 KSVD 对 $\mathbf{E}_i$ 与 $\bm{\alpha}^i$ 进行专门处理：

• $\bm{\alpha}^i$ 仅保留非零元素；
• $\mathbf{E}_i$ 仅保留 $\bm{b}_i$ 与 $\bm{\alpha}^i$ 的非零元素的乘积项。

然后再进行奇异值分解，就保持了第一步所得到的稀疏性。

初始化字典矩阵后反复迭代上面两步，最终可求得字典 $\mathbf{B}$ 和样本 $\bm{x}_i$ 的稀疏表示 $\bm{\alpha}_i$。上述字典学习过程中，用户通过设置词汇量 $k$ 来控制字典的规模，从而影响稀疏程度。

压缩感知

在现实任务中，我们常希望根据部分信息来恢复全部信息。

例如为了便于传输、存储，实践中人们通常对采样的数字信号进行压缩，可能损失一些信息。同时信号传输过程中，由于信道出现丢包等问题，又可能损失部分信息。

「压缩感知」（compressed sensing）为解决此类问题提供了新的思路。

长度为 $m$ 的离散信号 $\bm{x}$，用远小于奈奎斯特采样定理^[2]要求的采样率采样得到的长度为 $n$ 的采样后信号 $\bm{y}$，其中 $n \ll m$，即

$$\bm{y} = \bm{\Phi} \bm{x}$$

其中 $\bm{\Phi} \in \R^{n \times m}$ 是对信号 $\bm{x}$ 的测量矩阵，它确定了以什么频率进行采样，以及如何将采样样本组成采样后的信号。

一般情况下 $n \ll m$，不能利用 $\bm{y}$ 还原 $\bm{x}$。因此 $\bm{y}, \bm{x}, \bm{\Phi}$ 组成的上面的方程是一个「欠定方程」（underdetermined system），有无穷多解，无法轻易求出数值解。

但若存在某个线性变换 $\bm{\Psi} \in \R^{m \times m}$ 使得 $\bm{x} = \bm{\Psi} \bm{s}$，其中 $\bm{s}$ 是稀疏向量，即

$$\bm{y} = \bm{\Phi} \bm{x} = \bm{\Phi} \bm{\Psi} \bm{s} = \mathbf{A} \bm{s}$$

其中 $\mathbf{A} = \bm{\Phi} \bm{\Psi} \in \R^{n \times m}$，于是若能根据 $\bm{y}$ 恢复出 $\bm{s}$，则可通过 $\bm{x} = \bm{\Psi} \bm{s}$ 恢复出信号 $\bm{x}$。

若 $\bm{s}$ 具有稀疏性，这个问题可以很好地得到解决。这是因为稀疏性使得未知因素的影响大为减少。此时 $\bm{\Psi}$ 称为「稀疏基」（sparse basis），$\bm{s}$ 称为「稀疏表示」（sparse representation）。

事实上，在很多应用中均可获得具有稀疏性的 $\bm{s}$，例如图像或声音的数字信号通常在时域上不具有稀疏性，但经过傅里叶变换、余弦变换、小波变换等处理后却会转化为频域上的稀疏信号。

限定等距性（Restricted Isometry Property, RIP）

对 $\mathbf{A} \in \R^{n \times m}$，其中 $n \ll m$，若存在常数 $\delta_{k} \in (0, 1)$ 是的对于任意向量 $\bm{s}$ 和 $\mathbf{A}$ 的所有子矩阵 $\mathbf{A}_{k} \in \R^{n \times k}$ 有

$$(1 - \delta_{k}) \left\lVert \bm{s} \right\rVert_2^2 \le \left\lVert \mathbf{A}_{k} \bm{s} \right\rVert_2^2 \le (1 + \delta_{k}) \left\lVert \bm{s} \right\rVert_2^2$$

则称 $\mathbf{A}$ 满足 $k$ 限定等距性（$k$-RIP）。

此时可通过下面的优化问题近乎完美地从 $\bm{y}$ 中恢复出稀疏信号 $\bm{s}$：

$$\min_{\bm{s}} \left\lVert \bm{s} \right\rVert_0\quad \text{s.t.}\quad \bm{y} = \mathbf{A} \bm{s}$$

这涉及 $\mathrm{L}_0$ 范数的最小化，是个 NP 难问题。不过 $\mathrm{L}_1$ 范数最小化一定条件下与 $\mathrm{L}_0$ 范数最小化问题共解，于是只需关注

$$\min_{\bm{s}} \left\lVert \bm{s} \right\rVert_1\quad \text{s.t.}\quad \bm{y} = \mathbf{A} \bm{s}$$

这样压缩感知问题就通过 $\mathrm{L}_1$ 范数最小化问题求解。例如上式可转化为 LASSO 的等价形式，再通过近端梯度下降法求解，即使用「基寻踪去噪」（Basis Pursuit De-Nosising）。

基于部分信息来恢复全部信息的技术在许多现实任务中有重要应用。例如下表，给出了部分客户对书籍的喜好程度评分：

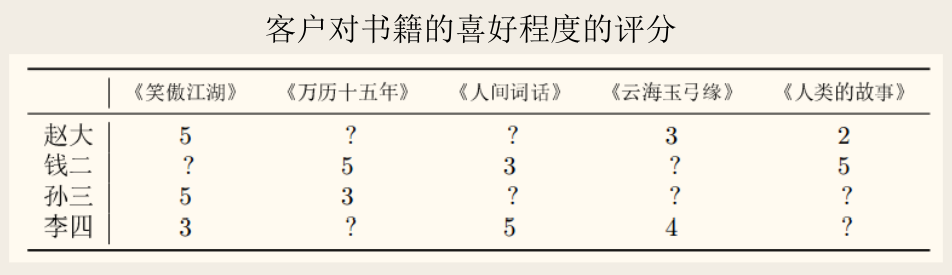
能否将表中已经通过读者评价得到的数据当作「部分信号」，基于压缩感知的思想「恢复」出「完整信号」从而进行书籍推荐呢？从题材、作者、装帧等角度看（相似题材的书籍有相似的读者），表中反映的信号是「稀疏」的，能通过类似压缩感知的思想加以处理。

可以通过「矩阵补全」（matrix completion）技术来处理这类问题。其形式为

$$\min_{\mathbf{X}} \rank(\mathbf{X})\quad \text{s.t.}\quad (\mathbf{X})_{ij} = (\mathbf{A})_{ij},\, (i, j) \in \Omega$$

其中 $\mathbf{X}$ 表示需恢复的稀疏信号，$\mathbf{A}$ 表示已观测信号，$\Omega$ 表示 $\mathbf{A}$ 中已观测到的元素的下标集合。

约束表明，恢复出的矩阵 $\mathbf{X}_{ij}$ 应与已观测的对应元素相同。

这是一个 NP 难问题。注意到 $\rank(\mathbf{X})$ 在集合 $\left\lbrace \mathbf{X} \in \R^{m \times n}\colon \left\lVert \mathbf{X} \right\rVert_F^2 \right\rbrace$ 上的凸包是 $\mathbf{X}$ 的「核范数」（nuclear norm）

$$\left\lVert \mathbf{X} \right\rVert_{*} = \sum_{j=1}^{\min\{m, n\}} \sigma_j(\mathbf{X})$$

其中 $\sigma_{j}(\mathbf{X})$ 表示 $\mathbf{X}$ 的奇异值，即矩阵的核范数为矩阵的奇异值之和。

于是可通过最小化矩阵核范数来近似求解矩阵补全问题：

$$\min_{\mathbf{X}} \left\lVert \mathbf{X} \right\rVert_{*}\quad \text{s.t.}\quad (\mathbf{X})_{ij} = (\mathbf{A})_{ij},\, (i, j) \in \Omega$$

这是一个凸优化问题，可通过「半正定规划」（Semi-Definite Programming, SDP）求解。

理论研究表明，在满足一定条件时，若 $\mathbf{A}$ 秩为 $r$，$n \ll m$，则只需观察到 $O(m r \log^2 m)$ 个元素就能完美恢复出 $\mathbf{A}$。

---

1. 若有时间限制，拉斯维加斯方法或者会返回一个满足要求的解，或者不给出解；蒙特卡罗法一定会给出解，虽然解未必满足要求。若无时间限制，两者都能给出满足要求的解。 ↩︎

2. 奈奎斯特采样定理指出，对于带宽有限的信号，若要完全恢复信号，采样频率至少是信号频率的两倍。 ↩︎