规则学习

基本概念

机器学习中的规则（rule）通常是指语义明确、能描述数据分布所隐含的客观规律或领域概念、可写成「若……，则……」形式的逻辑规则。规则学习（rule learning）是指从训练数据中学习出一组能用于对未见示例进行判别的规则。

例如：

• 回归：若 $\hat{h}(\mathbf{x}) = \hat{y}$，则 $y = \hat{y}$
• 分类：若 $h(\mathbf{x}) > 0$，则判定为正类；否则判定为负类
• 聚类：若 $\forall j \ne i, \operatorname{dist}(\mathbf{x}, c_i) \le \operatorname{dist}(\mathbf{x}, c_{j})$，则 $C(\mathbf{x}) = c_i$

规则学习是机器学习中以符号规则为模型表达方式的一个分支。

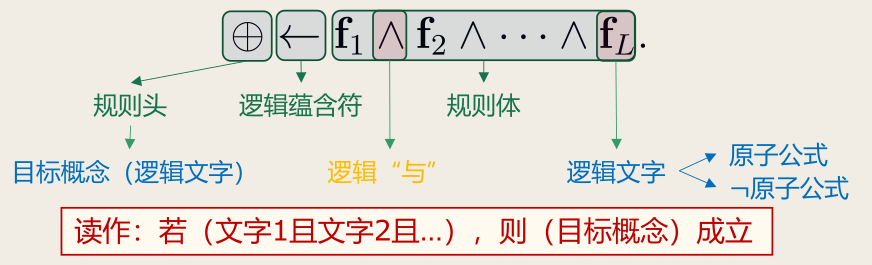
形式化地看，一条规则形如

$$\oplus \gets \mathbf{f}_1 \land \mathbf{f}_2 \land \dots \land \mathbf{f}_L$$

其中

• 逻辑蕴含符号 $\gets$ 右边部分称为「规则体」（body），表示该条规则的前提
  • 由逻辑文字（literal）$\mathbf{f}_{k}$ 组成的合取式
  • 每个文字 $\mathbf{f}_{k}$ 是对示例属性进行检验的布尔表达式
  • $L$ 是规则体中逻辑文字的个数，称为规则的「长度」
• 左边部分称为「规则头」（head），表示该条规则的结果
  • $\oplus$ 也是逻辑文字，一般用于表示规则所判定的目标类别或概念

上面这样的逻辑规则称为「if-then 规则」。

规则学习相较于神经网络、SVM 这样的黑箱模型，具有较好的可解释性，能使用户更直观地对判别过程有所了解。

规则集合中的每条规则都可看作一个子模型，规则集合是这些子模型的一个集成。当同一个示例被判别结果不同的多条规则覆盖时，称发生了冲突（conflict），解决冲突的办法称为「冲突消解」（conflict resolution），常用的冲突消解策略有：

• 投票法：判别相同的规则数最多的结果作为最终结果；
• 排序法：在规则集合上定义一个顺序，在发生冲突时使用排序最前的规则；
  • 相应的规则学习过程称为「带序规则」（ordered rule）学习或「优先级规则」（priority rule）学习。
• 元规则法：根据领域知识事先设定一些「元规则」（meta-rule），即关于规则的规则，根据元规则的指导使用规则集。
  • 如「发生冲突时使用长度最小的规则」就是一个元规则。

从训练集学得的规则集合也许不能覆盖所有可能的未见示例，因此规则学习算法通常会设置一条默认规则（default rule, 缺省规则），用于对未被覆盖的示例进行判别。

规则可分为两类：

• 命题规则（propositional rule）：由「原子命题」（propositional atom）和逻辑连接词（$\land , \lor , \lnot , \gets$）构成的简单陈述句；
• 一阶规则（first-order rule, 关系型规则 relational rule）：基本成分是能描述事物的属性或关系的「原子公式」（atomic formula）。

例如谓词是原子公式，比如说 $P(x)$，$Q(x, y)$，$R(x, y, z)$ 等。$\forall X(\operatorname{自然数}(\sigma(X)) \gets \operatorname{自然数}(X))$ 是一个一阶规则，其中 $X$ 称为「逻辑变量」，$\forall , \exists$ 限定变量的取值范围，称为「量词」（quantifier）。

从形式化语言系统来看，命题规则是一阶规则的特例。

序贯覆盖

规则学习的目标是产生一个能覆盖尽可能多的样例的规则集。最直接的做法是序贯覆盖（sequential covering），即逐条归纳：在训练集上每学到一条规则，就将该规则覆盖的训练样例去除，然后以剩下的训练样例组成训练集重复上述过程。

由于每次只处理一部分数据，因此也被称为「分治」（separate-and-conquer）。

流程如下：

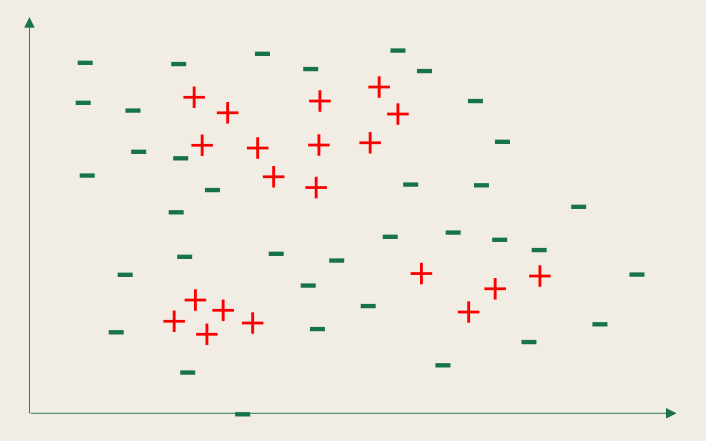
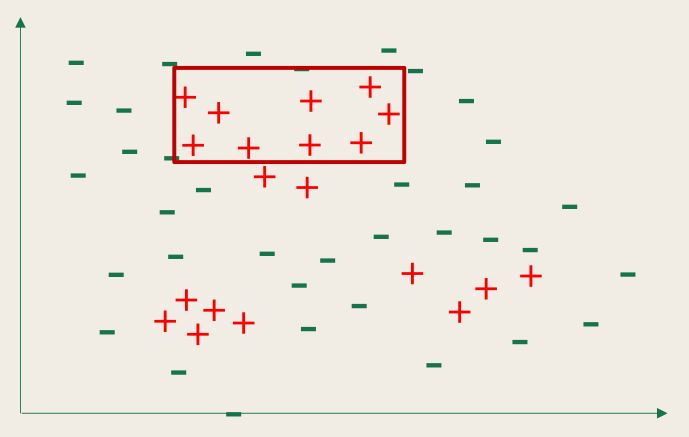
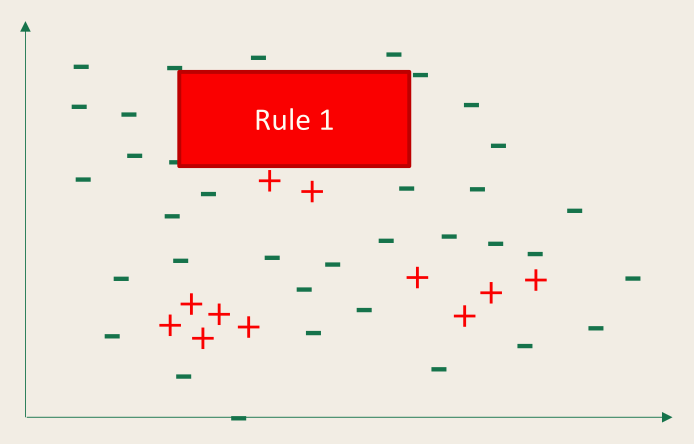
因为非考试范围，所以【待补充】，等寒假有时间补吧。

剪枝优化

一阶规则学习

归纳逻辑程序设计