强化学习
在学习过程中,若将学习目标作为学习过程的「奖赏」,在过程中执行某个操作时,并不能立即获得这个奖赏,甚至难以判断当前操作对最终奖赏的影响,仅能得到一个当前的反馈。需要进行多次学习,在过程中不断摸索,才能总结出好的一套行为规则。这个过程抽象出来就是强化学习(reinforcement learning, 再励学习)。
例如考虑种西瓜,种瓜有许多步骤,经过一段时间才能收获西瓜。通常要等到收获后,我们才知道种出的瓜好不好。若将得到好瓜作为辛勤种瓜劳动的奖赏,则在种瓜过程中当我们执行某个操作(例如,施肥)时,仅能得到一个当前反馈(例如,瓜苗看起来更健壮了)。我们需多次种瓜,在种瓜过程中不断摸索,然后才能总结出较好的种瓜策略。

强化学习常用马尔可夫决策过程(Markov Decision Process, MDP)描述:
- 机器所处的环境 E
- 状态空间 X 是机器感知到的环境的描述
- 智能体能采取的行为空间 A
- 潜在的状态转移函数 P:X×A×X→R
- 瓜苗当前状态缺水,选择动作浇水,有一定概率恢复健康,也有一定概率无法恢复
- 潜在的奖赏(reward)函数 R:X×A×R→R(或 R:X×X→R,即仅与状态转移有关)
- 瓜苗健康对应奖赏 +1,瓜苗凋零对应奖赏 −10,最终种出了好瓜对应奖赏 +100
- 策略(policy):π:X→A(或 π:X×A→R)
综合来看,强化学习任务对应了四元组 E=⟨X,A,P,R⟩。如下图所示是一个马尔可夫决策过程的例子:
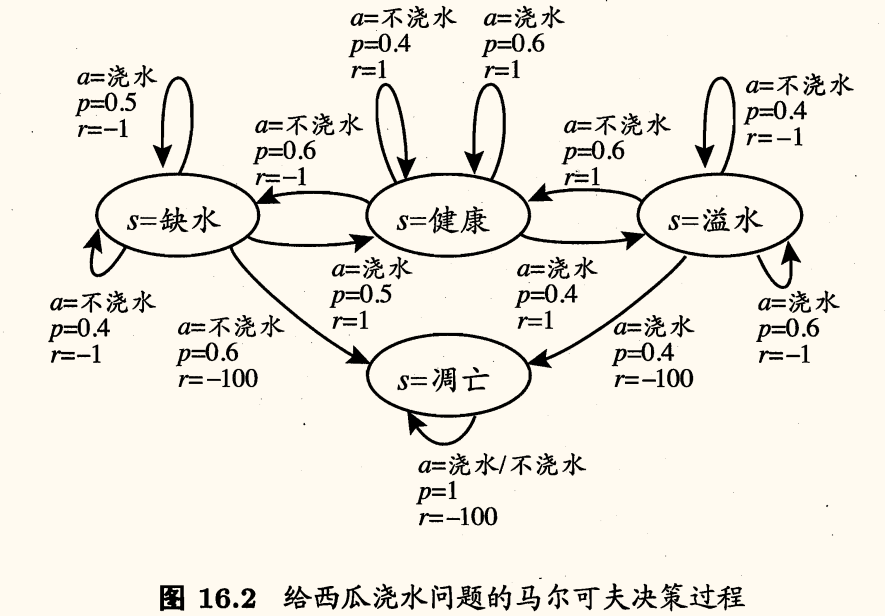
- 状态:S={健康,缺水,溢水,凋亡}
- 动作:A={浇水,不浇水}
- a 表示导致状态转移的动作
- p 表示状态转移的概率
- r 表示奖赏
需注意「机器」与「环境」的界限,例如在种西瓜任务中,环境是西瓜生长的自然世界;在下棋对弈中,环境是棋盘与对手;在机器人控制中,环境是机器人的躯体与物理世界。总之,在环境中状态的转移、奖赏的返回是不受机器控制的,机器只能通过选择要执行的动作来影响环境,也只能通过观察转移后的状态和返回的奖赏来感知环境。
机器要做的是通过在环境中不断尝试而学得一个策略 π,根据这个策略,在状态 x 下就能得知要执行的动作 a=π(x)。策略有两种表示方式:
- 确定型策略:π:X→A
- 随机性策略:π:X×A→R,π(x,a) 表示状态 x 下执行动作 a 的概率,有 ∑aπ(x,a)=1
策略的优劣取决于长期执行这一策略后得到的累积奖赏,例如某个策略使得瓜苗枯死,它的累积奖赏会很小,另一个策略种出了好瓜,它的累积奖赏会很大。在强化学习任务中,学习的目的就是要找到能使长期累积奖赏最大化的策略。
长期累计奖赏有多种计算方式,常用的有
- T 步累积奖赏:E[T1∑t=1Trt]
- γ 折扣累积奖赏:E[∑t=0∞γtrt+1]
其中 rt 表示第 t 步获得的奖赏值,γ∈[0,1] 是折扣因子,表示未来奖赏的重要性,γ 越大,未来奖赏的重要性越高。
强化学习与监督学习的对比:
- 监督学习:给有标记样本
- 强化学习:没有有标记样本,通过执行动作之后反馈的奖赏来学习
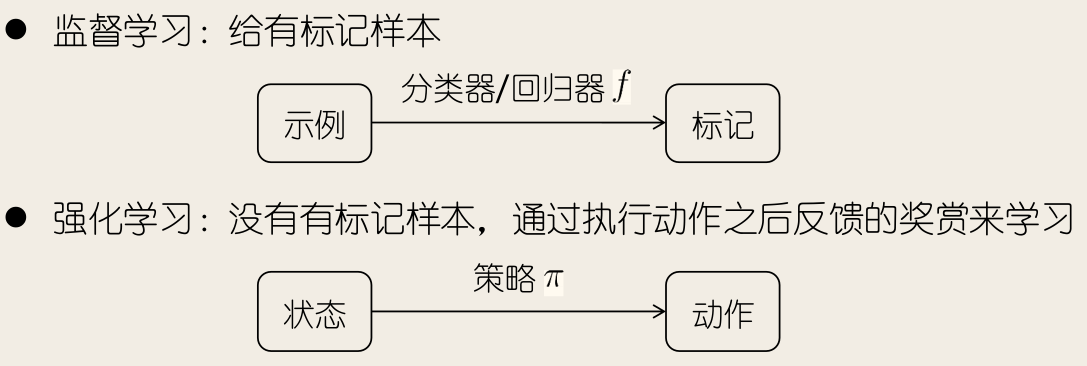
即没有人直接告诉机器在什么状态下应该做什么动作,只有等到最终结果揭晓,才能通过「反思」之前的动作是否正确来进行学习。
强化学习在某种意义上可以认为是具有「延迟标记信息」的监督学习。
强化学习问题的基本设置:
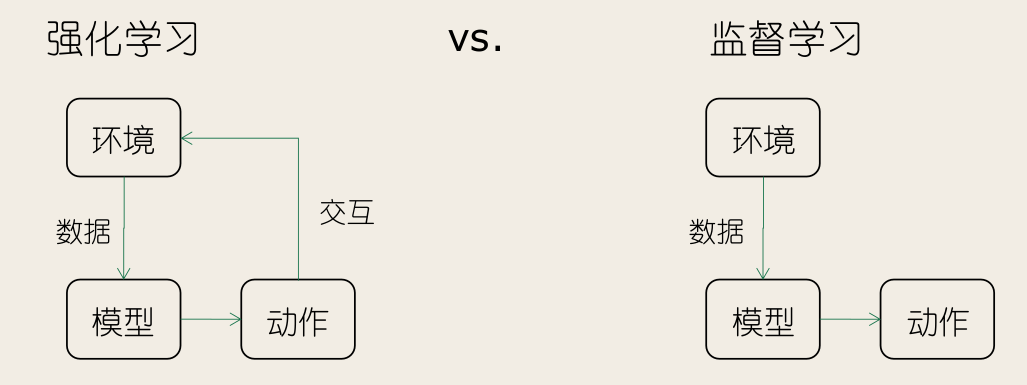
强化学习的样本可来自于与环境的交互过程。
K-摇臂赌博机
探索与利用
与一般监督学习不同,强化学习任务的最终奖赏是在多步动作之后才能观察到,这里我们不妨先考虑比较简单的情形:最大化单步奖赏,即仅考虑一步操作。需注意的是,即便在这样的简化情形下,强化学习仍与监督学习有显著不同,因为机器需通过尝试来发现各个动作产生的结果,而没有训练数据告诉机器应当做哪个动作。
欲最大化单步奖赏需考虑两个方面:
- 需知道每个动作带来的奖赏;
- 要执行奖赏最大的动作。
若每个动作对应的奖赏是一个确定值,那么尝试一遍所有的动作便能找出奖赏最大的动作。然而,更一般的情形是,一个动作的奖赏值是来自于一个概率分布,仅通过一次尝试并不能确切地获得平均奖赏值。
单步强化学习任务对应了一个理论模型「K-摇臂赌博机」(K-armed bandit, K-摇臂老虎机),如下图所示:
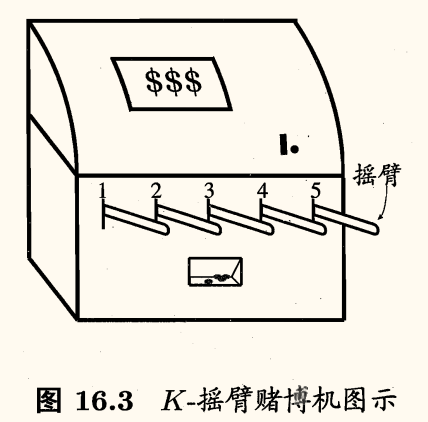
它有 K 个摇臂,赌徒在投入一个硬币后可选择按下其中一个摇臂,每个摇臂以一定概率吐出硬币,但这个概率赌徒并不知道。赌徒的目标是通过一定的策略最大化自己的奖赏,即获得最多的硬币。
若仅为获知每个摇臂的期望奖赏,则可采用「仅探索」(exploration-only)法:
- 将所有的尝试机会平均分配给每个摇臂(即轮流按下每个摇臂)
- 最后以每个摇臂各自的平均吐币概率作为其奖赏期望的近似估计
若仅为执行奖赏最大的动作,则可采用「仅利用」(exploitation-only)法:
- 按下目前最优的(即到目前为止平均奖赏最大的)摇臂
- 若有多个摇臂同为最优,则从中随机选取一个
缺陷:
- 「仅探索」法能很好地估计每个摇臂的奖赏,却会失去很多选择最优摇臂的机会;
- 「仅利用」法则相反,它没有很好地估计摇臂期望奖赏,很可能经常选不到最优摇臂。
因此,这两种方法都难以使最终的累积奖赏最大化。
事实上,探索(即估计摇臂的优劣)和利用(即选择当前最优摇臂)这两者是矛盾的,因为尝试次数(即总投币数)有限,加强了一方则会自然削弱另一方,这就是强化学习所面临的「探索-利用窘境」(Exploration-Exploitation dilemma)。
显然,欲累积奖赏最大,则必须在探索与利用之间达成较好的折中。
ϵ-贪心
ϵ-贪心法基于一个概率来对探索和利用进行折中:
- 每次尝试时,以 ϵ 的概率进行探索,即以均匀概率随机选取一个摇臂;
- 以 1−ϵ 的概率进行利用,即选择当前平均奖赏最高的摇臂(若有多个,则随机选取一个)。
令 Q(k) 记录摇臂 k 的平均奖赏。若摇臂 k 被尝试了 n 次,得到的奖赏为 v1,…,vn,则平均奖赏为
Q(k)=n1i=1∑nvi
更高效的做法是对均值进行增量时计算,即每尝试一次就立即更新 Q(k),可以避免存储所有奖赏值。初始时 Q0(k)=0,第 n 次尝试后,更新 Qn(k) 为
Qn(k)=Qn−1(k)+n1(vn−Qn−1(k))
ϵ-贪心算法描述如下:

- 若摇臂奖赏的不确定性较大,例如概率分布较宽时,则需更多的探索,此时需要较大的 ϵ 值;
- 若摇臂的不确定性较小,例如概率分布较集中时,则少量的尝试就能很好地近似真实奖赏,此时需要的 ϵ 较小。
通常令 ϵ 取一个较小的常数,如 0.1 或 0.01。
然而,若尝试次数非常大,那么在一段时间后,摇臂的奖赏都能很好地近似出来,不再需要探索,这种情形下可让 ϵ 随着尝试次数的增加而逐渐减小,例如令 ϵ=1/t。
Softmax
Softmax 算法基于当前已知的摇臂平均奖赏来对探索和利用进行折中。若各摇臂的平均奖赏相当,则选取各摇臂的概率也相当;若某些摇臂的平均奖赏明显高于其他摇臂,则它们被选取的概率也明显更高。
Softmax 算法中摇臂概率的分配基于 Boltzmann 分布
P(k)=∑i=1Kexp(τQ(i))exp(τQ(k))
其中
- Q(i) 记录当前摇臂的平均奖赏;
- τ>0 称为温度(temperature),τ 越小则平均奖赏越高的摇臂被选取的概率越高。
- τ→0 时,Softmax 趋于「仅利用」;
- τ→∞ 时,Softmax 趋于「仅探索」。
Softmax 算法描述如下:

总结
两种算法都有一个折中参数(ϵ,τ),算法性能孰好孰坏取决于具体应用问题。
对于离散状态空间、离散动作空间上的多步强化学习任务,一种直接的办法是:
- 将每个状态上动作的选择看作一个 K-摇臂赌博机问题;
- 用强化学习任务的累积奖赏来代替 K-摇臂赌博机算法中的奖赏函数,即可将赌博机算法用于每个状态;
- 对每个状态分别记录各动作的尝试次数、当前平均累积奖赏等信息,基于赌博机算法选择要尝试的动作。
然而这样的做法有很多局限,因为它没有考虑强化学习任务马尔可夫决策过程的结构。
有模型学习
考虑多步强化学习任务,本节暂且假定任务对应的马尔可夫决策过程四元组 E=⟨X,A,P,R⟩ 已知,这种情形称为「模型已知」,即机器对环境进行了建模,能在机器内部模拟出与环境相同或相似的状况。在已知模型的环境中学习称为有模型学习(model-based learning)。
此时对任意状态 x,x′ 和动作 a,在 x 状态下执行动作 a 转移到 x′ 状态的概率 Px→x′a 是已知的,该转移所带来的奖赏 Rx→x′a 也是已知的。
为了便于讨论,假设 X,A 有限。
策略评估
在模型已知时,对任意策略 π 能估计出该策略带来的期望累计奖赏。
定义:
- 状态值函数(state value function):Vπ(x) 表示从状态 x 出发,使用策略 π 所带来的累积奖赏;
- 状态-动作值函数(state-action value function):Qπ(x,a) 表示从状态 x 出发,执行动作 a 后再使用策略 π 带来的累积奖赏。
有状态值函数
⎩⎨⎧VTπ(x)Vγπ(x)=Eπ[T1t=1∑Trtx0=x],=Eπ[t=0∑∞γtrt+1x0=x],T 步累积奖赏γ 折扣累积奖赏
令 x0 表示起始状态,a0 表示起始状态上采取的第一个动作,对于 T 步累积奖赏,用 t 表示后续执行的步数,有状态-动作值函数
⎩⎨⎧QTπ(x,a)Qγπ(x,a)=Eπ[T1t=1∑Trtx0=x,a0=a],=Eπ[t=0∑∞γtrt+1x0=x,a0=a],T 步累积奖赏γ 折扣累积奖赏
MDP 的马尔可夫性质,可以得到值函数的递归形式(Bellman 等式)。对于 T 步累积奖赏有
VTπ(x)=Eπ[T1t=1∑Trtx0=x]=Eπ[T1r1+TT−1T−11t=2∑Trtx0=x]=a∈A∑π(x,a)x′∈X∑Px→x′a(T1Rx→x′a+TT−1Eπ[T−11t=1∑T−1rtx0=x′])=a∈A∑π(x,a)x′∈X∑Px→x′a(T1Rx→x′a+TT−1VT−1π(x′))
第三个等号采用了动作-状态全概率展开。
类似的,对于 γ 折扣累积奖赏有
Vγπ(x)=a∈A∑π(x,a)x′∈X∑Px→x′a(Rx→x′a+γVγπ(x′))
用上面的递归等式计算值函数,实际上就是一种动态规划算法。下面是基于 T 步累积奖赏的策略评估算法的算法描述:

对于 VTπ,可设想一直递归下去,直到最初的起点。换言之,从值函数的初始值 V0π 出发,通过一次迭代计算能计算出每个状态的单步奖赏 V1π,进而从单步奖赏出发,再一次迭代计算出每个状态的两步累积奖赏 V2π,如此循环下去,直到 T 步累积奖赏 VTπ。
对于 Vγπ,因为 γt→0,因此也能用类似的算法。算法可能会迭代很多次,需要设置一个停止准则,例如设置一个阈值 θ,如将上面算法第 4 行改为
x∈Xmax∣V(x)−V′(x)∣<θ
有了状态值函数 V,就能计算出状态-动作值函数 Q,即
⎩⎨⎧QTπ(x,a)Qγπ(x,a)=x′∈X∑Px→x′a(T1Rx→x′a+TT−1VT−1π(x′))=x′∈X∑Px→x′a(Rx→x′a+γVγπ(x′))
策略改进
对某个策略的累积奖赏进行评估后,若发现其并非最优策略,则希望对其进行改进。
理想的策略应能最大化累计奖赏
π∗=πargmaxx∈X∑Vπ(x)
一个强化学习任务可能有多个最优策略,最优策略所对应的值函 V∗ 称为最优值函数
∀x∈X:V∗(x)=Vπ∗(x)
策略空间无约束时上式的 V∗ 才是最优策略对应的值函数。
由于最优值函数的累积奖赏值已达最大,可对 Bellman 等式做一个改动:
⎩⎨⎧VT∗(x)Vγ∗(x)=a∈Amaxx′∈X∑Px→x′a(T1Rx→x′a+TT−1VT−1∗(x′))=a∈Amaxx′∈X∑Px→x′a(Rx→x′a+γVγ∗(x′))
换言之
V∗(x)=a∈AmaxQπ∗(x,a)
代入可得最优状态-动作值函数
⎩⎨⎧QT∗(x,a)Qγ∗(x,a)=x′∈X∑Px→x′a(T1Rx→x′a+TT−1VT−1∗(x′))=x′∈X∑Px→x′a(Rx→x′a+γVγ∗(x′))
上面关于最优值函数的等式,称为「最优 Bellman 等式」,唯一解是最优值函数。
最优 Bellman 等式揭示了非最优策略的改进方式:将策略选择的动作改变为当前最优的动作。
不妨令动作改变后对应的策略为 π′,改变动作的条件为 Qπ(x,π′(x))⩾Vπ(x),以 γ 折累积奖赏为例,可得递推不等式
Vπ(x)⩽Qπ(x,π′(x))=x′∈X∑Px→x′π′(x)(Rx→x′π′(x)+γVπ(x′))⩽x′∈X∑Px→x′π′(x)(Rx→x′π′(x)+γQπ(x′,π′(x′)))=…=Vπ′(x)
值函数对于策略的每一点改进都是单调递增的,因此对于当前策略 π,可将其改进为
π′(x)=a∈AargmaxQπ(x,a)
直到 π′ 与 π 一致,不再发生变化,此时找到了最优策略。
策略迭代和值改进
策略迭代(policy iteration):先进行策略评估,然后改进策略……不断迭代,直到策略收敛、不再改变为止。
下面的算法描述,基于 T 步累计奖赏策略评估,加入策略改进:

类似的可得基于 γ 折扣累积奖赏的策略迭代算法。
策略迭代算法在每次改进策略后都须重新进行评估,通常比较耗时。
策略改进与值函数改进是一致的,可将策略改进视为值函数的改善,有
⎩⎨⎧VT(x)Vγ(x)=a∈Amaxx′∈X∑Px→x′a(T1Rx→x′a+TT−1VT−1(x′))=a∈Amaxx′∈X∑Px→x′a(Rx→x′a+γVγ(x′))
于是可得到值迭代(value iteration)算法,即不再进行策略评估,而是直接对值函数进行迭代:

从上面的算法可看出,在模型已知时强化学习任务能归结为基于动态规划的寻优问题。与监督学习不同,这里并未涉及到泛化能力,而是为每一个状态找到最好的动作。
免模型学习
在现实的强化学习任务中,环境的转移概率、奖赏函数往往很难得知,甚至很难知道环境中一共有多少状态。
若学习算法不依赖于环境建模,则称为免模型学习(model-free learning)。
蒙特卡罗强化学习
困难:
- 策略无法评估
- 无法通过值函数计算状态-动作值函数
- 机器只能从一个起始状态开始探索环境
解决困难的办法
- 多次采样
- 直接估计每一对状态-动作的值函数
- 在探索过程中逐渐发现各个状态
在免模型情形下,策略迭代算法首先遇到的问题是策略无法评估,这是由于模型未知而导致无法做全概率展开。此时只能通过在环境中执行选择的动作,来观察转移的状态和得到的奖赏。
受 K-摇臂赌博机的启发,一种直接的策略评估替代方法是多次「采样」,然后求取平均累积奖赏来作为期望累积奖赏的近似,这称为蒙特卡罗强化学习。
由于采样必须为有限次数,因此该方法更适合于使用 T 步累积奖赏的强化学习任务。
另一方面,策略迭代算法估计的是状态值函数 V,最终策略是通过状态-动作值函数来获得。当模型未知时,从 V 到 Q 没有简单的转换方法。
于是将估计对象从 V 转变为 Q,即估计每一对状态-动作的值函数。
综合起来,模型未知的情形下,从初始状态出发,使用某种策略进行采样,执行该策略 T 步并获得轨迹
⟨x0,a0,r1,…,xT−1,aT−1,rT,xT⟩
然后,对轨迹中出现的每一对状态-动作,记录其后的奖赏之和,作为该状态-动作对的一次累积奖赏采样值。多次采样得到多条轨迹后,将每个状态-动作对的累积奖赏采样值进行平均,即得到状态-动作值函数的估计。
可以看出,欲较好地获得值函数的估计,就需要多条不同的采样轨迹。
然而,我们的策略有可能是确定性的,即对于某个状态只会输出一个动作,若使用这样的策略进行采样,则只能得到多条相同的轨迹。这与 K-摇臂赌博机的「仅利用」法面临相同的问题。
因此可借鉴探索与利用折中的办法,例如 ϵ-贪心法:
- ϵ 概率从所有动作中均匀随机选取一个;
- 1−ϵ 概率选择当前最优的动作。
确定性策略 π 称为原始策略,原始策略上使用 ϵ-贪心法策略记为
πϵ(x)={π(x),A 中以均匀概率选取的动作,概率为 1−ϵ概率为 ϵ
对于最大话值函数的原始策略 π=argmaxaQ(x,a),假设只有一个最优动作,ϵ-贪心策略 πϵ 中,当前最优动作被选中的概率是 1−ϵ+∣A∣ϵ,非最优动作被选中的概率是 ∣A∣ϵ,于是每个动作都有可能被选取,多次采样会产生不同的采样轨迹。
「同策略」(on-policy)蒙特卡罗强化学习算法描述如下:

算法中奖赏均值采用增量式计算,每采样出一条轨迹,就根据该轨迹涉及的所有「状态-动作」对来对值函数进行更新。
同策略蒙特卡罗强化学习算法最终产生的是 ϵ-贪心策略。但引入 ϵ-贪心是为了便于策略评估,使用策略时不需要 ϵ-贪心。实际上我们希望改进的是原始(非 ϵ-贪心)策略,可以仅在策略评估时引入 ϵ-贪心,而在策略改进时改进原始策略。
不妨用两个不同的策略 π,π′ 产生采样轨迹,两者的区别在于每个「动作-状态对」被采样的概率不同。
可从概率分布 p 上的采样 {x1,…,xm} 估计 f 的期望
E^[f]=m1i=1∑mf(xi)
若引入另一个分布 q,f 在概率分布 p 下的期望可等价写为
E[f]=∫xq(x)q(x)p(x)f(x)dx
上式可看作 q(x)p(x)f(x) 在分布 q 下的期望,因此通过在 q 上的采样 {x1′,…,xm′} 可估计为
E^[f]=m1i=1∑mq(xi′)p(xi′)f(xi′)
回到问题来,使用策略 π 的采样轨迹来评估策略 π,实际上就是对累积奖赏估计期望
Q(x,a)=m1i=1∑mri
若改用策略 π′ 的采样轨迹评估策略 π,则仅需对累积奖赏加权,即
Q(x,a)=m1i=1∑mPiπ′Piπri
其中 Piπ,Piπ′ 分别表示两个策略产生第 i 条轨迹的概率。
对于给定的一条轨迹 (x0,a0,r1,…,xT−1,aT−1,rT,xT),策略 π 产生该轨迹的概率为
Pπ=i=0∏T−1π(xi,ai)Pxi→xi+1ai
虽然这里使用了环境的转移概率 Pxi→xi+1ai,但实际上 E^ 只需要两个策略概率的比值
Pπ′Pπ=i=0∏T−1π′(xi,ai)π(xi,ai)
若 π 为确定性策略而 π′ 是 π 的 ϵ-贪心策略,则 π(xi,ai) 始终为 1,π′(xi,ai) 为 ∣A∣ϵ 或 1−ϵ+∣A∣ϵ,于是就能对策略 π 进行评估。
下面即「异策略」(off-policy)蒙特卡罗强化学习算法描述:

时序差分学习
蒙特卡罗强化学习的缺点就是「低效」:
- 求平均时以「批处理式」进行
- 在一个完整的采样轨迹完成后才对状态-动作值函数进行更新
克服缺点的办法就是时序差分(temporal difference, TD)学习。
时序差分学习增量式地进行状态-动作值函数的更新,采用 ϵ-贪心法有:
- 同策略:Sarsa 算法
- 异策略:Q-学习(Q-learning)
Sarsa 算法描述如下:

Q-学习算法描述如下:

值函数近似
前面假定状态空间离散(有限),若状态空间连续(无限),则无法使用表格来存储值函数,值函数不再是关于状态的「表格值函数」(tabular value function)。
解决方法是「值函数近似」(value function approximation),即用一个函数来近似值函数。
为简便起见,假定状态空间 X=Rn,首先考虑线性近似,假定行为空间有限,则将值函数表达为状态的线性函数
Vθ(x)=θ⊺x
其中 θ∈Rn 是参数向量,x∈Rn 是状态向量。
用最小二乘误差来度量学到的值函数和真实的值函数 Vπ 之间的近似程度
εθ=Ex∼π[(Vπ(x)−Vθ(x))2]
用梯度下降法更新参数向量,求解优化问题。
状态-动作值函数的线性近似则为
Qθ(x,a)=θ⊺(x,a)
其中 a=(0,…,1,…,0)。
非线性值函数的近似有几种方法,如:
模仿学习
强化学习任务中多步决策的搜索空间巨大,基于累积奖赏来学习很多步之前的合适决策非常困难。
但在现实任务中,往往能得到人类专家的决策过程范例,例如在种瓜任务上能得到农业专家的种植过程范例。从这样的范例中学习,称为模仿学习(imitation learning)。
直接模仿学习
缓解方法是直接模仿人类专家的状态-动作对来学习策略,即直接模仿学习。
这相当于告诉机器在什么状态下应该选择什么动作,引入了监督信息来学习策略。
步骤:
- 利用专家的决策轨迹,构造数据集 D,其中状态作为特征,动作作为标记;
- 利用数据集 D,使用分类/回归算法即可学得策略;
- 将学得策略作为初始策略;
- 策略改进,从而获得更好的策略。
假定人类专家决策轨迹数据为 {τ1,…,τm},每条轨迹包含状态和动作序列
τi=⟨s1i,a1i,…,sni+1i⟩
其中 ni 为第 i 条轨迹中的转移次数。
有了这样的数据,就相当于告诉机器在什么状态下应选择什么动作,于是可利用监督学习来学得符合人类专家决策轨迹数据的策略。
可将所有轨迹上的所有「状态-动作对」抽取出来,构造出一个新的数据集合
D={(s1,a1),…,(s∑i=1mni,a∑i=1mni)}
即把状态作为特征,动作作为标记。
然后,对这个新构造出的数据集合 D 使用分类(对于离散动作)或回归(对于连续动作)算法即可学得策略模型。
学得的这个策略模型可作为机器进行强化学习的初始策略,再通过强化学习方法基于环境反馈进行改进,从而获得更好的策略。
逆强化学习
在很多任务中,设计奖赏函数往往相当困难,从人类专家提供的范例数据中反推出奖赏函数有助于解决该问题,这就是逆强化学习(inverse reinforcement learning)。
基本思想:寻找某种奖赏函数使得范例数据是最优的,然后即可使用这个奖赏函数来训练强化学习策略。
逆强化学习中,我们知道状态空间 X、动作空间 A,并且与直接模仿学习类似,有一个决策轨迹数据集 {τ1,…,τm}。
不妨假设奖赏函数能表达为状态特征的线性函数,即 R(x)=w⊺x,于是策略 π 的累积奖赏可写为
ρπ=E[t=0∑+∞γtR(xt)π]=E[t=0∑+∞γtw⊺xtπ]=w⊺E[t=0∑+∞γtxtπ]
即状态向量加权和的期望与系数 w 的内积。
将状态向量的期望 E[∑t=0+∞γtxt∣π] 记为 xˉπ,因为获得其需要求期望,可以使用蒙特卡罗方法通过采样近似期望,而范例轨迹数据集可看作最优策略的一个采样,于是可将每条范例轨迹上的状态向量加权和再平均,记为 xˉ∗。
对于最优奖赏函数 R(x)=w∗⊺x 和其他任意策略产生的 xˉπ,有
w∗⊺xˉ∗−w∗⊺xˉπ=w∗⊺(xˉ∗−xˉπ)⩾0
若能对所有策略计算出 (xˉ∗−xˉπ),则可找到最优奖赏函数,即解得
w∗=wargmaxπminw⊺(xˉ∗−xˉπ)s.t.∥w∥⩽1
然而我们难以获得所有策略。一个较好的办法是从随机策略开始,迭代地求解更好的奖赏函数,基于奖赏函数获得更好的策略,直至最终获得最符合范例轨迹数据集的奖赏函数和策略。
算法描述如下图所示:

















