条件概率
The probability of A is p, given that B occurs. 即在事件 B 发生的条件下,事件 A 发生的概率 p,称为条件概率。
对于离散均匀分布的情况
p=∣B∣∣A∩B∣=∣B∣/∣Ω∣∣A∩B∣/∣Ω∣=Pr(B)Pr(A∩B)
令 A 是一个事件,B 是一个非零概率事件,即 Pr(B)>0,则 A 在 B 条件下的概率(conditional probability)定义为
Pr(A∣B)=Pr(B)Pr(A∩B)
条件概率是概率
- 样本空间是 B
- ΣB={A∩B∣A∈Σ} 是 σ-代数
- 概率测度 Pr(⋅∣B) 满足概率公理
辛普森悖论是指一个总体中的两组数据分别满足某一规律,但是当这两组数据合并后,这一规律却被打破的现象。
在概率论中,可以构造事件 A,B 与样本空间 Ω 的划分 C1,C2,⋯,Cn 使得
- 对于每个 Ci,B 的发生对 A 有正向影响
- Pr(A∣B∩Ci)>Pr(A∣Bc∩Ci) 对任意 i 成立
- 但总体上,B 的发生对 A 有负向影响
- Pr(A∣B)<Pr(A∣Bc)
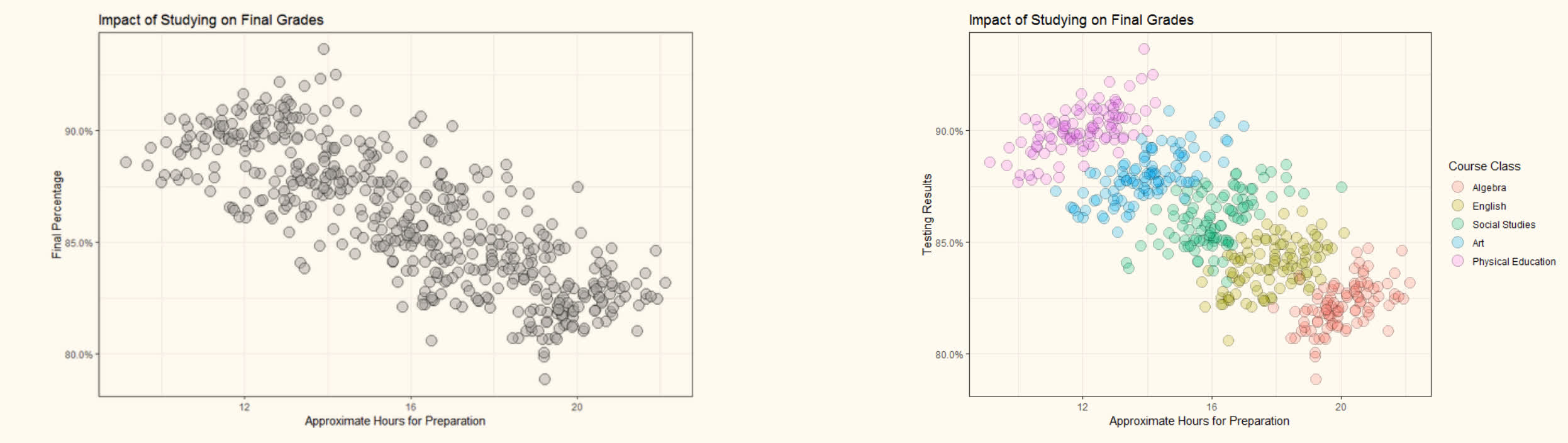
其他例子:
条件概率法则(Laws for Conditional Probability)
链式法则
链式法则(Chain Rule)
对于任意事件 A1,A2,⋯,An,有
Pr(i=1⋂nAi)=i=1∏nPr(Aij<i⋂Aj)
证明
Pr(i=1⋂nAi)=Pr(⋂i=1n−1Ai)Pr(⋂i=1nAi)⋅Pr(⋂i=1n−2Ai)Pr(⋂i=1n−1Ai)⋯Pr(A1)Pr(A1∩A2)⋅Pr(A1)
链式法则,又称为 General Product Rule 或 Law of Successive Conditioning。
考虑均匀随机映射 f:[n]→[m],有 f 为 1-1 映射(双射)的概率
Pr[f is 1-1]=mnm!/(m−n)!=i=1∏n(1−mi−1)
中间的式子可以这样看:一共有 mn 种映射,假设 [n] 就按 1,…,n 排列,为了要双射,需从 [m] 中选择 n 个元素,然后排列,即 m!/(m−n)!。
最后的式子可以看成化简的结果,也可以看成链式法则的计算。即在 j<i 都已经是双射的情况下,第 i 个元素不与前面的 i−1 个元素重复的概率。
Balls-into-bins 模型中,有 n 个球随机放入 m 个盒子,每个盒子最多放一个球的概率为 ϵ,其中 n≈2mln(1/ϵ)。
Pr[每个球入一个空盒]=i=1∏nPr[球 i 入空盒∣每个球 j<i 在空盒]=i=1∏n(1−mi−1)≈exp(−i=1∑nmi−1)≈exp(−2mn2)
全概率法则
全概率法则(Law of Total Probability)
对于任意事件 A 和样本空间 Ω 的划分 B1,B2,⋯,Bn,有
Pr(A)=i=1∑nPr(A∩Bi)=i=1∑nPr(A∣Bi)Pr(Bi)
证明
A∩B1,A∩B2,⋯,A∩Bn 互不相交,同时 A=i=1⋃n(A∩Bi)。
从而有 Pr(A)=i=1∑nPr(A∩Bi)。
而 Pr(A∩Bi)=Pr(A∣Bi)Pr(Bi)。
三门问题
赌徒破产(Gambler's Ruin, 一维对称随机游走):一个赌徒玩一个公平的游戏,每一步他抛一枚硬币,正面得一分,反面失一分。他以 k 分开始游戏,会一直玩直到分数为 0(失败)或 n(胜利)。那么他最终破产的概率是多少?
解答
记事件
令 Prk 是赌徒以 k 分开始游戏时最终破产的概率分布,有
Prk(A)=21Prk(A∣B)+21Prk(A∣Bc)=21Prk+1(A)+21Prk−1(A)
即
Prk(A)=⎩⎨⎧21(Prk+1(A)+Prk−1(A))10if 0<k<nif k=0if k=n
注意到
21(Prk+1(A)−Prk(A))=21(Prk(A)−Prk−1(A))
即 Prk(A) 是一个等差数列,从而有 Prk(A)=1−nk。
贝叶斯定律
贝叶斯定律(Bayes' Law)
对于任意事件 A 和样本空间 Ω 的划分 B1,B2,⋯,Bn,有
Pr(Bi∣A)=Pr(A)Pr(Bi)Pr(A∣Bi)=j=1∑nPr(A∣Bj)Pr(Bj)Pr(A∣Bi)Pr(Bi)

