概率空间

样本空间

样本空间（sample space）$\Omega$ 是一个集合，包含一次试验的所有可能结果。

每个 $\omega \in \Omega$ 称为一个样本（sample）或基本事件（elementary event）。

离散概率空间

对于离散概率空间（即 $\Omega$ 有限或可数无穷）：

• 概率质量函数（probability mass function, pmf）$p\colon \Omega \to [0, 1]$ 满足 $\displaystyle \sum_{\omega \in \Omega} p(\omega) = 1$；
• 事件 $A \subseteq \Omega$ 的概率（probability）定义为 $\displaystyle \Pr(A) = \sum_{\omega \in A} p(\omega)$。即 $\Pr\colon 2^\Omega \to [0, 1]$。

样本空间与事件

事件（event）满足：

• $\empty, \Omega$ 都是事件（称为不可能事件和必然事件）；
• 若 $A$ 是事件，则 $A^c$ 也是事件；
• 若 $A_1, A_2, \cdots$ 是事件，则 $\bigcup_i A_i$ 也是事件。

$\sigma$-代数

$\Omega$ 的子集族 $\Sigma \subseteq 2^{\Omega}$ 称为 $\sigma$-代数（$\sigma$-algebra）或 $\sigma$-域（$\sigma$-field）满足：

• $\empty \in \Sigma$；
• $A \in \Sigma \implies A^c \in \Sigma$；
• $A_1, A_2, \cdots \in \Sigma \implies \bigcup_i A_i \in \Sigma$。

概率空间的经典例子

• 古典概型（classic probability）：离散均匀分布。对于有限样本空间 $\Omega$，任意的结果 $\omega \in \Omega$ 都有相同的概率。则对于任意事件 $A \subseteq \Omega$，有 $\Pr(A) = \dfrac{|A|}{|\Omega|}$。
• 几何概型（geometric probability）：连续概率空间使得，对于任意事件 $A \subset \Sigma$，有 $\Pr(A) = \dfrac{\operatorname{Vol}(A)}{\operatorname{Vol}(\Omega)}$。

几何概型的例子有蒲丰投针问题（Buffon's Needle Problem），这个三年前有写过短篇笔记，方法比较粗糙，格式也比较差劲，但作为一段历史还是放在下面。

2021 年 7 月 4 日

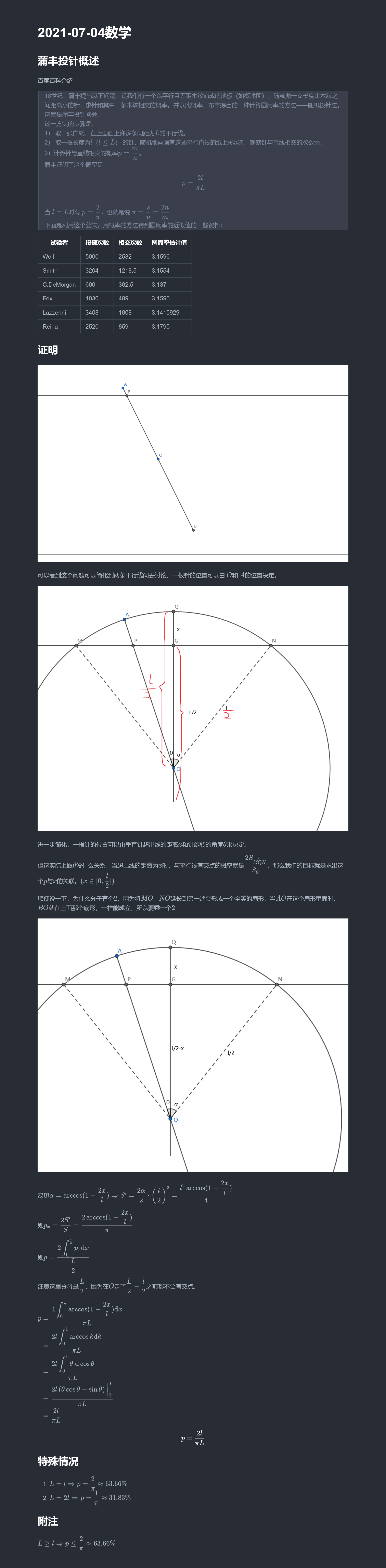
下面是课件上的证明，记号有所不同。

记事件 $A = \left\lbrace (x, y) \in [0, \pi] \times \left[0, \dfrac{d}{2}\right] \middle| y \le \dfrac{l}{2} \sin x \right\rbrace$，则

$$\begin{aligned} \Pr(A) &= \dfrac{\operatorname{Vol}(A)}{\operatorname{Vol}(\Omega)} \\ &= \dfrac{2}{d \pi} \int_0^{\pi} \dfrac{l}{2} \sin x \d x\\ &= \dfrac{2l}{d \pi} \end{aligned}$$

概率空间

一般而言，三元组 $(\Omega, \Sigma, \Pr)$ 称为一个概率空间（probability space），若：

• 令 $\Sigma \subseteq 2^{\Omega}$ 为 $\sigma$-代数；
• 概率测度（probability measure），亦称概率律（probability law），是一个函数 $\Pr\colon \Sigma \to [0, 1]$ 满足：
  • 归一性/标准化（unitary/normalized）：$\Pr(\Omega) = 1$；
  • $\sigma$-可加性（$\sigma$-additive）：若 $A_1, A_2, \cdots \in \Sigma$ 两两互斥（disjoint），则 $\Pr\left(\bigcup_i A_i\right) = \sum_i \Pr(A_i)$。

可从上面的概率空间公理推导出以下性质：

• $\Pr(\empty) = 0$（$\Pr(A) > 0 \implies A \neq \empty$）；
• $\Pr(A^c) = 1 - \Pr(A)$；
• $\Pr(A \backslash B) = \Pr(A) - \Pr(A \cap B)$；
• $A \subseteq B \implies \Pr(A) \le \Pr(B)$；
• $\Pr(A \cup B) = \Pr(A) + \Pr(B) - \Pr(A \cap B)$。

仅从上面的叙述似乎感觉不到这个定义的意义所在，下面通过两个例子阐释一下我的理解。

1. 「任意一个自然数是偶数的概率为 $\dfrac{1}{2}$」
2. 「$[0, 1]$ 中随机抽取一个实数是有理数的概率为 $0$」

解释

第一个是错误的，甚至是 not even wrong 的。因为无法定义这样的「均匀分布」。

若是要均匀分布，为其中每一个自然数分配一个概率 $p$，那么我们有

$$\sum_{n=1}^\infty p = 1$$

这显然是不可能的。因此，我们无法定义一个均匀分布在自然数上的概率测度。

第二个是正确的。一开始我还有疑问，为什么这个就不会出现像上面那样，每个数概率为 $0$，但是和为 $1$ 的无良定义的情况呢？于是我去问了 ChatGPT 得到了满意的答案，下面就是我的理解了：

原因就是上面的概率测度。面对不可数集时，常常使用连续概率分布，这时的概率并不是像之前的例子一样是离散的，在这种情况下，概率分布不是通过单个点的概率来处理，而是通过区间的长度来计算。因此「均匀分布」是有合理的定义在的。

存在不可数的 $[0, 1]$ 的子集，使得其概率为 $0$。答案是康托尔集。

并集界

并集界（Union bound, 布尔不等式）

对任意事件 $A_1, A_2, \cdots, A_n \in \Sigma$，有

$$\Pr\left(\bigcup_{i=1}^n A_i\right) \le \sum_{i=1}^n \Pr(A_i)$$

Balls into bins 问题

将 $n$ 个球随机扔到 $n$ 个盒中，$k$ 是盒中球最多的个数，则 $k$ 高概率（with high probability, w.h.p., 以 $1 - O(1/n)$ 概率）是 $O\left( \dfrac{\ln n}{\ln \ln n} \right)$。

证明

记

• 事件 $A$：存在盒接受到不少于 $k$ 个球（$k$ 是待定常数）
• 事件 $A_i$：盒-$i$ 接受到不少于 $k$ 个球

并集界有

$$\Pr(A) = \Pr\left( \bigcup_{i=1}^n A_i \right) \le \sum_{i=1}^n \Pr(A_i) \le \dfrac{1}{n}$$

因为此时有 $\Pr(A^c) \ge 1 - \dfrac{1}{n}$。

对于任意 $S \in \dbinom{[n]}{k}$（其中 $[n] = \left\lbrace 1, 2, \cdots, n \right\rbrace$），记事件 $A_{i, S}$ 为盒-$i$ 接受到的球都是 $S$ 中的球。则根据并集界有

$$\begin{aligned} \Pr(A_i) \end{aligned}$$

容斥原理

容斥原理（Principle of Inclusion-Exclusion）

对任意事件 $A_1, A_2, \cdots, A_n \in \Sigma$，有

$$\begin{aligned} \Pr\left(\bigcup_{i=1}^n A_i\right) &= \sum_{i=1}^n \Pr(A_i) - \sum_{i < j} \Pr(A_i \cap A_j) + \sum_{i < j < k} \Pr(A_i \cap A_j \cap A_k) -\\ &= \sum_{\substack{S \subseteq \left\lbrace 1, 2, \cdots, n \right\rbrace\\ S \ne \empty}} (-1)^{|S| - 1} \Pr\left(\bigcap_{i \in S} A_i\right) \end{aligned}$$

布尔-邦费罗尼不等式（Boole-Bonferroni inequality）

由布尔不等式可得事件并集的上下界。

对任意事件 $A_1, A_2, \cdots, A_n \in \Sigma$ 与任意 $k > 0$，有

$$\sum_{\substack{S \subseteq \left\lbrace 1, 2, \cdots, n \right\rbrace\\ 1 \le |S| \le 2k}} (-1)^{|S| - 1} \Pr\left(\bigcap_{i \in S} A_i\right) \le \Pr\left(\bigcup_{i=1}^n A_i\right) \le \sum_{\substack{S \subseteq \left\lbrace 1, 2, \cdots, n \right\rbrace\\ 1 \le |S| \le 2k+1}} (-1)^{|S| - 1} \Pr\left(\bigcap_{i \in S} A_i\right)$$

错排问题（Derangement）

随机排列 $\pi\colon [n] \xrightarrow{\text{1-1 onto}} [n]$ 不存在不动点的概率。

解答

令 $A_i$ 是 $\pi(i) = i$ 的事件，有

$$\begin{aligned} \Pr\left( \bigcup_{i=1}^n A_i \right) &= \sum_{k=1}^n \sum_{S \in \binom{[n]}{k}} (-1)^{k-1} \Pr\left( \bigcap_{i \in S} A_i \right)\\ &= \sum_{k=1}^n \sum_{S \in \binom{[n]}{k}} (-1)^{k-1} \dfrac{(n - |S|)!}{n!}\\ &= \sum_{k=1}^n \dbinom{n}{k} (-1)^{k-1} \dfrac{(n-k)!}{n!}\\ &= -\sum_{k=1}^n \dfrac{(-1)^{k}}{k!} \end{aligned}$$

则

$$\begin{aligned} \Pr[\pi \text{ 没有不动点}] &= \Pr\left( \bigcap_{i=1}^n A_i^c \right)\\ &= 1 - \Pr\left( \bigcup_{i=1}^n A_i \right)\\ &= 1 + \sum_{k=1}^n \dfrac{(-1)^{k}}{k!}\\ &= \sum_{k=0}^n \dfrac{(-1)^{k}}{k!}\\ &\to \dfrac{1}{\e}\quad (n \to \infty ) \end{aligned}$$

概率测度的连续性（continuity of probability measures）*

记 $A_1 \subseteq A_2 \subseteq \cdots$ 是一个递增的事件序列，并记 $A$ 是它们的极限

$$A = \bigcup_{i=1}^{\infty } = \lim_{n \to \infty} A_n$$

于是

$$\Pr(A) = \lim_{n \to \infty} \Pr(A_n)$$

证明

将 $A$ 表示为不相交的并集

$$A = A_1 \uplus (A_2 \backslash A_1) \uplus (A_3 \backslash A_2) \uplus \cdots$$

于是

$$\begin{aligned} \Pr(A) &= \Pr(A_1) + \sum_{i=1}^{\infty } \Pr(A_{i+1} \backslash A_i)\\ &= \Pr(A_1) + \lim_{n\to \infty } \sum_{i=1}^{n-1} [\Pr(A_{i+1} - \Pr(A_i))]\\ &= \lim_{n\to \infty } \Pr(A_n) \end{aligned}$$

类似地，记 $B_1 \supseteq B_2 \supseteq \cdots$ 是一个递减的事件序列，并记 $B$ 是它们的极限

$$B = \bigcap_{i=1}^{\infty } = \lim_{n \to \infty} B_n$$

于是

$$\Pr(B) = \lim_{n \to \infty} \Pr(B_n)$$

证明

考虑它们的补集 $B_n^c$，有 $B_1^c \subseteq B_2^c \subseteq \cdots$，于是这是一个递增的事件序列，根据上面的结论得证。

几乎从不和几乎必然事件*

• 一个事件 $A \in \Sigma$ 称为 null(几乎从不)，若 $\Pr(A) = 0$；
  • null 事件并不一定是 impossible(不可能) 事件 $\empty$
• 一个事件 $A \in \Sigma$ almost sure(a.s.,几乎必然) 发生，若 $\Pr(A) = 1$；
  • 一个事件 a.s. 发生 事件并不一定是 certain(必然) 事件 $\Omega$
• 一个概率空间称为 complete，若 $\Sigma$ 包含所有 null 事件的补集。
  • 不失一般性，我们仅考虑 complete 概率空间（因为若考虑 incomplete 的，可以将其 complete 而不改变其概率）