基本数据结构

A data structure(数据结构) is a way to store and organize data in order to facilitate access and modifications.

Abstract Data Type

A data structure usually provides an interface. Often, the interface is also called an Abstract Data Type (ADT).

An ADT specifies what a data structure "can do" and "should do", but not "how to do" them.

An ADT is a logical description, and a data structure is a concrete implementation.

The Queue ADT

Queue

The Queue(队列) ADT represents a collection of items to which we can add items and remove the next item.

• Add(x): Add $x$ to the queue.
• Remove(): Remove the next item $y$ from queue, return $y$.

The queuing discipline decides which item to be removed.

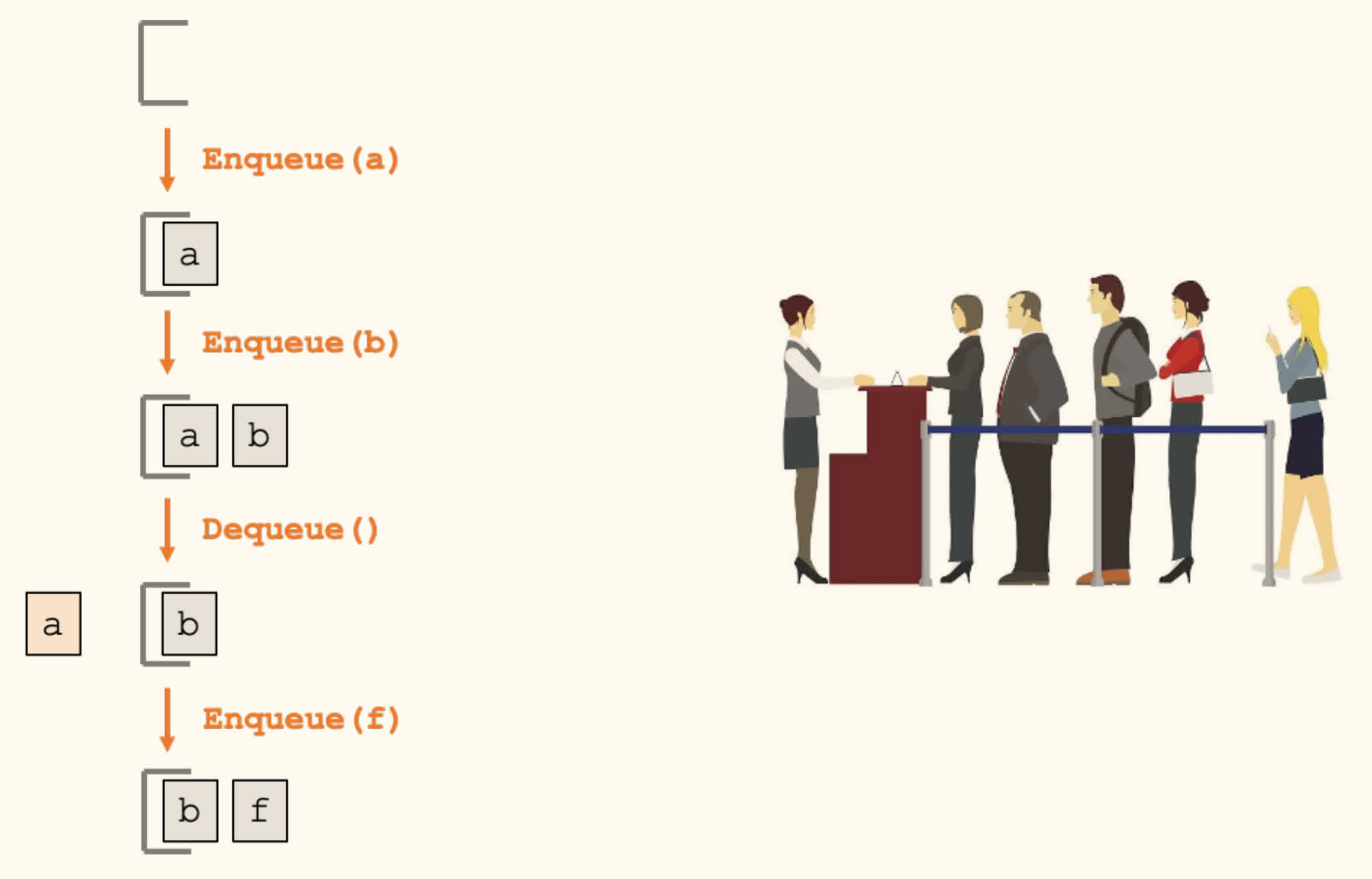
FIFO Queue

The first-in-first-out (FIFO) queuing discipline: items are removed in the same order they are added.

• Add(x) or Enqueue(x): Add $x$ to the end of the queue.
• Remove() or Dequeue(): Remove the first item from the queue.

LIFO Queue: Stack

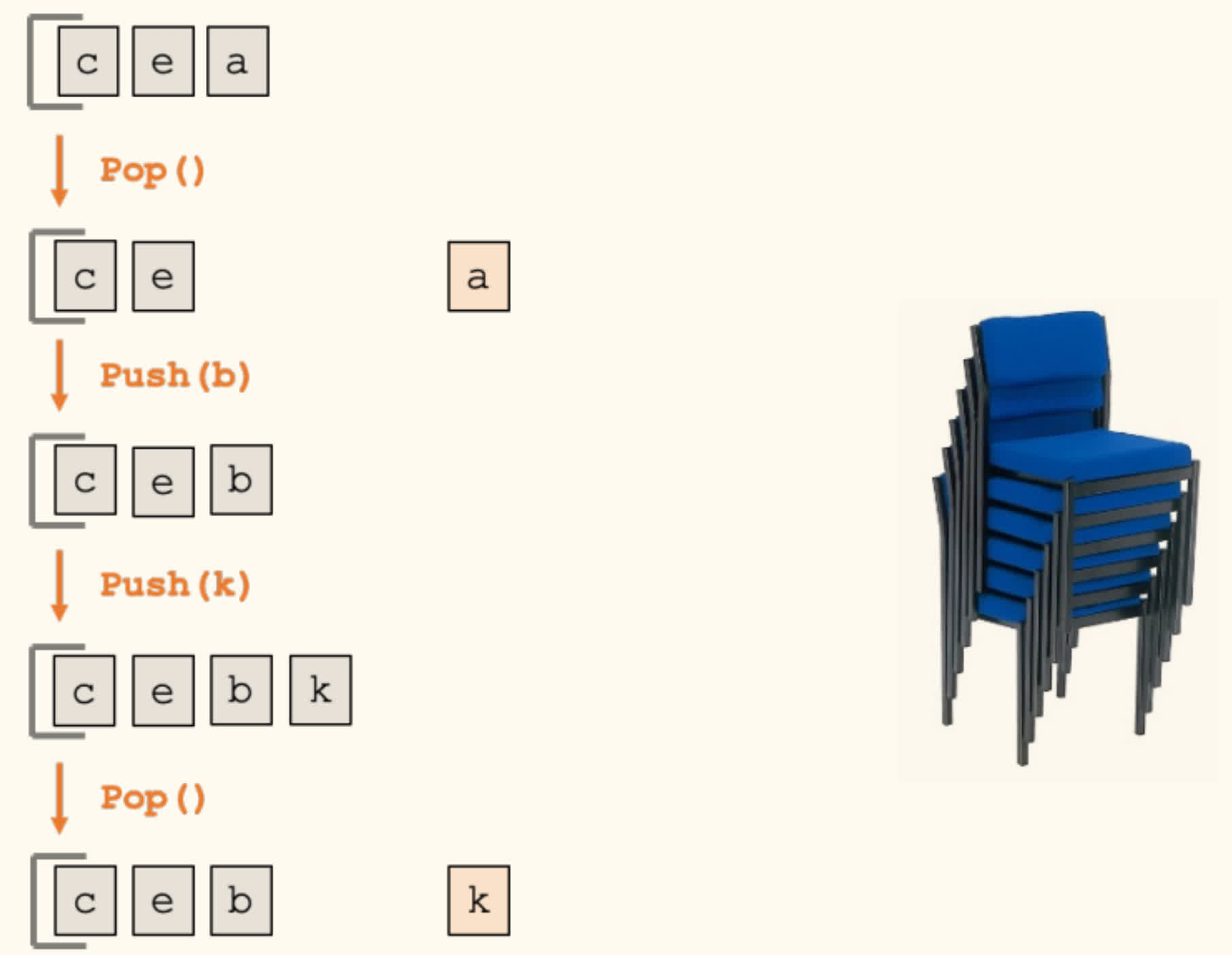
The last-in-first-out (LIFO) queuing discipline: items are removed in the reverse order they are added.

• Add(x) or Push(x): Add $x$ to the top of the stack.
• Remove() or Pop(): Remove the top item from the stack.

The Deque ADT

The Deque(双端队列, Double-Ended Queue) ADT represents a sequence of items with a front and a back, which supports the following operations:

• AddFirst(x): Add $x$ to the front of the queue.
• AddLast(x): Add $x$ to the back of the queue.
• RemoveFirst(): Remove the first item $y$ from the queue, return $y$.
• RemoveLast(): Remove the last item $y$ from the queue, return $y$.

A DEQUE is a generalization of both the FIFO Queue and LIFO QUEUE (STACK).

1. DEQUE can implement FIFO QUEUE:
   • Enqueue(x): AddFirst(x)
   • Dequeue(): RemoveFirst()
2. DEQUE can implement LIFO QUEUE (STACK):
   • Push(x): AddLast(x)
   • Pop(): RemoveLast()

The List ADT

A List(列表) is a sequence of items $x_1, x_2, \cdots, x_n$, which supports the following operations:

• Size(): return $n$, the length of the list
• Get(i): return $x_i$
• Set(i, x): set $x_i$ to $x$
• Add(i, x): set $x_{j+1} = x_{j}$ for $n \ge j \ge i$, then set $x_i = x$, increase list size by $1$
• Remove(i): set $x_{j} = x_{j+1}$ for $n - 1 \ge j \ge i$, decrease list size by $1$

LIST can implement DEQUE:

• AddFirst(x): Add(1, x)
• AddLast(x): Add(Size() + 1, x)
• RemoveFirst(): Remove(1)
• RemoveLast(): Remove(Size())

Array

ArrayList

Using array to implement LIST, ArrayList:

• Size(): $\Theta(1)$ (Use a variable size to store the size)
• Get(i): $\Theta(1)$
• Set(i, x): $\Theta(1)$
• Add(i, x): $\Theta(1)$ to $\Theta(n)$
• Remove(i): $\Theta(1)$ to $\Theta(n)$

Queries, Updates and Modifications at end are fast, but Modifications at front or middle are slow.

Therefore, ARRAYLIST is good for STACK, cos Push and Pop are fast. But not good for FIFO QUEUE and DEQUE, cos Enqueue and Dequeue are slow.

ArrayDeque

Using circular array to implement Deque, ArrayDeque:

Move head and tail pointer instead of moving elements.

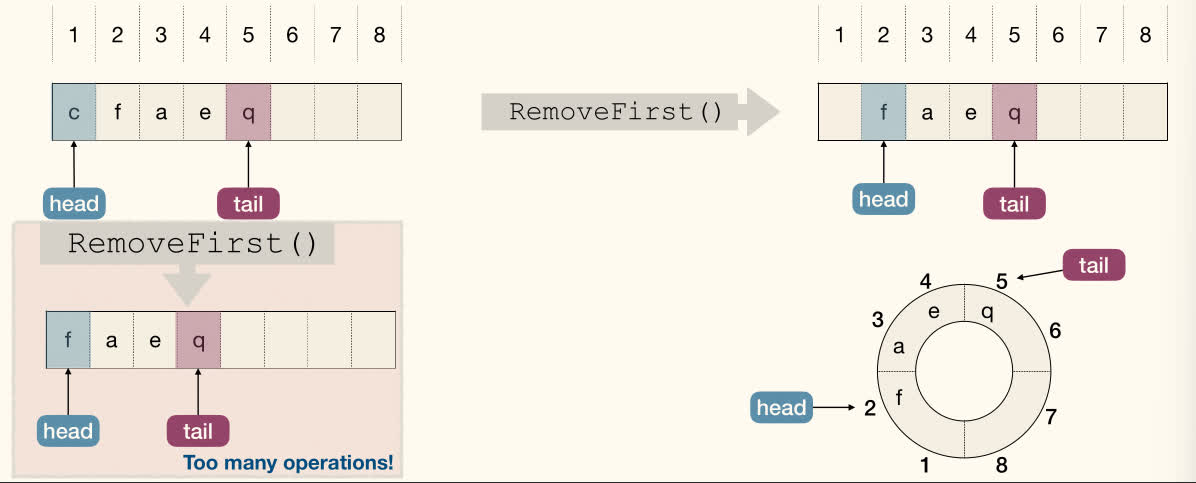
Use modular arithmetic(取模运算) to "wrap around" at both ends.

• AddLast(x): A[tail := (tail % N) + 1] := x
• RemoveLast(x): tail := (tail = 1) ? N : tail - 1
• AddFirst(x): A[head := (head = 1) ? N : head - 1] := x
• RemoveFirst(x): head := (head % N) + 1

Queries, Updates and Modifications at both front and end are fast (All of these operations are $O(1)$), but still slow at middle.

ARRAYDEQUE is good for STACK, FIFO QUEUE and DEQUE, but can be slow for some LIST operations.

When the array is full?

When the array is full, we can resize the array: Create a new array of greater size and copy the elements of the original array into it.

So, how large?

Suppose we have array with initial capacity being $1$, then insert $N$ items.

The first category of resizing is to have one additional cell every time, which requires $1 + 2 + 3 + \cdots + N = \Theta(N^2)$ copy operations.

The second category of resizing is to double the size every time, which requires $1 + 2 + 4 + \cdots + 2^{k-1} = \Theta(N)$ copy operations (For simplicity, we assume $N = 2^k$).

We could of course do better if we multiplied the size of the array by an even larger value, but then there would likely be a lot more unused cells in the array on average (consider the case that resizing happens infrequently).

Amortized analysis(平摊分析)

Starting from an empty data structure, average running time per operation over a worst-case sequence of operations.

Thus, if resizing by one more cell each time, the amortized complexity is $\Theta(n)$ for each operation. If resizing by doubling space each time, the amortized complexity is $\Theta(1)$ for each operation.

When to shrink array?

When shrinking an array, we allocate a new array with smaller capacity, and then copy necessary items from the original array into the new array, and abandon the old array.

• When pop() each time, we shrink the array by 1 less cell?
• When the array is one-half full, we shrink the array to the halve size?
  • Since, if now we add just one element, we need to resize the array by doubling the size, and then pop one element, we should shrink it back to the halve size. When pushes and pops come with relatively equal frequency, it will be too expensive! This is called Thrashing problem.

Usually, we shrink the array to half size when the array is one-quarter ($\dfrac{1}{4}$) full.

After all, by doing this we ensure that the array holding the contents of our stack will always be between $25\%$ and $100\%$ full!

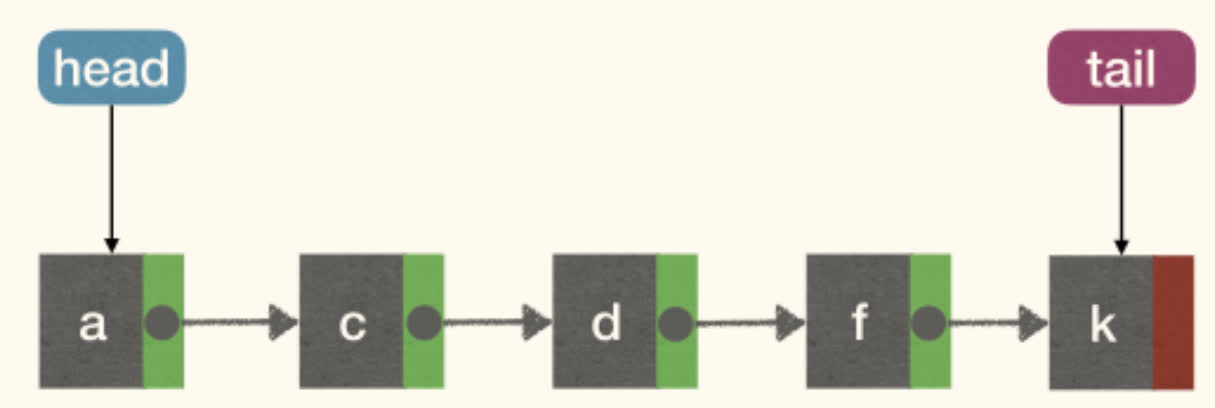
LinkedList

The list operations implemented by LinkedList:

• Size(): $\Theta(1)$
• Get(i): $\Theta(1)$ to $\Theta(n)$
• Set(i, x): $\Theta(1)$ to $\Theta(n)$
• Add(i, x): $\Theta(1)$ to $\Theta(n)$
• Remove(i): $\Theta(1)$ to $\Theta(n)$

LINKEDLIST is good for STACK (Push and Pop at head) and FIFO QUEUE (Enqueue at tail and Dequeue at head), but not good for DEQUE, cos RemoveLast can be slow.

DLinkedList (Doubly-Linked List)

DLINKEDLIST is good for STACK, FIFO QUEUE, and DEQUE; but can be slow for some LIST operations.

• AddFirst(x):

  x.next := head
  if head != NULL:
      head.prev := x
  head := x
  x.prev := NULL

However, if head is NULL, we need to update tail as well.

Since there are similar operations for head and tail, and need to consider boundary conditions, we can connect them.

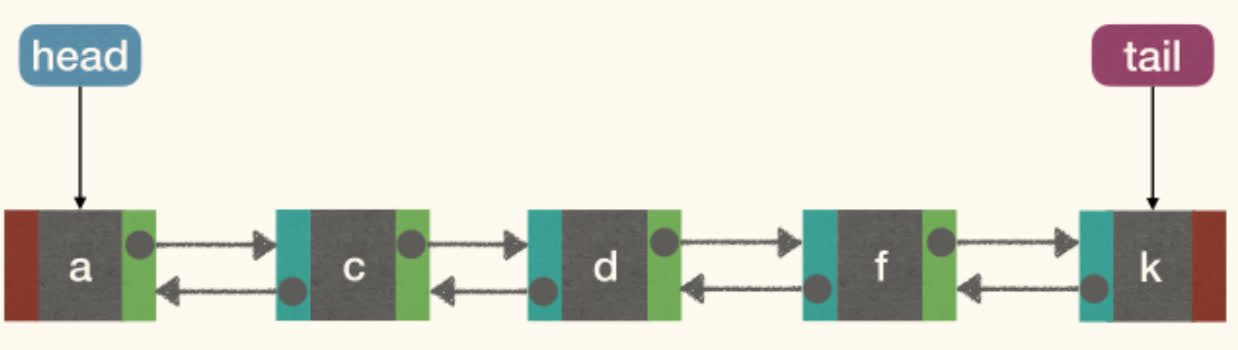
A circular, doubly linked list with a sentinel(哨兵) node:

• A sentinel node is a dummy node(虚拟节点) used as an alternative over using NULL as the path terminator
• The sentinel's next points to the first node on the list, and its prev points to the last node on the list.
• The first node's prev points to the sentinel, as does the last node's next.

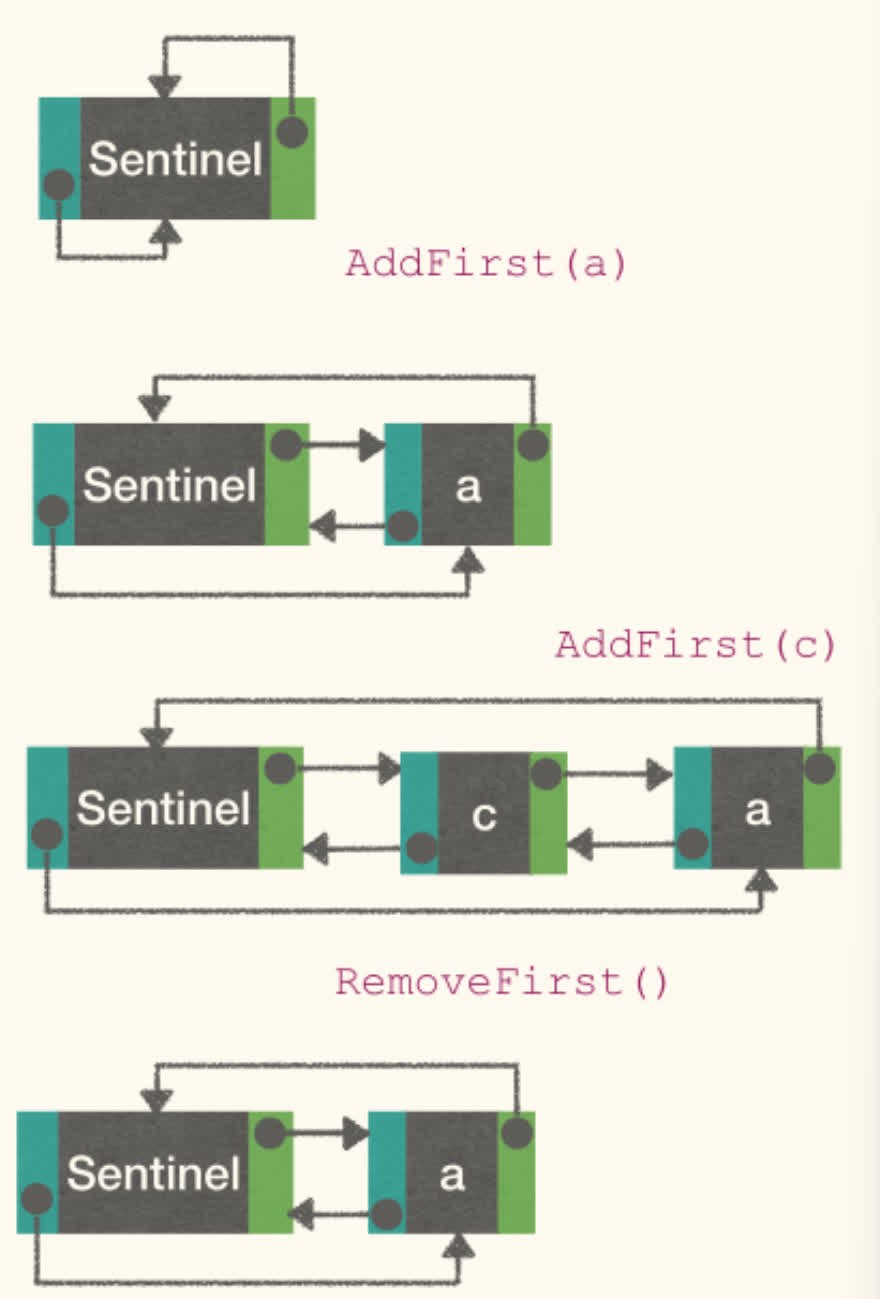
• AddFirst(x):

  x.next := sentinel.next
  sentinel.next.prev := x
  sentinel.next := x
  x.prev := sentinel

• RemoveFirst():

  sentinel.next := sentinel.next.next
  sentinel.next.prev := sentinel

In this way, we can avoid the boundary conditions. We no longer need to check if head is NULL, which fastens the operations (no branches).

Applications

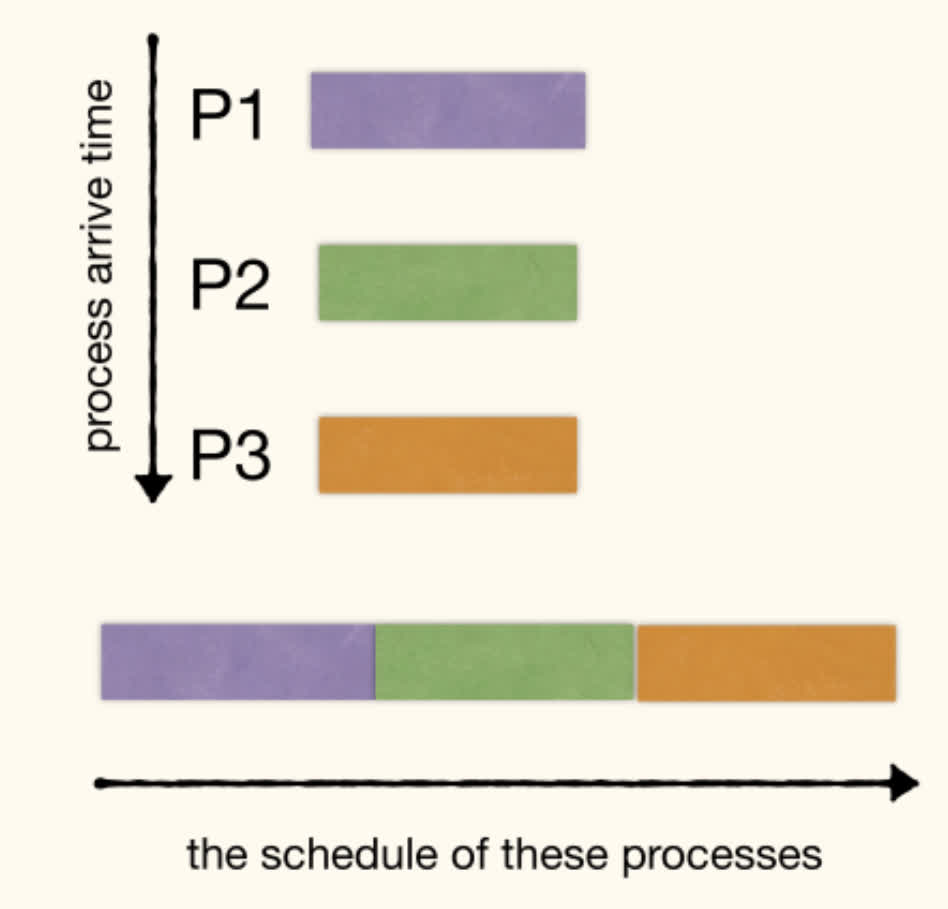
FIFO Queue

• Process Scheduling
  

Stack

• Balancing Symbols
• Function Calls
• Eliminating Recursion (with the help of a stack, recursion can be replaced by iteration)
  • Cons: Recursion can be slow and memory consuming due to the creation and maintenance of stack frames.
  • Pros: Recursion can make the code clearer, concise, and intuitive.

A function is called tail-recursive(尾递归) if each activation of the function will make at most one single recursive call, and will return immediately after that call.

• Recursion can be converted into iteration
  • Generic method: simulate a call stack
  • Special case: tail recursion
• Iteration can be converted into tail recursion
  • No one is always perfect
  • Iteration can be faster and more memory efficient
  • Recursion can be clearer, more concise and intuitive