并查集

DisjointSet ADT

DisjointSet

A DisjointSet(并查集) ADT (also known as Union-Find ADT) maintains a collections

$$\mathcal{S} = \left\lbrace S_1, S_2, \dots, S_k \right\rbrace$$

of sets that are disjoint and dynamic.

Each set $S_i$ is represented by a representative element (i.e., a leader)

The ADT supports the following operations:

• MakeSet(x): Create a set containing only x, add the set to S.
• Union(x, y): Find the sets containing x and y, say $S_x$ and $S_y$, remove $S_x$ and $S_y$ from S, and add $S_x \cup S_y$ to S.
• Find(x): Return a pointer to the leader of the set containing x.

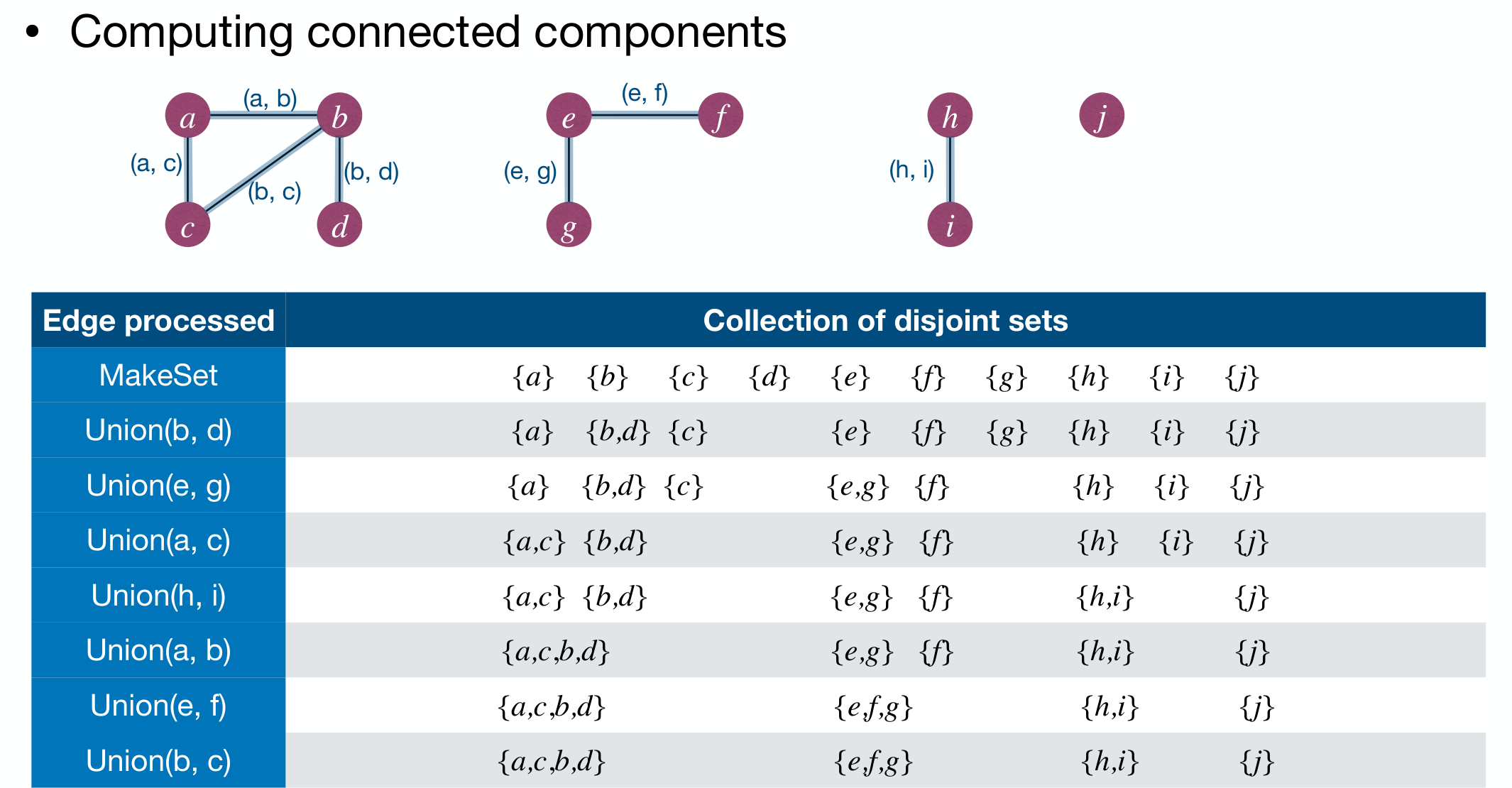
Sample application of DisjointSet ADT: Computing connected components.

Implementation

LinkedList

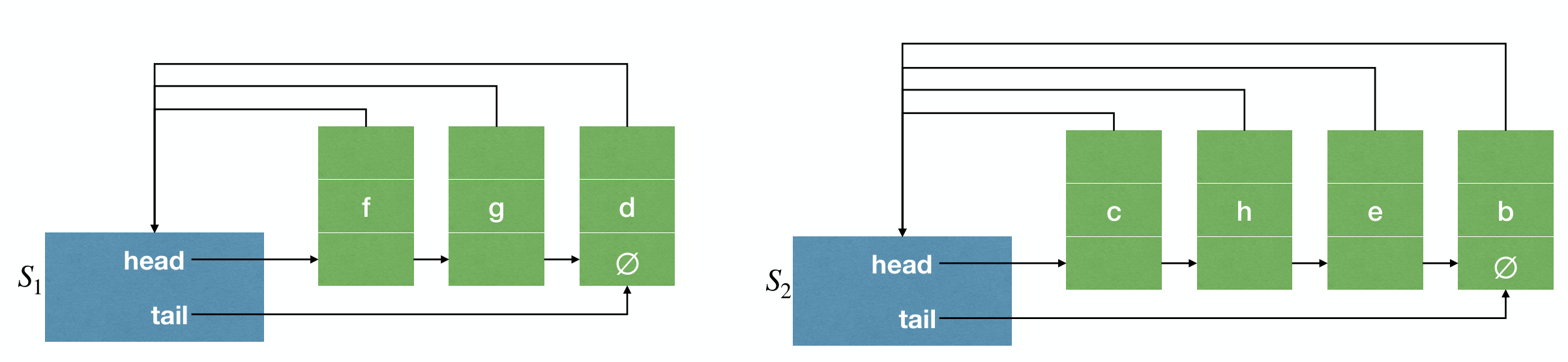
Basic Idea: Use a LinkedList to store and represent a set.

Details:

• A set object has pointers pointing to head and tail of the LinkedList.
• The LinkedList contains the elements in the set.
• Each element has a pointer pointing back to the set object.
• The leader of a set is the first element in the LinkedList.

Operations:

• MakeSet(x): Create a new set containing only x.
  • $\Theta(1)$
• Find(x): Follow pointer from x back to the set object, then return pointer to the first element in the LinkedList.
  • $\Theta(1)$
• Union(x, y):
  • Append list in $S_y$ to list in $S_x$, Destroy set object $S_y$
    • $\Theta(1)$
  • Update set object pointers for elements originally in $S_y$
    • Time depends on size of $S_y$

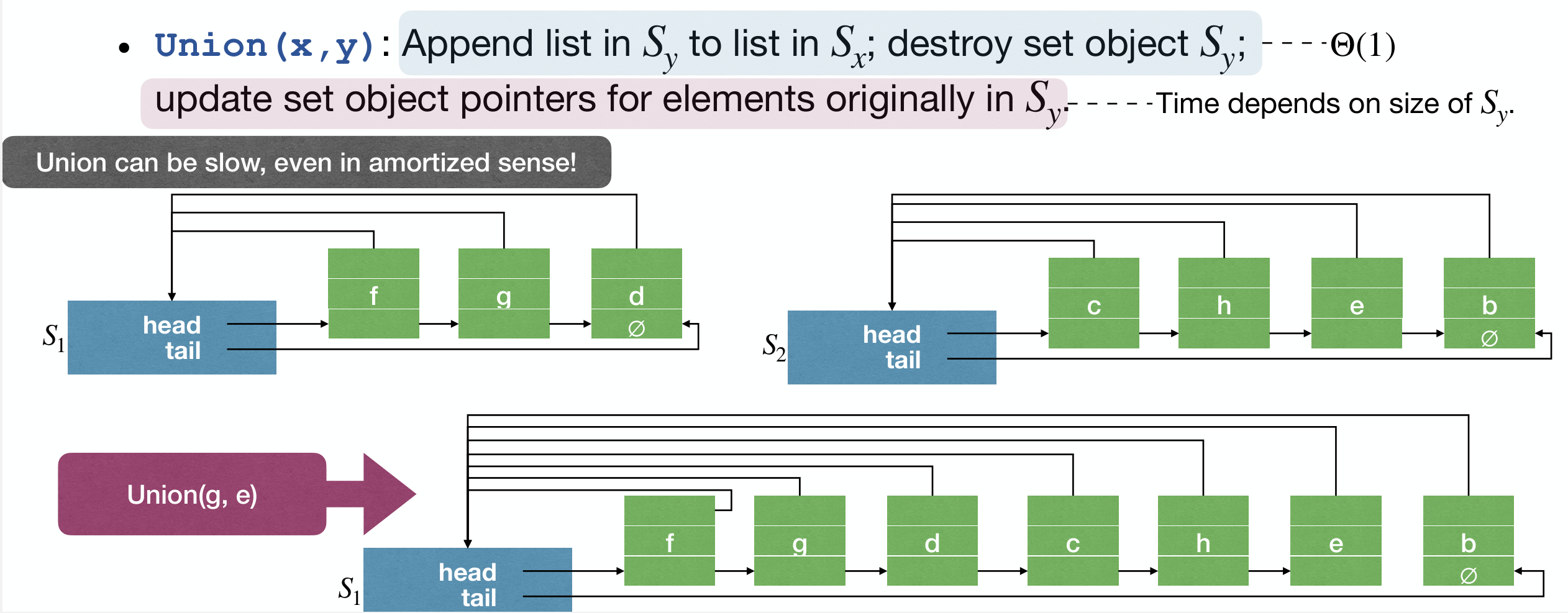
The worst case of Union(x, y):

$n$ 次 Union 操作的最差序列，这里计算的是 amortized cost。

MakeSet(x0)
for i := 1 to n
    MakeSet(xi)
    Union(xi, x0)

causing $1 + 2 + \dots + n = \Theta(n^2)$ time in total.

Each MakeSet takes $\Theta(1)$ time, but the average cost of Union reaches $\Theta(n)$.

• Improvement: Weighted-union heuristic (union-by-size)
• Basic Idea: In Union operation, always append the smaller list to the larger list.
• Complication: Need to maintain the size of each set.

However, in this case, the sequence above is no longer the worst case now.

Worst complexity of any sequence of $n+1$ MakeSet and then $n$ Union is $O(n \log n)$.

Proof Steps:

1. The $n+1$ MakeSet operation take $O(n)$ time in total.
2. For Union operation, cost dominated by set object pointer changes.
3. For each element, whenever its set object pointer changes, its set size at least doubles. (Improvement Definition)
4. Each element's set object pointer changes at most $\log n$ times.
5. Therefore the total cost of Union operations is $O(n \log n)$. ($n+1$ elements)

Average cost of Union operation is $O(\log n)$.

Rooted-tree

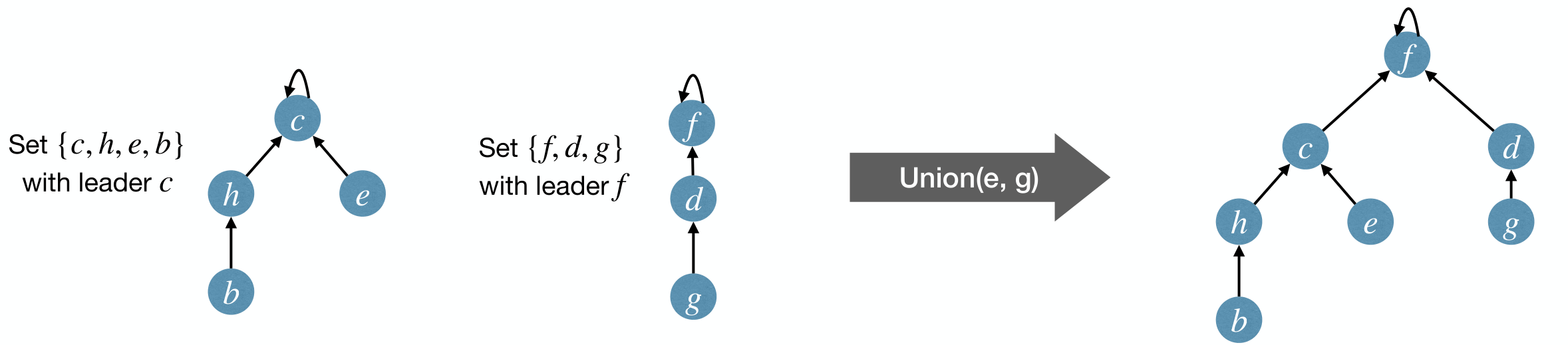
Basic Idea: Use a rooted tree to store and represent a set. The root of a tree is the leader of the set.

Details:

1. Each node has a pointer pointing to its parent. Parent of a leader is itself.

Operations:

• MakeSet(x): Create a new tree containing only x.
  • $\Theta(1)$
• Find(x): Follow parent pointer from $x$ back to the root, and return root.
• Union(x, y): Change the parent pointer of the root of $x$ to the root of $y$.

Time complexity of Find(x) and Union(x, y) depends on depth of $x$ and $y$.

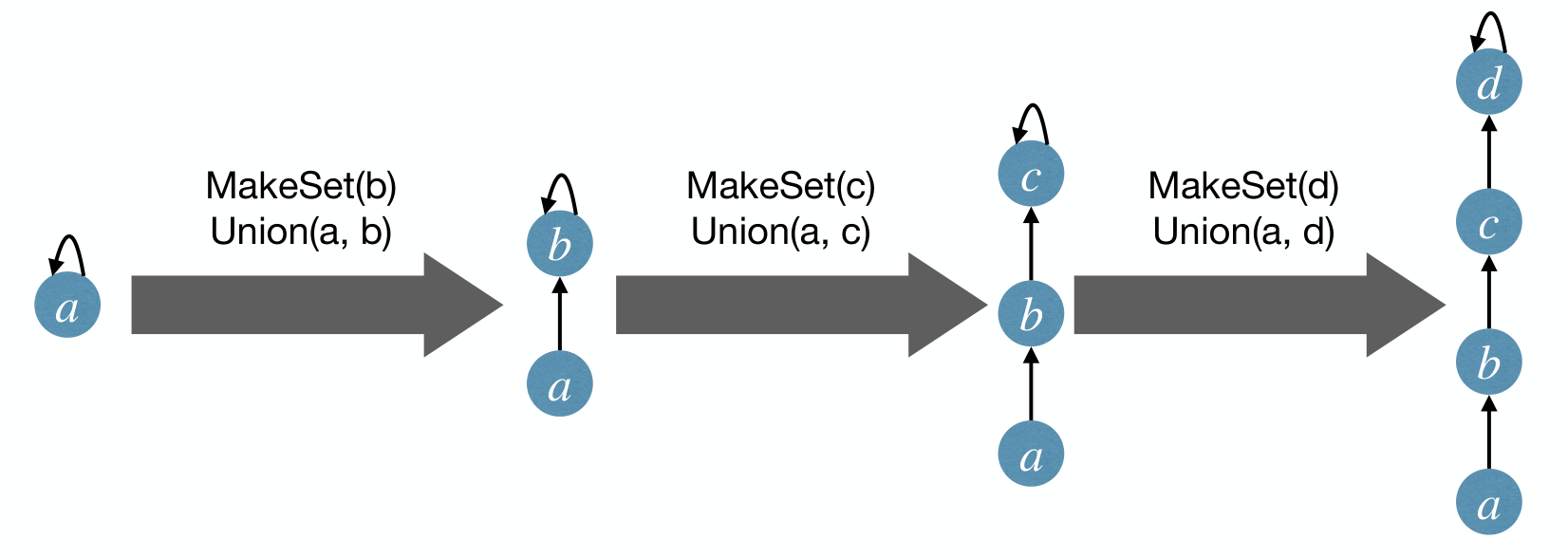
The worst case of Union(x, y): A sequence of $n$ Union can cost $\Theta(n)$ on average. And many following Find will also cost $\Theta(n)$.

• Improvement

1. Use union-by-size heuristic. Reduce worst-case cost of Union and Find to $O(\log n)$.
2. Use union-by-height heuristic. In Union, let tree of smaller height be subtree of larger height.

Path-compression in Find

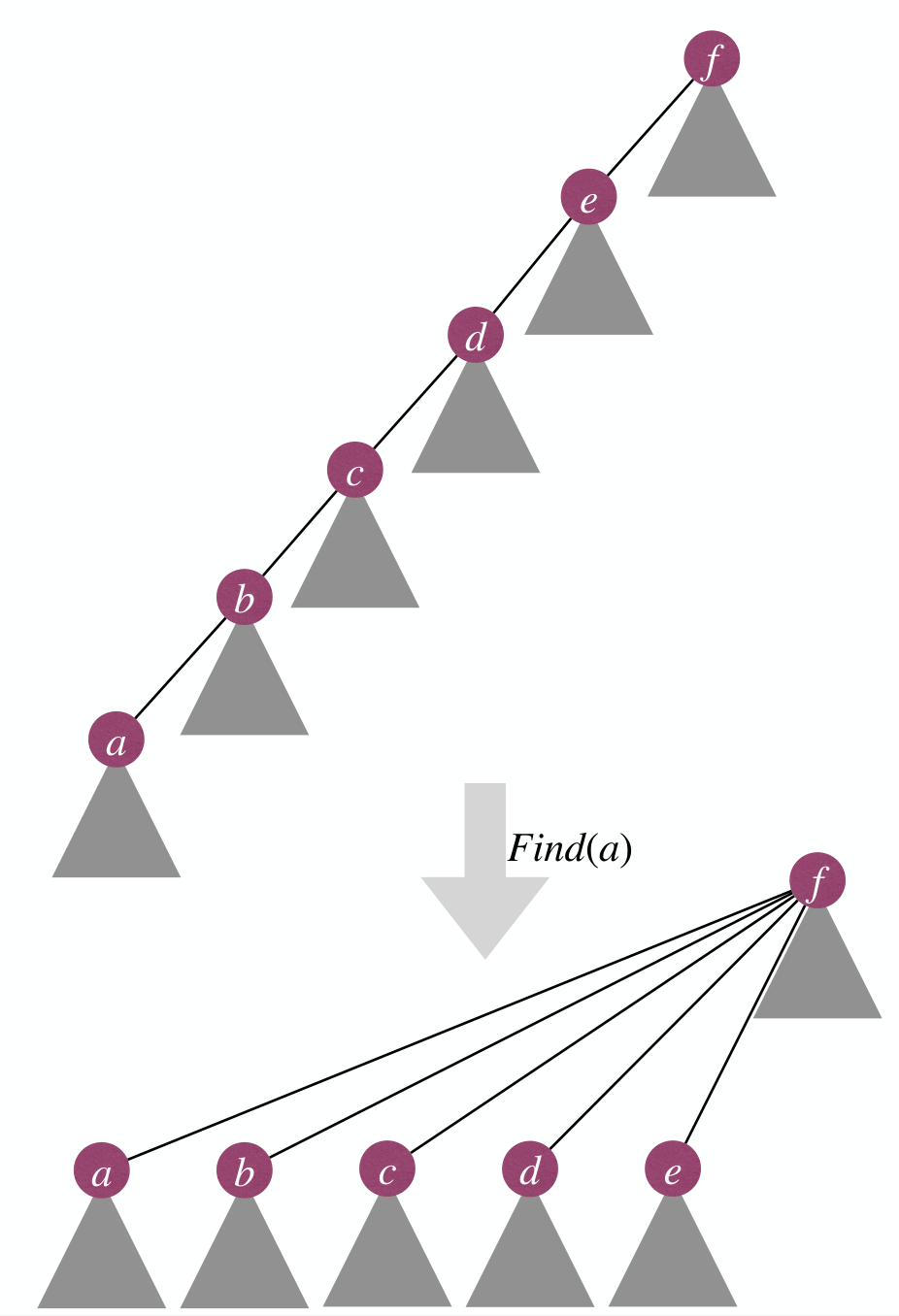
Do some work in Find to speed up future Find without increasing asymptotic cost of Find.

Path-Compression: In Find(x), when traveling from $x$ to root $r_x$, make all nodes on this path directly point to root $r_x$.

Path-compression will not increase cost of Find asymptotically.

Find can now change heights. Then maintaining heights becomes expensive.

• Solution: Ignore the impact on height when doing path compression. In such case, the height is referred to rank. The rank is always an upper bound of height.

The Find and Union operation of this implementation is almost $O(1)$.

Performance analysis for rooted-tree implementation with union-by-rank and path-compression*

Slowly Growing Functions

Consider the recurrence

$$C(N) = \begin{cases} 0, & \text{if } N \le 1 \\ C(\left\lfloor f(N) \right\rfloor) + 1, & \text{if } N > 1 \end{cases}$$

In this equation, $C(N)$ represents the number of times, starting at $N$ that we must iteratively apply $f(N)$ until we reach $1$ or less.

We assume that $f(N)$ is a nicely defined function that reduces $N$. Call the solution to the equation $f^{*}(N)$.

• When $f(N) = N - 2$, $f^{*}(N) = \dfrac{N}{2}$.
• When $f(N) = \dfrac{N}{2}$, $f^{*}(N) = \log N$.
• When $f(N) = \log N$, $f^{*}(N) = \log^{*} N$, which grows extremely slow.

Performance Analysis*

懒得记了，看 PPT 得了。