图及其遍历

本节可以参考《离散数学》笔记「图论初步」。

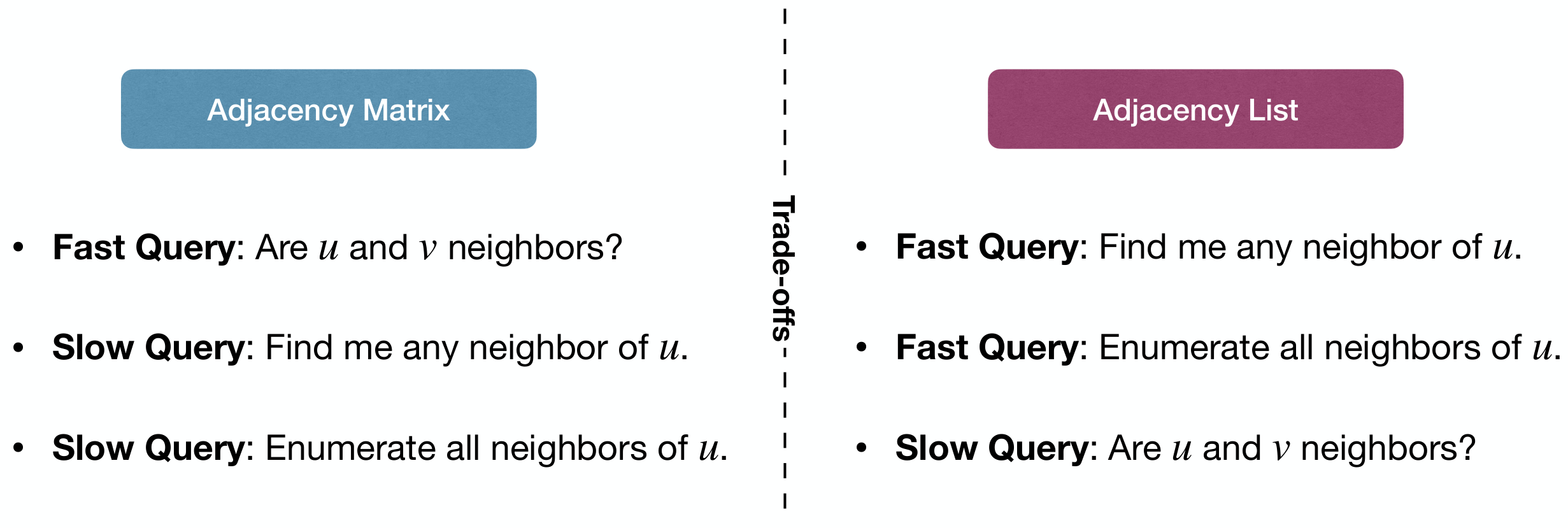
Representations

一些定义直接复制《离散数学》笔记了。

$|V| = n$ and $|E| = m$.

邻接矩阵（Adjacency Matrix）

简单有向图 $G = (V, E, \varphi)$，不妨设 $V = \left\lbrace v_1, \cdots, v_n \right\rbrace,\, E = \left\lbrace e_1, \cdots, e_m \right\rbrace$。

则 $A(G) = [a_{ij}]$ 称为 $G$ 的邻接矩阵（$n \times n$ 阶矩阵），其中

$$a_{ij} = \begin{cases} 1, & \text{若 } v_i \text{ 邻接到 } v_j \\ 0, & \text{否则} \end{cases}$$

$v_i, v_{j}$ 相邻即存在 $e \in E$ 使得 $\varphi(e) = (v_i, v_j)$。

Space cost $\Theta(n^2)$ memory regardless of $m$.

邻接表（Adjacency List）

邻接表：对于每个顶点 $v_i$，记录与之相邻的顶点。（有向图无向图均可用）

邻接矩阵中元素为 $0, 1$，称为布尔矩阵。若表示包含多重边的图，则不是布尔矩阵。

Space cost $\Theta(m + n)$.

Comparison:

Graph Traversal (Searching in a Graph)

Use adjacency list below.

Goal:

• Start at source node $s$ and find some node $t$.
• Or visit all nodes reachable from $s$.

Strategies:

• Breadth-first search (BFS, 广度优先搜索)
• Depth-first search (DFS, 深度优先搜索)

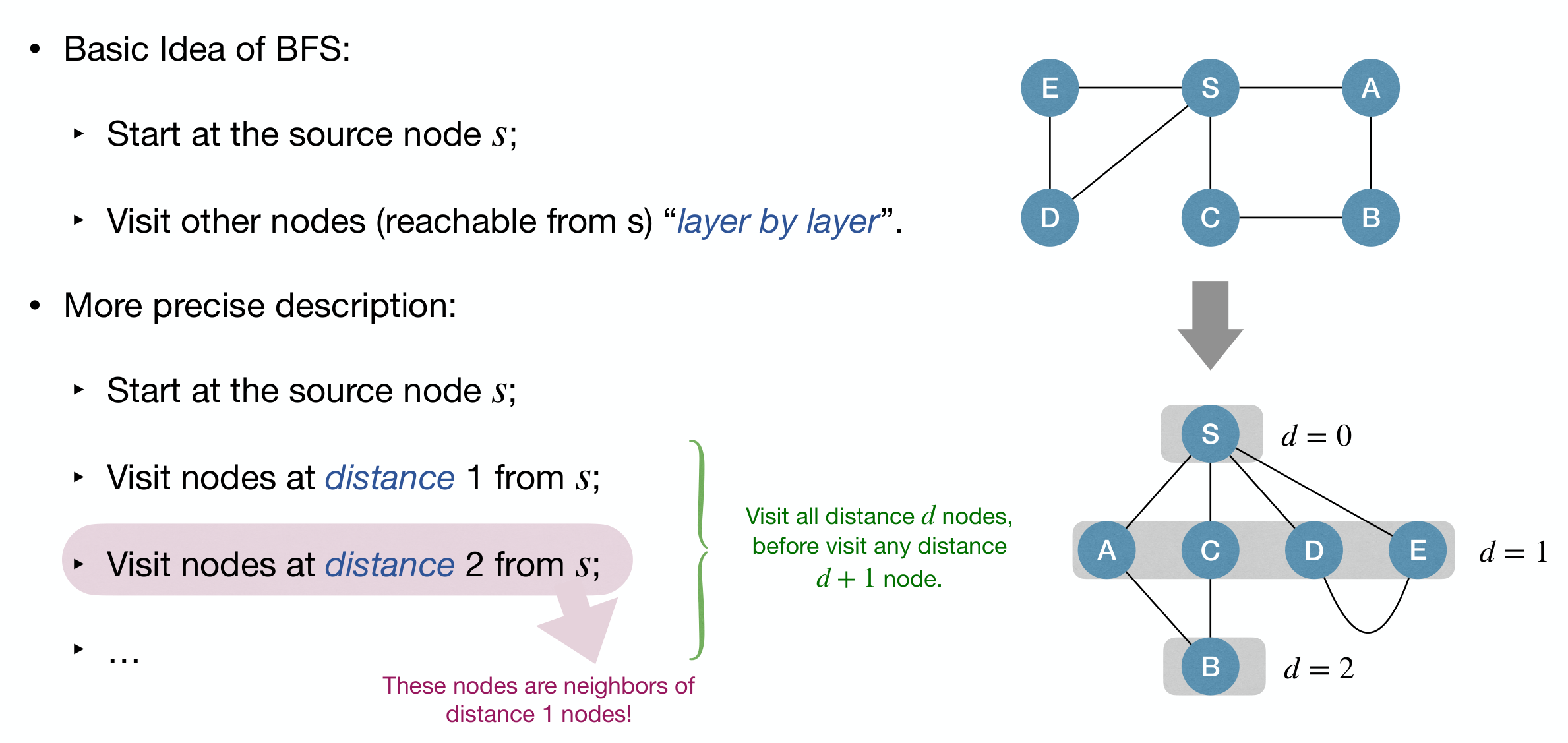
Breadth-First Search (BFS)

Basic idea:

• Start at the source node $s$;
• Visit other nodes layer by layer.

Implementation:

BFSSkeleton(G, s):
for each u in V
    u.dist := INF
    u.discovered := False
s.dist := 0
s.discovered := True
Q.enqueue(s)
while !Q.isEmpty()
    u := Q.dequeue()
    for each edge(u, v) in E
        if !v.discovered
            v.dist := u.dist + 1
            v.discovered := True
            Q.enqueue(v)

Nodes have 3 status:

• Undiscovered: Not in queue yes;
• Discovered but not visited: In queue but not processed;
• Visited: Ejected from queue and processed.

Use Color instead, WHITE, GRAY, BLACK.

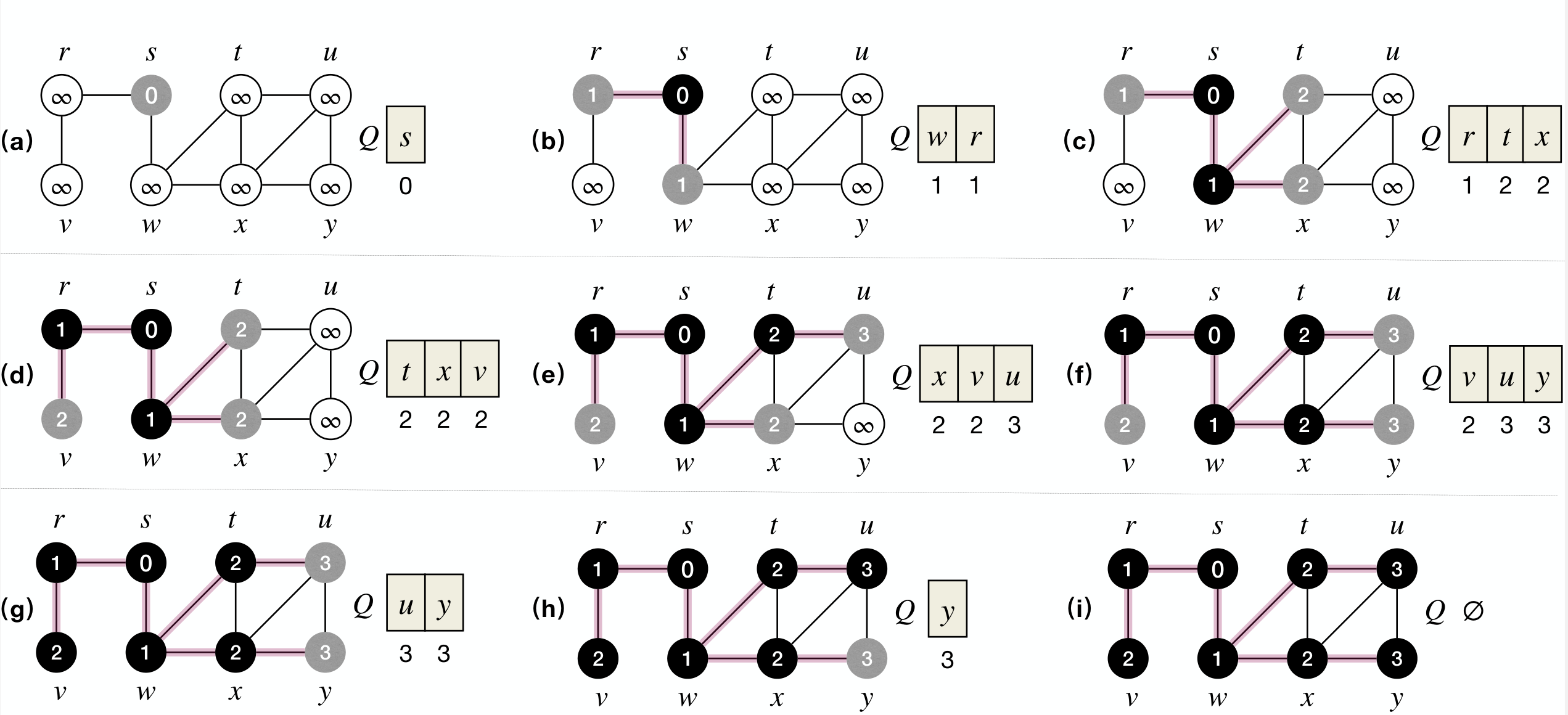
BFD(G, s):
for each u in V
    u.c := WHITE
    u.d := INF
    u.p := NIL
s.c = GRAY
s.d = 0
s.p = NIL
Q.enqueue(s)
while !Q.isEmpty()
    u := Q.dequeue()
    u.c = BLACK
    for each edge(u, v) in E
        if v.c = WHITE
            v.c = GRAY
            v.d = u.d + 1
            v.p = u
            Q.enqueue(v)

The improved version also records the shortest path, instead of just the distance.

Process:

Performance:

• while loop costs $\Theta(2)$ times since each node in $Q$ at most once.
• for loop costs $\Theta(m)$ times since each edge visited at most once or twice.
• Total cost: $\Theta(n + m)$.

Some theorems without proof (cos I'm lazy):

BFS visits a node iff it is reachable from the source node.

BFS correctly computes u.dist for every node $u$ reachable from the source node.

Corollay: For any $u \ne s$ that is reachable from $s$, one of the shortest path from $s$ to $u$ is a shortest path from $s$ to $u$'s parent followed by the edge between $u$'s parent and $u$.

$G_p = (V_p, E_p)$ is a breadth-first tree, which can print on a shortest path from any node $v$ to the source node $s$.

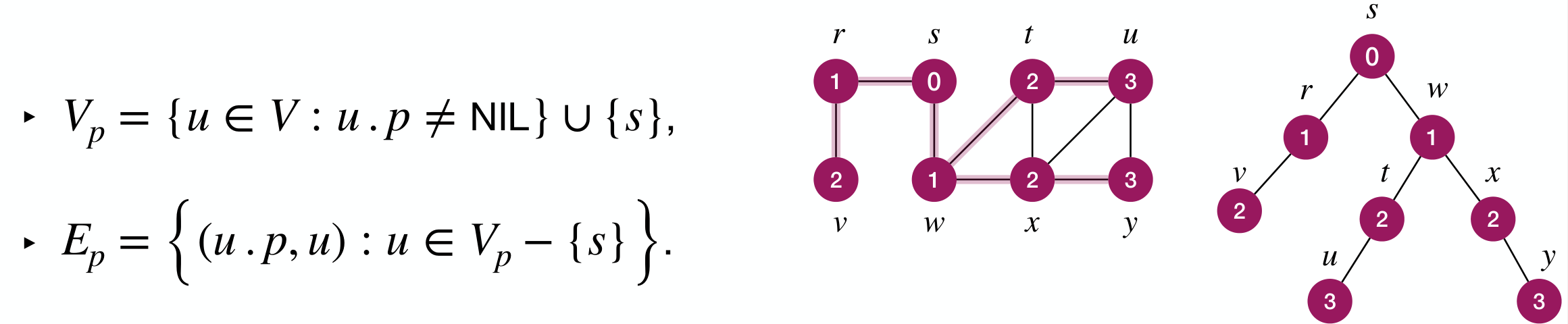
What if graph is not connected? Do a BFS for each connected component.

BFD(G, s):
for each u in V
    u.c := WHITE
    u.d := INF
    u.p := NIL
for each u in V
    if u.c = WHITE
        u.c = GRAY
        u.d = 0
        u.p = NIL
        Q.enqueue(u)
        while !Q.isEmpty()
            v := Q.dequeue()
            v.c = BLACK
            for each edge(v, w) in E
                if w.c = WHITE
                    w.c = GRAY
                    w.d = v.d + 1
                    w.p = v
                    Q.enqueue(w)

Depth-First Search (DFS)

Like exploring a maze:

1. Use a ball of string and a piece of chalk.
   • Chalk: Boolean variables.
   • String: A stack.
2. Follow path (unwind string and mark at intersections), until stuck (reach dead-end or already-visited place).
3. Backtrack (rewind string), until find unexplored neighbor (intersection with unexplored direction).
4. Repeat above two steps.

DFSSkeleton(G, s):
s.visited := True
for each edge(s, v) in E
    if !v.visited
        DFSSkeleton(G, v)

DFSIterSkeleton(G, s):
Stack Q
Q.push(s)
while !Q.isEmpty()
    u := Q.pop()
    u.visited := True
    for each edge(u, v) in E
        if !v.visited
            Q.push(v)
// This code is a little different from PPT.
// `Q` here only contains node unvisited while 
// `Q` in PPT contains all sub nodes.

Process:

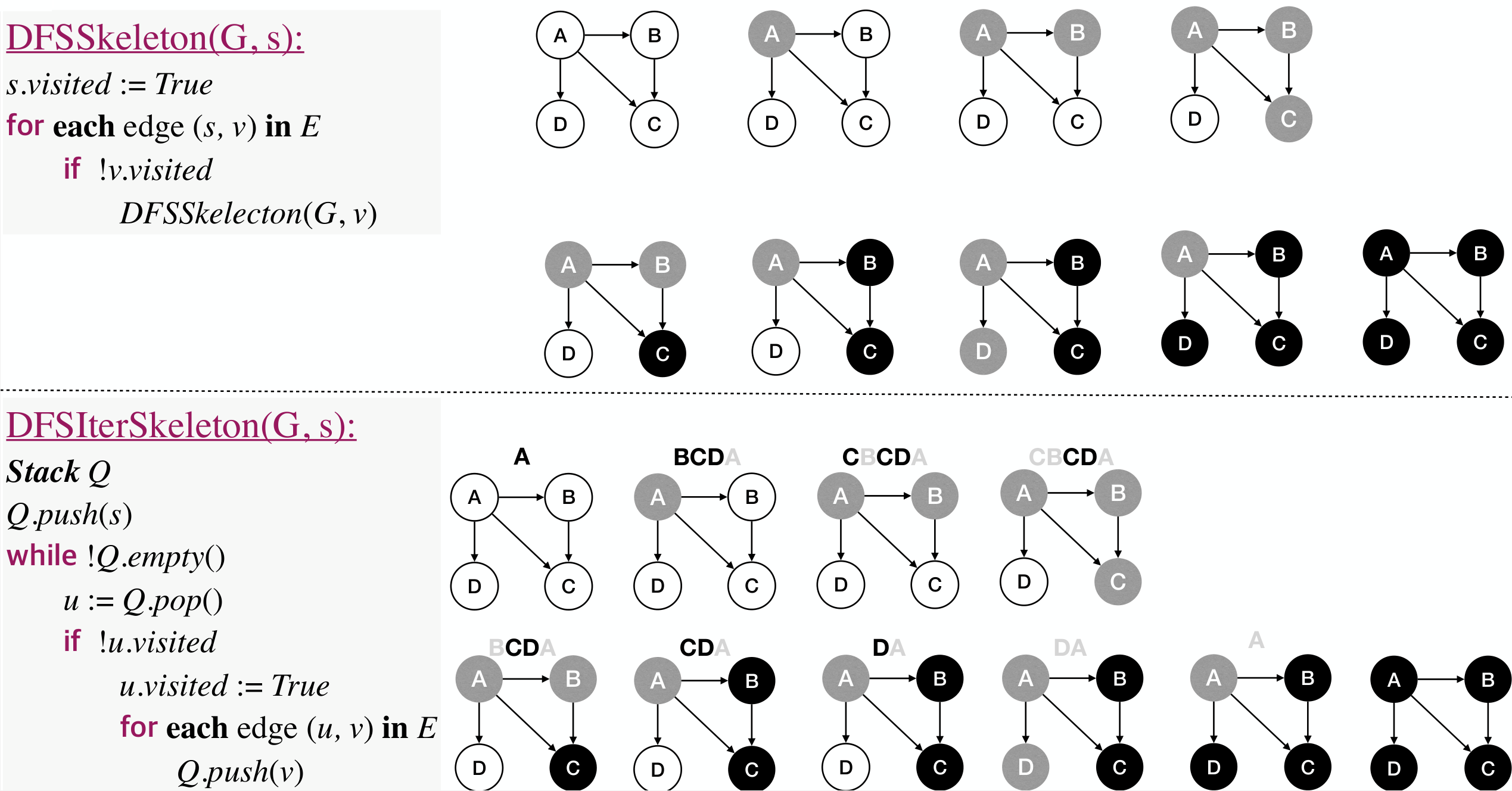
Do DFS from multiple sources if the graph is not (strongly) connected.

DFSAll(G):
for each u in V
    u.visited := False
for each u in V
    if !u.visited
        DFSSkeleton(G, u)

Each node $u$ have 3 status during DFS:

• Undiscovered WHITE: before calling DFSSkeleton(G, u);
• Discovered GRAY: during execution of DFSSkeleton(G, u);
• Finished BLACK: DFSSkeleton(G, u) returned.

DFS(G, u) builds a tree among nodes reachable from $u$:

• Root of this tree is $u$;
• For each non-root, its parent is the node that makes it turns GRAY.

DFS on entire graph builds a forest.

DFSAll(G):
for each node u in V
    u.c := WHITE
    u.p := NIL
for each node u in V
    if u.c = WHITE
        DFS(G, u)

DFS(G, s):
s.c := GRAY
for each edge(s, v) in E
    if v.c = WHITE
        v.p := s
        DFS(G, v)
s.c := BLACK

Process:

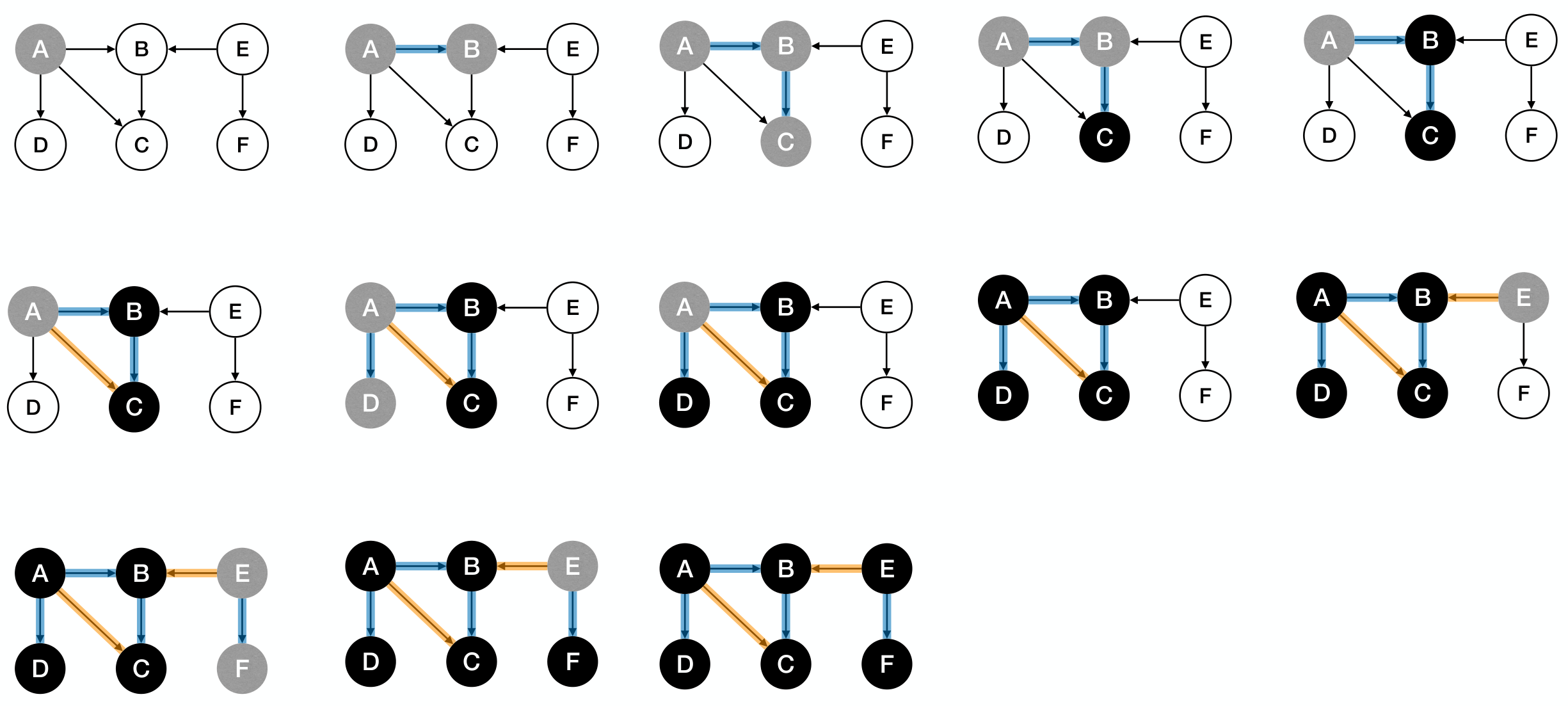
DFS provides (at least) two chances to process each node:

• Pre-visit: WHITE to GRAY
• Post-visit: GRAY to BLACK

DFSAll(G):
PreProcess(G)
...

DFS(G, s):
PreVisit(s)
...
PostVisit(s)

Some application: Track active intervals of nodes

• Clock ticks whenever some nodes's color changes.
• Discovery time: when the node turns to GRAY.
• Finish time: when the node turns to BLACK.

PreProcess(G):
time := 0

PreVisit(s):
time := time + 1
s.d := time // indicates the discovery time

PostVisit(s):
time := time + 1
s.f := time // indicates the finish time

Example:

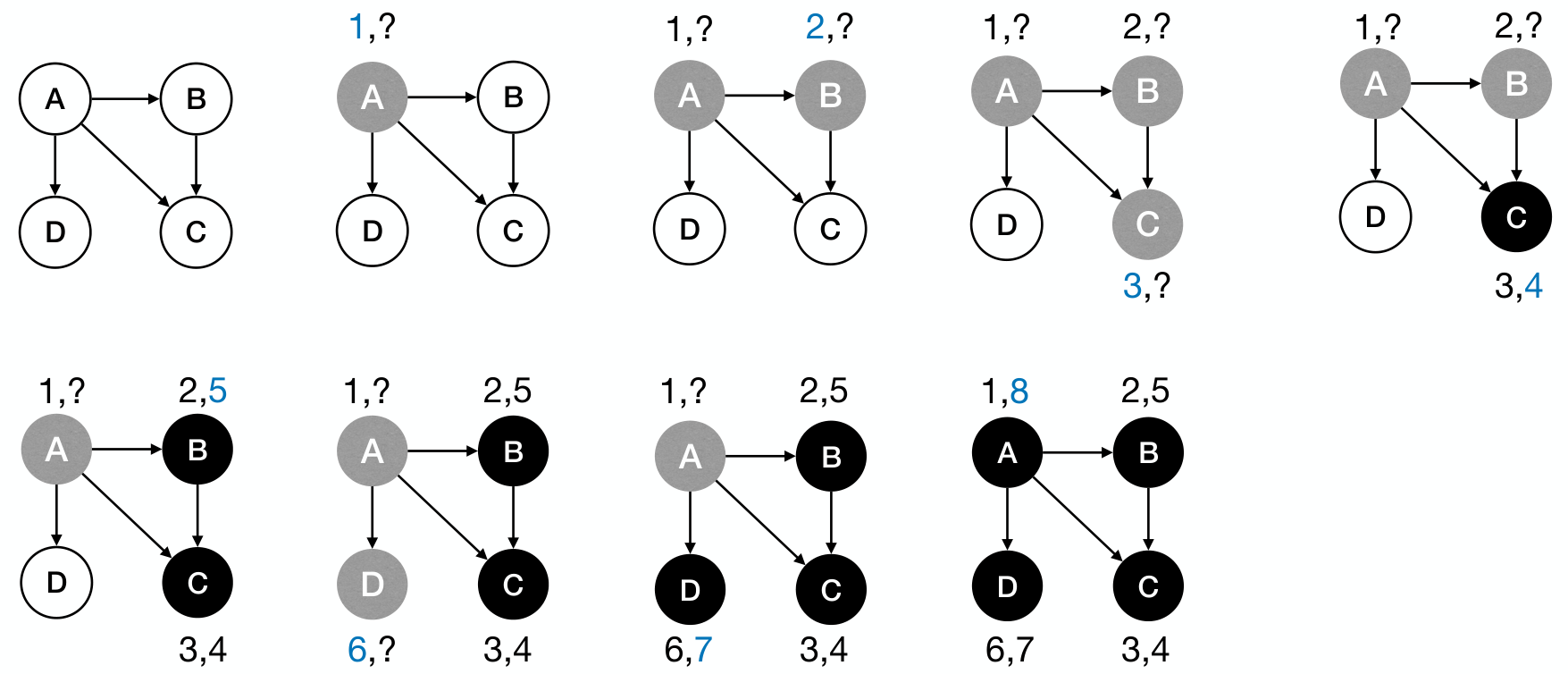
Performance:

• Time spent on each node is $O(1)$ and DFS(G, u) is called once for each node $u$.
• Time spent on each edge is $O(1)$ and each edge is examined $O(1)$ time.
• Total cost: $\Theta(n + m)$.

DFS process classify edges of input graph into 4 types:

• Tree Edges: Edges in DFS forest.
• Back Edges: Edges $(u, v)$ connecting $u$ to an ancestor $v$ in a DFS tree.
• Forward Edges: Non-tree edges $(u, v)$ connecting $u$ to a descendant $v$ in a DFS tree.
• Cross Edges: Other edges.
  • Connecting nodes in same DFS tree with no ancestor-descendant relation, or connecting nodes in different DFS trees.

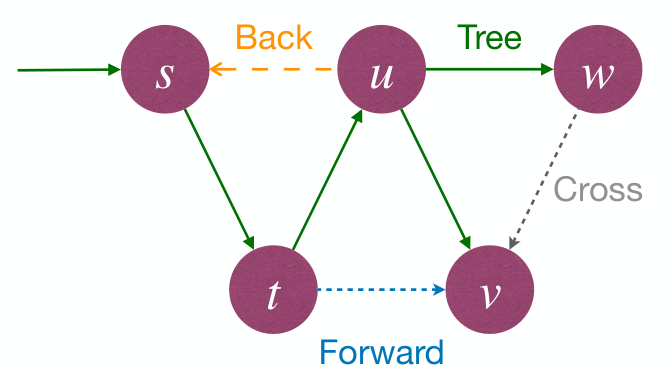
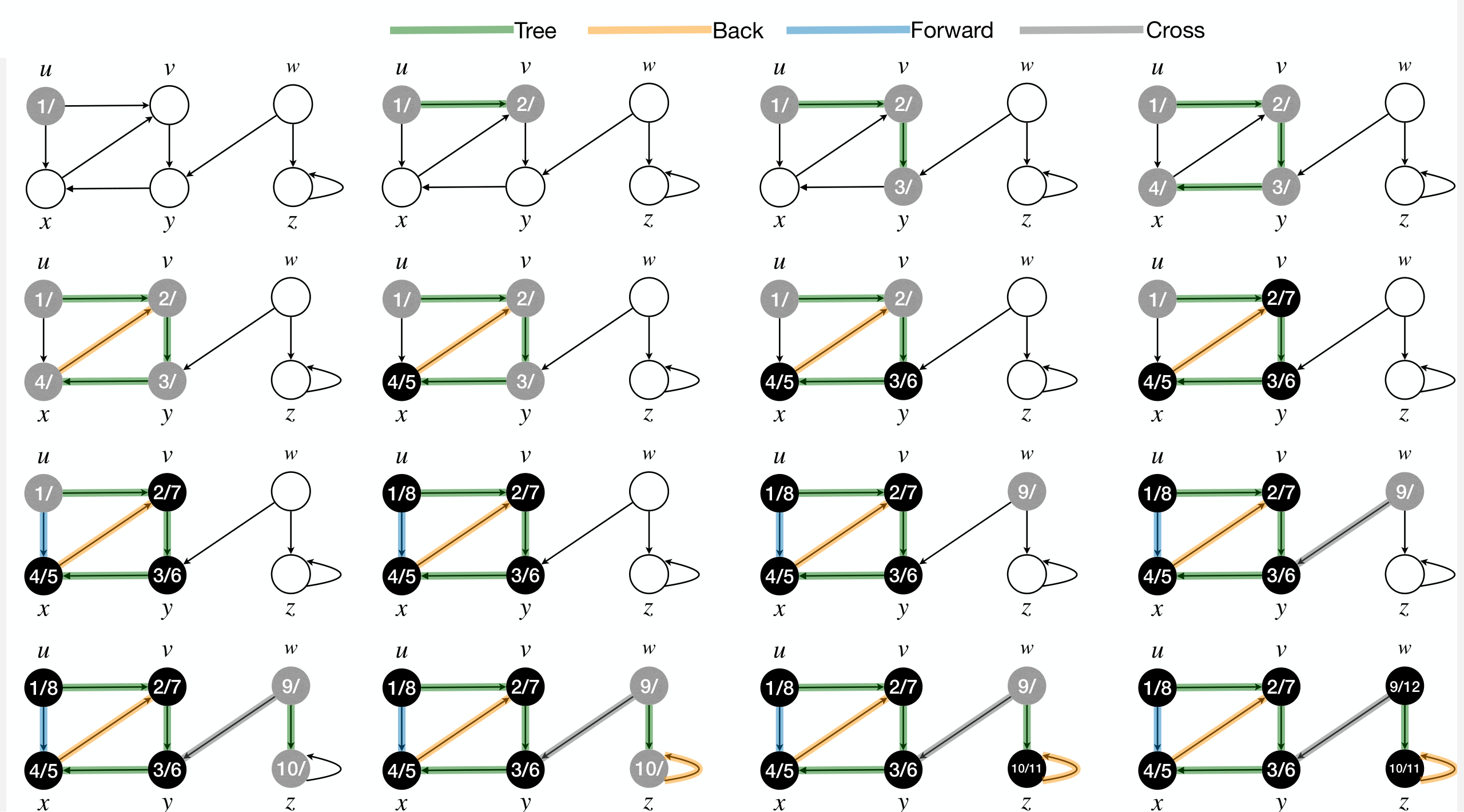
Properties

Parenthesis Theorem

Active intervals of two nodes are either:

1. entirely disjoint
2. one is entirely contained within another

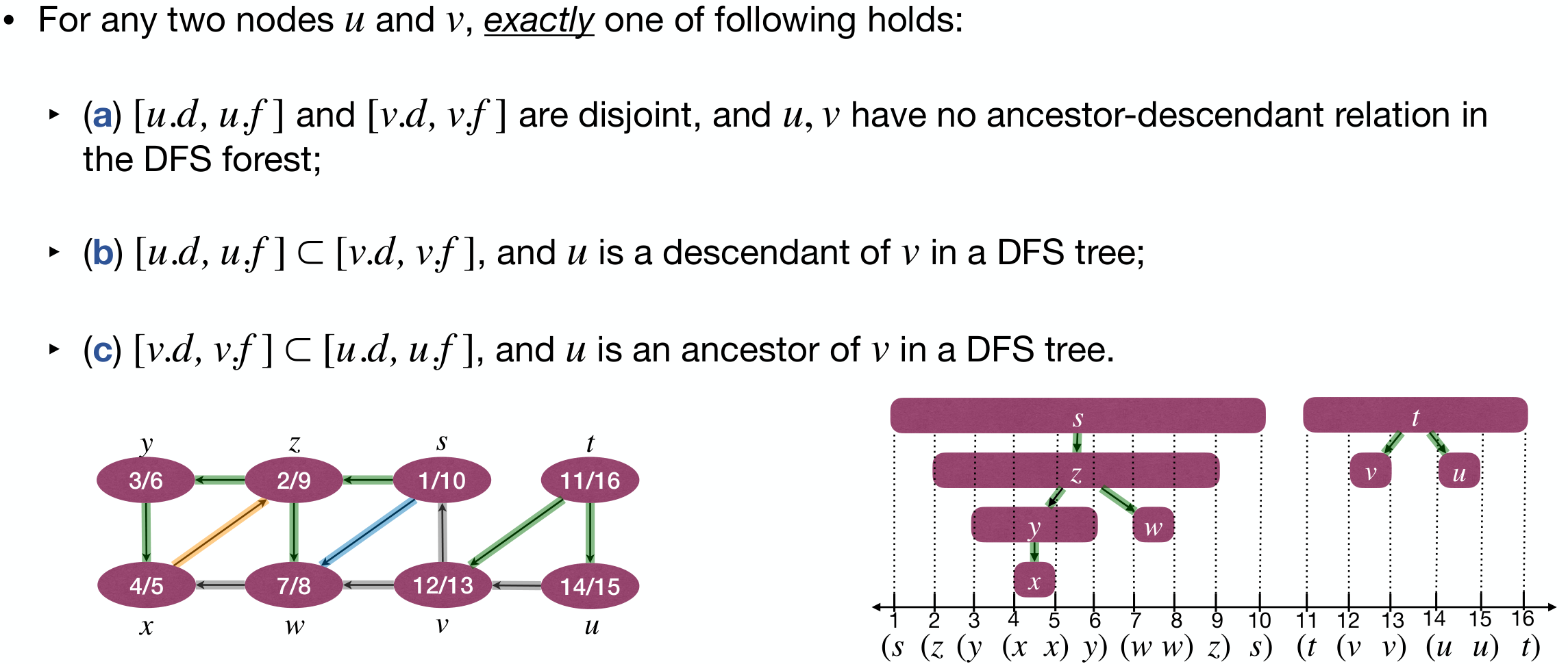
Proof.

W.l.o.g., assume $u.d < v.d$.

• If $v.d < u.f$: then $v$ is discovered (WHITE to GRAY) while $u$ is being processed (GRAY); and DFS will finish $v$ first before returning to $u$.
  • In this case, $[v.d, v.f] \subset [u.d, u.f]$ and $u$ is an ancestor of $v$.
• If $v.d > u.f$: then obviously $u.d < u.f < v.d < v.f$; and DFS has finished exploring $u$ (BLACK), before $v$ is discovered (WHITE to GRAY).
  • In this case, $[u.d, u.f]$ and $[v.d, v.f]$ are disjoint, and $u, v$ have no ancestor-descendant relation.

White-path Theorem

In the DFS forest, $v$ is a descendant of $u$ iff when $u$ is discovered, and there is a path in the graph from $u$ to $v$ containing only WHITE nodes.

Proof.

$\implies$:

Claim: If $v$ is a proper descendant of $u$, then $v$ is WHITE when $u$ is discovered. Since if $v$ is a proper descendant of $u$, then $u.d < v.d$.

For any node along the path from $u$ to $v$ in the DFS forest, above claim holds.

Therefore $\implies$ direction of the theorem holds.

$\impliedby$:

W.l.o.g., assume $v$ is the first node along the path that does not become a descendant of $u$. So we get $[v_{k}.d, v_{k}.f] \subset [u.d, u.f]$.

But $v$ is discovered after $u$ is discovered and must before $v_{k}$ is finished. So we have $u.d < v.d < v_{k}.f \le u.f$.

Then it must be $[v.d, v.f] \subset [u.d, u.f]$, implying $v$ is a descendant of $u$.

Classification of edges

Determine edge $(u, v)$ type by color of $v$ during DFS execution:

• Tree Edges: Node $v$ is WHITE.
• Back Edges: Node $v$ is GRAY.
• Forward Edges: Node $v$ is BLACK
• Cross Edges: Node $v$ is BLACK

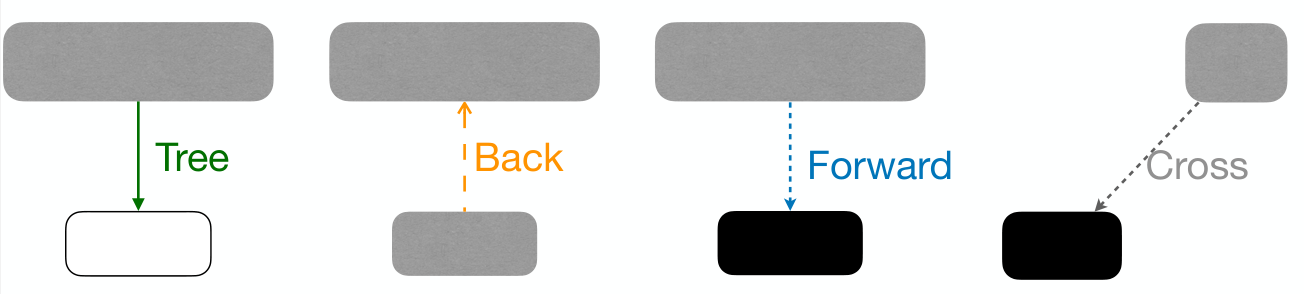
Types of edges in undirected graphs

In DFS of an undirected graph $G$, every edge of $G$ is either a Tree Edge or a Back Edge.

Proof

Consider an arbitrary edge $(u, v)$. W.l.o.g., assume $u.d < v.d$.

Edge $(u, v)$ must be explored while $u$ is GRAY.

Consider the first time the edge $(u, v)$ is explored:

• If the direction is $u \to v$: Then $v$ must be WHITE by then, for otherwise the edge would have been explored from direction $v \to u$ earlier.
• If the direction is $v \to u$: Then the edge is GRAY to GRAY, which is a Back Edge.

Other queuing disciplines lead to other search.

Applications of DFS

Directed Acyclic Graphs (DAGs)

A graph without cycles is called acyclic(无环).

A directed graph without cycles is a directed acyclic graph (DAG, 有向无环图).

DAGs are good for modeling relations such as: causalities, hierarchies, and temporal dependencies.

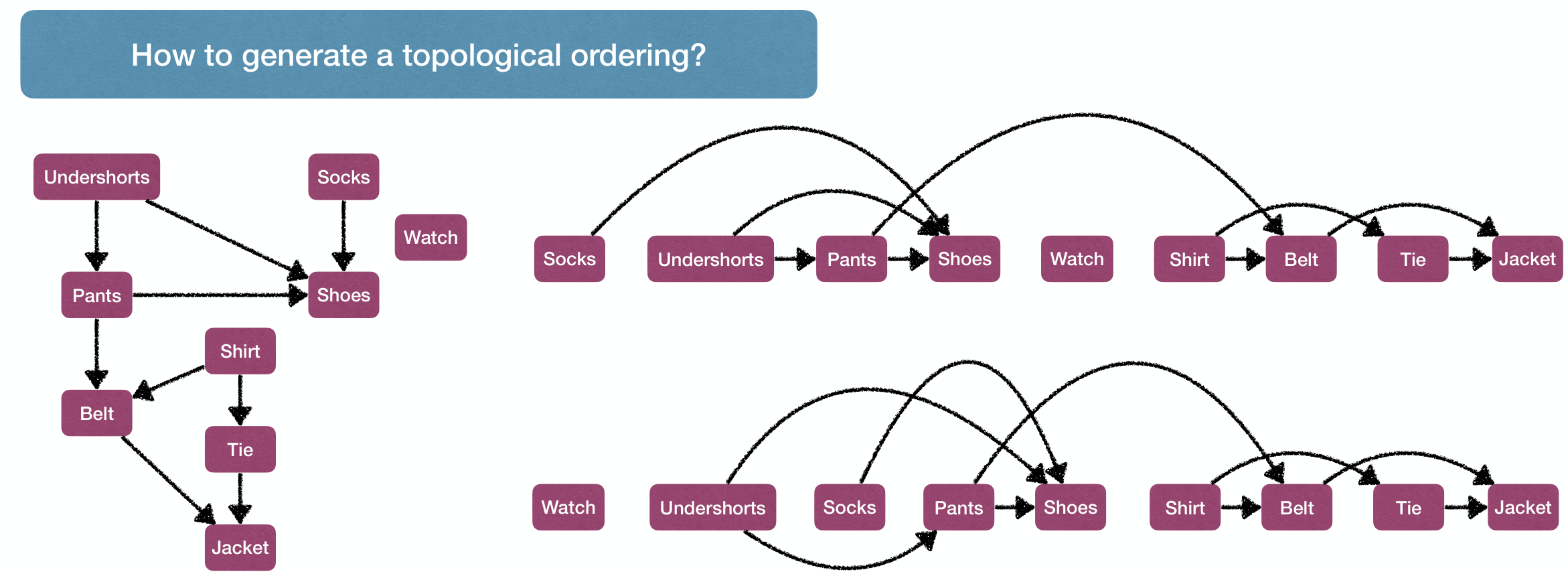
Topological Sort

A topological sort(拓扑序) of a DAG $G$ is a linear ordering of its vertices such that if $G$ contain an edge $(u, v)$, then $u$ appears before $v$ in the ordering.

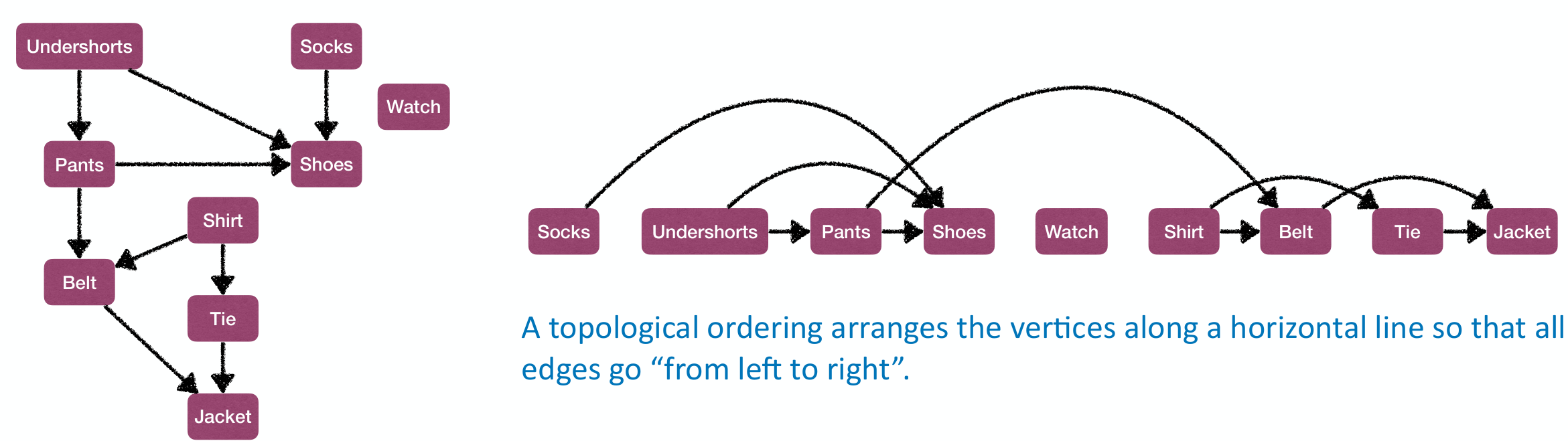
$E(G)$ defines a partial order over $V(G)$, a topological sort gives a total order over $V(G)$ satisfying $E(G)$.

Topological sort is impossible if the graph contains a cycle.

A given graph may have multiple different valid topological ordering.

Questions:

1. Does every DAG has a topological ordering?
2. If true, How to tell if a directed graph is acyclic?
3. If true, how to do a topological sort on a DAG?

Lemma 1

Directed graph $G$ is acyclic iff a DFS of $G$ yields no back edges.

Proof.

$\implies$:

For the sake of contradiction, assume DFS yields back edge $(u, v)$.

So $v$ is ancestor of $u$ in DFS forest, meaning there's a path from $v$ to $u$ in $G$.

But together with edge $(u, v)$ this creates a cycle. Contradiction!

$\impliedby$:

For the sake of contradiction, assume $G$ contains a cycle $C$.

Let $v$ be the first node to be discovered in C.

By the White-path theorem, $u$ is a descendant of $v$ in DFS forest.

But then when processing $u$, $(u, v)$ becomes a back edge!

Lemma 2

If we do a DFS in DAG $G$, then $u.f > v.f$ for every edge $(u, v)$ in $G$.

Proof.

When exploring $(u, v)$, $v$ cannot be GRAY, otherwise we have a back edge.

If $v$ is WHITE, then $v$ becomes a descendant of $u$ and $u.f > v.f$.

If $v$ is BLACK, then $u.f > v.f$.

As a result, decreasing order of finish times of DFS on DAG gives a topological ordering. Therefore, every DAG has a topological ordering.

Topological Sort of $G$:

1. Do DFS on $G$ and compute finish times for each node along the way;
2. When a node finishes, insert it to the head of a list;
3. If no back edge is found, then the list eventually gives a Topological Ordering.

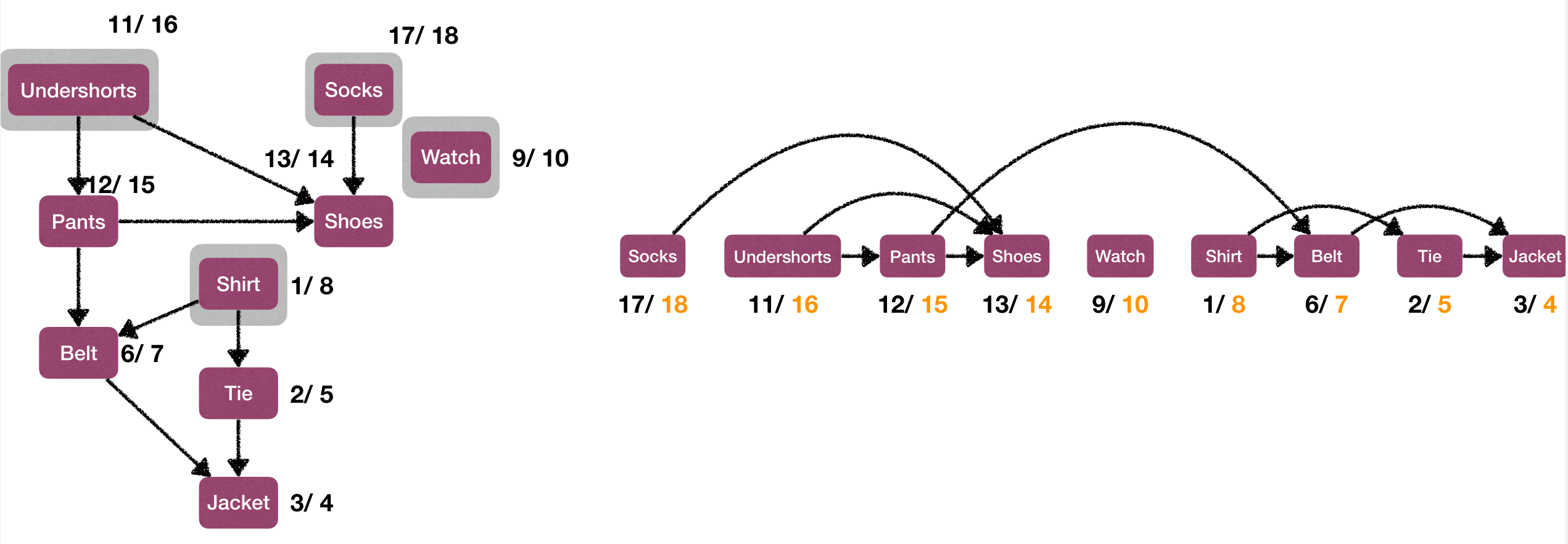
Time complexity is $\Theta(n + m)$.

Alternative Algorithm for Topological Sort

A source node(源头点) is a node with no incoming edges.

A sink node(汇点) is a node without outgoing edges.

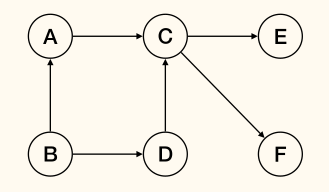
$B$ is source and $E, F$ are sink.

Obviously, each DAG has at least one source and one link.

Here are two observations:

1. In DFS of a DAG, node with max finish time must be a source.
   • Node with max finish time appears first in topological sort, it cannot have incoming edges.
2. In DFS of a DAG, node with min finish time must be a sink.
   • Node with min finish time appears last in topological sort, it cannot have outgoing edges.

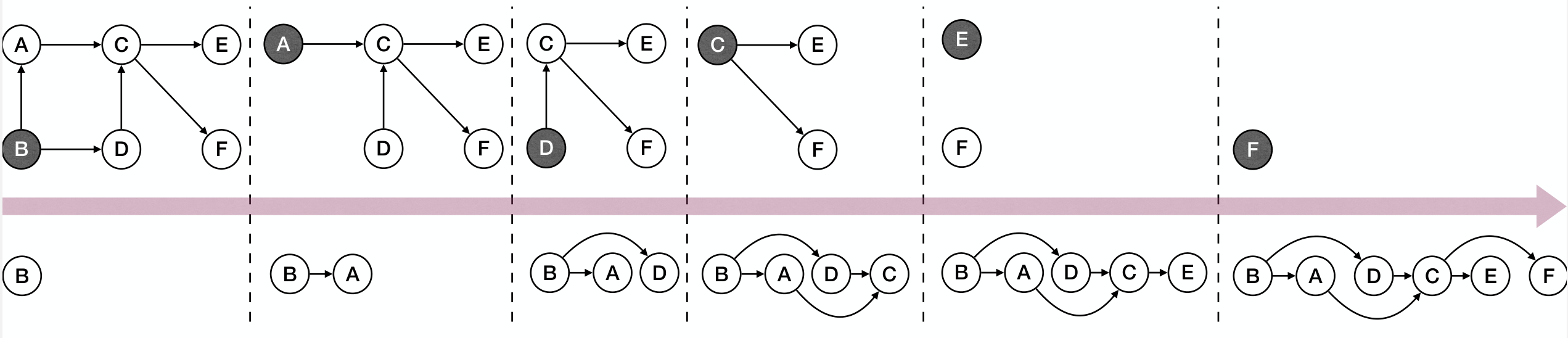
Alternative Algorithm for Topological Sort:

1. Find a source node $s$ in the (remaining) graph and output it;
2. Delete $s$ and all its outgoing edges from the graph;
3. Repeat until the graph is empty.

(Strongly) Connected Components

可部分参考《离散数学》笔记关于「连通分支」的内容。

Connected Components

For an undirected graph $G$, a connected component (CC, 连通分量) is a maximal set $C \subseteq V(G)$, such that for any pair of nodes $u, v$ in $C$, there is a path from $u$ to $v$.

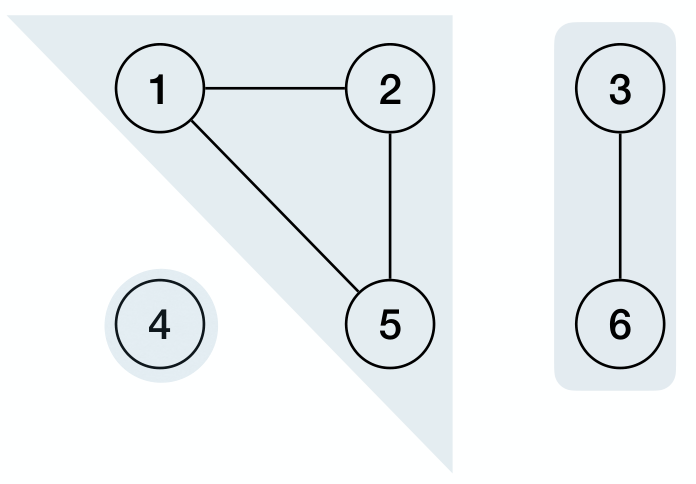
For a directed graph $G$, a strongly connected component (SCC, 强连通分量) is a maximal set $C \subseteq V(G)$, such that for any pair of nodes $u, v$ in $C$, there is a directed path from $u$ to $v$ and a path from $v$ to $u$, and vice versa.

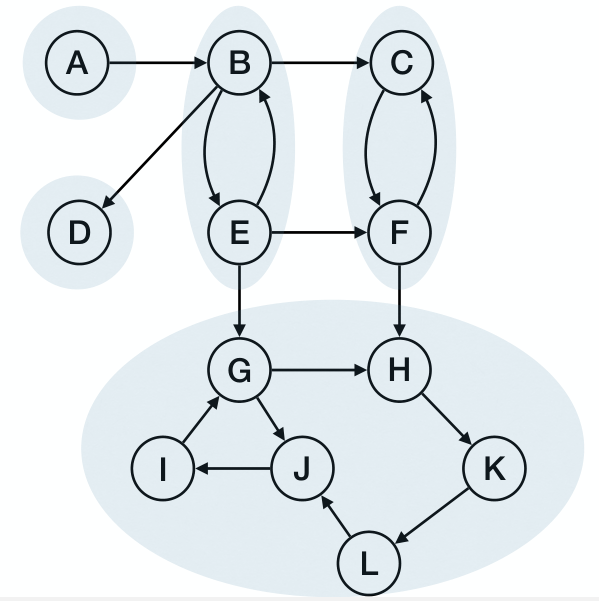
Given an undirected graph, just do DFS or BFS on the entire graph can compute its CC.

However for a directed graph, it's not that easy.

Component Graph & Computing SCC

Given a directed graph $G = (V, E)$, assume it has $k$ SSC $\left\lbrace C_i \right\rbrace$. Then the component graph is $G^C = (V^C, E^C)$.

• The vertex set $V^C = \left\lbrace v_1, \cdots, v_k \right\rbrace$, each representing one SCC.
• There is an edge $(v_i, v_{j}) \in E^C$ if there exists $(u, v) \in E$ where $u \in C_i, v \in C_j$.

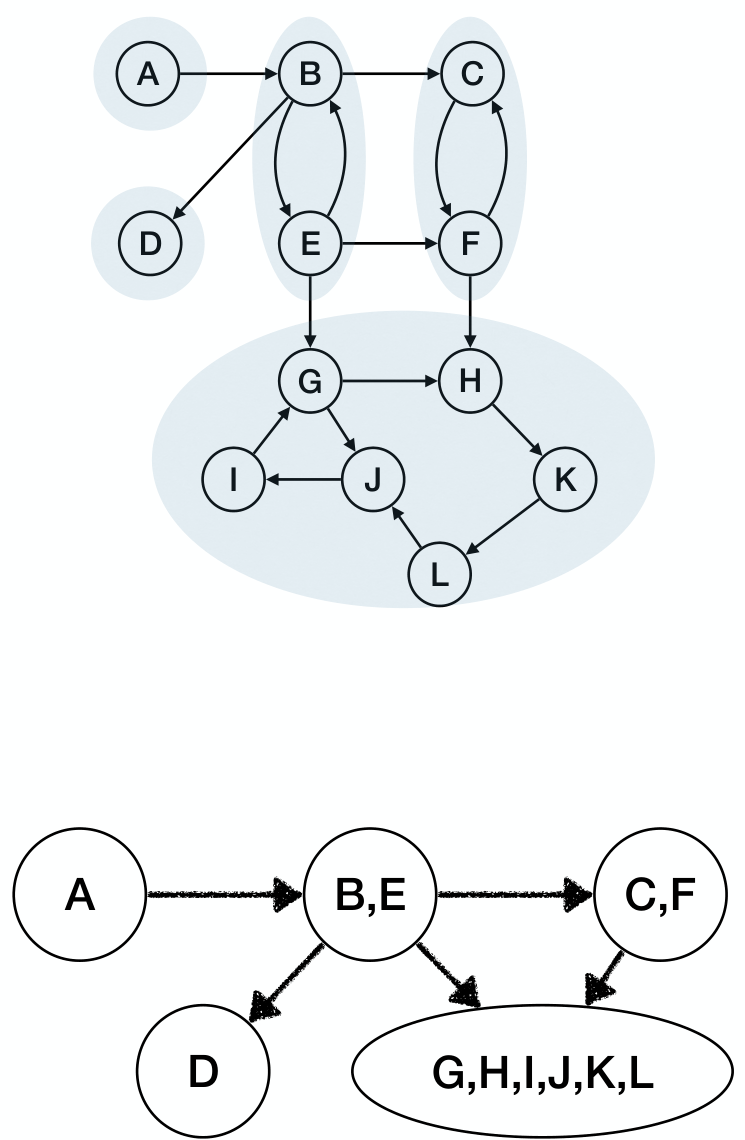
Claim: A component graph is a DAG. Otherwise the components in the circle becomes a bigger SCC, contradicting the maximality of SCC.

Since each DAG has at least one source and one sink, we can do one DFS starting from a node in a sink SCC, and explore exactly nodes in that SCC and stop.

However:

1. How to identify a node that is in a sink SCC?
   • We don't know the structure of component graph.
   • The node with earliest finished time is not always in a sink SCC.
2. What to do when the first SCC is done?

Though the node with earliest finished time is not always in a sink SCC, the node with latest finished time is always in a source SCC.

Therefore, we can reverse the direction of each edge in $G$ getting $G^R$, then the sink SCC in $G^C$ is the source SCC in $(G^R)^C$.

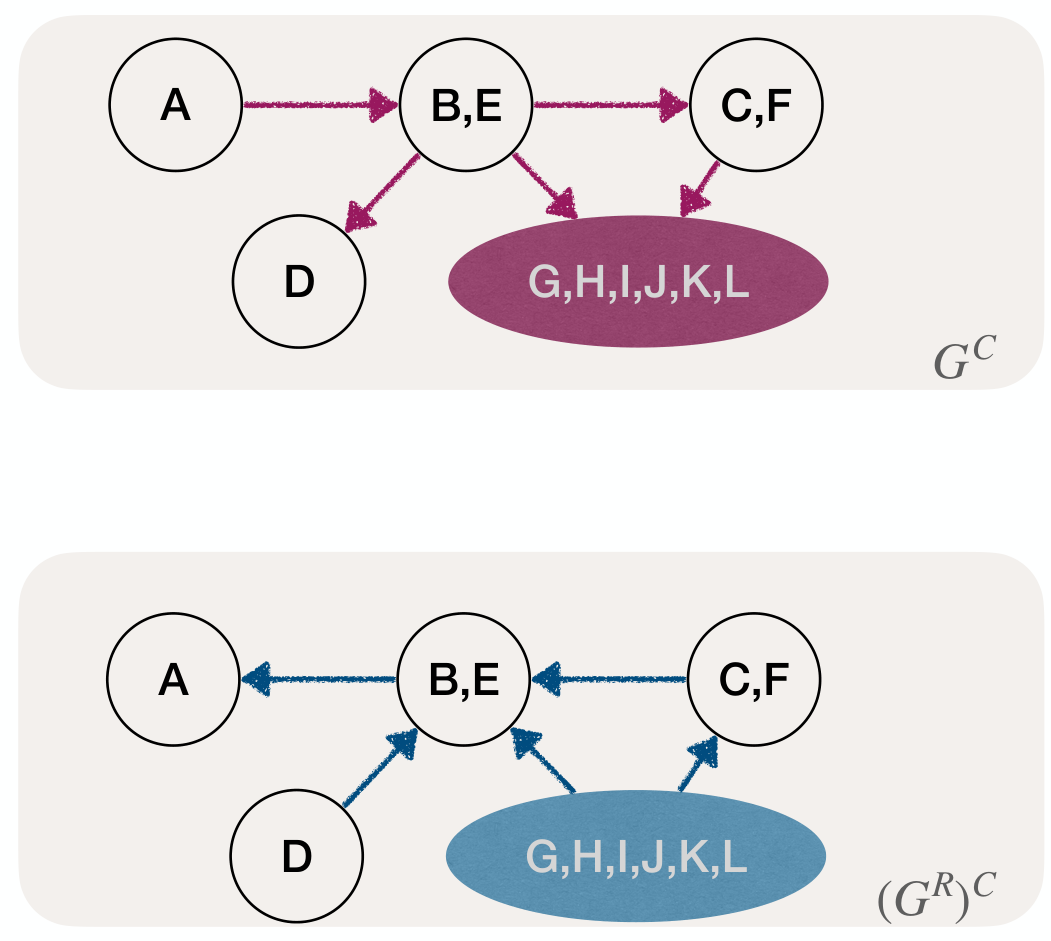
Compute $G^R$ in $O(n+m)$ time, then find a node is a source SCC in $G^R$. Do DFS in $G^R$, the nod ewith maximum finish time is guaranteed to be in source SCC.

Lemma

For any edge $(u, v) \in E(G^R)$, if $u \in C_i, v \in C_{j}$, then $\max\limits_{u \in C_i} \left\lbrace u.f \right\rbrace > \max\limits_{v \in C_{j}}\left\lbrace v.f \right\rbrace$.

Proof.

Consider nodes in $C_i$ and $C_j$, let $w$ be the first node visited by DFS.

If $w \in C_{j}$, then all nodes in $C_{j}$ will be visited before any nodes in $C_i$ is visited. In this case, the lemma is true.

If $w \in C_i$, at the time that DFS visits $w$, for any node in $C_i, C_{j}$, there is a white-path from $w$ to that node. In this case, due to the white-path theorem, the lemma again holds.

The second question. For remaining nodes in $G$, the node with max finish time (in DFS of $G^R$) is again in a sink SCC for whatever remains of $G$.

Tarjan's Algorithm*

这个部分纯听了，不记了。

Minimum Spanning Trees

最小生成树部分一样可以参考《离散数学》笔记关于「生成树」的内容。

Consider a connected, undirected, weighted graph $G$. That is, we have a graph $G = (V, E)$ together with a weight function $w\colon E \to\R$ that assigns a real weight $w(u, v)$ to each edge $(u, v) \in E$.

A spanning tree(生成树) of $G$ is a tree containing all nodes in $V$ and a subset of all the edges $E$.

A minimum spanning tree(最小生成树, MST) is a spanning tree whose total weight $w(T) = \displaystyle \sum_{(u, v) \in T}w(u, v)$ is minimized.

Kruskal's Algorithm

Kruskal 算法：从空集开始，每次加入权重最小的安全边，直到生成树。

Identifying Safe Edges

A cut(割) $(S, V-S)$ of $G = (V, E)$ is a partition of $V$ into two parts.

An edge crosses the cut $(S, V - S)$ if one of its endpoint is in $S$ and the other endpoint is in $V-S$.

A cut respects an edge set $A$ if no edge in $A$ crosses the cut.

An edge is a light edge crossing a cut if the edge has minimum weight among all edges crossing the cut.

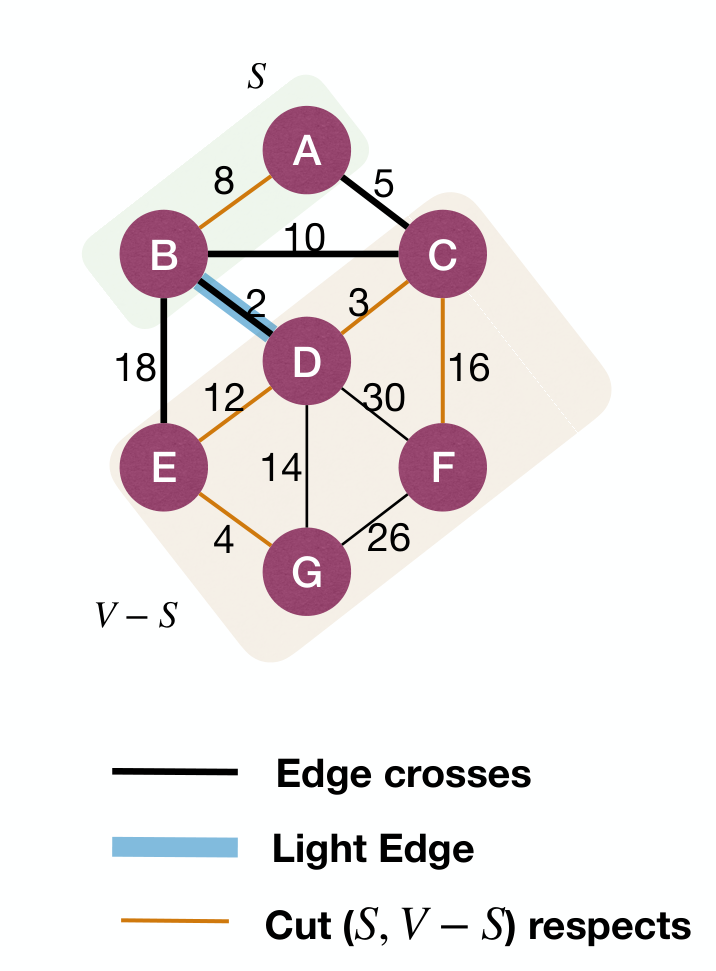
Cut Property

Assume $A$ is included in the edge set of some MST, let $(S, V - S)$ be any cut respecting $A$. If $(u, v)$ is a light edge crossing the cut, then $(u, v)$ is safe for $A$.

Proof.

Proof PPT:

Corollary: Assume $A$ is included in some MST, let $G_A = (V, A)$. Then for any connected component in $G_A$, its minimum-weight-outgoing-edge^outgoing in $G$ is safe for $A$.

Strategy for finding safe edge in Kruskal's algorithm: Find minimum weight edge connecting two CC in $G_A$.

KruskalMST(G):
A := {}
Sort edges into weight increasing order
for each edge (u, v) taken in weight increasing order
    if adding edge (u, v) does not form cycle in A
        A := A + {(u, v)}
return A

Put another way:

1. Start with $n$ CC, each node itself is a CC. And $A = \empty$.
2. Find minimum weight edge connecting two CC. Then the number of CC is reduced by 1.
3. Repeat until one CC remain.

Kruskal's Algorithm process:

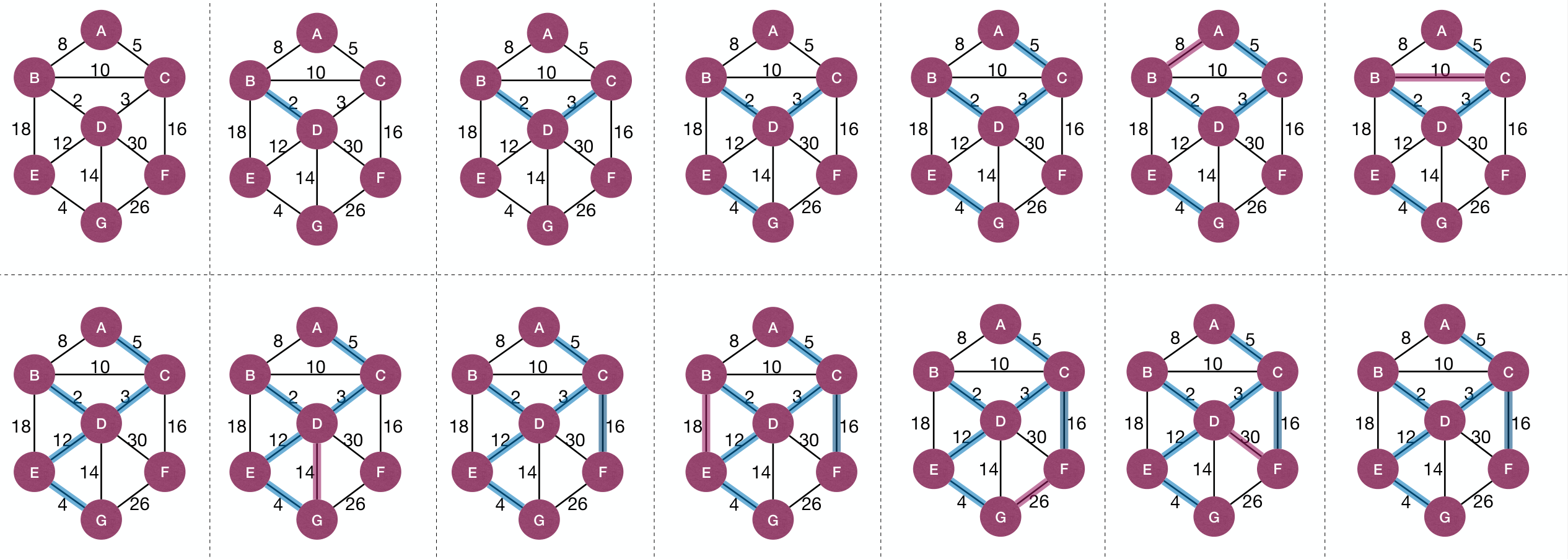
How to determine an edge forms a cycle? Put another way, how to determine if the edge is connecting two CC?

The answer is using disjoint-set data structure. Each set is a CC, $u$ and $v$ in same CC if Find(u) = Find(v).

KruskalMST(G, w):
A := {}
Sort edges into weight increasing order
for each node u in V
    MakeSet(u)
for each edge (u, v) taken in weight increasing order
    if Find(u) != Find(v)
        A := A + {(u, v)}
        Union(u, v)
return A

Runtime of Kruskal's Algorithm: $O(m \log n)$ when using disjoint-set data structure.

一开始想过，为何不可以维护一个集合，包含当前解答中含有的顶点，若新的边包含两个顶点都在这个集合中，说明会形成环，不加入解答。这样就不需要并查集了。

实际上这是不正确的，关键在于「两个顶点都在集合中，会形成环」这是不正确的。有可能这两个顶点分别在两个连通分支上，这时候就需要加入这条边。

参考了 Could Kruskal’s algorithm be implemented in this way instead of using a disjoint-set forest? 中的解答。

Prim's Algorithm

Prim Algorithm: Keep find MWOE in one fixed CC in $G_A$.

PrimMST(G, w):
A := {}
Cx := {x}
while Cx is not a spanning tree
    Find MWOE (u, v) of Cx
    A := A + {(u, v)}
    C := C + {v}
return A

Put another way:

1. Start with $n$ CC, each node itself is a CC. And $A = \empty$.
2. Pick a node $x$.
3. Find MWOE of the component containing $x$. The number of CC is reduced by 1.
4. Repeat until one CC remain.

Prim's Algorithm process:

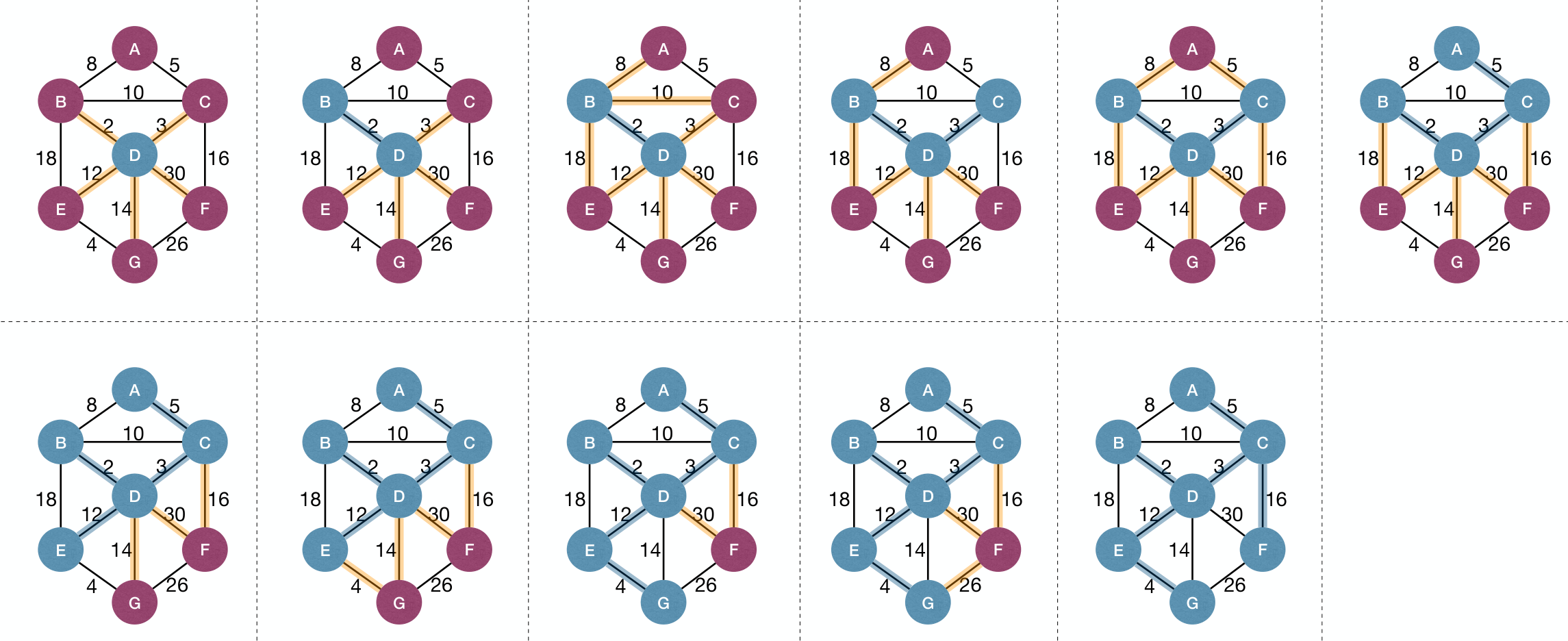
How to find MWOE efficiently? Put another way, how to find the next node that is closest to $C_x$?

The answer is using a priority queue to maintain each remaining node's distance to $C_x$.

PrimeMST(G, w):
x := Pick an arbitrary node in G
for each node u in V
    u.dist := INF
    u.parent := NIL
    u.in := False
x.dist := 0
PriorityQueue Q := Build a priority queue based on 'dist' values.
while Q is not empty
    u := Q.ExtractMin()
    u.in := True
    for each edge (u, v) in E
        if v.in = False and w(u, v) < v.dist
            v.parent := u
            v.dist := w(u, v)
            Q.Update(v, w(u, v))

$O(m \log n)$ using binary heap to implement priority queue.

Borůvka's Algorithm

The earliest MST algorithm.

1. Starting with all nodes and an empty set of edges $A$.
2. Find MWOE for every remaining CC in $G_A$, add all of them to $A$.
3. Repeat above step until we have a spanning tree.

Borůvka's Algorithm process:

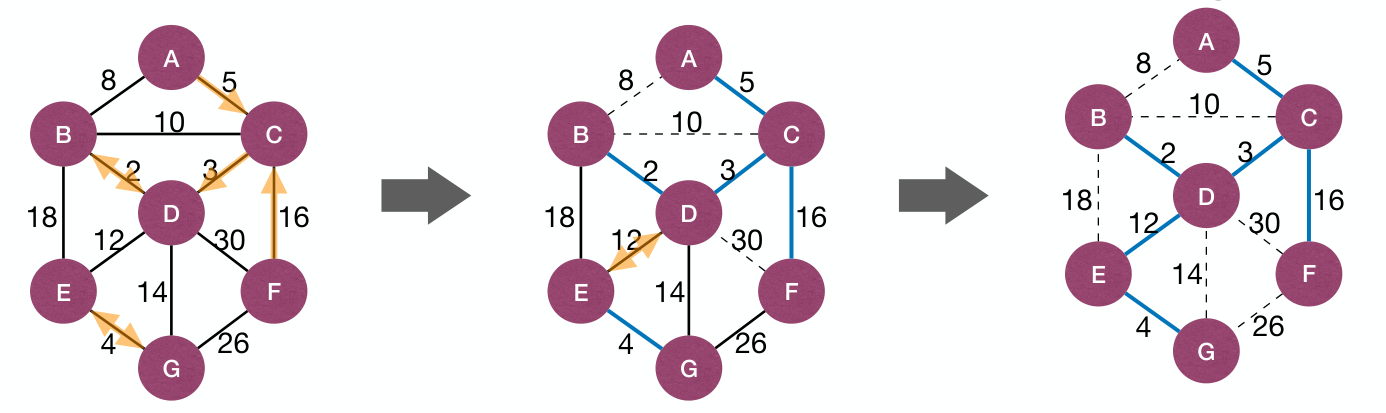
It's okay to add multiple edges simultaneously. Pick each CC at one time and it's safe:

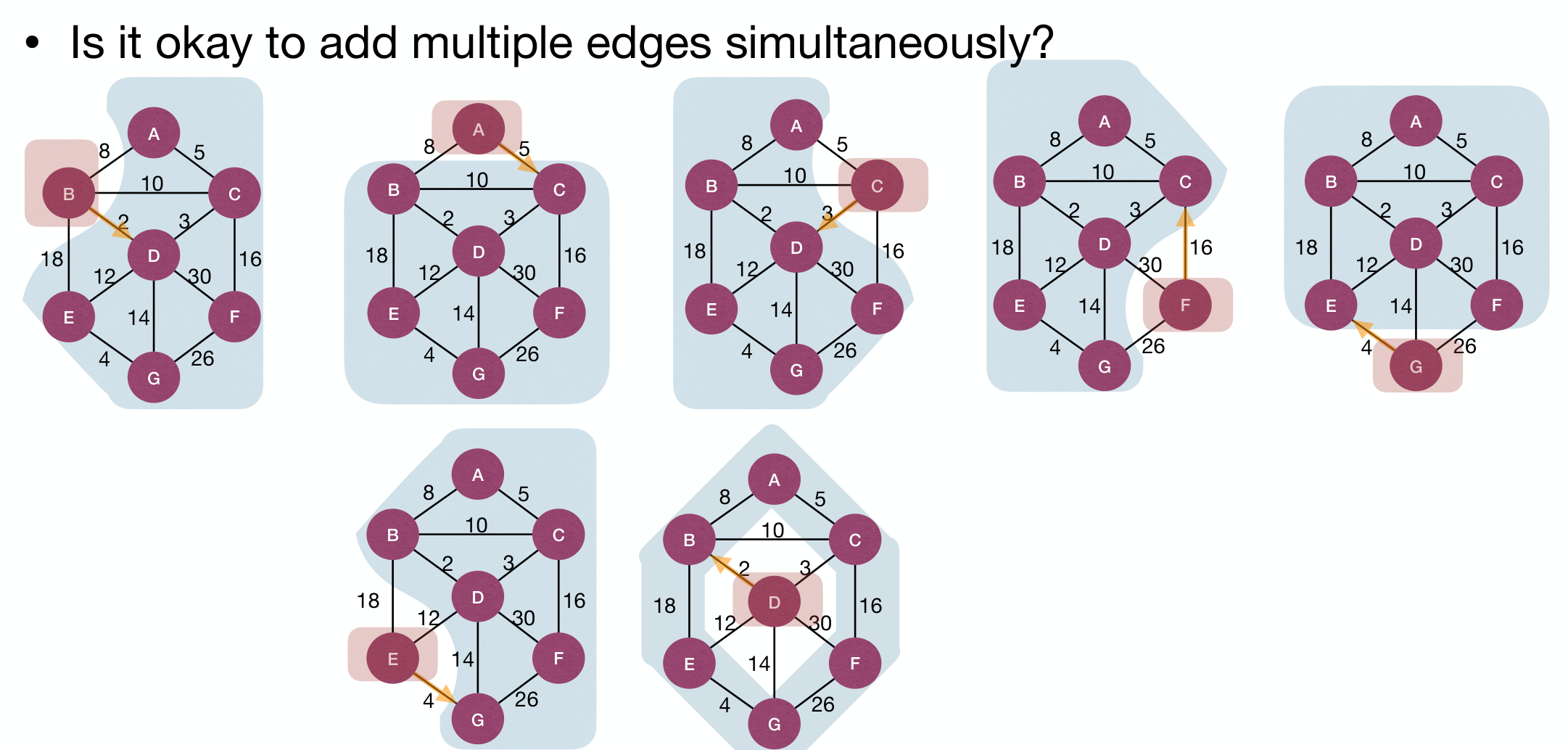
But may it result in circles?

Assume all weights of edges are distinctly, if CC $C_1$ propose MWOE $e_1$ to connect $C_2$, and $C_2$ proposes MWOE $e_2$ to connect $C_1$, then $e_1 = e_2$.

BoruvkaMST(G, w):
G' := (V, {})
do
    // Do DFS/BFS, count numbers of CC, give ccNum-th to nodes
    ccCount := CountCCAndLabel(G') // O(n)
    for i := 1 to ccCount // O(n)
        safeEdge[i] := NIL
    for each edge (u, v) in E(G) // O(m + n) = O(m)
        if u.ccNum != v.ccNum
            if safeEdge[u.ccNum] = NIL or w(u, v) < w(safeEdge[u.ccNum])
                safeEdge[u.ccNum] := (u, v)
            if safeEdge[v.ccNum] = NIL or w(u, v) < w(safeEdge[v.ccNum])
                safeEdge[v.ccNum] := (u, v)
        for i := 1 to ccCount // O(n)
            Add safeEdge[i] to E(G')
while ccCount > 1 // O(log n) interactions
return E(G')

$O(\log n)$ because we at least combine two CC into one CC for each CC in one iteration.

Borůvka’s algorithm allows for parallelism naturally; while the other two are intrinsically sequential.

Randomized algorithm with expected $O(m)$ runtime exists.