机器翻译

发表于 2025-04-18 Waline：阅读次数：本文字数： 7.2k 阅读时长 ≈ 26 分钟

概述

定义与目标

机器翻译

机器翻译（Machine Translation, MT）是指利用计算机将一种自然语言（源语言，Source Language）自动翻译为另一种自然语言（目标语言，Target Language）的过程。它是自然语言处理（NLP）领域中历史最悠久、也是最具挑战性的核心任务之一。

历史背景：机器翻译的想法由来已久，可追溯至 17 世纪笛卡尔等人提出的通用语言符号构想。现代研究始于 20 世纪 40-50 年代，Warren Weaver 在 1947 年提出利用计算机进行翻译的可能性，Bar-Hillel 等人则在 1951 年开始了早期研究，并于 1952 年组织了首届国际机器翻译会议。
任务目标：给定源语言句子 $s$ ，找到最合适的目标语言句子 $t$ 。

发展历程

机器翻译的发展大致经历了三个主要阶段：

基于规则的机器翻译（Rule-based Machine Translation, RBMT）
- 核心思想：依赖语言学家手工编写的翻译规则（包括词典、语法规则、转换规则等）。认为每一种语义在不同的语言当中都存在与其相对应的符号。
- 过程：通常涉及词汇替换，并利用两种语言的句法规则来调整词序和结构。
- 局限性：
  - 规则库构建成本高昂，维护困难。
  - 难以覆盖复杂多样的语言现象，规则间易产生冲突。
  - 对歧义和语境的处理能力有限，翻译质量往往不高，尤其在面对大规模真实文本时。
基于统计的机器翻译（Statistical Machine Translation, SMT）
- 核心思想：从大规模平行语料库（成对的源语言和目标语言句子）中自动学习翻译知识，采用数据驱动的方法。
- 过程：通过统计模型找到源语言片段（单词或短语）与目标语言片段的最可能对应关系。主流方法包括基于词的 SMT 和基于短语的 SMT。
- 优势：相比 RBMT，能够更好地处理真实文本，翻译流畅度有所提升。在 2000 年代至 2010 年代中期是主流方法。
- 步骤：通常包括预处理、句子对齐、词对齐、短语抽取、特征准备、语言模型训练等。
基于神经网络的机器翻译（Neural Machine Translation, NMT）
- 核心思想：使用深度神经网络（尤其是 Seq2Seq 架构）直接建模从源语言到目标语言的端到端映射。
- 优势：
  - 强大的表示学习能力，减少了对语言学特征工程的依赖。
  - 能够更好地捕捉长距离依赖和上下文信息。
  - 端到端训练，系统结构更简洁。
  - 显著提升了翻译的流畅度和准确性，成为当前最先进的方法。

现状与挑战

性能：NMT 在特定领域和受控条件下已达到非常高的水平，有时甚至接近专业人工翻译。例如，在 WMT (Workshop on Machine Translation) 评测中，顶尖系统得分很高。
局限：在开放域和复杂文本上，MT 结果仍与人工翻译的「信达雅」标准有较大差距。
- 信（Faithfulness）：忠实于原文。
- 达（Expressiveness）：表达清晰流畅。
- 雅（Elegance）：语言优美得体。

人工翻译 vs. 机器翻译示例

Youth is not a time of life; it is a state of mind; it is not a matter of rosy cheeks, red lips and supple knees; it is a matter of the will, a quality of the imagination, a vigor of the emotions; it is the freshness of the deep springs of life. —— Samuel Ullman, Youth

青春不是生命的时光；这是一种心态；这不是红润的脸颊、红润的嘴唇和柔软的膝盖；这是意志的问题，是想象力的质量，是情感的活力；它是生命深泉的清新。——机器翻译（示例）

青春不是年华，而是心境；青春不是桃面、丹唇、柔膝，而是深沉的意志，恢宏的想象，炙热的感情；青春是生命的深泉在涌流。——人工翻译结果（王佐良译）

可以看出，机器翻译虽然基本传达了原文意思，但在语言的凝练、意境和美感上与优秀的人工翻译仍有差距。

青春并非生命旅程中的某段时光，而是一种心境；它不关乎粉面桃腮、红唇粉膝，而是意志的淬炼、想象的驰骋、情感的激荡；它是生命深处源泉涌动的勃勃生机。——Gemini 2.5 Flash

主要挑战：

自然语言复杂度高：语言具有歧义性、多变性、隐含性和不断发展的特性。即使是巨大的模型（如参数量达 1.75 万亿）也难以完全捕捉其复杂性。
翻译结果不可解释：NMT 模型（尤其是 Transformer）如同「黑箱」，其内部决策过程难以理解，无法像人一样解释翻译原因。
翻译结果评测困难：语言的灵活性导致一个句子可以有多种合理的翻译。自动评测指标（如 BLEU）与人工评价存在差距，而人工评测成本高昂且主观性强。

基于统计的机器翻译（SMT）

SMT 在很长一段时间内是机器翻译的主流方法，理解其核心思想对于了解 MT 的发展至关重要。

核心思想：噪声信道模型

SMT 常基于噪声信道模型（Noise Channel Model）构建。该模型将翻译过程视为一个信息传输问题：假设目标语言句子 $t$ 是原始信号（信源），在通过一个带噪声的信道（翻译过程）后，变成了我们观察到的源语言句子 $s$ （信宿）。

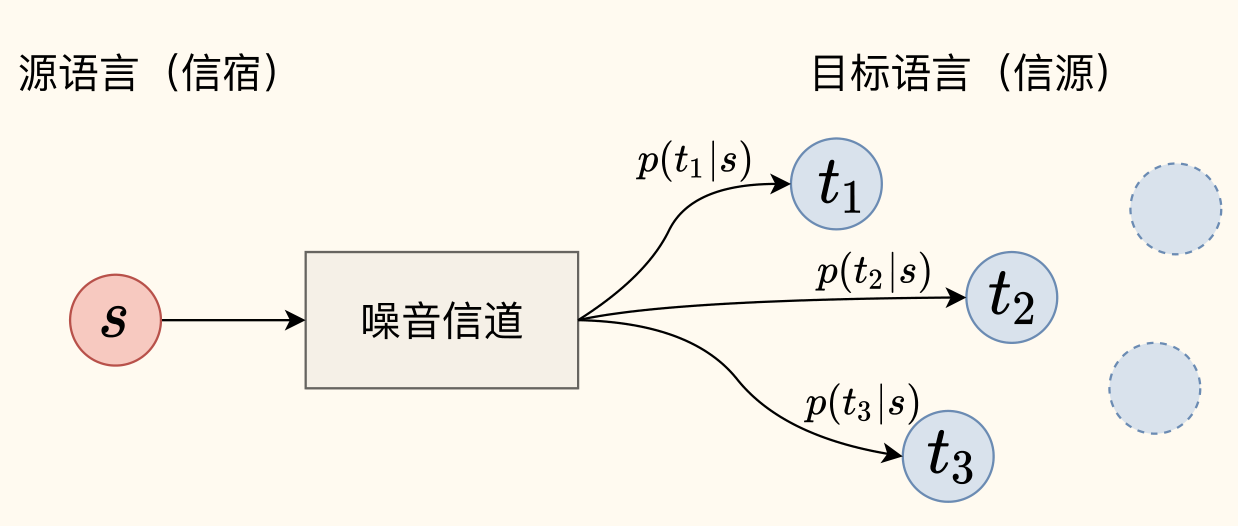
目标：给定源语言句子 $s$ ，找到最可能的目标语言句子 $\hat{t}$ 。
$\hat{t} = \argmax_t P(t\mid s)$
贝叶斯定理应用：直接计算 $P(t\mid s)$ 很困难。应用贝叶斯定理进行转换：
$P(t\mid s) = \frac{P(s\mid t)P(t)}{P(s)}$
最终优化目标：由于 $P(s)$ 对于所有候选 $t$ 都是常数，不影响最大化结果，因此可以忽略。优化目标变为：
$\hat{t} = \argmax_t P(s\mid t)P(t)$

SMT 核心组件

翻译模型 $P(s\mid t)$ ：给定目标语言句子 $t$ ，生成源语言句子 $s$ 的概率。它衡量了 $s$ 和 $t$ 在语义上的匹配程度（从 $t$ 翻译回 $s$ 的可能性）。
语言模型 $P(t)$ ：目标语言句子 $t$ 自身出现的概率。它衡量了句子 $t$ 是否符合目标语言的语法规范和表达习惯，即流畅度。

三大核心问题

在噪声信道框架下，SMT 需要解决三个核心问题：

建模：如何设计数学模型来计算翻译概率 $P(s\mid t)$ 和语言模型概率 $P(t)$ ？
训练：如何从平行语料库中学习模型参数（例如 $P(s\mid t)$ 中的词汇翻译概率）？
解码：给定源句子 $s$ 和训练好的模型，如何高效地搜索到使 $P(s\mid t)P(t)$ 最大的目标句子 $\hat{t}$ ？

建模核心：词对齐

直接在句子层面估计 $P(s\mid t)$ 会面临严重的数据稀疏问题，因为可能的句子组合是天文数字。

数据稀疏问题

假设词表大小为 10000，一个长度为 10 的句子就有 $10000^{10} = 10^{40}$ 种可能。任何有限的语料库都无法覆盖如此巨大的空间。

解决方案：将句子级翻译概率分解为更小的单元——「词级别」的对应关系。这就是词对齐（Word Alignment）。

词对齐定义：描述源语言句子 $s = \{s_1, s_2, \dots , s_m\}$ 中的词与目标语言句子 $t = \{t_0, t_1, \dots , t_l\}$ 中的词之间的对应关系（通常 $t_0$ 是一个特殊的 NULL 词，用于处理源词在目标语中没有对应词的情况）。

对齐表示：常用一个对齐向量 $a = \{a_1, a_2, \dots , a_m\}$ 表示，其中 $a_j = i$ 意味着源语言的第 $j$ 个词 $s_j$ 对齐到目标语言的第 $i$ 个词 $t_i$ 。

词对齐示例

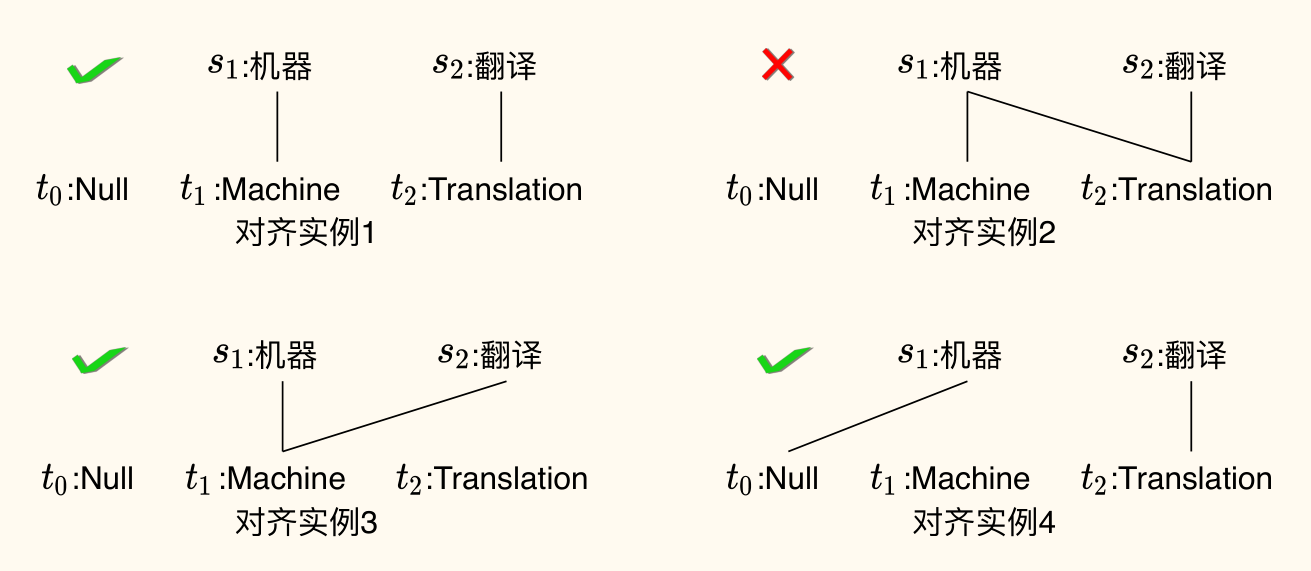
IBM 模型限制（为了简化建模）：

一对多约束：每个源语言单词最多只能对齐到一个目标语言单词（包括 NULL）。
- 注意：这限制了目标词生成多个源词的情况，后续模型会放宽
NULL 对齐：允许源语言单词对齐到 NULL 词，处理源词在目标语中无对应（如虚词、赘词）或目标语中词汇缺失的情况。

IBM 模型系列

IBM 公司提出了一系列（Model 1 到 Model 5）逐渐复杂的统计模型来解决词对齐和翻译概率 $P(s\mid t)$ 的建模问题。这些模型将句子级概率 $P(s\mid t)$ 通过引入隐变量——词对齐 $a$ 来分解：

$P(s\mid t) = \sum_{a} P(s, a\mid t)$

其中 $P(s, a\mid t)$ 表示给定目标句 $t$ ，生成源句 $s$ 及其对齐 $a$ 的联合概率。

进一步使用链式法则分解 $P(s, a\mid t)$ ：

$P(s, a\mid t) = P(m\mid t) \prod_{j=1}^{m} P(a_j \mid a_1^{j-1}, s_1^{j-1}, m, t) P(s_j \mid a_j, s_1^{j-1}, m, t)$

这个公式描述了一个生成过程：

给定 $t$ ，确定源句长度 $m$ （概率 $P(m\mid t)$ ）。
对于源句的每个位置 $j$ $j$ （从 $1$ $1$ 到 $m$ $m$ ）：
1. 确定该位置的词 $s_j$ 应该对齐到目标句的哪个位置 $a_j$ （对齐概率 $P(a_j\mid \dots )$ ）。
2. 根据对齐位置 $a_j$ 和之前的状态，生成源词 $s_j$ （词汇生成概率 $P(s_j\mid \dots )$ ）。

IBM 模型系列的主要区别在于对 $P(m\mid t)$ 、 $P(a_j\mid \dots )$ 和 $P(s_j\mid \dots )$ 做了不同程度的简化假设。

IBM Model 1（基础与简化）

核心假设：

长度概率 $P(m\mid t) = \epsilon$ （一个常数，与 $t$ 和 $m$ 无关）。
对齐概率 $P(a_j \mid a_1^{j-1}, s_1^{j-1}, m, t) = \dfrac{1}{l+1}$ （均匀分布，每个源词等概率地对齐到目标词的任一位置或 NULL）。
词汇生成概率 $P(s_j \mid a_j, s_1^{j-1}, m, t) = f(s_j \mid t_{a_j})$ （只依赖于其对齐的目标词）。

最终公式：

$\begin{aligned} P(s\mid t) &= \sum_{a} P(s, a\mid t) \\ &= \sum_{a} \epsilon \prod_{j=1}^{m} \frac{1}{l+1} f(s_j \mid t_{a_j}) \\ &= \frac{\epsilon}{(l+1)^m} \sum_{a} \prod_{j=1}^{m} f(s_j \mid t_{a_j}) \end{aligned}$

计算技巧：直接对所有 $(l+1)^m$ 种对齐求和复杂度太高。利用求和与连乘的可交换性：

$\sum_{a} \prod_{j=1}^{m} f(s_j \mid t_{a_j}) = \sum_{a_1=0}^{l} \dots \sum_{a_m=0}^{l} \prod_{j=1}^{m} f(s_j \mid t_{a_j}) = \prod_{j=1}^{m} \sum_{i=0}^{l} f(s_j \mid t_i)$

因此，简化后的 Model 1 翻译概率为：

$P(s\mid t) = \frac{\epsilon}{(l+1)^m} \prod_{j=1}^{m} \sum_{i=0}^{l} f(s_j \mid t_i)$

计算复杂度从 $O((l+1)^m)$ 降为 $O(m \cdot l)$ 。

训练：词汇翻译概率 $f(s\mid t)$ 是模型参数，通常使用「EM 算法」从平行语料中进行无监督学习（因为对齐关系 $a$ 是未知的隐变量）。
缺点：对齐概率均匀分布的假设过于简单，不符合实际语言中词语位置的对应倾向。

IBM Model 2（引入对齐位置）

改进点：对齐概率不再是均匀的，而是依赖于源词位置 $j$ 、源句长度 $m$ 和目标句长度 $l$ 。

$P(a_j \mid a_1^{j-1}, s_1^{j-1}, m, t) = a(a_j \mid j, m, l)$

其中 $a(i \mid j, m, l)$ 是新的模型参数，表示源句位置 $j$ 的词对齐到目标句位置 $i$ 的概率。

公式：

$P(s\mid t) = \epsilon \sum_{a} \prod_{j=1}^{m} a(a_j \mid j, m, l) f(s_j \mid t_{a_j})$

同样可以利用计算技巧简化：

$P(s\mid t) = \epsilon \prod_{j=1}^{m} \sum_{i=0}^{l} a(i \mid j, m, l) f(s_j \mid t_i)$

优点：考虑了词语的位置信息，对齐效果优于 Model 1。参数 $a$ 和 $f$ 同样使用 EM 算法学习。

IBM Model 3（引入繁衍率）

动机：Model 1 和 2 不能很好地处理一个目标词对应多个源词的情况（一对多对齐）。

关键概念：

繁衍率（Fertility） $\phi_i$ ：目标词 $t_i$ 生成（对齐到）的源词个数。引入繁衍率概率 $n(\phi \mid t_i)$ 。
词汇生成概率 $t(s_j \mid t_{a_j})$ ：与 Model 1/2 中的 $f$ 类似。
扭曲度（Distortion） $d(j \mid a_j, m, l)$ ：源词 $s_j$ 出现在位置 $j$ 的概率，给定它对齐到 $t_{a_j}$ 以及句子长度 $m, l$ 。这反映了词序调换的可能性。

模型会变更复杂，因为涉及为每个目标词分配繁衍数、为每个生成的源词槽选择一个源词、为每个源词确定位置。

公式概览：

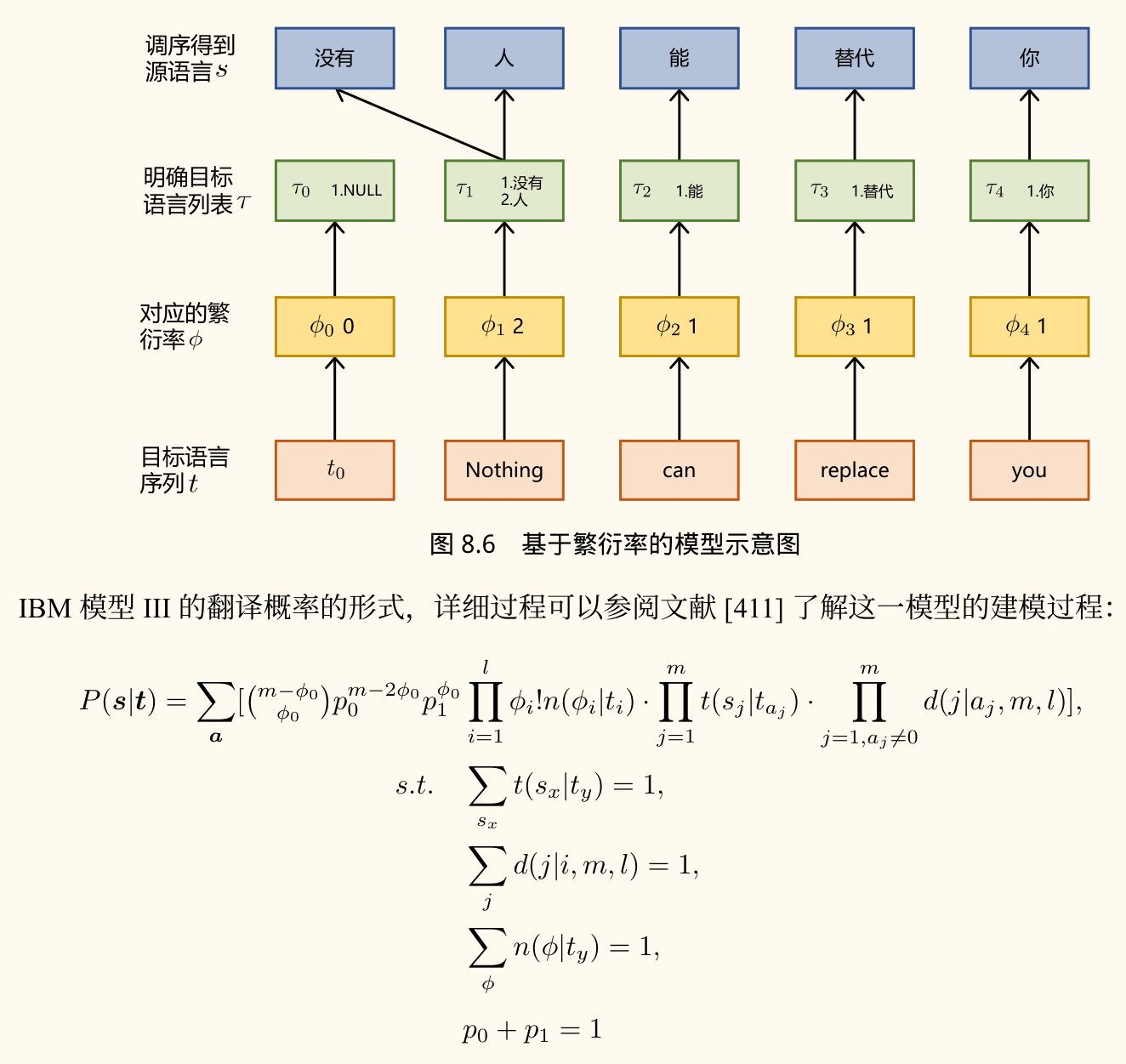
能更好地建模一对多对齐和词序变化。

IBM Model 4（改进扭曲度）

动机：Model 3 的扭曲度模型仍然比较简单，没有考虑词与词之间的相对位置。

改进点：

将扭曲度建模为相对位置。生成第 $j$ 个源词的位置依赖于上一个生成的对齐到同一个目标词的源词的位置，或者依赖于对齐到上一个目标词的源词的平均位置。
引入词类信息 $A(\cdot), B(\cdot)$ ，使得扭曲度与词的类别相关。

关键概念：

概念（Concept）：非空对齐的目标语言单词。
扭曲度函数 $d_1$ (第一个词) 和 $d_{>1}$ (后续词) 依赖于相对偏移量和词类。

效果：更精细地建模了词序变化，尤其是在局部范围内。

IBM Model 5（解决对齐冲突）

动机：Model 3 和 4 在放置源词时，可能会将多个词放在同一个位置上（对齐冲突）。

关键改进：引入空位检查机制。在放置每个源词 $s_j$ 到位置 $k$ 时，检查该位置 $k$ 是否已经被占用。如果已被占用，则该对齐的概率为 0。

效果：确保生成的对齐是有效的（一个位置只有一个词），模型更加完善。

IBM 模型总结

IBM 模型 1-5 是一个逐步复杂化的过程，不断引入新的参数和假设来更精确地建模词对齐和翻译过程中的各种现象（位置、一对多、词序、冲突）。通常先用简单模型（如 Model 1）初始化，再用复杂模型（如 Model 4 或 HMM 对齐模型）进行训练。

解码（Decoding）

在训练好翻译模型 $P(s\mid t)$ 和语言模型 $P(t)$ 后，解码的目标是找到最优翻译 $\hat{t}$ ：

$\hat{t} = \argmax_t P(s\mid t)P(t)$

这是一个巨大的搜索空间。

挑战：目标语言句子 $t$ 的可能性非常多，无法穷举。

常用算法：

贪婪解码：每一步选择当前最优的词，简单但容易陷入局部最优。
集束搜索：每一步保留 K 个最可能的候选部分翻译，在 K 个候选中扩展下一步，再选出新的 K 个最优候选。是 SMT 和 NMT 中最常用的近似搜索算法。

基于神经网络的机器翻译（NMT）

NMT 的出现是机器翻译领域的重大突破，目前已成为主流方法。

从 SMT 到 NMT：动机与优势

SMT 的局限性：

复杂的特征工程：SMT 系统通常包含大量人工设计的特征，依赖语言学知识。
组件繁多：系统由翻译模型、语言模型、调序模型等多个独立训练的模块组成，难以联合优化。
错误累积：流水线式的处理流程可能导致早期模块的错误传递并放大。
上下文建模受限：语言模型通常基于马尔可夫假设（如 N-gram），难以捕捉长距离依赖；基于短语的方法也忽略了短语外的依赖。

NMT 的优势：

端到端训练：将翻译视为一个单一的、整体的神经网络模型进行训练，能够更好地进行全局优化。
自动特征学习：神经网络能自动从数据中学习有效的特征表示，减少了对人工特征工程和语言学知识的依赖。
更好的上下文建模：RNN、CNN、Transformer 等结构能更有效地捕捉长距离依赖和上下文信息。
更高的翻译质量：在流畅度和忠实度上通常优于 SMT 系统。

基本框架：序列到序列（Seq2Seq）

大多数 NMT 模型基于编码器-解码器（Encoder-Decoder）的 Seq2Seq 架构。

graph LR
    A[源语言序列 S] --> B(编码器 Encoder);
    B --> C{上下文表示 C};
    C --> D(解码器 Decoder);
    D -- 已生成的部分翻译 --> D;
    D --> E[目标语言序列 T];

编码器（Encoder）：读取源语言句子 $S = (s_1, \dots , s_n)$ ，将其压缩成一个（或一系列）包含其语义信息的上下文表示 $C$ 。
解码器（Decoder）：根据上下文表示 $C$ 和已经生成的目标词序列 $(t_1, \dots , t_{i-1})$ ，预测下一个目标词 $t_i$ 。这个过程是自回归的，直到生成结束符 [EOS]。
数学表示：目标是最大化条件概率 $P(T\mid S)$ 。
$\hat{T} = \underset{T}{\operatorname{argmax}} P(T\mid S) = \underset{T}{\operatorname{argmax}} \prod_{i=1}^{m} P(t_i \mid t_{<i}, S)$

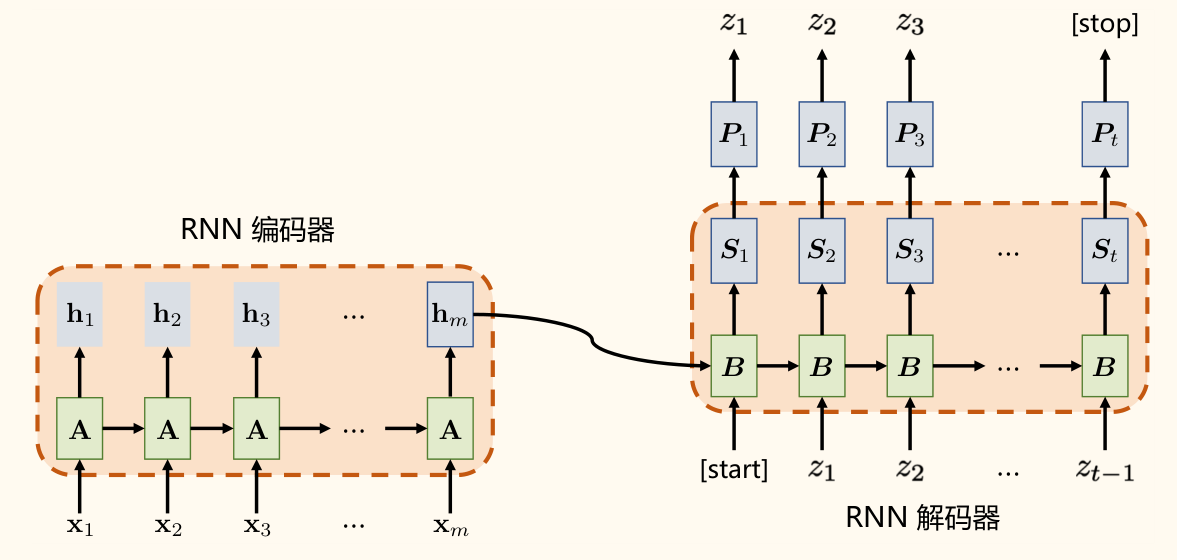
循环神经网络（RNN）翻译模型

早期的 NMT 模型主要使用 RNN（特别是 LSTM 或 GRU）来实现 Seq2Seq 架构。

编码器：一个 RNN 按顺序读取源语言词嵌入 $x_1, \dots , x_n$ ，更新其隐藏状态 $\bm{h}_t = \operatorname{RNN}_{\text{enc}}(\bm{h}_{t-1}, x_t)$ 。最终的隐藏状态 $\bm{h}_n$ 被视为整个源句的上下文表示 $C = \bm{h}_n$ 。
解码器：另一个 RNN，其初始隐藏状态 $s_0$ 通常设置为编码器的最终状态 $\bm{h}_n$ 。在每个时间步 $i$ ，它接收上一个预测的词 $t_{i-1}$ （的嵌入）作为输入，并结合当前隐藏状态 $s_{i-1}$ 来预测当前词 $t_i$ 的概率分布，并更新隐藏状态 $s_i = \operatorname{RNN}_{\text{dec}}(s_{i-1}, t_{i-1})$ 。通常使用特殊的 [Start] 符号启动解码。
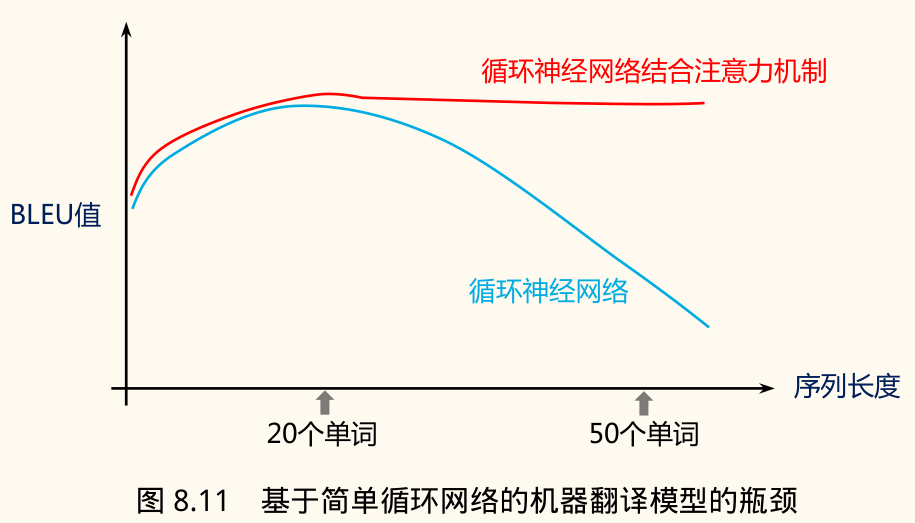
信息瓶颈问题：将整个源句信息压缩到一个固定大小的向量 $\bm{h}_n$ 中，对于长句子来说，这个向量可能无法承载所有必要信息，导致信息丢失。性能会随着句子长度增加而下降（如课件 Page 40 蓝线所示）。

注意力机制（Attention）

为了解决信息瓶颈问题，引入了注意力机制。

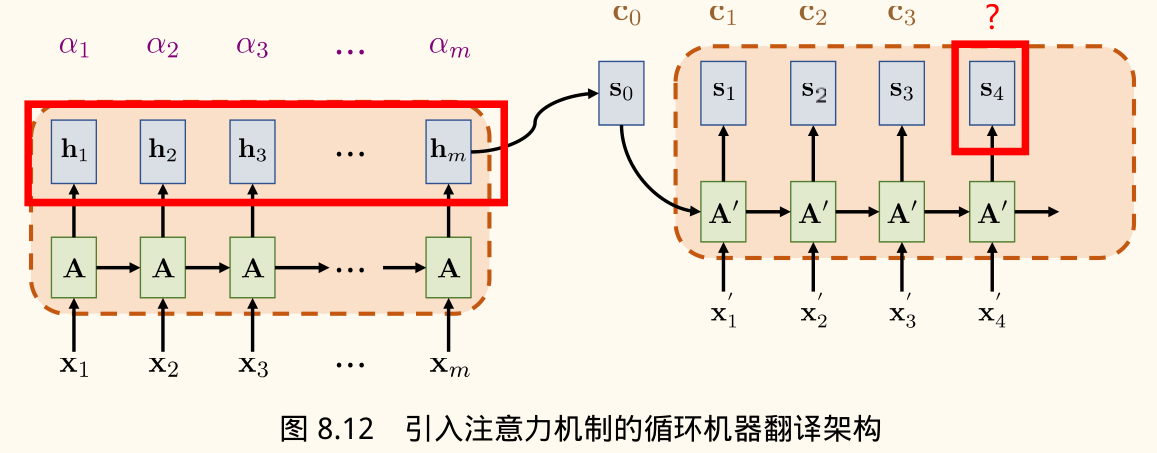
核心思想：允许解码器在生成每个目标词时，动态地「关注」源语言句子的不同部分，而不是仅依赖于编码器最后的固定向量。
原理：解码器不再只使用编码器最后一个状态 $\bm{h}_n$ ，而是利用编码器所有时间步的隐藏状态 $\bm{H} = (\bm{h}_1, \dots , \bm{h}_n)$ 。
计算流程（在解码第 $i$ $i$ 个目标词时）：
1. 计算对齐分数：计算当前解码器状态 $\bm{s}_{i-1}$ $s_{i - 1}$ 与每个编码器隐藏状态 $\bm{h}_j$ $h_{j}$ 之间的相关性得分 $e_{ij} = \operatorname{score}(\bm{s}_{i-1}, \bm{h}_j)$ $e_{ij} = score (s_{i - 1}, h_{j})$ 。
  - 常用打分函数：点积 $\bm{s}_{i-1}^\intercal \bm{h}_j$ 、双线性 $\bm{s}_{i-1}^\intercal \bm{W} \bm{h}_j$ 、加性 $\bm{v}^\intercal \tanh(\bm{W}_s \bm{s}_{i-1} + \bm{W}_h \bm{h}_j)$ 等。
2. 计算注意力权重：对分数进行 Softmax 归一化，得到表示关注程度的权重 $\alpha_{ij}$ 。
  $\alpha_{ij} = \frac{\exp(e_{ij})}{\sum_{k=1}^{n} \exp(e_{ik})}$
3. 计算上下文向量：将编码器的隐藏状态按注意力权重加权求和，得到当前步的上下文向量 $c_i$ 。
  $c_i = \sum_{j=1}^{n} \alpha_{ij} \bm{h}_j$
4. 结合上下文进行预测：将上下文向量 $c_i$ 与解码器的当前输入（如 $t_{i-1}$ 的嵌入）结合起来，输入解码器 RNN 单元，用于预测下一个词 $t_i$ 并更新解码器状态 $\bm{s}_i$ 。例如： $\bm{s}_i = \operatorname{RNN}_{\text{dec}}(\bm{s}_{i-1}, [t_{i-1}, c_i])$ 。

注意力机制的效果

注意力机制允许模型根据需要聚焦于源句中最相关的信息，极大地提升了 NMT 处理长句子的能力和翻译质量。

卷积神经网络（CNN）翻译模型（ConvS2S）

为了提高并行计算能力，研究者提出了使用 CNN 构建 Seq2Seq 模型。

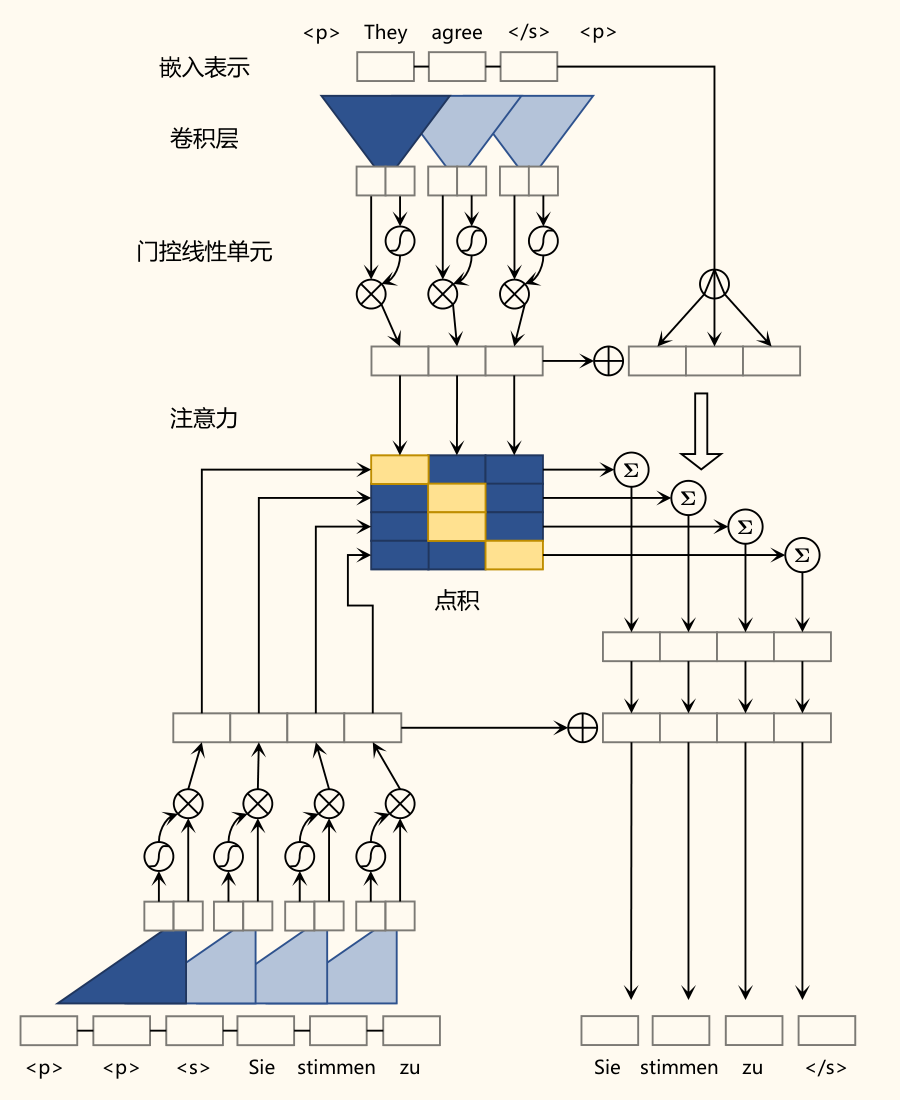
动机：CNN 的卷积操作可以在序列维度上并行计算，不像 RNN 需要顺序处理。通过堆叠卷积层可以扩大感受野，捕捉长距离依赖。
代表模型：Facebook AI 的 ConvS2S。
关键组件：
1. 位置编码：由于 CNN 本身不处理序列顺序，需要显式地为输入嵌入添加位置信息。通常使用可学习的位置嵌入或固定的正弦/余弦位置编码，与词嵌入相加。 $\bm{E} = \{\text{word\_emb}_i + \text{pos\_emb}_i\}_{i=1}^n$ 。
2. 门控卷积单元：使用门控机制增强卷积层的表达能力。通常采用 GLU(Gated Linear Unit)：对输入 $\bm{X}$ 进行卷积得到两部分 $\bm{A}$ 和 $\bm{B}$ ，输出为 $\bm{h} = \bm{A} \otimes \sigma(\bm{B})$ ，其中 $\otimes$ 是逐元素乘法， $\sigma$ 是 Sigmoid 函数。这允许模型控制哪些信息可以通过。
3. 残差连接：将每一卷积层的输入直接加到其输出上 $\bm{h}^l = \operatorname{ConvGLU}(\bm{h}^{l-1}) + \bm{h}^{l-1}$ 。这有助于梯度传播，缓解深度网络训练困难的问题。
4. 多步注意力机制：在解码器的每一层都计算注意力。第 $l$ $l$ 层的解码器状态 $\bm{z}_i^l$ $z_{i}^{l}$ 会与编码器的输出 $\bm{h}_j$ $h_{j}$ （通常还会结合源词嵌入 $\bm{e}_j$ $e_{j}$ ）计算注意力权重 $a_{ij}^l$ $a_{ij}^{l}$ ，得到该层的上下文向量 $\bm{c}_i^l = \sum_j a_{ij}^l (\bm{h}_j + \bm{e}_j)$ $c_{i}^{l} = \sum_{j} a_{ij}^{l} (h_{j} + e_{j})$ 。这个 $c_i^l$ $c_{i}^{l}$ 会与该层的卷积输出 $\bm{z}_i^l$ $z_{i}^{l}$ 结合（如相加），作为下一层的输入或最终输出的一部分。
  - 「多步」体现在：层级上（每层都关注源端）和时间步上（计算当前词注意力时，可能利用了之前词的注意力信息）。
优缺点：
- 优点：并行计算效率高。
- 缺点：捕捉非常长距离的依赖关系可能不如 RNN 或 Transformer 直接。

自注意力神经网络翻译模型（Transformer）

Transformer 模型是 NMT 乃至整个 NLP 领域的里程碑式工作，它完全摒弃了 RNN 和 CNN，仅依赖自注意力机制来处理序列依赖关系。

动机：实现最大程度的并行计算，并更有效地捕捉长距离依赖。
核心：自注意力（Self-Attention）机制。

整体架构

Transformer 遵循 Encoder-Decoder 架构，但其内部由 N 个相同的 Transformer Block 堆叠而成（原论文中 N=6）。

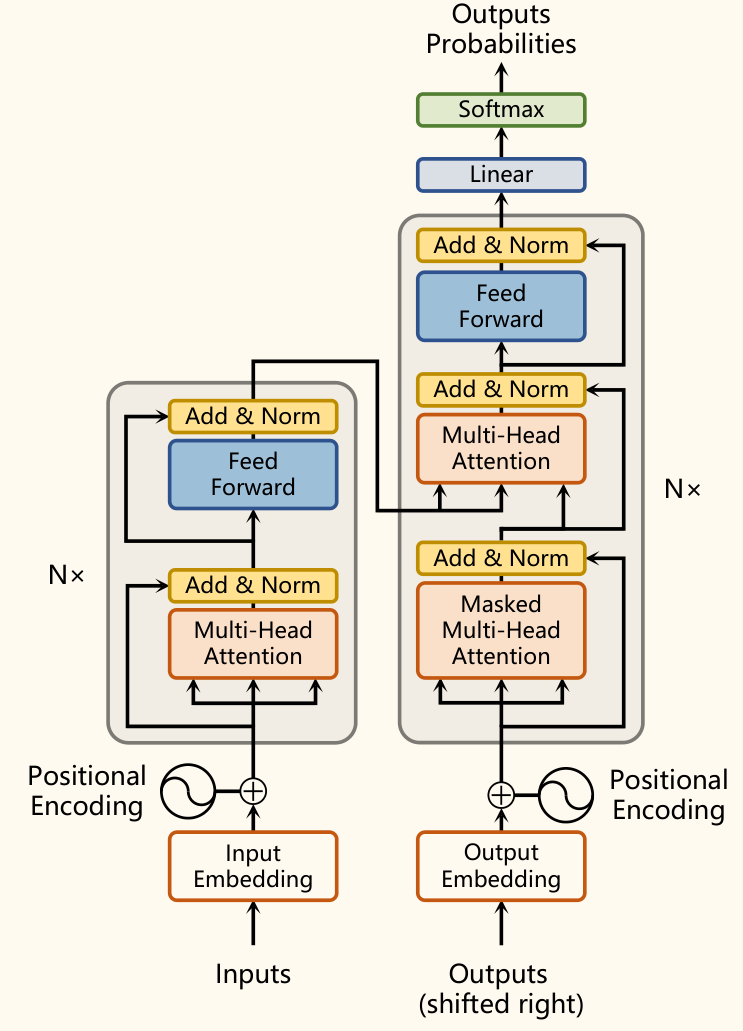
每个 Transformer Block 包含：
- 多头自注意力（Multi-Head Self-Attention）子层：计算输入序列内部的依赖关系。
- 位置前馈网络（Position-wise Feed-Forward Network）子层：一个简单的两层全连接网络，独立应用于每个位置。
- 残差连接（Add）和 层标准化（Norm）：每个子层之后都应用 Add & Norm 操作。output = LayerNorm(x + Sublayer(x))。

关键组件详解

自注意力
- 目的：计算一个序列内部，每个词对于其他所有词（包括自身）的依赖程度或相关性。
- 机制：对输入序列中的每个词的嵌入 $x_i$ $x_{i}$ ，通过乘以不同的权重矩阵 $\bm{W}^Q, \bm{W}^K, \bm{W}^V$ $W^{Q}, W^{K}, W^{V}$ ，生成三个向量：
  - 查询（Query） $\bm{q}_i = \bm{x}_i \bm{W}^Q$
  - 键（Key） $\bm{k}_i = \bm{x}_i \bm{W}^K$
  - 值（Value） $\bm{v}_i = \bm{x}_i \bm{W}^V$
- 计算过程：
  a. 计算得分：查询 $\bm{q}_i$ 与所有键 $\bm{k}_j$ 进行点积，衡量 $i$ 和 $j$ 的相关性。然后进行缩放（除以 $\sqrt{d_k}$ ， $d_k$ 是键向量的维度）以稳定梯度。
  $$
  \operatorname{score}(\bm{q}_i, \bm{k}_j) = \frac{\bm{q}_i \cdot \bm{k}j^\intercal}{\sqrt{d_k}}
  $$
  b. 计算权重：对得分应用 Softmax 函数，得到注意力权重 $\alpha_{ij}$ 。
  $$
  \alpha{ij} = \operatorname{Softmax}_j(\operatorname{score}(\bm{q}_i, \bm{k}_j))
  $$
  c. 计算输出：将所有值向量 $\bm{v}_j$ 根据注意力权重 $\alpha_{ij}$ 加权求和，得到该位置 $i$ 的自注意力输出 $\bm{z}_i$ 。
  $$
  \bm{z}i = \sum_j \alpha{ij} \bm{v}_j
  $$
- 矩阵形式：对于整个序列的嵌入矩阵 $X$ ，可以高效地并行计算：
  $\operatorname{Attention}(\bm{Q}, \bm{K}, \bm{V}) = \operatorname{Softmax}\left(\frac{\bm{Q}\bm{K}^\intercal}{\sqrt{d_k}}\right)\bm{V}$
  其中 $\bm{Q}=\bm{X}\bm{W}^Q, \bm{K}=\bm{X}\bm{W}^K, \bm{V}=\bm{X}\bm{W}^V$ 。
多头注意力
- 动机：让模型能够同时关注来自不同表示子空间的信息。单一自注意力可能只关注一种依赖模式。
- 机制：
  a. 将 $\bm{Q}, \bm{K}, \bm{V}$ 通过不同的线性变换（乘以 $\bm{W}^Q_h, \bm{W}^K_h, \bm{W}^V_h$ ）投影到 $h$ 个不同的低维子空间（ $h$ 是头的数量）。
  b. 在每个子空间上并行计算自注意力，得到 $h$ 个输出 $\text{head}_h = \operatorname{Attention}(\bm{Q}\bm{W}^Q_h, \bm{K}\bm{W}^K_h, \bm{V}\bm{W}^V_h)$ 。
  c. 将这 $h$ 个输出拼接起来。
  d. 再通过一个最终的线性变换（乘以 $\bm{W}^O$ ）得到多头注意力的最终输出。
  $\operatorname{MultiHead}(\bm{Q}, \bm{K}, \bm{V}) = \operatorname{Concat}(\text{head}_1, \dots , \text{head}_h)\bm{W}^O$
- 优点：增强了模型捕捉不同类型依赖关系的能力。
位置编码
- 目的：由于 Transformer 没有循环或卷积结构，本身无法感知词的顺序，需要显式注入位置信息。
- 方法：使用不同频率的正弦和余弦函数生成固定（非学习）的位置编码向量 $\text{PE}$ ，其维度与词嵌入相同。将其加到词嵌入上。
  $\text{PE}_{(\text{pos}, 2i)} = \sin(\text{pos}/10000^{2i/d_{\text{model}}})$
  
  $\text{PE}_{(\text{pos}, 2i+1)} = \cos(\text{pos}/10000^{2i/d_{\text{model}}})$
  其中 $\text{pos}$ 是词的位置， $i$ 是编码向量的维度索引， $d_{\text{model}}$ 是嵌入维度。这种编码方式使得模型能学习到相对位置信息。
前馈子层
- 结构：一个两层的全连接网络，中间使用 ReLU 激活函数。独立地作用于序列中的每个位置。
  $\operatorname{FFN}(\bm{x}) = \max(0, \bm{x}\bm{W}_1 + \bm{b}_1)\bm{W}_2 + \bm{b}_2$
- 作用：对自注意力层的输出进行非线性变换，增加模型深度和表达能力。通常 FFN 的中间层维度（如 2048）远大于自注意力层维度（如 512）。
残差连接与层标准化
- 残差连接：将每个子层（自注意力或 FFN）的输入 $\bm{x}$ 直接加到其输出 $\operatorname{Sublayer}(\bm{x})$ 上。 $\bm{x} + \operatorname{Sublayer}(\bm{x})$ 。有助于避免梯度消失，使深度网络更容易训练。
- 层标准化：在残差连接之后应用。对每个样本的层内所有神经元的输出进行标准化（使其均值为 0，方差为 1），然后再进行缩放和平移（使用可学习参数 $g, b$ ）。 $\operatorname{LN}(\bm{x}) = g \frac{\bm{x} - \mu}{\sqrt{\sigma^2 + \epsilon}} + b$ 。有助于稳定训练过程，加速收敛。

解码器特殊设计

解码器结构与编码器类似，但有两处关键不同：

掩码多头自注意力：解码器在生成第 $i$ 个词时，只能依赖于前面已经生成的 $i-1$ 个词，不能看到未来的词。因此，在解码器的第一个自注意力子层中，需要使用一个掩码将当前位置之后的所有位置的注意力得分设置为负无穷（或一个非常小的负数），这样 Softmax 之后这些位置的权重就接近于 0。
编码器-解码器注意力：解码器的第二个注意力子层，其 Query 来自于解码器上一层的输出，而 Key 和 Value 则来自于编码器的最终输出。这使得解码器能够关注源语言句子的相关部分，将源语信息融入目标语生成过程。

Transformer 总结

优点：
- 高度并行化，训练速度快。
- 通过自注意力直接连接任意两个位置，有效捕捉长距离依赖。
- 成为 NMT 乃至众多 NLP 任务的 SOTA 模型基础。
缺点：
- 计算复杂度与序列长度的平方相关（自注意力部分），处理超长序列时开销大。
- 对位置信息的编码不如 RNN 直观。