神经网络基础

多层感知机

M-P 神经元模型

可参考《机器学习》「神经网络」笔记。

M-P 神经元模型是模拟生物神经元工作机制的简化数学模型。它接收来自其他神经元的输入 $x_i$，每个输入都乘以对应的连接权重 $w_i$。所有加权输入求和后，减去一个阈值 $\theta$，最后通过一个激活函数 $f$ 得到输出 $y$。

$$y = f\left(\sum_{i=1}^{n} w_ix_i - \theta\right)$$

感知机模型

更规范的感知机模型可以表示为：

$$y = \begin{cases} 1, & \text{if } \sum_{i} w_ix_i + b \ge 0 \\ 0, & \text{else} \end{cases}$$

其中 $b = -\theta$ 为偏置。

激活函数

理想的激活函数是阶跃函数（sgn），$0$ 表示抑制神经元，$1$ 表示激活神经元。但阶跃函数不连续、不光滑，实际应用中常用的是Sigmoid 函数。

阶跃函数与 Sigmoid 函数

阶跃函数：
$\operatorname{sgn}(x) = \begin{cases} 1, & \text{if } x > 0 \\ 0, & \text{if } x \le 0 \end{cases}$

Sigmoid 函数：
$\operatorname{sigmoid}(x) = \frac{1}{1 + \e^{-x}}$

Logistic 回归模型

线性回归（Linear Regression）

$$y = \sum_{i} w_ix_i + b$$

Logistic 回归（Logistic Regression）：处理二元分类问题，$y$ 为输出的概率。

• 例如：垃圾邮件过滤、褒贬识别。

Logistic 函数

$$y = \frac{1}{1 + \e^{-k(z-z_0)}}$$

其中 $z = \sum_{i} w_ix_i + b$。

标准 Logistic 函数（Sigmoid 型函数）：

$$y = \frac{1}{1 + \e^{-z}}$$

Softmax 回归

Softmax 回归用于处理多元分类问题。

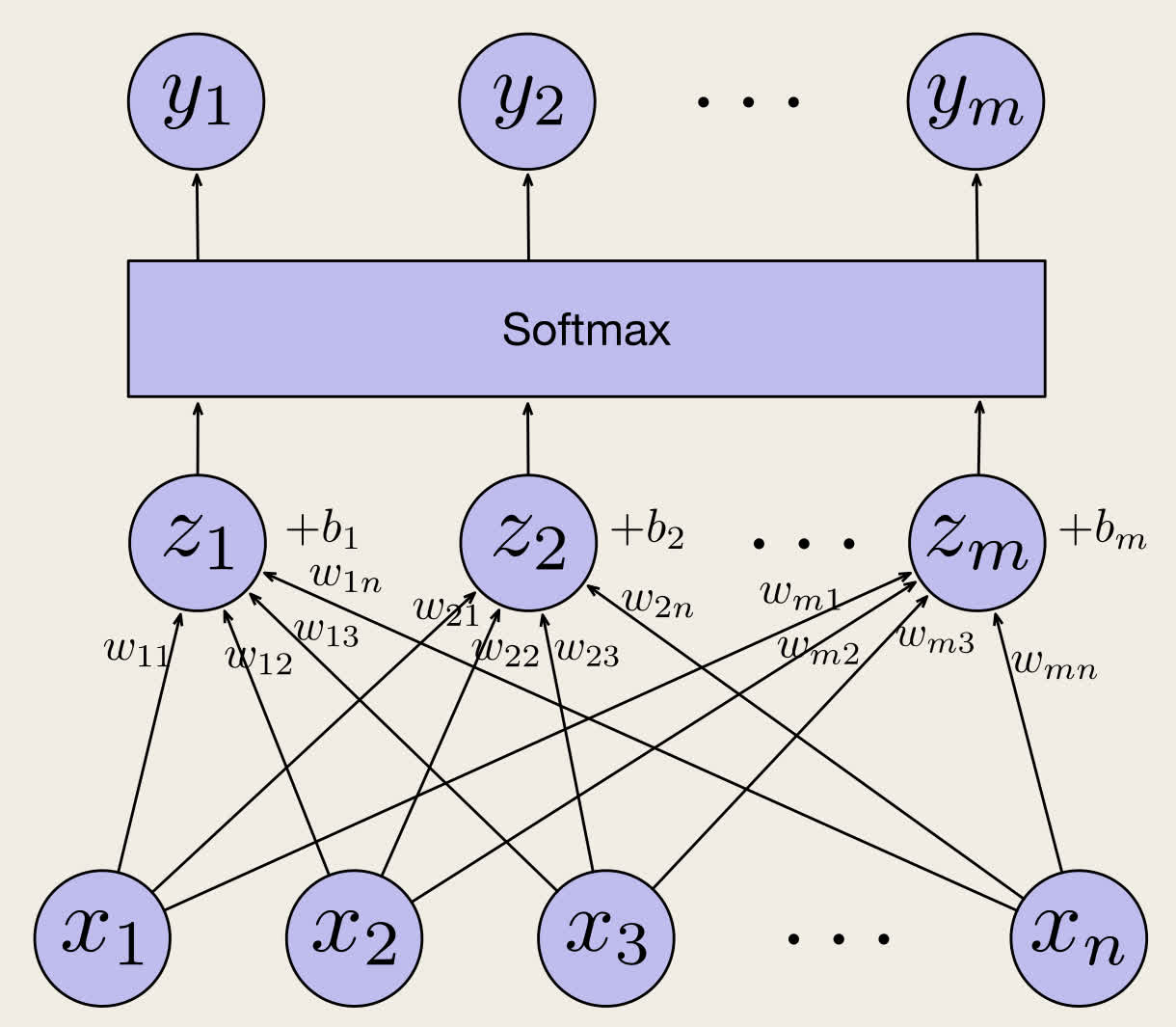
Softmax 函数：

$$y_i = \operatorname{Softmax}(\bm{z})_i = \frac{\e^{z_i}}{\sum_{j} \e^{z_j}}$$

其中

• $y_i$ 为第 $i$ 个类别的概率
• $z_i = \sum_{j} w_{ij}x_k + b$
• $w_{ij}$ 为第 $i$ 个类别所对应的第 $j$ 个输入的权重。

Logistic 回归是 Softmax 回归的特例，当类别数为 2 时，Softmax 回归退化为 Logistic 回归。

对 $\bm{y}$ 有：

$$\begin{aligned} \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_m \end{bmatrix} &= \operatorname{Softmax} \left( \begin{bmatrix} z_1 \\ z_2 \\ \vdots \\ z_m \end{bmatrix} \right) \\ &= \operatorname{Softmax} \left( \begin{matrix} w_{11} x_1 + w_{12} x_2 + \cdots + w_{1n} x_n + b_1 \\ w_{21} x_1 + w_{22} x_2 + \cdots + w_{2n} x_n + b_2 \\ \vdots \\ w_{m1} x_1 + w_{m2} x_2 + \cdots + w_{mn} x_n + b_m \end{matrix} \right)\\ &= \operatorname{Softmax} \left( \begin{bmatrix} w_{11}, w_{12}, \dots, w_{1n} \\ w_{21}, w_{22}, \dots, w_{2n} \\ \vdots \\ w_{m1}, w_{m2}, \dots, w_{mn} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} + \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{bmatrix} \right) \end{aligned}$$

即

$$\boxed{\bm{y} = \operatorname{Softmax}(\bm{W} \bm{x} + \bm{b})}$$

多层感知机

多层感知机（MLP）由多层感知机单元（线性回归 + 非线性激活函数）堆叠而成，可以解决线性不可分问题，例如异或问题（XOR）。

常用激活函数

激活函数	函数	导数
Logistic 函数	$f(x) = \frac{1}{1 + \exp(-x)}$	$f'(x) = f(x)(1 - f(x))$
Tanh 函数	$f(x) = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)}$	$f'(x) = 1 - f(x)^2$
ReLU 函数	$f(x) = \max(0, x)$	$f'(x) = \mathbb{I}(x > 0)$
ELU 函数	$f(x) = \begin{cases} x, & x>0 \\ \gamma(\e^x - 1), & x \le 0 \end{cases}$	$f'(x) = \begin{cases} 1, & x>0 \\ \gamma \e^x, & x \le 0 \end{cases}$
SoftPlus 函数	$f(x) = \log(1 + \exp(x))$	$f'(x) = \frac{1}{1 + \exp(-x)}$

Tanh 函数

Tanh 函数也是一种 Sigmoid 型函数，其值域是 $(-1, 1)$。

$\tanh(x) = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)} = 2\sigma(2x) - 1$

Hard-Logistic/Tanh 函数

Logistic 函数和 Tanh 函数都是 Sigmoid 型函数，在中间（0 附近） 近似线性，两端饱和，计算开销较大，可以用分段函数来近似：

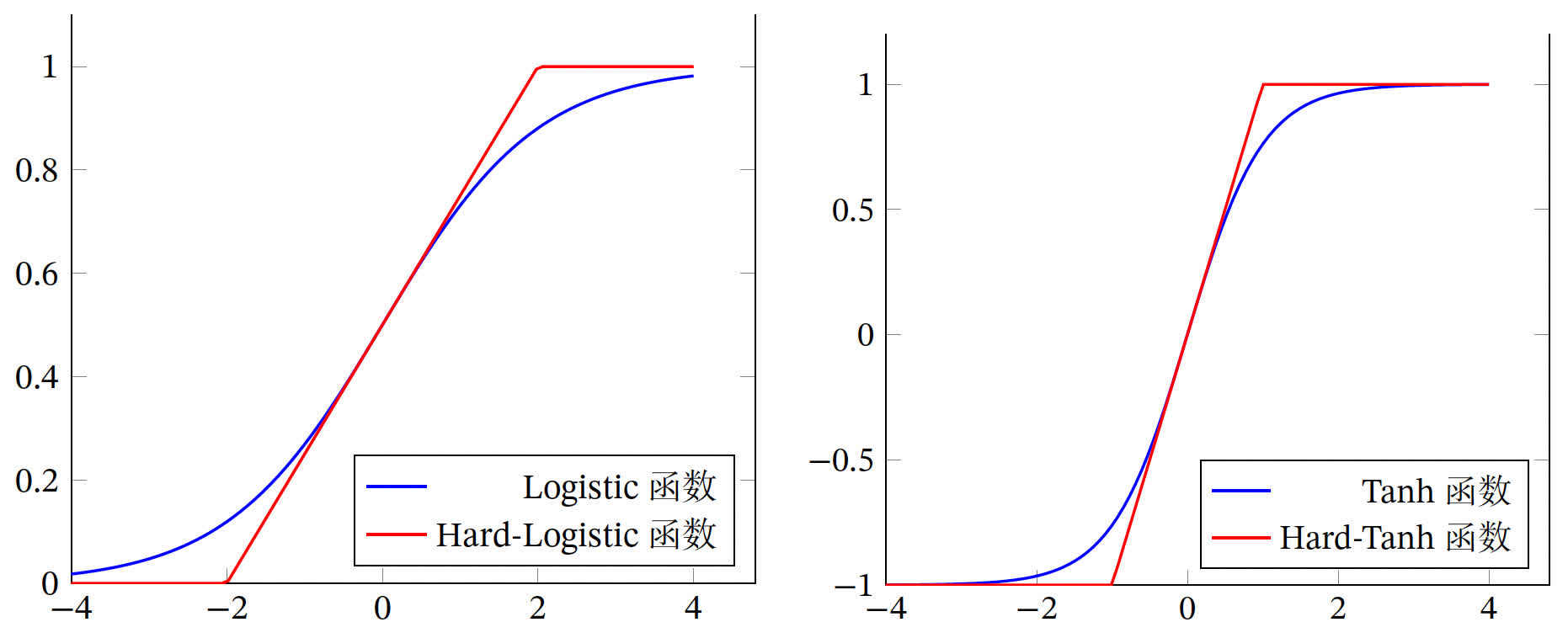
ReLU 函数

ReLU（Rectified Linear Unit，修正线性单元）是目前深度神经网络中经常使用的激活函数。

$$\operatorname{ReLU}(x) = \max(0, x)$$

ReLU 函数的优缺点

• 优点：计算高效；一定程度上缓解梯度消失问题，加速梯度下降收敛速度。
• 缺点：容易「死亡」，如果参数在一次不恰当的更新后，某个神经元在所有的训练数据上都不能被激活，那么其自身参数梯度永远会是 0，在以后的训练过程中永远不能被激活。

ReLU 函数变体

Leaky ReLU 函数：

$$\operatorname{LeakyReLU}(x) = \max(0, x) + \gamma \min(0, x)$$

ELU 函数：

$$\operatorname{ELU}(x) = \begin{cases} x, & x > 0 \\ \gamma(\exp(x) - 1), & x \le 0 \end{cases}$$

SoftPlus 函数：

$$\operatorname{SoftPlus}(x) = \log(1 + \exp(x))$$

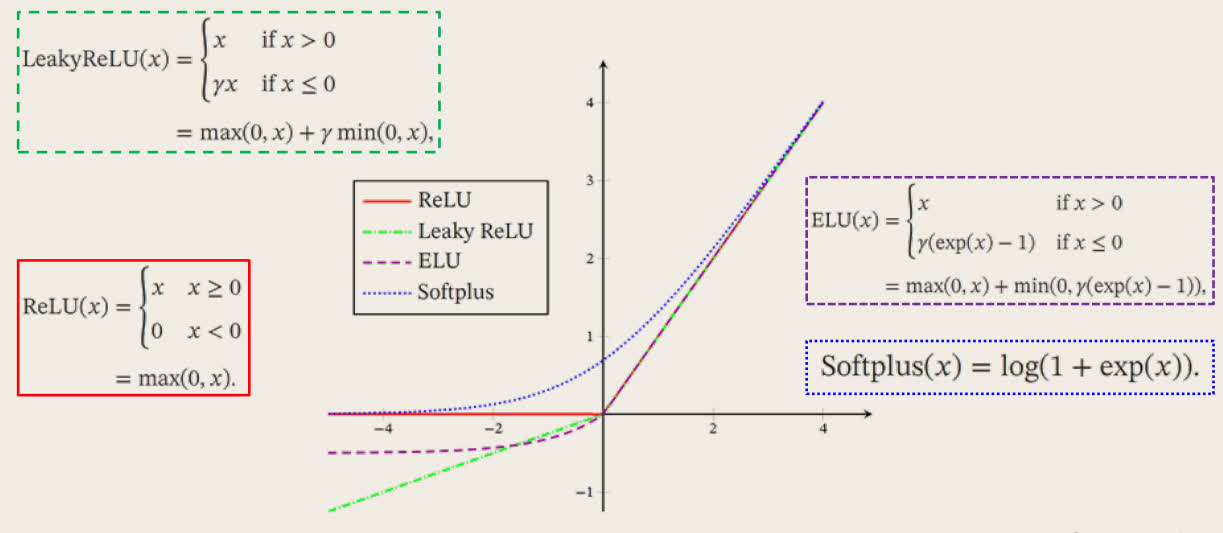
卷积神经网络

可以去下面两个网址玩玩：

• A Neural Network Playground
• CNN Explainer

全连接的多层感知机局限性：无法处理输入的偏移情况，例如图像分类和情感分类中，输入的微小偏移会导致输出的巨大变化。

全连接

全连接是指网络中的每个神经元都与上一层的所有神经元相连。

解决方案：卷积神经网络（Convolutional Neural Network, CNN）

• 使用小的全连接层抽取局部特征（又称卷积核或滤波器），例如遍历文本中的 N-gram。
• 使用多个卷积核提取不同种类的特征。
• 使用池化层（Pooling, 聚合层）将特征进行聚合（最大、平均、求和等）。

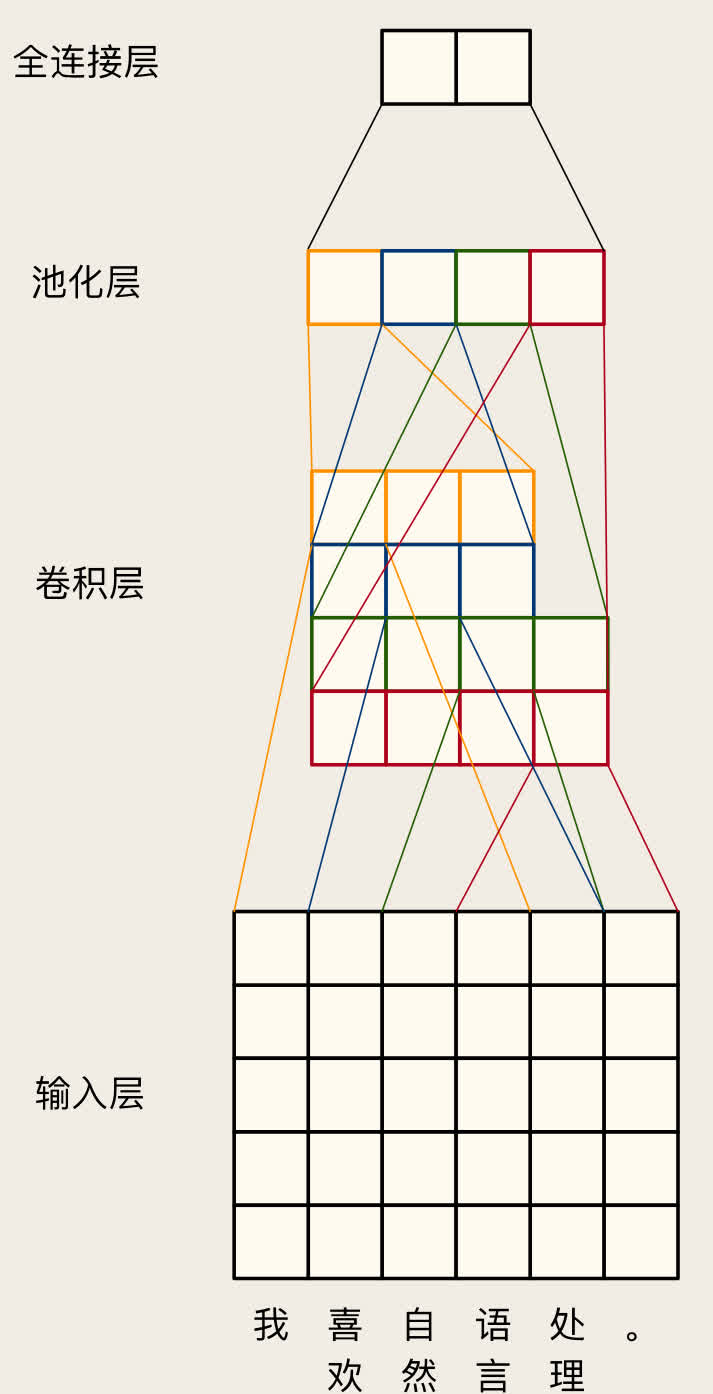
2D-卷积层：

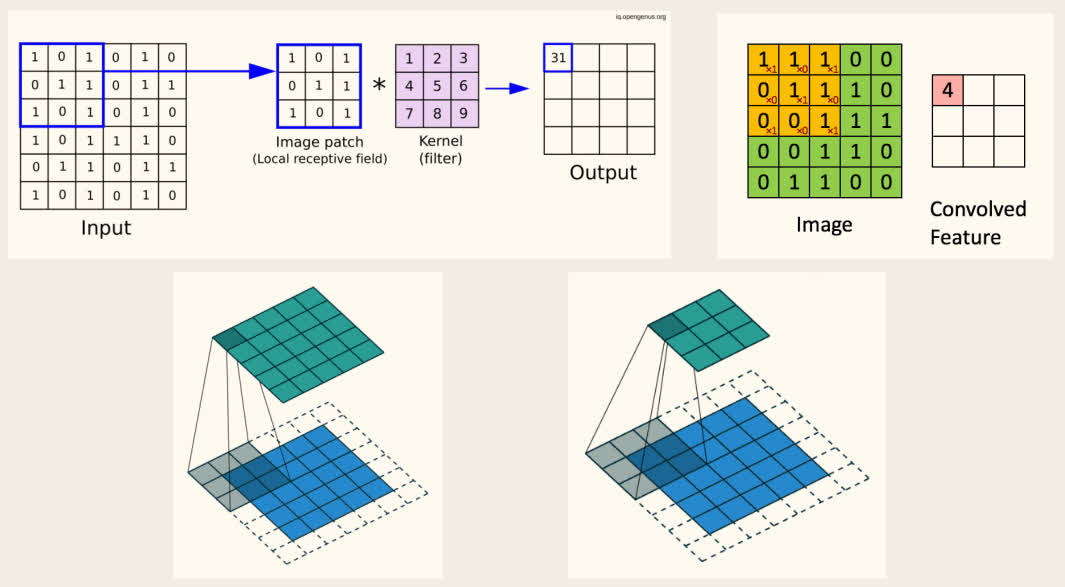
3D-卷积层：

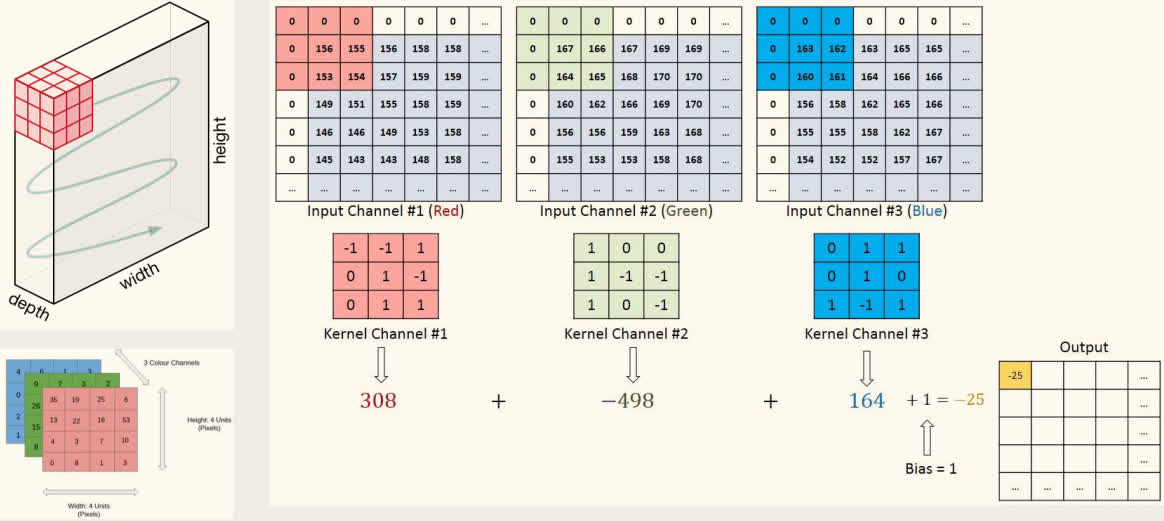
卷积层 vs. 全连接层：

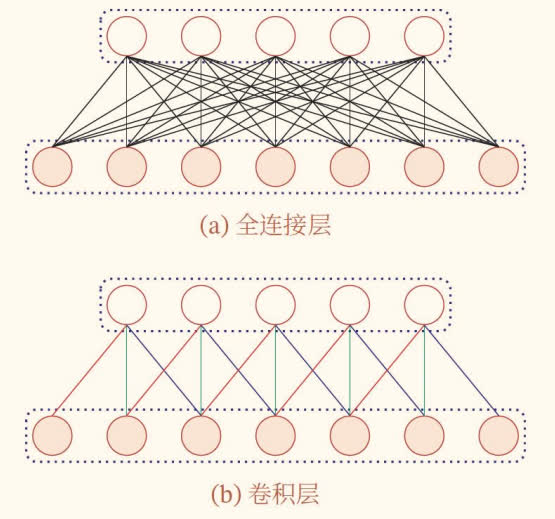
循环神经网络

卷积神经网络无法处理长距离的依赖关系。

循环神经网络（Recurrent Neural Network, RNN）通过隐状态来存储历史信息，每个时刻的隐状态依赖于当前时刻的输入以及上一时刻的隐状态。

$$\begin{aligned} \bm{h}_t &= \tanh(\bm{W}^{\text{xh}}\bm{x}_t + \bm{b}^{\text{xh}} + \bm{W}^{\text{hh}}\bm{h}_{t-1} + \bm{b}^{\text{hh}}) \bm{y} &= \operatorname{Softmax}(\bm{W}^{\text{hy}}\bm{h}_n + \bm{b}^{\text{hy}}) \end{aligned}$$

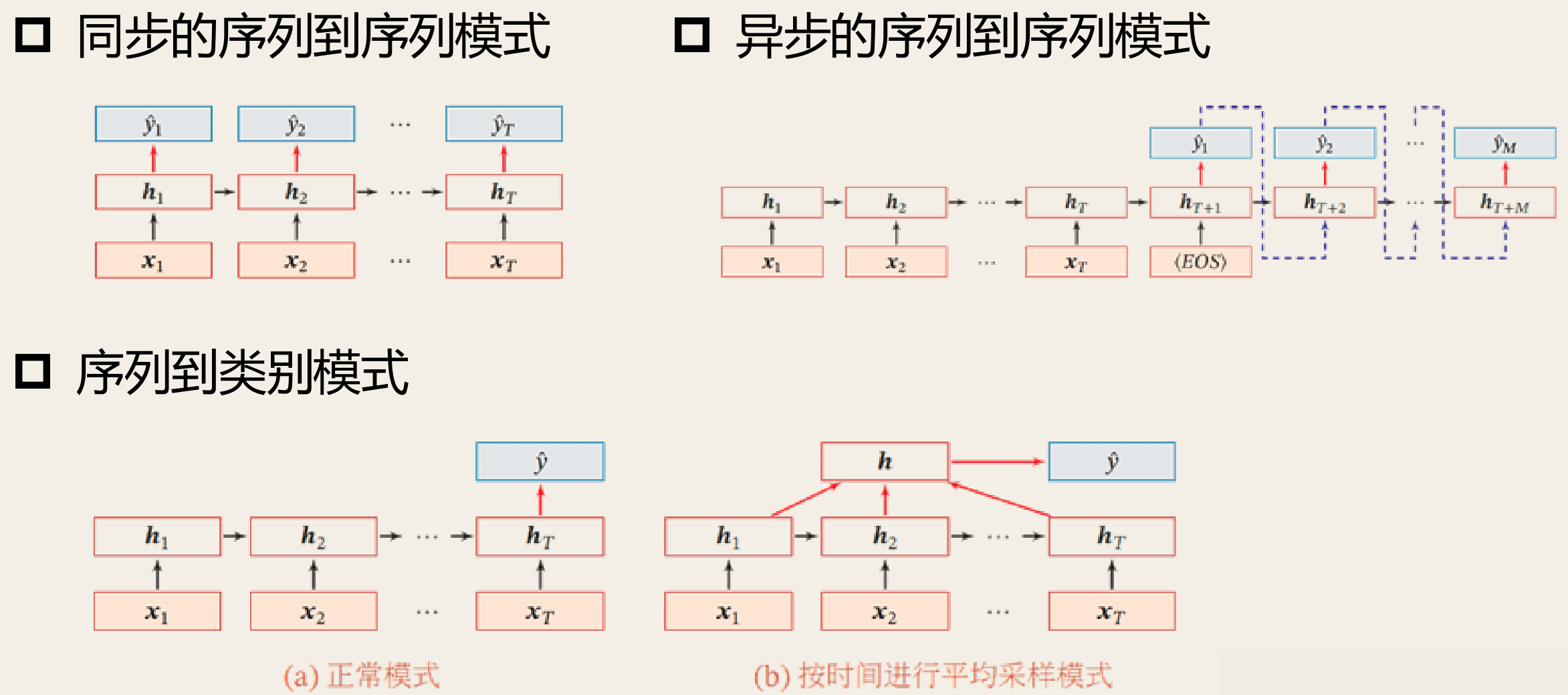
每个时刻的参数共享（循环），每个时刻也可以有相应的输出（序列标注）。

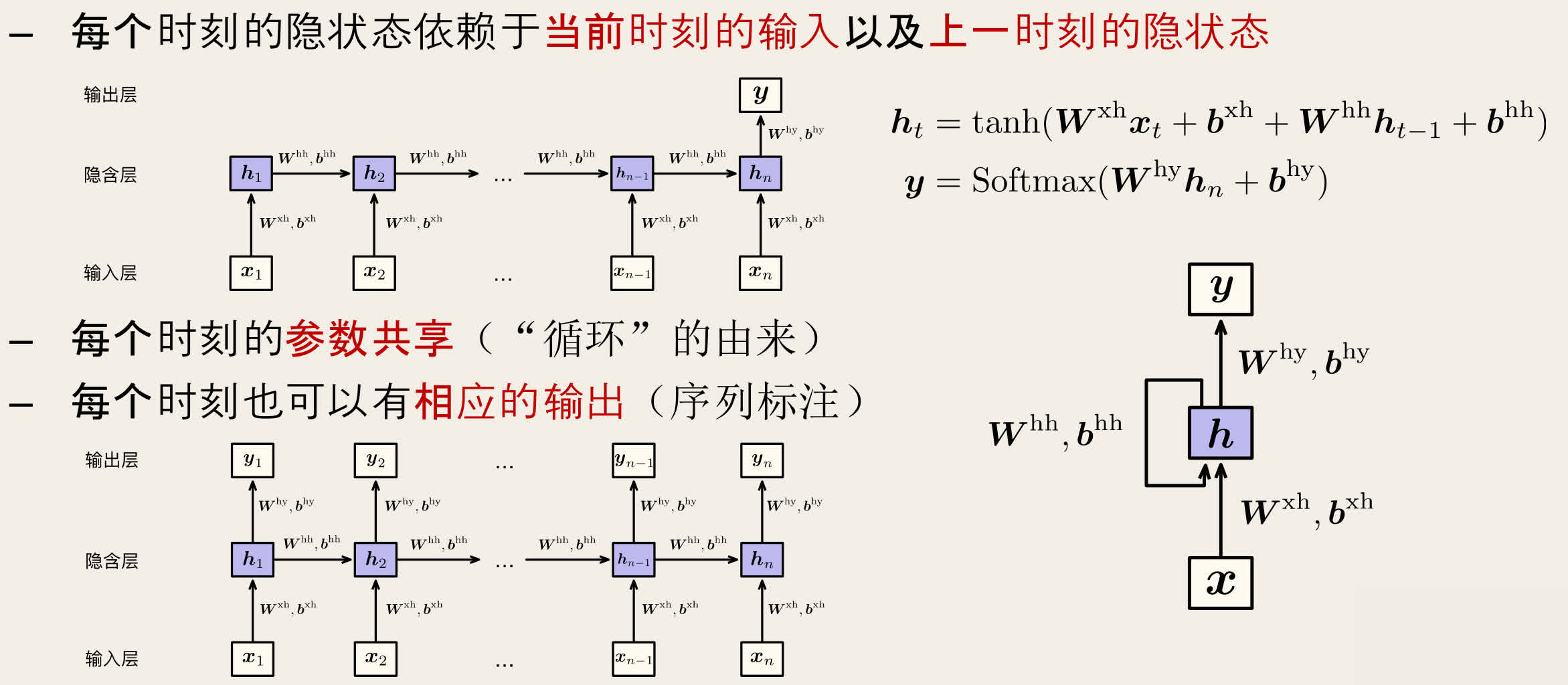
RNN 的参数在每个时刻共享，每个时刻也可以有相应的输出（序列标注）。

长短时记忆网络（LSTM）

梯度消失与爆炸

序列过长时，原始的 RNN 容易导致梯度消失或梯度爆炸，从而丢失信息。

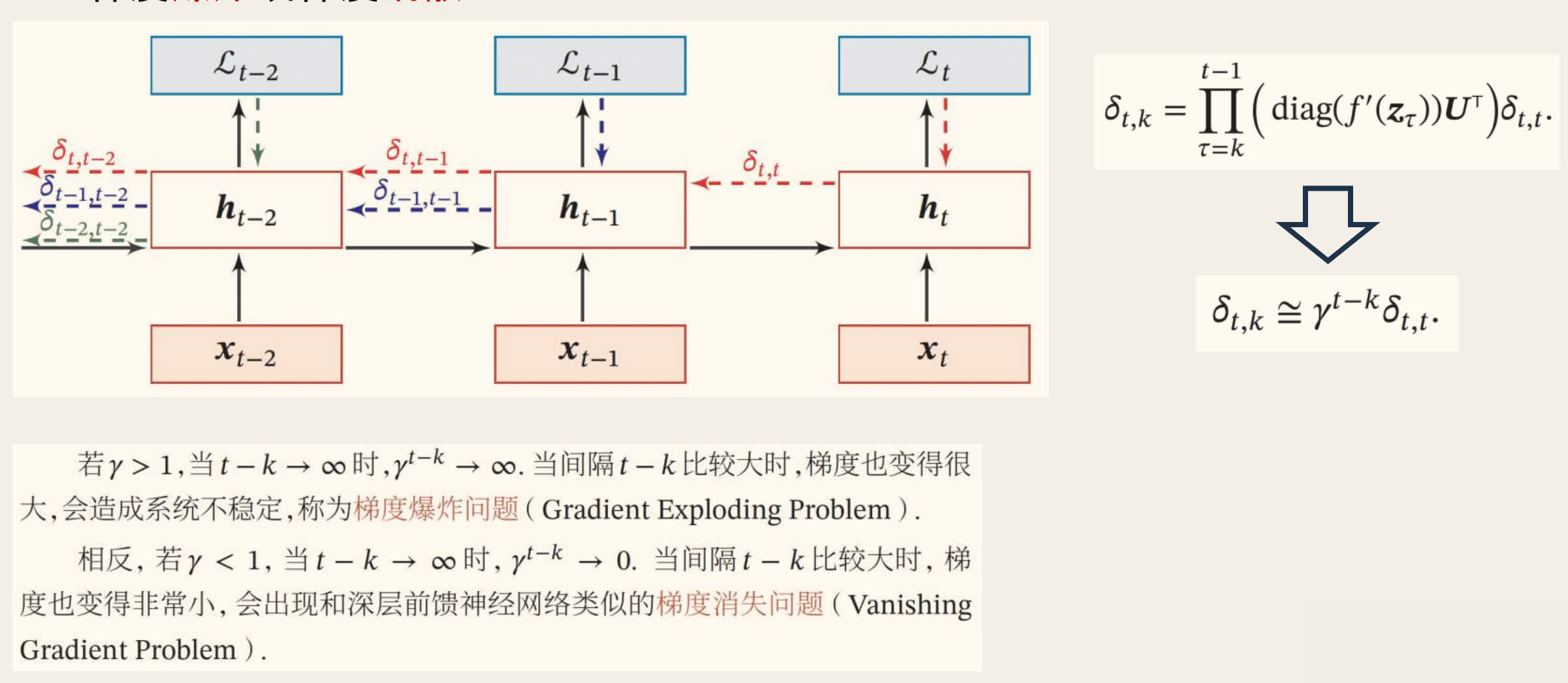
LSTM 的改进

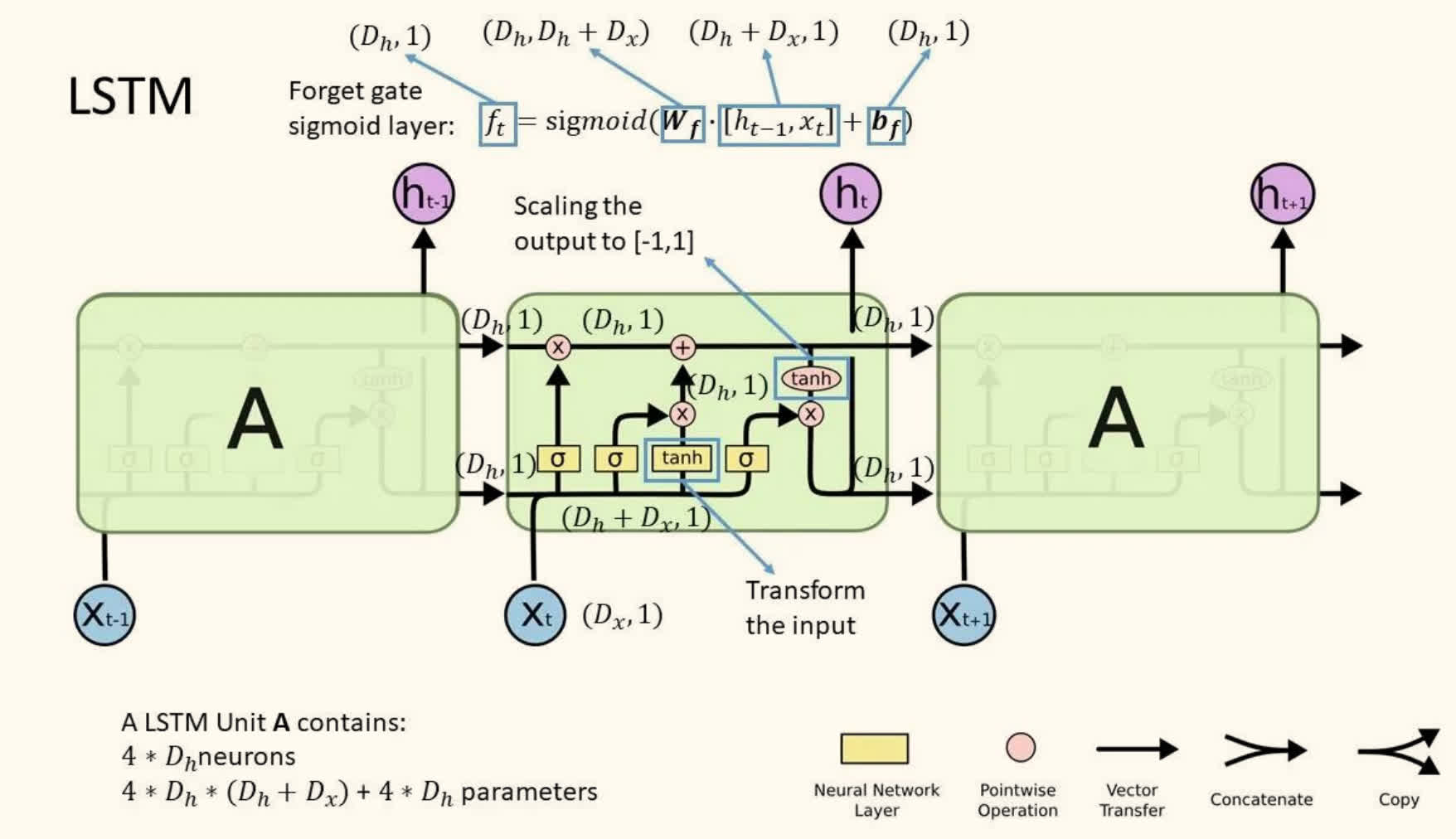
LSTM 通过引入门控机制来控制信息的流动，包括遗忘门、输入门和输出门。

新的加性隐状态更新方式：

$$\begin{aligned} \bm{u}_t &= \tanh\left( \bm{W}^{\text{xh}} \bm{x}_t + \bm{b}^{\text{xh}} + \bm{W}^{\text{hh}} \bm{h}_{t - 1} + \bm{b}^{\text{hh}} \right) \\ \bm{h}_t &= \bm{h}_{t-1} + \bm{u}_t \end{aligned}$$

其中：

• $\bm{h}_{t-1}$ 是长期记忆（long-term memory）
• $\bm{u}_t$ 是短期记忆（short-term memory）

相当于直接将 $\bm{h}_{k}$ 与 $\bm{h}_t\, (k < t)$进行了跨层连接：

$$\begin{aligned} \bm{h}_t &= \bm{h}_{t-1} + \bm{u}_t\\ &= \bm{h}_{t-2} + \bm{u}_{t-1} + \bm{u}_t\\ &= \bm{h}_{k} + \sum_{i=k+1}^{t} \bm{u}_i \end{aligned}$$

进一步改进：

• 遗忘门（Forget Gate）：控制遗忘信息，考虑旧状态 $\bm{h}_{t-1}$ 和新状态 $\bm{u}_{t}$ 的贡献
• 输入门（Input Gate）：控制输入信息，独立控制 $\bm{h}_{t-1}$ 和 $\bm{u}_t$ 的贡献
• 输出门（Output Gate）：控制输出信息

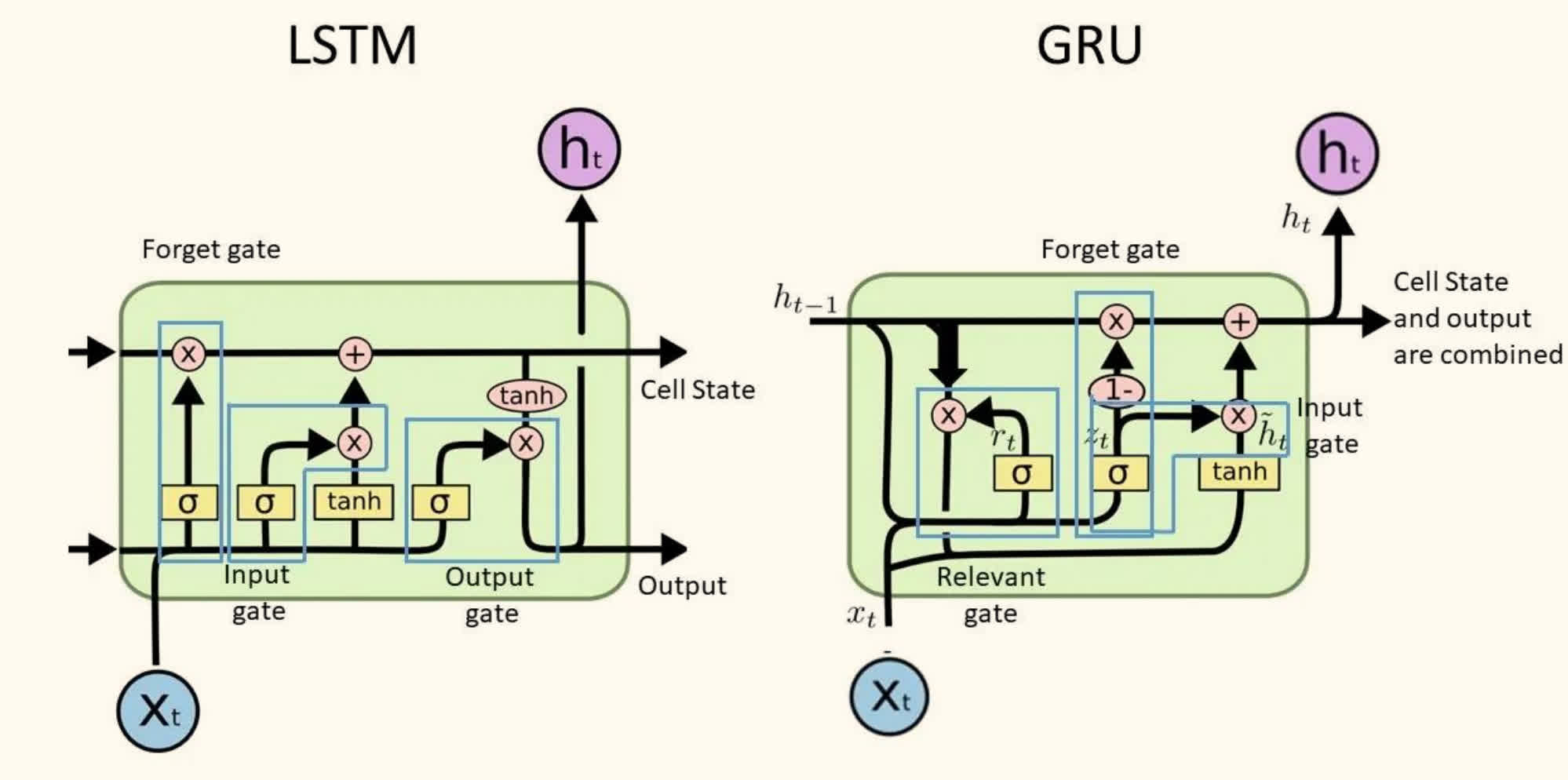
GRU 是 LSTM 的一种简化版本，它将细胞状态和隐状态合并，并使用更新门和重置门来控制信息的流动。

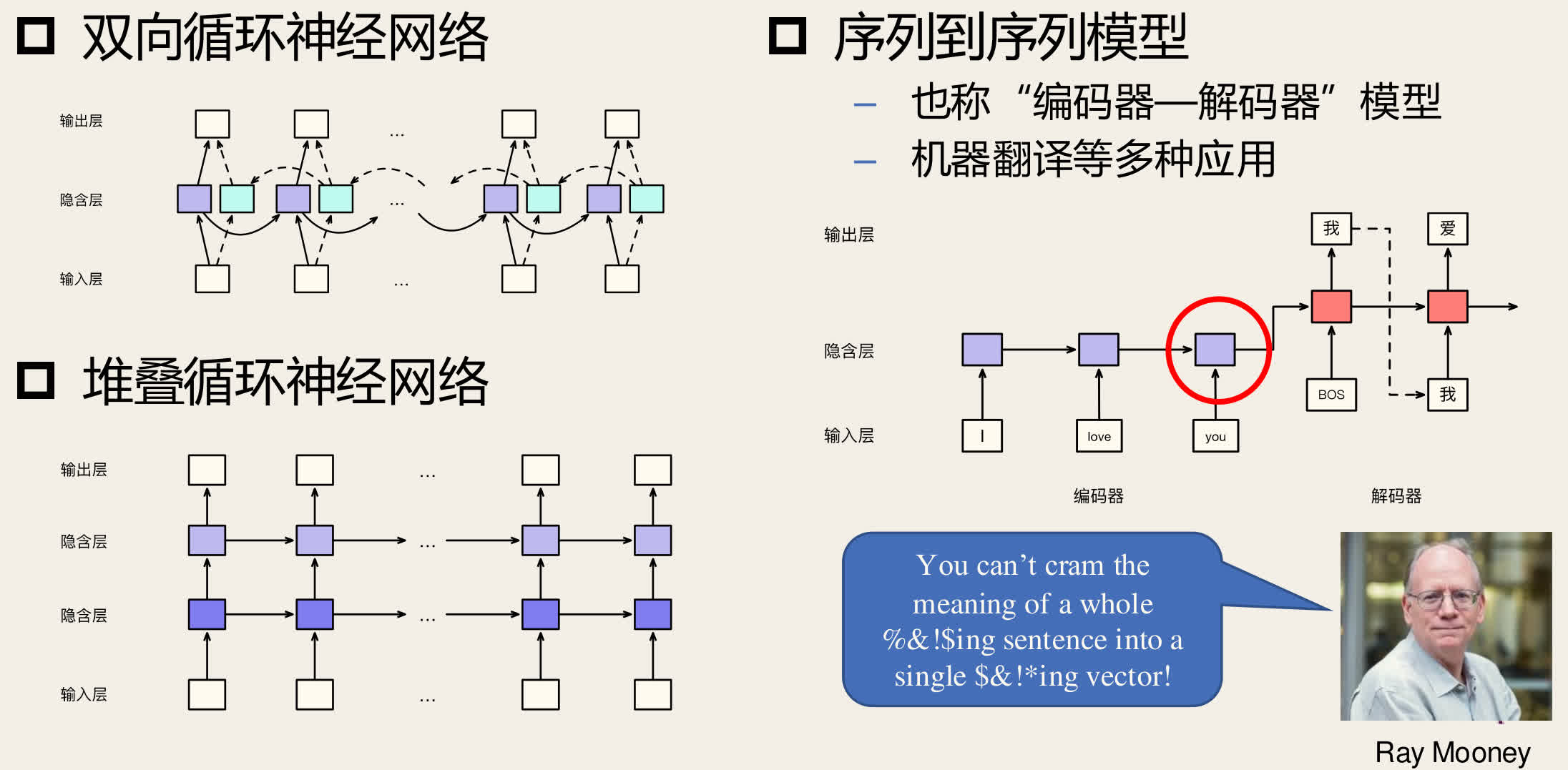
循环神经网络的应用

• 双向循环神经网络
• 序列到序列模型（编码器-解码器模型），例如机器翻译
• 堆叠循环神经网络

Transformer

注意力机制

注意力一般分为两种：

• 聚焦式注意力（Focus Attention）：自上而下的有意识的注意力。
  • 有预定目的、依赖任务的，主动有意识地聚焦于某一对象的注意力。
• 显著性注意力（Saliency-Based Attention）：自下而上的无意识的注意力。
  • 由外界刺激驱动的注意，不需要主动干预，也和任务无关。

一个和注意力有关的例子是「鸡尾酒效应」。

当一个人在吵闹的鸡尾酒会上和朋友聊天时，尽管周围噪音干扰很多，他还是可以听到朋友的谈话内容，而忽略其他人的声音（聚焦式注意力）。

同时，如果背景声中有重要的词（比如他的名字），他会马上注意到（显著性注意力）。

当前状态除和前一个状态及输入相关外，还应关注原序列的状态。

注意力机制的核心思想是根据当前状态和输入，对原序列的状态进行加权求和。

打分公式：

$$\begin{aligned} \hat{\alpha}_s &= \text{attn}(\bm{h}_s, \bm{h}_{t-1})\\ \alpha_s &= \operatorname{Softmax}(\hat{\bm{\alpha}})\\ \operatorname{attn}(\bm{q}, \bm{k}) &= \begin{cases} \bm{w}^\intercal \tanh(\bm{W}[\bm{q}; \bm{k}]) & \text{（点积注意力）}\\ \bm{q}^\intercal \bm{W} \bm{k} & \text{（缩放点积注意力）}\\ \bm{q}^\intercal \bm{k} & \text{（加性注意力）}\\ \dfrac{\bm{q}^\intercal \bm{k}}{\sqrt{d}} & \text{（缩放点积注意力）} \end{cases} \end{aligned}$$

自注意力模型

「自注意力模型」通过计算输入序列中任意两个向量之间的相关性（注意力值）来更新每个向量。

• 输入 $n$ 个向量构成的序列 $\bm{x}_1, \dots, \bm{x}_n$
• 输出每个向量对应的新向量 $\bm{y}_1, \dots, \bm{y}_n$
• $\bm{y}_i = \sum_{j=1}^{n} \alpha_{ij} \bm{x}_{j}$
  • $\alpha_{ij}$ 为 $\bm{x}_{i}, \bm{x}_{j}$ 之间的注意力值

自注意力模型还需要解决的几个问题

• 没有考虑输入的位置信息
• 输入向量 $x_i$ 同时承担三种角色，不易学习
• 计算注意力权重时的两个向量以及被加权的向量
• 只考虑了两个输入向量之间的关系，无法建模多个向量之间的更复杂关系
• 自注意力计算结果互斥，无法同时关注多个输入

融入位置信息：输入向量 = 词向量 + 位置嵌入/编码

• 位置嵌入（Positional Embedding）
  • 类似词嵌入，每个绝对位置赋予一个连续、低维、稠密的向量表示
  • 向量参数参与模型学习
• 位置编码（Positional Encoding）
  • 直接将一个整数（位置索引值）映射为一个向量

Transformer 模型向量：

• Query（查询向量）：当前关注的焦点
• Key（键向量）：其他位置的标识
• Value（值向量）：实际携带的信息

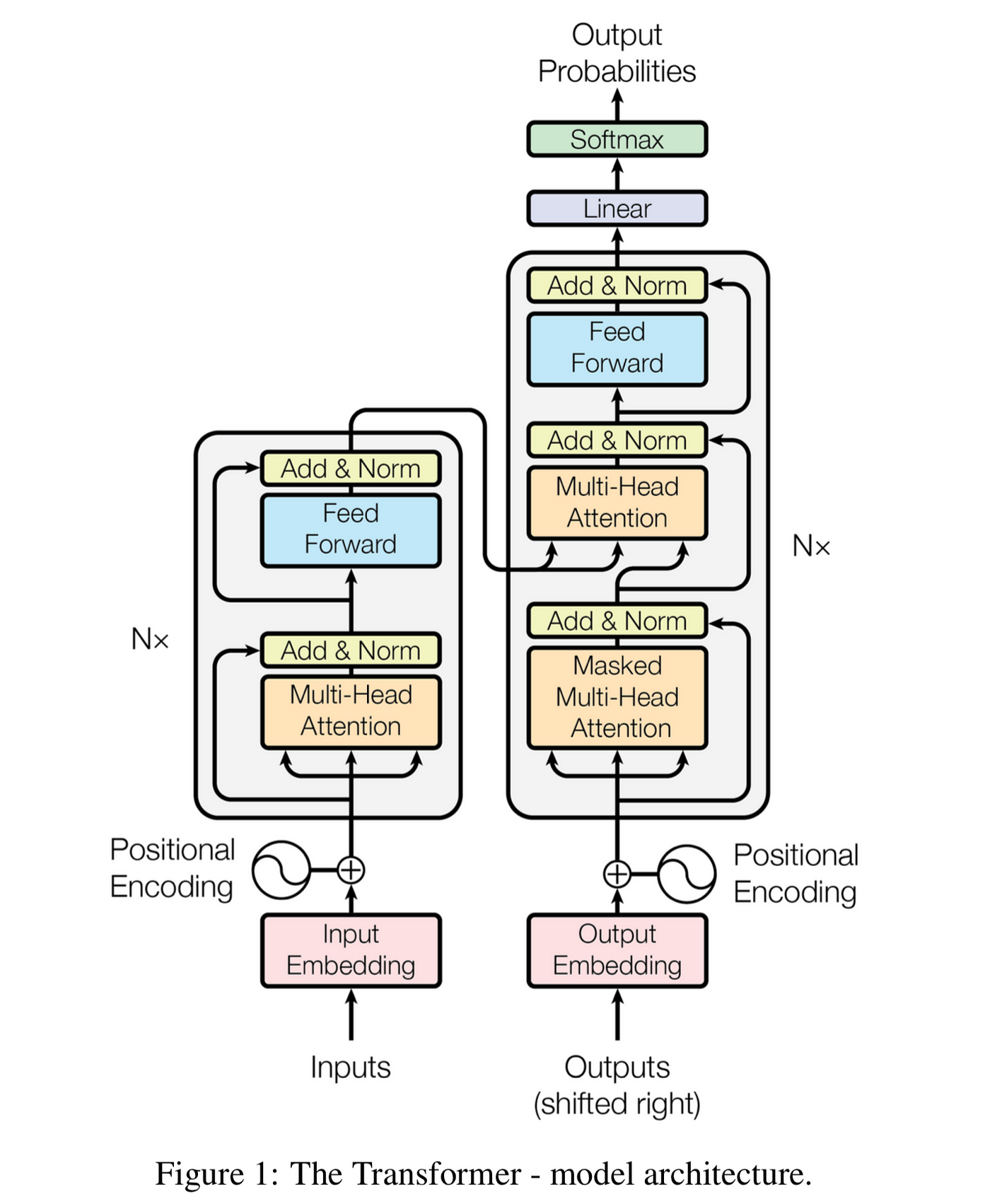
多层自注意力

原始自注意力模型仅考虑了任意两个向量之间的关系。

如何建模高阶关系？

• 直接建模高阶关系导致模型复杂度过高
• 堆叠多层自注意力模型（消息传播机制）

增强模型的表示能力——增加非线性

• 增加非线性的多层感知器模型（MLP）

使模型更容易学习

• 层归一化（Layer Normalization）
• 残差连接（Residual Connections）

多头自注意力

由于 Softmax 函数的性质，无法使得多个自注意力分数趋近于 1。

使用多组自注意力模型产生多组不同的注意力结果

• 设置多组输入映射矩阵
• 类似使用多个卷积核提取不同的特征

自注意力 & 交叉注意力

自注意力机制用于计算输入序列内部的注意力分数，而交叉注意力机制用于计算两个不同序列之间的注意力分数。

神经网络模型的训练

模型训练（学习）：神经网络模型的训练目标是寻找一组优化的模型参数。

损失函数（Loss Function）

损失函数用于评估参数好坏，常用的损失函数有均方误差（MSE）和交叉熵（CE）。

均方误差（Mean Squared Error, MSE）

$$\mathrm{MSE} = \frac{1}{m}\sum_{i=1}^{m}\left(y^{(i)} - \hat{y}^{(i)}\right)^2$$

交叉熵（Cross Entropy, CE）

$$\begin{aligned} \mathrm{CE} &= -\frac{1}{m}\sum_{i=1}^{m}\sum_{j=1}^{c}y_j^{(i)}\log \hat{y}_j^{(i)}\\ &= \dfrac{1}{m} \sum_{i=1}^{m} \log \hat{y}^{(i)}_{t} & (c = 2) \end{aligned}$$

$m$ 为样本数，$c$ 为类别数，$y$ 为真实标签，$\hat{y}$ 为预测标签。第二行为二分类的交叉熵，又称为「负对数似然损失」（Negative Log Likelihood Loss, NLL）。

梯度下降

梯度（Gradient）是以向量的形式写出的对多元函数各个参数求得的偏导数，是函数值增加最快的方向。沿着梯度相反的方向，更容易找到函数的极小值。

梯度下降算法（Gradient Descent, GD）是一种迭代优化算法，通过不断更新参数来最小化损失函数。

小批次梯度下降法（Mini-batch Gradient Descent）每次随机采样小规模的训练数据来估计梯度，提高算法的运行速度。