词法分析

发表于 更新于 Waline： 阅读次数： 本文字数： 4.2k 阅读时长 ≈ 15 分钟

词法分析的角色与任务

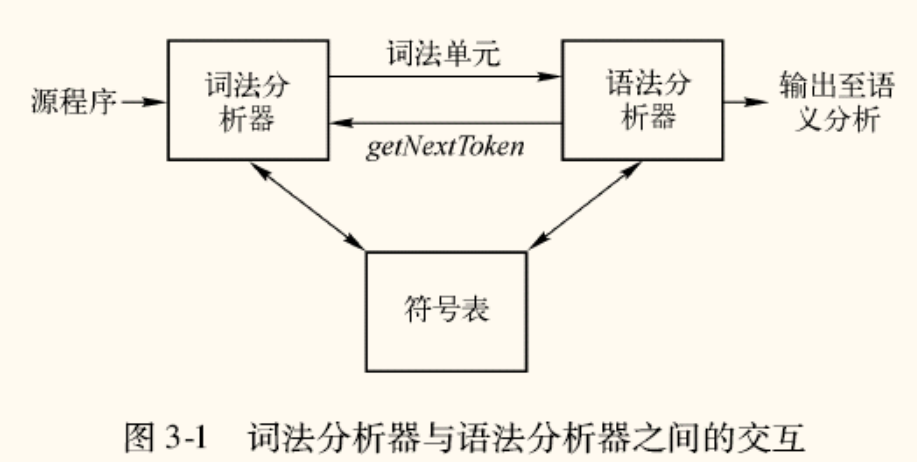
词法分析（Lexical Analysis）是编译过程的第一个阶段。它负责从左到右逐个字符地读取源程序，并将其组织成一系列有意义的记号（Token）序列。这个过程也被称为扫描（Scanning），执行词法分析的程序则称为词法分析器（Lexical Analyzer）或扫描器（Scanner）。

除了识别记号，词法分析器通常还会完成一些辅助性工作，例如：

  • 过滤掉源程序中的注释和空白（如空格、制表符、换行符）。
  • 将错误消息与源程序中的行号关联起来。

核心概念

为了理解词法分析，我们需要区分三个关键术语：记号、词素和模式。

核心概念

  • 记号（Token）：也称词法单元，是语言中具有语法意义的最小单位的类别。它通常由两部分组成：记号名（Token Name）和可选的属性值（Attribute Value）。记号名是语法分析阶段需要的信息，而属性值则为后续阶段（如语义分析、代码生成）提供附加信息。
    • 例如：<id, "position">, <number, 60>, <assign_op>。
  • 词素（Lexeme）：是指源程序中与某个模式匹配，从而被识别为一个记号实例的字符序列。
    • 例如：position 是一个词素，它匹配 id 的模式。60 是一个词素，它匹配 number 的模式。
  • 模式（Pattern）：描述一个记号的词素可能具有的形式的规则。
    • 例如，C 语言标识符的模式是「以字母或下划线开头，后跟任意数量的字母、数字或下划线」。

对于一行代码 position = initial + rate * 60;，词法分析器会将其转换为如下的记号流：

  • 源程序：position = initial + rate * 60
  • 词素序列：position, =, initial, +, rate, *, 60
  • 记号流：<id, "position">, <assign_op>, <id, "initial">, <add_op>, <id, "rate">, <mul_op>, <number, 60>

在这个例子中：

  • position 是一个词素，它对应的记号是 <id, "position">。
  • id 是记号名，"position" 是它的属性值（指向符号表中 position 条目的指针）。
  • 像 = 这样的运算符，其含义是唯一的，因此其记号 <assign_op> 可能不需要属性值。

词法单元的规约：正则表达式

我们如何精确地描述（或称规约）一个记号的模式？答案是使用正则表达式（Regular Expression, RE）。

形式语言理论基础

在介绍正则表达式之前，需要了解一些基本概念：

  • 字母表（Alphabet）：一个有限的符号集合，记作 Σ\Sigma。例如，ASCII 字符集、二进制字母表 {0, 1}。
  • 串（String）：由字母表中的符号组成的有穷序列。空串用 ε\varepsilon 表示。
    • 前缀（Prefix）：从串的尾部删除零个或多个符号得到的串。
    • 后缀（Suffix）：从串的头部删除零个或多个符号得到的串。
    • 子串（Substring）：删除串的某个前缀和某个后缀得到的串。
    • 子序列（Subsequence）：通过删除串中的某些符号（不改变剩余符号的顺序）得到的串。
  • 语言（Language）：在某个字母表 Σ\Sigma 上定义的、任意一个串的集合。例如，所有合法的 C 语言程序构成的集合就是一个语言。

语言可以进行运算：

  • 并（Union）：L∪M={s∣s∈L∨s∈M}L \cup M = \{s \mid s \in L \lor s \in M\}
  • 连接（Concatenation）：LM={st∣s∈L∧t∈M}LM = \{st \mid s \in L \land t \in M\}
  • 克林闭包（Kleene Closure）：L∗=⋃i=0∞LiL^* = \displaystyle \bigcup_{i=0}^{\infty} L^i（LL 中的串连接 0 次或多次）
  • 正闭包（Positive Closure）：L+=⋃i=1∞LiL^+ = \displaystyle \bigcup_{i=1}^{\infty} L^i（LL 中的串连接 1 次或多次）

正则表达式

正则表达式是一种用于描述正则语言（Regular Language）的强大表示方法。在词法分析中，它被用来精确定义记号的模式。

正则表达式的定义

一个正则表达式 r 定义了一个语言，记为 L(r)。其定义是递归的：

  1. 基本规则：

    • ε\varepsilon 是一个正则表达式，它表示的语言是 {ε}，即只包含空串的语言。
    • 如果 a 是字母表 Σ\Sigma 中的一个符号，那么 a 是一个正则表达式，它表示的语言是 {a}。

  2. 归纳规则：假设 r 和 s 都是正则表达式，则：

    • 选择（Union）：(r)|(s) 是一个正则表达式，表示语言 L(r) ∪ L(s)。
    • 连接（Concatenation）：(r)(s) 是一个正则表达式，表示语言 L(r)L(s)。
    • 闭包（Kleene Closure）：(r)* 是一个正则表达式，表示语言 (L(r))*，即 r 出现零次或多次。

运算优先级为：闭包 > 连接 > 选择。括号可以用来改变优先级。

正则定义与扩展

为了方便，我们常常使用一些扩展表示法：

  • 正则定义（Regular Definition）：为正则表达式命名，以便在其他表达式中引用。 
    1
    2
    3
    letter -> a|b|...|z|A|B|...|Z|_
    digit  -> 0|1|...|9
    id     -> letter(letter|digit)*
  • 扩展运算符：
    • 正闭包（Positive Closure）：r+ 表示 r 出现一次或多次，等价于 rr*。
    • 零次或一次（Optional）：r? 表示 r 出现零次或一次，等价于 r|ε。
    • 字符类（Character Class）：[abc] 等价于 a|b|c。[0-9] 等价于 0|1|...|9。

C 语言无符号数

使用正则定义和扩展，我们可以简洁地描述 Pascal 或 C 语言中的无符号数：

1
2
3
digit  -> [0-9]
digits -> digit+
number -> digits(.digits)?(E[+-]?digits)?

这个正则表达式可以匹配 1946, 11.28, 63.6E8, 1.99E-6 等形式。

词法单元的识别：有穷自动机

描述了模式之后，下一步就是如何识别（Recognize）输入串中与这些模式匹配的词素。这个任务由有穷自动机（Finite Automata, FA）完成。

有穷自动机本质上是一个数学模型，可以看作是状态转换图（Transition Diagram）的形式化表示。

graph TD
    subgraph "理论"
        A[正则表达式（RE）]
    end
    subgraph "实现"
        B[有穷自动机（FA）]
    end
    A -- 描述 --> B
    B -- 识别 --> C[词素]

    style A fill:#cde, stroke:#333
    style B fill:#fde, stroke:#333
    style C fill:#dfd, stroke:#333

状态转换图

状态转换图是一种用于可视化识别过程的有向图：

  • 状态（State）：图中的节点，表示识别过程中的某个情况。
  • 边（Edge）：连接状态的箭头，其标号为输入符号或符号集合。
  • 开始状态（Start State）：图的入口，通常由一个名为 Start 的箭头指向。
  • 接受状态（Accepting State）：用双圈表示的节点。当自动机在读完一个词素后停在接受状态，表示该词素被成功识别。
    • 带有 * 的接受状态表示需要回退（retract）一个字符，因为最后一个字符不属于该词素。

关系运算符的状态转换图

下图展示了用于识别关系运算符（如 <, <=, =, <>, >, >=）的状态转换图。

graph LR
subgraph 关系运算符识别
    direction LR

    %% 初始状态
    start((Start)) -- "Input" --> S0[Initial State];

    %% 主要分支
    S0 -- "<" --> S1["'<' seen"];
    S0 -- "=" --> EQ((EQ));
    S0 -- "\>" --> S6["'>' seen"];

    %% "<" 分支
    S1 -- "=" --> LE((LE));
    S1 -- "\>" --> NE((NE));
    S1 -- "other" --> LT((LT*));

    %% ">" 分支
    S6 -- "=" --> GE((GE));
    S6 -- "other" --> GT((GT*));

    %% 样式定义
    classDef start_node fill:#d3f9d8,stroke:#388e3c,stroke-width:2px,color:#333;
    classDef intermediate_node fill:#e0f2f1,stroke:#00796b,stroke-width:1px,color:#333;
    classDef final_node fill:#ffe0b2,stroke:#f57c00,stroke-width:2px,color:#333;
    classDef other_transition stroke-dasharray: 5 5,stroke:#757575,color:#757575;

    class start start_node;
    class S0,S1,S6 intermediate_node;
    class EQ,LE,NE,LT,GE,GT final_node;
end
  • 当输入为 <= 时，路径为 Start -> Initial -> '<' -> LE。在状态 LE 结束，返回记号 LE。
  • 当输入为 < 后跟一个非 = 或 > 的字符（例如 a）时，路径为 Start -> Initial -> '<' -> LT。状态 LT 是一个带 * 的接受状态，表示已成功识别词素 <，但最后一个字符 a 不属于它，需要回退。返回记号 LT。

有穷自动机的分类

有穷自动机分为两类：

  1. 不确定的有穷自动机（Nondeterministic Finite Automaton, NFA）
    • 对于一个状态和一个输入符号，可能存在多于一个的下一状态。
    • 允许存在 ε\varepsilon-转移，即在不消耗任何输入符号的情况下进行状态转换。
    • NFA 更灵活，更容易从正则表达式构造。
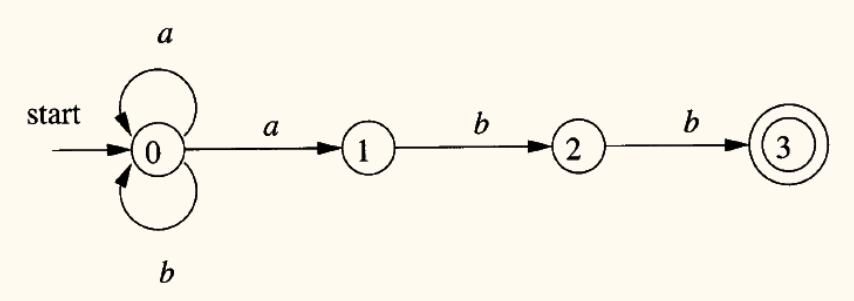
  2. 确定的有穷自动机（Deterministic Finite Automaton, DFA）
    • 对于一个状态和一个输入符号，有且仅有一个确定的下一状态。
    • 没有 ε\varepsilon-转移。
    • DFA 的模拟非常高效，是词法分析器实际执行的基础。

尽管 NFA 和 DFA 的定义不同，但它们的识别能力是等价的。对于任何一个 NFA，都存在一个识别相同语言的 DFA。反之亦然。

因此，词法分析器生成的标准流程是：先将正则表达式转换为 NFA，再将 NFA 转换为等价的 DFA，最后可能对 DFA 进行优化。

从理论到实践：正则表达式与自动机的转换

这是构建词法分析器的核心技术，包含三个主要步骤。

graph LR
    A(正则表达式) -- Thompson 构造法 --> B(NFA);
    B -- 子集构造法 --> C(DFA);
    C -- 状态最小化 --> D(最小化 DFA);

    style A fill:#cde, stroke:#333
    style B fill:#fde, stroke:#333
    style C fill:#edd, stroke:#333
    style D fill:#dfd, stroke:#333

正则表达式到 NFA（Thompson 构造法）

Thompson 构造法是一种递归算法，它为每个正则表达式的组成部分构造一个具有单一开始状态和单一接受状态的 NFA。

  • 基本规则：
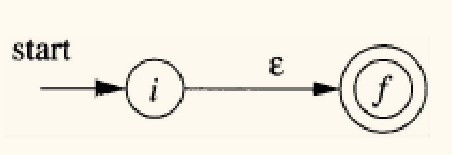
    • 对于 ε\varepsilon：为 ε\varepsilon 构造 NFA
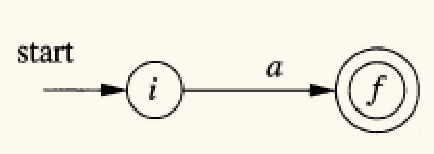
    • 对于符号 a：为字母表中的符号 a 构造 NFA
  • 归纳规则：
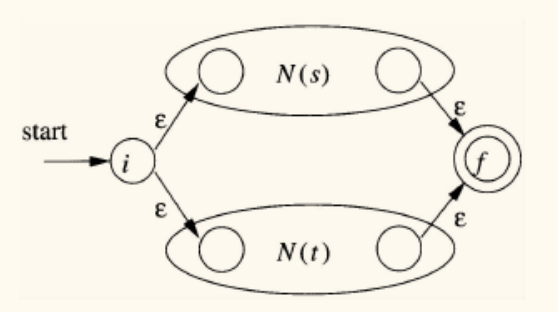
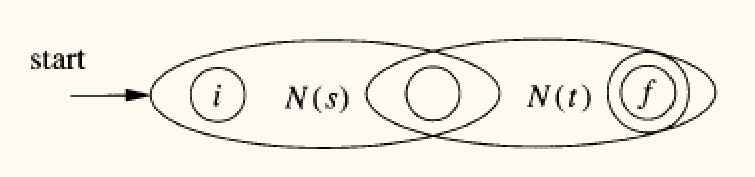
    • 并 r = s | t：引入新的开始和接受状态，通过 ε\varepsilon-转移连接 N(s) 和 N(t)。
    • 连接 r = st：将 N(s) 的接受状态与 N(t) 的开始状态合并。
    • 闭包 r = s*：引入新的开始和接受状态，并添加 ε\varepsilon-转移以实现循环和跳过。

上面的 i, f 都是新状态，表示这个 NFA 的开始和接受状态。

例子

为 (a|b)*abb 构造 NFA。

对于字母表中符号 a 和 b，分别构造 NFA：

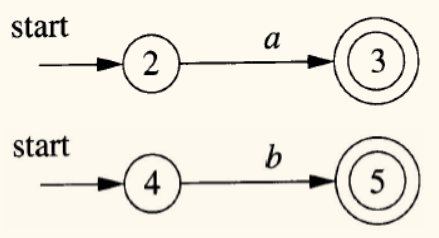
然后，使用并操作将它们组合：

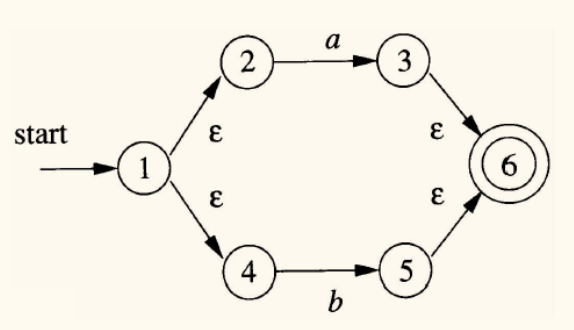
接着，应用闭包操作：

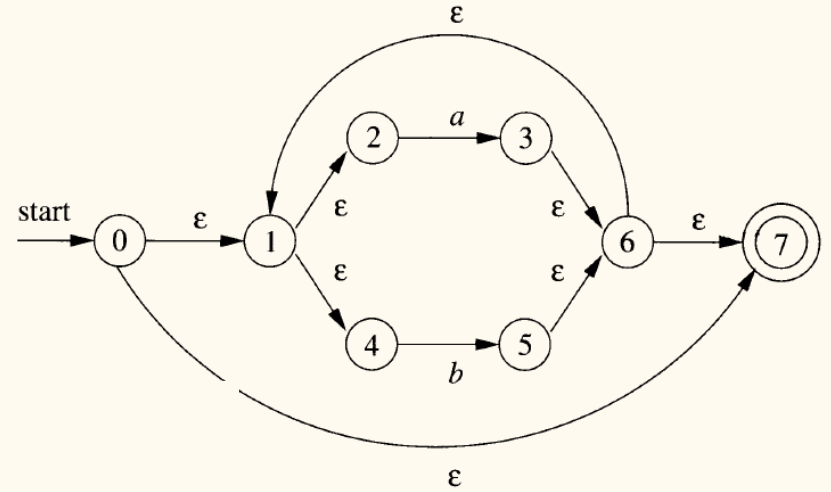
对新的 NFA，再次应用连接操作，依次添加 a, b, b：

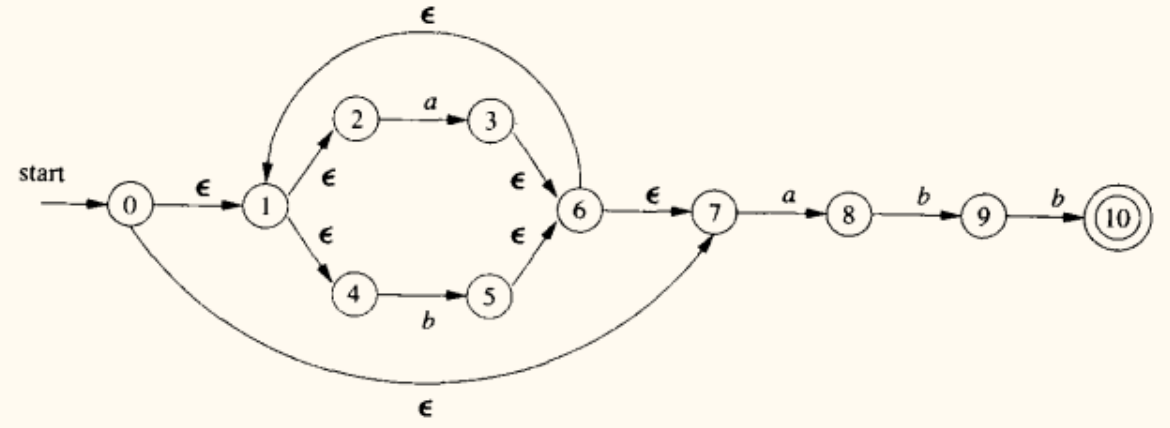
NFA 到 DFA（子集构造法）

子集构造法的核心思想是让 DFA 的每个状态对应 NFA 的一个状态集合。DFA 的一个状态 T 代表了 NFA 在读入某个输入串后可能到达的所有状态的集合。

算法依赖两个关键操作：

  • ε-closure(s)：从 NFA 状态 s 出发，只通过 ε\varepsilon 边能够到达的所有状态的集合（包括 s 本身）。
  • ε-closure(T)：从 NFA 状态集 T 中任意状态出发，只通过 ε\varepsilon-转移能到达的所有状态的集合。
  • move(T, a)：从 NFA 状态集 T 中的任意状态出发，经过一条标号为 a 的边能够到达的状态集合。

算法流程：

  1. DFA 的初始状态是 ε-closure(NFA 的初始状态)。
  2. 从已有的 DFA 状态（它是一个 NFA 状态集 T）开始，对字母表中的每个符号 a：
    • 计算 U = ε-closure(move(T, a))。
    • U 就是一个新的 DFA 状态。
    • 添加一条从 T 到 U 的、标记为 a 的转换边。
  3. 重复步骤 2，直到没有新的 DFA 状态产生。
  4. DFA 的接受状态是所有那些包含了 NFA 至少一个接受状态的 DFA 状态。

ε-closure(T) 伪代码：

子集构造法伪代码：

例子

将 (a|b)*abb 对应的 NFA 转换为 DFA。

  • NFA 的开始状态为 0，接受状态为 10。
  • DFA 的开始状态 A = ε-closure(0) = {0,1,2,4,7}。
  • 计算 Dtran[A, a]：
    • move(A, a) = move({0,1,2,4,7}, a) = {3,8}
    • ε-closure({3,8}) = {1,2,3,4,6,7,8}，这是一个新状态 B。
  • 计算 Dtran[A, b]：
    • move(A, b) = {5}
    • ε-closure({5}) = {1,2,4,5,6,7}，这是一个新状态 C。
  • 计算 Dtran[B, a]：
    • move(B, a) = {3,8}
    • ε-closure({3,8}) = B，状态已存在。
  • 计算 Dtran[B, b]：
    • move(B, b) = {5,9}
    • ε-closure({5,9}) = {1,2,4,5,6,7,9}，这是一个新状态 D。
  • 计算 Dtran[C, a]：
    • move(C, a) = {3,8}
    • ε-closure({3,8}) = B，状态已存在。
  • 计算 Dtran[C, b]：
    • move(C, b) = {5}
    • ε-closure({5}) = C，状态已存在。
  • 计算 Dtran[D, a]：
    • move(D, a) = {3,8}
    • ε-closure({3,8}) = B，状态已存在。
  • 计算 Dtran[D, b]：
    • move(D, b) = {5,10}
    • ε-closure({5,10}) = {1,2,4,5,6,7,10}，这是一个新状态 E。
  • 计算 Dtran[E, a]：
    • move(E, a) = {3,8}
    • ε-closure({3,8}) = B，状态已存在。
  • 计算 Dtran[E, b]：
    • move(E, b) = {5}。
    • ε-closure({5}) = C，状态已存在。

最终得到一个包含 5 个状态的 DFA，其中包含状态 10 的状态集 E 是接受状态：

NFA 状态 DFA 状态 a b
{0, 1, 2, 4, 7} A B C
{1, 2, 3, 4, 6, 7, 8} B B D
{1, 2, 4, 5, 6, 7} C B C
{1, 2, 4, 5, 6, 7, 9} D B E
{1, 2, 4, 5, 6, 7, 10} E B C

DFA 状态最小化

通过子集构造法得到的 DFA 可能包含冗余状态。DFA 最小化算法可以将等价的状态合并，从而得到状态数最少的 DFA。

  • 原理：将 DFA 的状态集划分为多个组。初始时，分为接受状态组和非接受状态组。然后，迭代地细分这些组：如果一个组中的两个状态 s 和 t，在接收到同一个输入符号 a 后，转移到了不同的组中，那么 s 和 t 就是可区分的（distinguishable），需要将它们划分到不同的新组中。
  • 过程：重复细分过程，直到没有组可以再被细分为止。最终每个组内的所有状态都是不可区分的，可以将它们合并为最小化 DFA 的一个状态。

任何正则语言都有一个唯一的（不计同构）状态数目最少的 DFA。

例子

对上例中的 DFA 进行最小化。

初始化分为接受状态组 {E} 和非接受状态组 {A, B, C, D}。

处理非接受状态组 {A, B, C, D}，b 把它们细分为 {A, C}, {B}, {D}。

最后有四个组：{A, C}, {B}, {D}, {E}。

划分完毕，选取 A, B, D, E 作为代表，构造得到最小 DFA。

状态转换表如下：

状态 a b
A B A
B B D
D B E
E B A

词法分析器生成工具

手动编写词法分析器是繁琐且易错的。现代编译器开发广泛使用词法分析器生成工具，如 Lex 或其开源版本 Flex。

词法分析器的状态最小化

在标准的 DFA 最小化算法中，我们通常把所有接受状态作为初始的一个集合，所有非接受状态作为另一个集合。但是，在词法分析器中，这样做是错误的。例如，一个接受状态可能表示识别了「关键字 if」，而另一个接受状态可能表示识别了「标识符」。如果我们把这两个状态合并，词法分析器就无法区分它们了。

正确的做法是，将初始集合划分得更细致一些。具体划分规则如下：

  • 所有非接受状态构成一个集合。
  • 每一个模式（pattern） 的接受状态分别构成一个独立的集合。
    • 也就是说，如果 DFA 能识别三种 Token，那么对应这三种 Token 的接受状态就应该被分成三个独立的集合。
例子

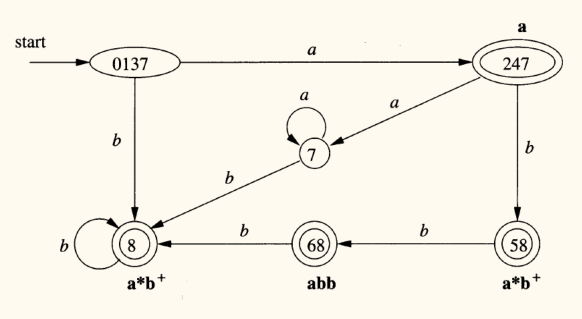
初始划分增加死状态 Φ\Phi，用作词法分析的 DFA 可以丢掉 Φ\Phi

死状态（Dead State） 是一个陷阱状态，一旦进入就无法再到达任何接受状态。在进行状态划分时，它自己会形成一个独立的集合。

不过在实际的词法分析器实现中，通常会省略这个状态，因为如果没有为某个状态定义某个字符的转移，就默认进入了错误处理程序，效果类似。

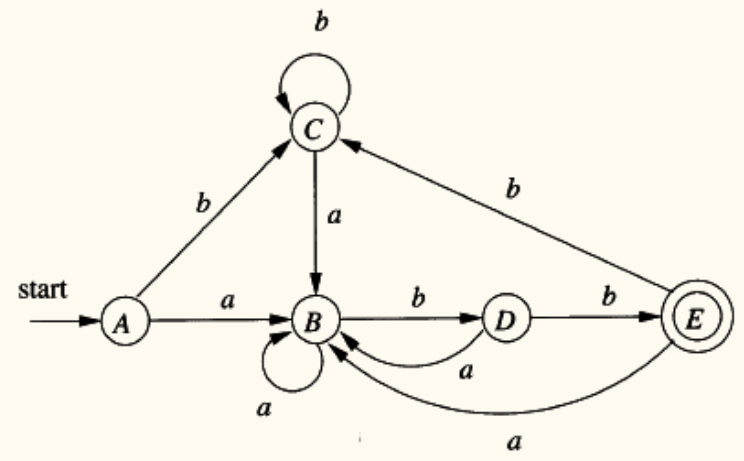
初始划分为 {0137, 7}, {247}, {8, 58}, {68}, {Φ}：

  • {0137, 7}：这是非接受状态集合。从图中看，状态 0137 和 7 是中间状态，不是双圈表示的接受状态。
  • {247}：这是一个接受状态集合。它对应于图中标签为 a 的模式。
  • {8, 58}：这是另一个接受状态集合。虽然有两个状态，但它们都对应于同一个模式 a*b+。
  • {68}：这是第三个接受状态集合，对应模式 abb。
  • {Φ}：这是死状态集合（图中未画出）。

Lex/Flex 工作原理

开发者提供一个包含正则表达式和相应动作（C 代码）的规约文件（.l 文件）。Lex/Flex 工具读取这个文件，并自动生成一个名为 yylex() 的 C 函数，这个函数就是一个高效的词法分析器。

graph LR
    A[Lex 规约文件（lex.l）] --> B{Lex 编译器};
    B --> C[C 源文件（lex.yy.c）];
    C --> D{C 编译器};
    D --> E[可执行词法分析器（a.out）];

    style A fill:#cde, stroke:#333
    style B fill:#fde, stroke:#333
    style C fill:#edd, stroke:#333
    style D fill:#ffd, stroke:#333
    style E fill:#dfd, stroke:#333

Lex 程序结构

一个 Lex 程序通常由三部分组成，以 %% 分隔：

1
2
3
4
5
{声明部分}
%%
{转换规则}
%%
{辅助函数}
  • 声明部分：定义正则表达式的别名（正则定义）和 C 语言的变量、常量等。
  • 转换规则：核心部分，每一条规则由一个模式（正则表达式）和一个动作（{} 中的 C 代码）组成。当词法分析器匹配到某个模式时，就执行对应的动作。
  • 辅助函数：动作代码中可能调用的一些自定义 C 函数。

Lex 规则示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
%{
    // C 代码声明部分
%}

%%
/* 规则部分 */
"if"      { return IF; }
"else"    { return ELSE; }
[a-z]+    { yylval = install_id(); return ID; } /* 标识符 */
[0-9]+    { yylval = install_num(); return NUMBER; } /* 数字 */
\n        ; /* 忽略换行符 */
[ \t]+    ; /* 忽略空白符 */
.         { /* 处理其他所有字符 */ }
%%

/* 用户辅助函数部分 */
int install_id() { ... }
int install_num() { ... }

冲突解决

当输入串可能匹配多个模式时，Lex 使用以下两条规则解决冲突：

  1. 最长匹配原则（Longest Match）：总是选择能匹配输入流中最长前缀的模式。
    • 例如在 ifx 的例子中，if 作为一个关键字是可能的匹配，但 ifx 作为一个标识符是更长的匹配。最长匹配原则确保了 ifx 被整体识别为一个标识符，而不是 if 关键字后面跟着一个 x 标识符。
  2. 最先匹配原则（First Rule Wins）：如果多个模式匹配了相同长度的最长前缀，则选择在 Lex 规约文件中最先出现的那条规则。
    • 这就是为什么通常将关键字（如 if, else, while）的规则放在通用标识符 id 规则之前的原因。