语法制导的翻译

发表于 2025-10-14 更新于 2025-10-21 Waline：阅读次数：本文字数： 4.8k 阅读时长 ≈ 17 分钟

语法制导翻译导论

在编译流程中，语法分析器（Parser）成功地验证了程序的结构并构建了语法分析树。然而，这棵树仅仅描述了程序的「骨架」，并未涉及其「血肉」——即程序的语义（semantics）。语法制导翻译（Syntax-Directed Translation）正是连接语法结构和语义处理的桥梁。

语法制导翻译

语法制导翻译是一种编译器模型，它通过为文法中的产生式关联属性（attributes）和语义规则（semantic rules），将翻译（如类型检查、代码生成等）任务与语法分析过程紧密结合起来。

其核心思想是，程序语言中一个构造的含义（语义），可以由其子构造的含义组合而成。

自下而上：表达式 x + y 的类型，由 x 的类型、y 的类型以及运算符 + 的语义共同决定。
自上而下：在声明 int x; 中，变量 x 的类型是由其左侧的类型说明符 int 决定的。

为了形式化地描述这一过程，我们引入两个核心工具：语法制导定义（SDD）和语法制导翻译方案（SDT）。

语法制导定义

语法制导定义（Syntax-Directed Definition, SDD）是一种高度抽象、与具体实现无关的规范。它将文法与语义规则清晰地分离开来。

SDD 告诉我们什么（what）被计算，但并不指定计算的时机（when）。

语法制导定义

一个 SDD 由以下两部分组成：

属性（Attributes）：与每个文法符号（终结符或非终结符）相关联的值。例如，一个表示表达式的非终结符 $E$ 可能有一个 $val$ 属性表示表达式的值，以及一个 $type$ 属性表示其类型。
语义规则（Semantic Rules）：与每个产生式相关联，用于描述如何计算该产生式中符号的属性值。

对于分析树中的一个节点 $N$ （其标号为文法符号 $X$ ），它的属性 $a$ 记为 $N.a$ 或 $X.a$ 。语义规则定义了这些属性值之间的依赖关系。

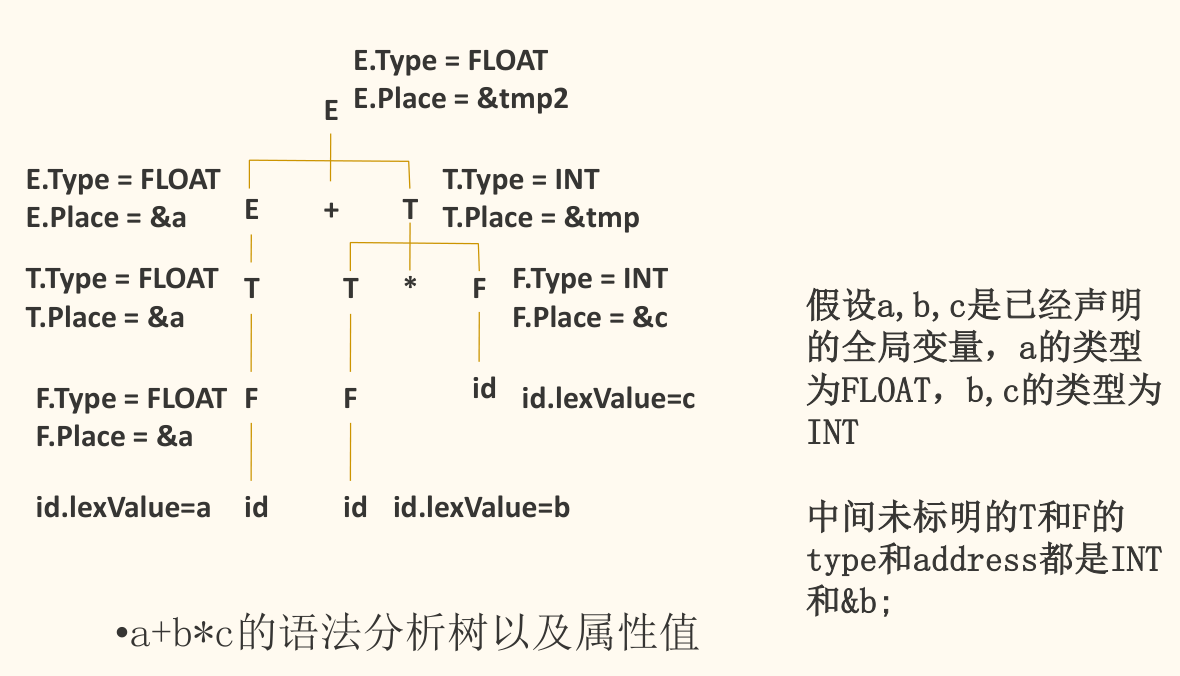
综合属性与继承属性

属性根据其值的计算方式，可以分为两大类，这决定了信息在语法分析树中的流动方向。

综合属性（Synthesized Attribute）
- 定义：在分析树的某个节点 $N$ 上，一个综合属性的值是由 $N$ 的子节点或 $N$ 自身的属性值计算出来的。
- 信息流：自下而上（Bottom-Up）。
- 用途：常用于「汇总」子结构的信息，例如计算表达式的值、确定表达式的类型、生成子结构的中间代码等。
继承属性（Inherited Attribute）
- 定义：在分析树的某个节点 $N$ 上，一个继承属性的值是由 $N$ 的父节点、兄弟节点或 $N$ 自身的属性值计算出来的。
- 信息流：自上而下（Top-Down）或自左向右（Sideways）。
- 用途：常用于传递上下文信息，例如将声明中的类型信息传递给标识符列表，或者控制代码生成的跳转目标地址。

考虑 C 语言中的声明 int i, j, k;。其文法可能类似 $D \to T L$ （声明 $\to$ 类型列表）， $L \to L,\, \mathbf{id} \mid \mathbf{id}$ 。在分析树中，标识符 i, j, k 的类型信息（int）是从它们的共同祖先节点 $T$ 处继承下来的。语义规则可能是 $L.type = T.type$ ，将类型信息从父节点 $T$ 传递给子节点 $L$ 。

终结符的属性

终结符可以拥有综合属性，这些属性值通常由词法分析器提供（例如， $\mathbf{id}$ 的 $lexval$ ， $\mathbf{num}$ 的 $val$ ）。

终结符没有继承属性，因为它们是树的叶子节点，没有子结构来继承信息。

桌面计算器的 SDD

这个 SDD 用于计算一个包含加法、乘法和括号的算术表达式的值。

产生式	语义规则	属性类型
$L \to E \mathbf{n}$	$L.val = E.val$	综合属性
$E \to E_1 + T$	$E.val = E_1.val + T.val$	综合属性
$E \to T$	$E.val = T.val$	综合属性
$T \to T_1 * F$	$T.val = T_1.val \times F.val$	综合属性
$T \to F$	$T.val = F.val$	综合属性
$F \to (E)$	$F.val = E.val$	综合属性
$F \to \mathbf{digit}$	$F.val = \mathbf{digit}.lexval$	综合属性

在这个例子中，所有非终结符（ $L, E, T, F$ ）都只有一个综合属性 $val$ 。每个产生式头的 $val$ 属性都是由其产生式体中符号的 $val$ 属性计算得出的。

属性值的计算

注释分析树与依赖图

为了可视化属性的计算过程，我们可以使用注释分析树（Annotated Parse Tree）。它是在语法分析树的基础上，为每个节点标注出其属性值的分析树。

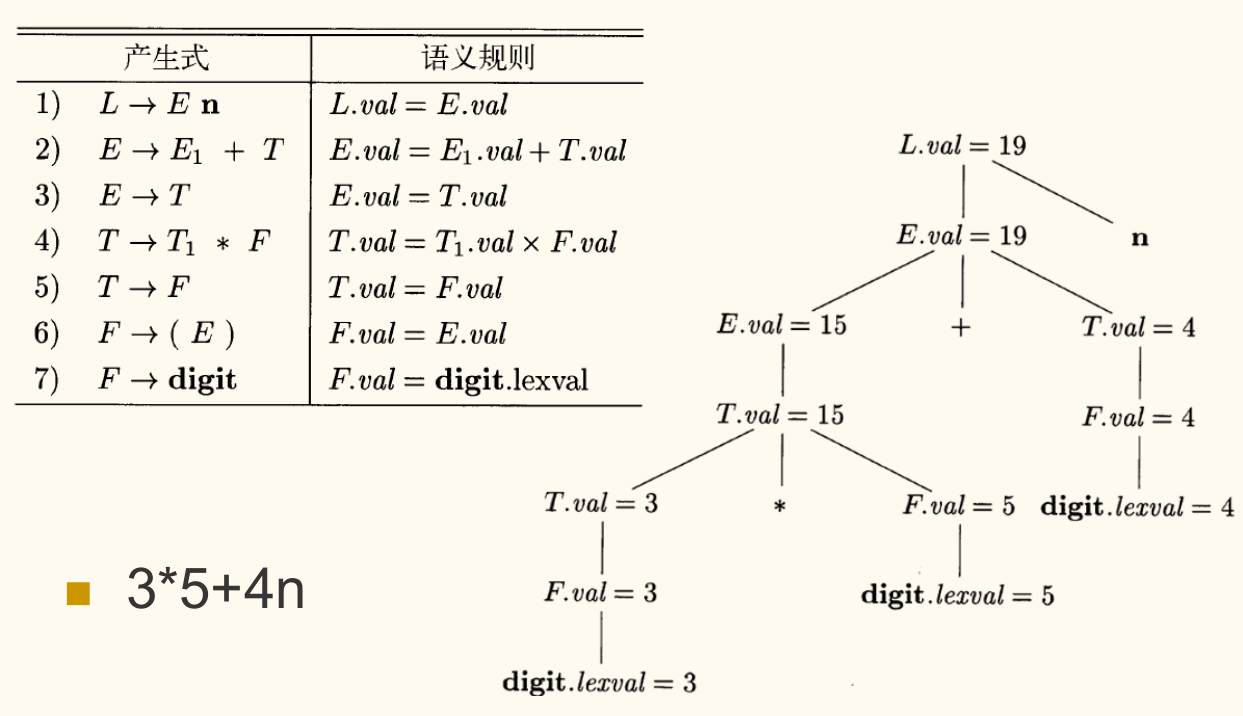
然而，在计算属性值之前，我们必须确定一个正确的计算顺序。例如，要计算 $E.val = E_1.val + T.val$ ，必须先得到 $E_1.val$ 和 $T.val$ 的值。这种依赖关系可以通过依赖图来描述。

依赖图

对于一棵特定的分析树，其依赖图（Dependency Graph）是一个有向图，用于描述该树中各个属性实例之间的信息流。

节点：树中每个节点的每个属性都对应依赖图中的一个节点。
边：如果属性 $b$ 的值依赖于属性 $c$ 的值，那么依赖图中就有一条从 $c$ 对应的节点到 $b$ 对应的节点的有向边。

求值顺序

属性的计算必须遵循依赖图的拓扑排序（Topological Sort）。

任何一个合法的求值顺序都是依赖图的一个拓扑排序。
如果依赖图中存在环（cycle），则说明属性之间存在循环定义（如 $A.s = B.i;\; B.i = A.s + 1;\;$ ），这样的 SDD 是没有意义的，其属性值无法计算。

虽然对任意 SDD 检查是否存在循环依赖是困难的，但我们可以定义一些良定义的 SDD 子类，它们保证了依赖图无环，并且具有高效的求值策略。

两类重要的 SDD

S-属性的 SDD

一个 SDD 如果只包含综合属性，则称之为 S-属性的 SDD（S-Attributed SDD）。

S-属性的 SDD 非常重要，因为它们具有清晰的、自下而上的计算模型。

求值顺序：可以在对分析树进行「后序遍历」的过程中完成所有属性的计算。因为信息流完全是自底向上的，在访问一个节点之前，它的所有子节点都已被访问，这意味着计算其综合属性所需的所有值都已准备就绪。
与语法分析的结合：S-属性的求值过程与自底向上（LR）语法分析完美契合。在 LR 分析器进行归约操作时，产生式体中所有符号的属性值都已计算完毕并存在于分析栈中，此时正是计算产生式头综合属性的最佳时机。

语义规则不应有复杂的副作用，要求不影响其他属性的求值。没有副作用的 SDD 称为「属性文法」。

属性文法没有副作用，但增加了描述的复杂度。比如语法分析时如果没有副作用，标识符表就必须作为属性传递。可以把标识符表作为全局变量，然后通过副作用函数来添加新标识符。

受控的副作用：

不会对属性求值产生约束，即可以按照任何拓扑顺序求值，不会影响最终结果
或者对求值过程添加简单的约束

L-属性的 SDD

S-属性的 SDD 功能有限，因为它无法处理需要上下文信息（即继承属性）的场景。L-属性的 SDD 放宽了这一限制，允许使用继承属性，但对其施加了特定约束以保证高效求值。

L-属性的 SDD

一个 SDD 是 L-属性的 SDD（L-Attributed SDD），如果对于它的每个产生式 $A \to X_1 X_2 \dots X_n$ ，其关联的每条语义规则计算的属性都满足：

要么是一个综合属性。
要么是 $X_i$ $X_{i}$ 的一个继承属性，并且其计算只依赖于：
- $A$ 的继承属性。
- $X_i$ 左侧兄弟 $X_j$ （ $j < i$ ）的继承或综合属性。
- $X_i$ 自身的其他属性（但不能形成循环依赖）。

核心思想：L-属性的 L 代表 Left-to-right，在从左到右处理产生式体 $X_1 X_2 \dots X_n$ 的过程中，计算 $X_i$ 的继承属性所需的所有信息都已经可用。

信息流：依赖图的边总是从左到右，或从上到下，不会「向左回溯」。
与语法分析的结合：L-属性的求值过程与自顶向下（LL）语法分析非常契合。在递归下降分析中，我们可以：
- 通过「函数参数」传递继承属性。
- 通过「函数返回值」传递综合属性。

所有 S-属性的 SDD 都是 L-属性的 SDD，因为它们满足 L-属性定义的第一个条件——都是综合属性。

语法制导翻译方案

SDD 是一种抽象规范，而语法制导翻译方案（Syntax-Directed Translation Scheme, SDT）是一种具体的实现方法。

语法制导翻译方案

一个 SDT 是在产生式体中嵌入了语义动作（semantic actions）的上下文无关文法。

语义动作是用 {} 括起来的程序代码片段。

SDT 将语义规则的计算时机与语法分析过程中的特定时刻绑定在一起。

执行时机：一个语义动作在语法分析过程中被执行的时机，取决于它在产生式中的位置。当分析器识别到该动作之前的所有符号时，该动作就会被执行。
基本实现：可以先构造完整的语法分析树，然后将语义动作作为额外的子节点插入。对这棵新树进行深度优先遍历，在访问到动作节点时执行它。

后缀翻译方案

后缀 SDT

如果一个 SDT 的所有语义动作都位于产生式的最右端，则称之为后缀翻译方案（Postfix SDT）。

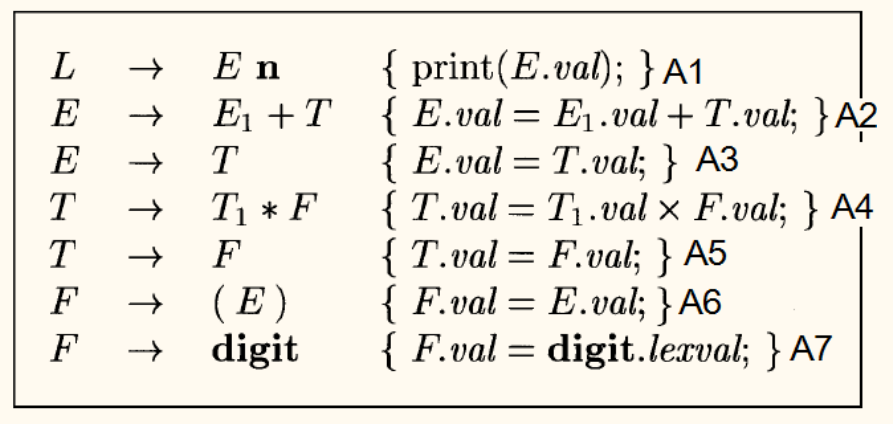
后缀 SDT 非常重要，因为它们可以直接在 LR 语法分析过程中实现。

实现：当 LR 分析器执行归约操作时，立即执行与该产生式关联的（位于末尾的）语义动作。
与 S-属性 SDD 的关系：任何 S-属性的 SDD 都可以转换为一个后缀 SDT。只需将计算综合属性的语义规则作为动作，放置在对应产生式的末尾即可。

使用分析栈实现后缀 SDT

在 LR 分析器中，分析栈不仅可以保存状态，还可以并行地保存与文法符号关联的属性值。
当要按产生式 $A \to XYZ$ 归约时：

$Z$ 的属性值位于栈顶。
$Y$ 的属性值位于次栈顶。
$X$ 的属性值位于第三个位置。
此时，可以执行动作 { A.val = f(X.val, Y.val, Z.val); }，然后用归约后的 $A$ 及其属性值替换栈顶的 $X, Y, Z$ 。

桌面计算器的后缀 SDT 如下：

产生式	语义动作（在分析栈上实现）
$L \to E \mathbf{n}$	`{ print(stack[top-1].val); top -= 1; }`
$E \to E_1 + T$	`{ stack[top-2].val += stack[top].val; top -= 2; }`
$T \to T_1 * F$	`{ stack[top-2].val *= stack[top].val; top -= 2; }`
…	…

这里的 stack[top] 对应产生式最右边的符号，stack[top-2] 对应左边的符号。归约后，这些符号出栈，新的非终结符入栈，其属性值被计算并存放在新的栈顶记录中。

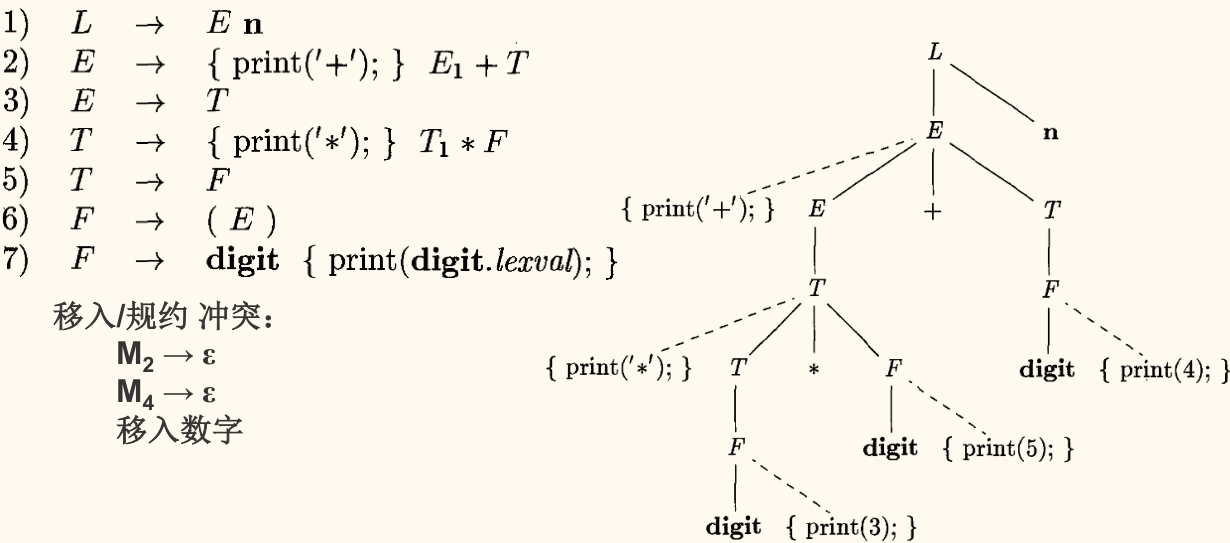
在产生式中嵌入动作

对于 L-属性的 SDD，其对应的 SDT 通常需要在产生式体中间嵌入动作。

动作的执行时机：一个嵌入的动作在它左边的所有符号都被处理完毕后立即执行。
在自顶向下分析中：在递归下降分析器中，这相当于在调用不同子过程之间插入代码片段，当分析器准备展开动作之后的非终结符时，该动作被执行。
在自底向上分析中：分析中，当动作之前的所有符号都被处理并移入栈顶时，该动作被执行。这会使实现变得复杂，一种常见的技巧是，将动作 {a} 替换为一个专门的标记非终结符 $M$ ，并增加产生式 $M \to \varepsilon$ 。当分析器归约 $M \to \varepsilon$ 时，就执行动作 a。

消除左递归时的 SDT 转换

当我们将一个左递归的文法转换为适合自顶向下分析的非左递归文法时，其对应的 SDT 也需要进行转换。这通常需要巧妙地使用继承属性来传递左递归中「累积」的值。

如果动作不涉及属性值，可以把动作当作终结符号进行处理，然后消除左递归。

一般转换形式：

$\begin{aligned} A &\to A_1 Y\left\lbrace A.a = g(A_1.a, Y.y) \right\rbrace\\ A &\to X \left\lbrace A.a = f(X.x) \right\rbrace \end{aligned}$

可以转换为：

$\begin{aligned} A &\to X \left\lbrace R.i = f(X.x) \right\rbrace R \left\lbrace A.a = R.s \right\rbrace\\ R &\to Y \left\lbrace R_1.i = g(R.i, Y.y) \right\rbrace R_1 \left\lbrace R.s = R_1.s \right\rbrace\\ R &\to \varepsilon \left\lbrace R.s = R.i \right\rbrace \end{aligned}$

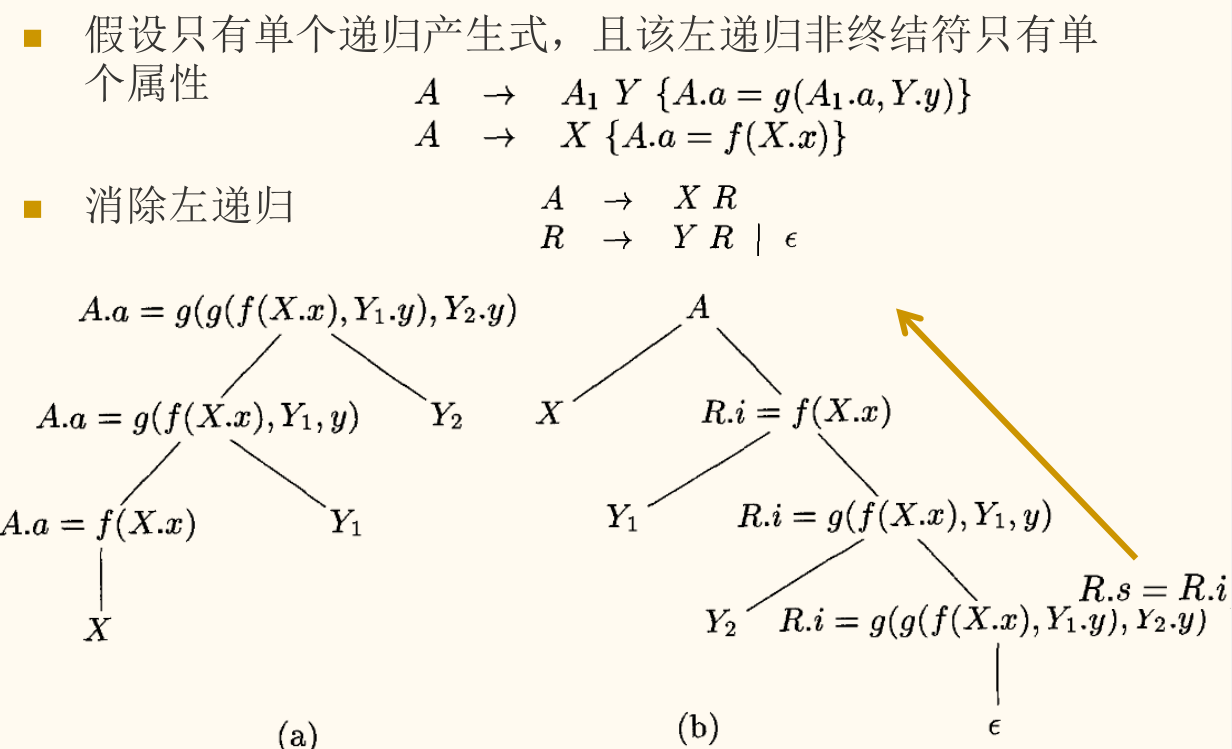
表达式求值的 SDT 转换

原始左递归 SDD（S-属性）

$\begin{aligned} E &\to E_1 + T \quad &&\{ E.val = E_1.val + T.val \} \\ E &\to T \quad &&\{ E.val = T.val \} \end{aligned}$

消除左递归后的 SDD（L-属性）

$\begin{aligned} E &\to T E' \quad &&\{ E'.inh = T.val;\; E.val = E'.syn; \} \\ E' &\to + T E'_1 \quad &&\{ E'_1.inh = E'.inh + T.val;\; E'.syn = E'_1.syn; \} \\ E' &\to \varepsilon \quad \ &&\{ E'.syn = E'.inh; \} \end{aligned}$

综合属性 $T.val$ 作为继承属性 $E'.inh$ 被传递给 $E'$ 。
$E'$ 通过递归调用，不断用新的 $T.val$ 更新这个继承属性，并将最终结果通过综合属性 $E'.syn$ 向上返回。

L-属性定义的实现

L-属性的 SDD 与递归下降分析法是天作之合。我们可以将 SDD 直接翻译成一个递归下降的翻译器。

每个非终结符 A 对应一个函数 A()。
A 的继承属性作为函数 A() 的参数。
A 的综合属性作为函数 A() 的返回值（或者通过指针/引用参数返回）。
函数体内部，根据当前的输入符号选择一个产生式，并按从左到右的顺序处理产生式中的每个符号：
- 遇到终结符，就匹配输入。
- 遇到非终结符 X，就调用函数 X()，并传入其所需的继承属性值，接收其返回的综合属性值。
- 遇到语义动作，就直接执行相应的代码。

while 语句的翻译

考虑一个 while 语句的 SDD，它有继承属性 next（语句结束后跳转的标号）和综合属性 code（生成的代码）。

L1:                 // 循环开始的标签（也是 S1 结束后跳回的地方）
    <C.code>        // C 的代码
    if (C.value == false) goto S.next  // 如果 C 为假，跳出循环
L2:                 // 循环体的标签（C 为真时跳到这里）
    <S1.code>       // S1 的代码
    goto L1         // S1 执行完后，无条件跳回 L1 检查条件
S.next:             // 循环结束后的下一条语句

// SDD 规则
S -> while (C) S1
    {
        // 1. 生成新标签
        L1 = new(); L2 = new();
        // 2. 设置 C 的继承属性
        C.true = L2; C.false = S.next;
        // 3. 设置 S1 的继承属性
        S1.next = L1;
        // 4. 计算 S 的综合属性
        S.code = label(L1) || C.code || label(L2) || S1.code;
    }

对应的递归下降函数 S() 可能如下：

string S(label next) { // 'next' 是继承属性
    if (lookahead == WHILE) {
        match(WHILE); match('(');
        label L1 = new_label();
        label L2 = new_label();
        string c_code = C(L2, next); // 传入继承属性 true 和 false
        match(')');
        string s1_code = S(L1); // 传入继承属性 next
        // 返回综合属性 code
        return "label " + L1 + "\n" + c_code + "label " + L2 + "\n" + s1_code;
    } else {
        // …处理其他语句类型…
    }
}

边扫描边生成属性

在前面的 while 语句翻译的例子中，我们使用 ||（并置）操作符将各个代码片段（label(L1)、C.code、S1.code 等）组合成一个单一的、巨大的综合属性 S.code。

存在的问题

当属性值的体积非常大时，例如 code 属性可能是一个包含上百 K 代码的字符串，对这样的属性值进行并置等运算的效率会非常低下。

一种更高效的策略是「边扫描边生成」，即不再构造一个巨大的字符串，而是在语法分析的过程中，在适当的时机将各个代码片段直接「打印」或「发出」。

基本思想与条件

基本思想：将一个大的综合属性（主属性）的计算，分解为在语法分析过程中逐步生成它的各个部分，并将这些部分增量式地添加到最终的属性值中。

条件：

存在一个「主属性」（如 code），且该主属性是综合属性。
在产生式中，主属性是通过连接（并置）产生式体中非终结符号的主属性，以及一些其他元素（如 label L1）得到的。
各非终结符号的主属性的连接顺序，与其在产生式体中的顺序相同。

while 语句翻译（增量式）

假设我们不再返回 code 字符串，而是约定每个非终结符的翻译函数（如 C() 和 S()）会直接打印它们的代码。

原始 SDT（返回 S.code）：

1
2
3

S -> while ( { L1=new(); L2=new(); C.false=S.next; C.true=L2; }
     C )     { S1.next=L1; }
     S1      { S.code=label || L1 || C.code || label || L2 || S1.code; }

增量式 SDT（直接 print）：

1
2
3

S -> while ( { L1=new(); L2=new(); C.false=S.next; C.true=L2; print("label", L1); }
     C )     { S1.next=L1; print("label", L2); }
     S1      { }

在这个新的 SDT 中：

在分析 C 之前，我们立即 print("label", L1)。
然后分析 C（调用 C()），C 函数内部会负责 print(C.code)。
在分析 S1 之前，我们立即 print("label", L2)。
最后分析 S1（调用 S()），S() 函数内部会负责 print(S1.code)。

这种方法的前提是所有相关的非终结符（如 C 和 S1）都遵循相同的约定，即在执行时打印自己的代码。

递归下降实现：

这种增量式 SDT 可以非常自然地在递归下降分析器中实现：

void S(label next) { // 'next' 是继承属性
    label L1, L2;
    if (lookahead == WHILE) {
        match(WHILE);
        match('(');
        L1 = new_label();
        L2 = new_label();

        // 增量式「发出」代码
        print("label", L1);

        C(next, L2); // 传入继承属性，C() 内部会打印 C.code

        match(')');

        // 增量式「发出」代码
        print("label", L2);

        S(L1); // 传入继承属性，S() 内部会打印 S1.code
    }
    else { ... }
}

应用实例

构造抽象语法树（AST）

语法制导翻译是构建 AST 的核心技术。我们可以定义一个综合属性 $nptr$ （node pointer），它的值是指向为该语法结构创建的 AST 节点的指针。

为简单表达式构造 AST 的 SDD

产生式	语义规则
$E \to E_1 + T$	$E.nptr = \mathbf{new}\ \text{Node}(\text{\textquotedblleft$+$\textquotedblright},\, E_1.nptr,\, T.nptr)$
$E \to E_1 - T$	$E.nptr = \mathbf{new}\ \text{Node}(\text{\textquotedblleft$-$\textquotedblright},\, E_1.nptr,\, T.nptr)$
$E \to T$	$E.nptr = T.nptr$
$T \to (E)$	$T.nptr = E.nptr$
$T \to \mathbf{id}$	$T.nptr = \mathbf{new}\ \text{Leaf}(\mathbf{id},\, \mathbf{id}.entry)$
$T \to \mathbf{num}$	$T.nptr = \mathbf{new}\ \text{Leaf}(\mathbf{num},\, \mathbf{num}.val)$

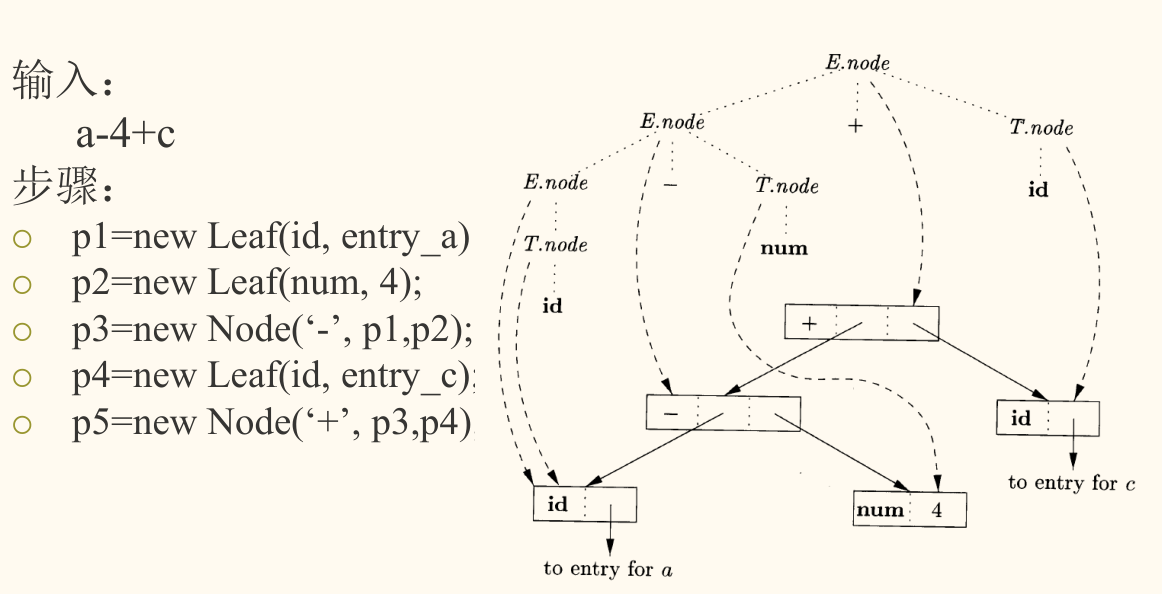
处理类型声明

处理类似 int a[2][3] 这样的类型声明是展示继承属性强大功能的经典例子。我们需要将基本类型 int 传递给数组维度 [2][3] 来构造最终的类型。

类型声明的 L-属性 SDD

文法：

$\begin{aligned} T &\to B C \\ B &\to \mathbf{int} \mid \mathbf{float} \\ C &\to [\mathbf{num}] C_1 \mid \varepsilon \end{aligned}$

SDD：

产生式	语义规则
$T \to B C$	$T.type = C.type;\; C.base = B.type;$
$B \to \mathbf{int}$	$B.type = \text{integer};$
$B \to \mathbf{float}$	$B.type = \text{float};$
$C \to [\mathbf{num}] C_1$	$C.type = \text{array}(\mathbf{num}.val, C_1.type);\; C_1.base = C.base;$
$C \to \varepsilon$	$C.type = C.base;$

$B$ 的综合属性 $type$ （基本类型）通过 $T \to BC$ 产生式，被赋给 $C$ 的继承属性 $base$ 。
继承属性 $base$ 沿着 $C$ 的产生式链（ $C \to [\mathbf{num}] C_1$ ）向下传递。
当 $C$ 的推导最终到达 $\varepsilon$ 时，继承的 $base$ 类型作为基础，通过综合属性 $type$ 开始自下而上地构建完整的数组类型。

flowchart TB
    subgraph T_production [T → B C]
        direction LR
        B_node[B] -->|B.type| C_node[C]
        C_node -->|C.type| T_node[T]
    end

    subgraph B_productions [B 产生式]
        direction TB
        B_int[B → int] -->|B.type = integer| B_type1
        B_float[B → float] -->|B.type = float| B_type2
    end

    subgraph C_productions [C 产生式]
        direction TB
        C_array[C → <b>num</b> C1] -->|C.type = array<br>C1.base = C.base| C1_node[C1]
        C_eps[C → ε] -->|C.type = C.base| C_eps_out
    end

    %% 属性流连接
    B_type1 -->|base| C_base_in
    B_type2 -->|base| C_base_in
    C_base_in[C.base] -.->|继承属性传递| C_array
    C_base_in -.->|继承属性传递| C_eps

    %% 样式定义
    classDef production fill:#e1f5fe,stroke:#01579b,stroke-width:2px
    classDef attribute fill:#f3e5f5,stroke:#4a148c,stroke-width:2px
    classDef terminal fill:#e8f5e8,stroke:#1b5e20,stroke-width:2px
    classDef thisnode fill:#fff3e0,stroke:#ef6c00,stroke-width:2px
    classDef output fill:#ffebee,stroke:#b71c1c,stroke-width:2px

    class T_production,B_productions,C_productions production
    class B_type1,B_type2,C_base_in attribute
    class B_int,B_float,C_array,C_eps terminal
    class B_node,C_node,C1_node,T_node thisnode
    class C_eps_out output