代码生成

发表于 2025-11-25 更新于 2025-12-02 Waline：阅读次数：本文字数： 8.3k 阅读时长 ≈ 30 分钟

代码生成概述

代码生成是编译过程的最后一个阶段。在经历了词法分析、语法分析、语义分析和中间代码生成（及优化）之后，编译器终于要将与机器无关的中间表示（Intermediate Representation, IR）转换成依赖于特定目标机器的目标代码（通常是汇编语言或机器码）。

graph LR
    A[📄 源程序] --> B{🔄 前端};
    B --> C[⚙️ 中间代码];
    C --> D[(🚀 代码优化器)];
    D --> E[⚙️ 优化后中间代码];
    E --> F{🎯 后端：代码生成器};
    F --> G[💻 目标程序];
    
    %% 样式定义
    classDef default fill:#f8f9fa,stroke:#495057,stroke-width:2px,color:#212529;
    classDef process fill:#e3f2fd,stroke:#1565c0,stroke-width:2px;
    classDef decision fill:#fff3e0,stroke:#ef6c00,stroke-width:2px;
    classDef output fill:#e8f5e8,stroke:#2e7d32,stroke-width:2px;
    
    %% 应用样式
    class A,G output;
    class B,F decision;
    class C,D,E process;
    
    %% 连接线样式
    linkStyle default stroke:#666,stroke-width:2px,fill:none;

代码生成器是编译器的后端，它不仅要保证生成的代码在语义上与源程序等价（正确性），还要力求高效（在空间和时间上）。这个过程通常包含三个相互关联的核心任务：

指令选择（Instruction Selection）：为 IR 中的每个或每组操作选择最合适的目标机指令。这并非简单的「一对一」翻译，因为目标机可能提供多种指令来实现同一功能，而它们的代价（如执行速度、指令长度）各不相同。
寄存器分配与指派（Register Allocation and Assignment）：合理地将程序中的变量和临时值分配到有限的寄存器中。由于寄存器访问速度远快于内存，优秀的寄存器分配策略对程序性能至关重要。
指令排序（Instruction Ordering）：安排指令的执行顺序以优化性能，例如利用指令流水线、避免数据冒险等。

最优代码生成的挑战

为任意一个源程序生成「最优」的目标代码是一个非常困难的问题，在理论上是不可判定的。因此，编译器设计者通常采用启发式算法，在编译时间和代码质量之间做出权衡，以生成「足够好」的代码。

目标机器模型

为了具体讨论代码生成，我们首先需要一个假想的目标机器模型。本章将采用一个简化的、类似 RISC (精简指令集计算机) 的三地址指令机。

指令集

指令类型	格式	含义
加载	`LD dst, addr`	`dst = addr`，将内存地址 `addr` 的内容加载到寄存器 `dst`。
存储	`ST x, r`	`x = r`，将寄存器 `r` 的内容存储到内存地址 `x`。
计算	`OP dst, src1, src2`	`dst = src1 OP src2`，对 `src1` 和 `src2` 进行运算，结果存入 `dst`。
无条件跳转	`BR L`	无条件跳转到标号为 `L` 的指令。
条件跳转	`Bcond r, L`	如果寄存器 `r` 满足特定条件（如大于零、等于零），则跳转到 `L`。

寻址模式

寻址模式决定了指令如何定位其操作数。

模式	语法	描述	代价
变量名	`x`	直接使用变量 `x` 的地址。	1
寄存器	`r`	直接使用寄存器 `r`。	0
变址	`a(r)`	地址为 `a` 的基地址加上寄存器 `r` 中的值。常用于数组访问。	1
间接寻址	`*r`	寄存器 `r` 的内容是一个地址，操作数在该地址中。	1
间接变址	`*constant(r)`	先计算 `r` 的内容 + `constant` 得到地址 `A`，再取地址 `A` 处存放的值。常用于指针和结构体字段访问。	1
立即数	`#constant`	操作数就是常数 `constant` 本身。	1

指令代价模型

为了评估生成代码的质量，我们定义一个简单的代价模型：

一条指令的代价 = 1 + 其各操作数寻址模式的代价之和。

指令代价计算

LD R0, R1：代价为 1 + 0 = 1（源操作数是寄存器，代价为 0）。
LD R0, M：代价为 1 + 1 = 2（源操作数是内存地址，代价为 1）。
LD R1, *100(R2)：代价为 1 + 1 = 2（源操作数是间接变址，代价为 1）。

指令选择

指令选择是将 IR 语句翻译成目标指令序列的过程。即使是简单的 IR 语句，也可能对应多种指令序列。

简单算术运算

考虑三地址码 x = y + z。一个直接但可能低效的翻译是：

LD R0, y       // R0 = y
LD R1, z       // R1 = z
ADD R0, R0, R1 // R0 = R0 + R1
ST x, R0       // x = R0

然而，如果我们的目标机支持 ADD R0, R0, z 这样的指令（一个操作数在寄存器，一个在内存），代码就可以更高效：

1
2
3

LD R0, y      // R0 = y
ADD R0, R0, z // R0 = R0 + z
ST x, R0      // x = R0

利用特殊指令

对于 a = a + 1 这样的语句，通用翻译可能是：

1
2
3

LD R0, a      // R0 = a
ADD R0, R0, #1 // R0 = R0 + 1
ST a, R0      // a = R0

如果目标机有专门的自增指令 INC，那么一条指令就足够了，代价更低：

INC a

这说明，一个好的代码生成器需要了解目标指令集的特性，并选择代价最低的指令序列。

上下文相关的优化

指令选择还应考虑上下文。考虑以下代码序列：

1 2	a = b + c d = a + e

一个独立的、逐句翻译的方法会生成冗余代码：

// a = b + c
LD R0, b
ADD R0, R0, c
ST a, R0      // 将 a 的值存回内存

// d = a + e
LD R0, a      // 又从内存把 a 的值加载回来（冗余!）
ADD R0, R0, e
ST d, R0

如果代码生成器知道在计算 d = a + e 时，a 的值仍然在寄存器 R0 中，并且变量 a 在此之后不再被使用（即 a 是「死」的），就可以生成更优的代码：

LD R0, b
ADD R0, R0, c // 此时 R0 中是 a 的值
ADD R0, R0, e // 直接用 R0 中的值计算 d
ST d, R0      // 变量 a 从未被写回内存

这引出了「寄存器分配」和「活跃变量分析」的重要性。

地址管理

IR 中的名字（变量名、临时变量）必须被映射到目标代码中的地址。这个映射策略与第六章讨论的运行时环境密切相关。

静态分配下的过程调用

如果采用静态分配，编译器在编译时就能确定每个过程的活动记录在内存中的绝对地址。

调用 callee：
1. 将返回地址（call 指令的下一条指令地址）存入 callee 活动记录的预定位置。
2. 无条件跳转到 callee 的代码区入口。
1
2
ST callee.staticArea, #here+20 // 将返回地址（here+20）存入 callee 的 AR
BR callee.codeArea // 跳转到 callee
从 callee 返回：
1. 从 callee 的活动记录中取出返回地址。
2. 无条件跳转到该地址。
BR *callee.staticArea // 跳转到 AR 中保存的返回地址

静态分配的局限性

静态分配的主要问题是不支持递归。因为一个过程只有一个固定的活动记录，如果它调用自身，新的调用会覆盖旧的调用的返回地址和局部变量，导致程序无法正确返回和执行。

栈式分配下的过程调用

在支持递归的语言中，通常采用栈式分配。活动记录的地址在运行时才能确定，通常用一个专门的栈指针寄存器（Stack Pointer, SP）来指向当前栈顶。

调用 callee（由调用者 caller 执行）：

增加 SP，为 callee 的活动记录分配空间。
将返回地址压入栈中（存入新活动记录的预定位置）。
跳转到 callee。

1
2
3

ADD SP, SP, #caller.recordSize // SP 指向 caller 栈帧顶部
ST 0(SP), #here+16             // 将返回地址存入 callee 栈帧的开始位置
BR callee.codeArea             // 跳转

从 callee 返回：

被调用者 callee 执行跳转，返回到调用者 caller。

BR *0(SP)                      // 跳转到栈顶保存的返回地址

调用者 caller 回收栈空间。

SUB SP, SP, #caller.recordSize // 恢复 SP

基本块与流图

为了进行更有效的代码优化，我们不能再逐条地看待三地址指令。我们需要将它们组织成更大的逻辑单元。

基本块

基本块（Basic Block）是一段连续的三地址指令序列，它只有一个入口和一个出口。具体来说：

控制流只能从基本块的第一条指令（称为首指令或 leader）进入。
除了基本块的最后一条指令外，中间没有任何指令会导致跳转或停机。

一旦进入一个基本块，其中的所有指令都会按顺序执行完毕。

我们可以通过以下算法将一个三地址指令序列划分为基本块：

确定首指令：
- 程序的第一条指令是首指令。
- 任何一条跳转指令的目标指令是首指令。
- 任何一条紧跟在跳转指令之后的指令是首指令。
构造基本块：
- 每个首指令标志着一个新基本块的开始。
- 一个基本块从它的首指令开始，一直延伸到下一个首指令（不包括）之前，或者到程序结束。

基本块划分示例

考虑以下三地址码（行号代表指令位置）：

(1)  i = 1
(2)  j = 1
(3)  t1 = 10 * i
(4)  t2 = t1 + j
(5)  t3 = 8 * t2
(6)  t4 = t3 - 88
(7)  a[t4] = 0.0
(8)  j = j + 1
(9)  if j <= 10 goto (3)
(10) i = i + 1
(11) if i <= 10 goto (2)
(12) i = 1
(13) t5 = i - 1
(14) t6 = 88 * t5
(15) a[t6] = 1.0
(16) i = i + 1
(17) if i <= 10 goto (13)

确定首指令：

(1) 是程序的第一条指令。
(3) 是 goto (3) 的目标。
(2) 是 goto (2) 的目标。
(13) 是 goto (13) 的目标。
(10) 紧跟在 goto (3) 之后。
(12) 紧跟在 goto (2) 之后。

所以，首指令是 (1), (2), (3), (10), (12), (13)。

构造基本块：

B1: (1)
B2: (2)
B3: (3) - (9)
B4: (10) - (11)
B5: (12)
B6: (13) - (17)

流图

基本块之间的控制流关系可以用一个流图（Flow Graph）来表示。

节点：流图的节点是基本块。
边：如果基本块 B1 的最后一条指令可能跳转到 B2 的第一条指令，或者 B2 紧跟在 B1 之后且 B1 的结尾不是无条件跳转，那么就有一条从 B1 到 B2 的有向边。
B1 称为 B2 的前驱（predecessor），B2 称为 B1 的后继（successor）。
通常还会增加一个唯一的入口（ENTRY）节点和出口（EXIT）节点。

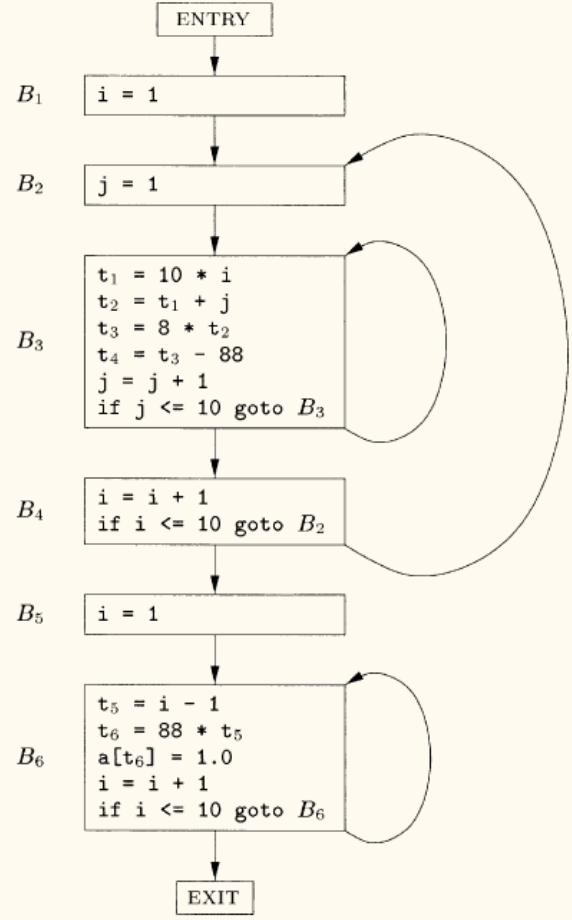
流图中的一个循环（Loop）是指从某个基本块 B 出发，经过一系列基本块后又回到 B 的路径（结点集合）。循环通常有一个循环入口（loop entry），是循环中唯一的前驱可以在循环外部的基本块。

上图中的循环有：

{B3}
{B6}
{B2, B3, B4}：其中 B2 为循环入口。

后续使用与活跃变量分析

流图为我们提供了进行数据流分析（Data-Flow Analysis）的基础，其中最重要的一种是活跃变量分析（Liveness Analysis）。

活跃变量（Live Variable）

使用（use）：如果语句 j 的一个操作数是 x，并且存在一条从语句 i（i 为 x 赋值）到 j 的路径，且路径上没有其他对 x 的赋值，我们就说 j 使用了在 i 处计算的 x 的值。
活跃（live）：在程序的某个点 p，如果变量 x 的当前值在从 p 开始的某条路径上可能被使用，那么我们称 x 在点 p 是活跃的。反之，如果 x 的值在未来不会被使用，则称其为不活跃的或死的（dead）。

活跃性信息对于寄存器分配和死代码消除至关重要。例如，如果一个变量在一个寄存器中，但在它被重新赋值之前，它在所有后续路径上都是死的，那么这个寄存器就可以被立即释放给其他变量使用。

计算基本块内的活跃性：我们可以通过从基本块的末尾向前扫描来确定每个语句执行前各变量的活跃性和后续使用信息。
假设我们知道在块的出口处哪些变量是活跃的。对于块中的一条指令 i: x = y op z：

记录 x, y, z 在指令 i 之前的活跃性信息。
将 x 的状态设置为「不活跃」（因为它将被重新定义），且无后续使用。
将 y 和 z 的状态设置为「活跃」，并记录它们的下一次使用就是指令 i。

这个过程从后向前迭代，直到块的入口。

示例

假设有以下基本块：

(1) a = 1
(2) b = a + 2
(3) a = b * 3
(4) c = a - b

来计算每一条指令执行前的活跃变量集合。

假设在基本块执行完毕后，只有变量 c 是活跃的（即它的值将在后续代码中被使用）。

分析过程（从后向前扫描）

分析指令 (4)：c = a - b
- 处理前：块出口处的活跃变量为 {c}。
- 应用规则:
  - c 被赋值，变为不活跃。
  - a 和 b 被使用，变为活跃。
- 处理后：指令 (4) 执行前的活跃变量为 {a, b}。
分析指令 (3)：a = b * 3
- 处理前：已知活跃变量为 {a, b}。
- 应用规则:
  - a 被赋值，变为不活跃。
  - b 被使用，变为活跃。
- 处理后：指令 (3) 执行前的活跃变量为 {b}。（集合 {a, b} 中去掉 a，加入 b，结果为 {b}）
分析指令 (2)：b = a + 2
- 处理前：已知活跃变量为 {b}。
- 应用规则:
  - b 被赋值，变为不活跃。
  - a 被使用，变为活跃。
- 处理后：指令 (2) 执行前的活跃变量为 {a}。
分析指令 (1)：a = 1
- 处理前：已知活跃变量为 {a}。
- 应用规则:
  - a 被赋值，变为不活跃。
  - 右侧没有使用变量。
- 处理后：指令 (1) 执行前（即基本块入口处）的活跃变量为 {} (空集)。

将活跃变量信息标注在代码中，结果如下：

// 入口处活跃：{}
(1) a = 1
// 此处活跃：{a}
(2) b = a + 2
// 此处活跃：{b}
(3) a = b * 3
// 此处活跃：{a, b}
(4) c = a - b
// 出口处活跃：{c}

这个从后向前的扫描精确地计算出了在每个程序点（即每条指令之前）的活跃变量集合。

基本块的 DAG 表示与优化

在基本块内部，我们可以使用有向无环图（Directed Acyclic Graph, DAG）来更紧凑地表示计算过程，并在此基础上进行局部优化。

用 DAG 表示基本块

一个基本块的 DAG 包含以下节点：

叶子节点：代表变量或常数的初始值。
内部节点：代表一个运算符，其子节点是参与运算的操作数。
节点上可以附加一个或多个变量名，表示该变量的当前值是由这个节点代表的计算结果所定义的。

构造算法：

为基本块中出现的每个变量创建初始值叶子节点。
顺序扫描基本块中的每条三地址指令：
- 对于指令 x = y op z：
  1. 找到 y 和 z 当前关联的节点 N_y 和 N_z。
  2. 查找：是否存在一个标号为 op 且子节点为 N_y 和 N_z 的节点 M？
  3. 如果存在（公共子表达式），则将变量 x 关联到现有的节点 M 上。
  4. 如果不存在，则创建一个新节点 N，标号为 op，子节点为 N_y 和 N_z，然后将 x 关联到这个新节点 N。
- 对于指令 x = y：
  1. 找到 y 当前关联的节点 N_y。
  2. 将 x 也关联到 N_y 上。

DAG 构造

考虑指令序列：

a = b + c
b = a - d
c = b + c
d = a - d

DAG 的构造过程如下：

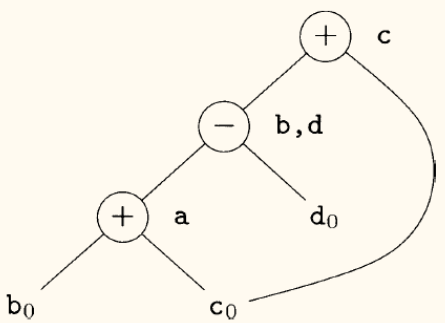
a = b + c: 创建 + 节点，子节点为 b0, c0。a 关联到此节点。
b = a - d: 创建 - 节点，子节点为 a 关联的 + 节点和 d0。b 关联到此新节点。
c = b + c: 创建新的 + 节点，子节点为 b 关联的 - 节点和 c0。c 关联到此节点。
d = a - d: 查找发现，已经存在一个 - 节点，其子节点是 a 关联的 + 节点和 d0。这是一个「公共子表达式」。因此，不再创建新节点，直接将 d 也关联到这个现有的 - 节点上。

基于 DAG 的局部优化

DAG 结构清晰地揭示了基本块内的计算依赖关系，使多种局部优化变得容易实现。

消除局部公共子表达式：在 DAG 构造过程中，如果发现要创建的节点已经存在，就复用它。这自然地消除了重复计算。在上面的例子中，a - d 被计算了一次，但其结果被赋给了 b 和 d。
消除死代码：在 DAG 构建完成后，如果一个根节点（没有父节点的节点）上关联的变量在基本块出口处都是不活跃的，那么这个节点对应的计算就是死代码，可以被消除。
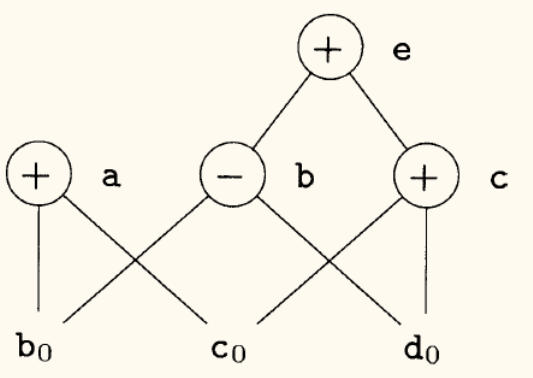
- 在上图中，若 c, e 不是活跃变量，则可以删除标号为 c, e 的结点。
应用代数恒等式：可以在 DAG 上寻找特定的模式，并用更简单的计算替换它们。
- 强度削弱（Strength Reduction）：x * 2 -> x + x
- 代数化简：x + 0 -> x，x * 1 -> x
- 常量合并（Constant Folding）：如果一个节点的子节点都是常量，可以在编译时直接计算出结果，用一个新的常量节点替换它。例如，节点 * 的子节点是 2 和 3.14，可以被替换为常量节点 6.28。
语句重排：DAG 表示的是数据依赖关系，而不是原始的语句顺序。只要不违反 DAG 中的依赖边，我们可以重新安排指令的顺序，这对于指令调度和优化非常有用。

DAG 表示的特殊情况

在基本块的 DAG 表示中，数组、指针和过程调用需要特殊处理，因为它们引入了别名（aliasing）和副作用（side effects），使得优化变得复杂。编译器必须做出保守的假设来保证程序的正确性。

数组引用

考虑以下代码序列：

1
2
3

x = a[i];
a[j] = y;
z = a[i];

一个直观但错误的优化是认为 a[i] 是一个公共子表达式，从而将 z = a[i] 替换为 z = x。

数组赋值的挑战

问题在于，编译器在编译时通常无法确定 i 和 j 的值是否相等。如果 i == j，那么 a[j] = y 这条语句会改变 a[i] 的值，导致 x 和第二次读取的 a[i] 的值不同。因此，我们不能将 a[i] 视为公共子表达式。

为了在 DAG 中正确地表示这种情况，我们将数组操作视为特殊的运算符：

数组取值 x = a[i]：对应一个标号为 =[] 的节点。该节点有两个子节点，分别代表数组的基地址（或其初始状态 a0）和下标 i。变量 x 会被附加到这个节点上。
数组赋值 a[j] = y：对应一个标号为 []= 的节点。该节点有三个子节点，分别代表数组基地址 a0、下标 j 和要赋的值 y。
- 这个节点本身不关联任何变量，因为它代表一个动作而非一个值。
- 最重要的是，这个节点会杀死（kill）所有依赖于 a 初始状态 a0 的节点。这意味着，在 a[j] = y 之后，任何之前从 a 中读取的值都变得无效。

graph TB
    subgraph "数组操作 DAG 表示"
        %% 初始状态节点
        a0(a0: 数组初始状态):::array
        i0(i0: 下标):::index
        j0(j0: 下标):::index
        y0(y0: 赋值数值):::value
        
        %% 数组取值操作
        N1["=[]<br/>数组取值（1）"]:::readOp
        a0 --> N1
        i0 --> N1
        N1 -- "定义变量 x" --> N_x((x)):::variable
        
        %% 数组赋值操作
        N2["[]=<br/>数组赋值（2）"]:::writeOp
        a0 --> N2
        j0 --> N2
        y0 --> N2
        
        %% 后续数组取值操作
        N3["=[]<br/>数组取值（3）"]:::readOp
        a0 --> N3
        i0 --> N3
        N3 -- "定义变量 z" --> N_z((z)):::variable
        
        %% 数据依赖关系
        N2 -. "杀死依赖关系<br/>（kill）" .-> N1:::killed
    end

    %% 样式定义
    classDef array fill:#e1f5fe,stroke:#01579b,stroke-width:2px
    classDef index fill:#f3e5f5,stroke:#4a148c,stroke-width:2px
    classDef value fill:#e8f5e8,stroke:#1b5e20,stroke-width:2px
    classDef readOp fill:#fff3e0,stroke:#e65100,stroke-width:2px
    classDef writeOp fill:#ffebee,stroke:#c62828,stroke-width:2px
    classDef variable fill:#fafafa,stroke:#424242,stroke-width:2px
    classDef killed fill:#f5f5f5,stroke:#9e9e9e,stroke-width:1px,stroke-dasharray: 3 3
    
    %% 链接样式
    linkStyle 9 stroke:#d32f2f,stroke-width:3px,stroke-dasharray: 5 5
    linkStyle 0,1,3,4,5,6,7 stroke:#757575,stroke-width:2px
    linkStyle 2,8 stroke:#1976d2,stroke-width:2px

在上图中，a[j]=y 对应的 []= 节点杀死（红色虚线）了 x=a[i] 对应的 =[] 节点（灰底）。因此，在构造 z=a[i] 的节点时，我们不能复用 N1，而必须重新创建一个从 a0 和 i0 出发的新节点 N3。

指针赋值与过程调用

指针和过程调用带来的不确定性更大。

指针赋值：
- x = *p（解引用读取）：编译器无法确定 p 指向何处，它可能指向任何变量。因此，这个操作依赖于之前所有的内存写操作。
- *q = y（解引用写入）：这是最棘手的情况。编译器必须假设这个操作可能修改任何变量。在 DAG 中，一个 *q = y 操作会杀死所有其他节点，因为这些节点代表的值可能已经被这次赋值所改变。
过程调用：
- 一个过程调用 call callee 同样是一个「黑盒」。它可能读取或修改任何全局变量，或者通过指针参数修改调用者环境中的变量。因此，过程调用也必须被保守地处理，通常会杀死所有可能被该过程影响的变量所对应的节点。

指针分析

这种「杀死所有节点」的策略过于保守，会限制很多优化机会。现代编译器通过指针分析（Pointer Analysis）等更复杂的技术来推断指针可能指向的内存位置集合，从而更精确地确定哪些节点需要被杀死。

C 语言中的严格别名规则

为了缓解指针赋值导致「杀死所有节点」的保守性，C/C++ 标准引入了严格别名规则（Strict Aliasing）。编译器可以依据此规则做出更激进的优化假设。

规则核心

编译器可以假设不同类型的指针（及其引用的对象）不会指向同一个内存地址。

例如，如果有一个 int* 指针和一个 float* 指针，编译器可以认为向 float* 写入数据绝对不会改变 int* 指向的内存中的值。

在构建 DAG 时，如果我们知道指针 p 是 int* 类型，而指针 q 是 float* 类型，那么语句 *q = y 对应的 *= 节点，就不需要杀死由 x = *p 产生的节点。

void strict_aliasing_demo(int *p, float *q) {
    x = *p;  // 节点 N1
   *q = 2.0; // 节点 N2
    z = *p;  // 节点 N3
}

不开启严格别名（保守策略）：*q = 2.0 可能修改 *p。N2 杀死 N1。N3 必须重新从内存读取。
开启严格别名（优化策略）：int 和 float 不兼容。N2 不会影响 N1。N3 可以直接复用 N1 的结果（即 z = x）。

graph TB
    subgraph "严格别名规则下的 DAG 优化"
        %% 初始状态节点
        p0(p0: int* 指针):::pointer
        q0(q0: float* 指针):::pointer
        y0(y0: 赋值数值 2.0):::value
        
        %% 指针解引用读取操作
        N1["*<br/>解引用读取（1）"]:::readOp
        p0 --> N1
        N1 -- "定义变量 x" --> N_x((x)):::variable
        
        %% 指针解引用赋值操作
        N2["*=<br/>解引用赋值（2）"]:::writeOp
        q0 --> N2
        y0 --> N2
        
        %% 后续指针解引用读取操作 - 可复用 N1
        N3["*<br/>解引用读取（3）"]:::readOp
        p0 --> N3
        N3 -- "定义变量 z" --> N_z((z)):::variable
        
        %% 数据依赖关系 - 严格别名允许复用
        N_x --> N3
        
        %% 严格别名保护说明
        StrictAlias(["严格别名规则保护<br/>int* 与 float* 类型不兼容"]):::aliasRule
        StrictAlias -.-> N1
        StrictAlias -.-> N2
    end

    %% 样式定义
    classDef pointer fill:#e8f5e8,stroke:#2e7d32,stroke-width:2px
    classDef value fill:#fff3e0,stroke:#ef6c00,stroke-width:2px
    classDef readOp fill:#e3f2fd,stroke:#1565c0,stroke-width:2px
    classDef writeOp fill:#fce4ec,stroke:#c2185b,stroke-width:2px
    classDef variable fill:#fafafa,stroke:#424242,stroke-width:2px
    classDef aliasRule fill:#f3e5f5,stroke:#7b1fa2,stroke-width:2px,dashed
    
    %% 链接样式
    linkStyle 0,2,3,4 stroke:#757575,stroke-width:2px
    linkStyle 1,5 stroke:#1976d2,stroke-width:2px
    linkStyle 6 stroke:#43a047,stroke-width:3px
    linkStyle 7,8 stroke:#7b1fa2,stroke-width:2px,stroke-dasharray: 3 3

例外情况：char*

严格别名规则有一个著名的例外：char*（以及 unsigned char*）可以指向任何类型。

这意味着，如果上述代码中 q 的类型是 char*，编译器必须回退到保守假设：*q = y 可能会修改 *p 的值，因此必须杀死相关节点。

类型双关（Type Punning）的风险

如果程序员通过强制类型转换违反了严格别名规则（例如将 int* 强转为 float* 并解引用），编译器的优化可能会导致生成的代码出现逻辑错误。这在 C 标准中属于未定义行为（Undefined Behavior, UB）。

从 DAG 重构基本块

在通过 DAG 进行了消除公共子表达式、死代码删除等优化后，我们需要将 DAG 转换回一个线性的三地址指令序列。由于 DAG 只表示数据依赖关系，我们可以有多种合法的指令顺序。

重构原则：

为 DAG 中的每个节点生成一条计算指令。
指令的顺序必须遵循 DAG 的拓扑排序，即一个节点的计算指令必须在其所有子节点的计算指令之后。
优先为活跃变量赋值：当一个节点的结果需要赋给一个变量时，应优先选择在基本块出口处活跃的变量。这可以避免后续不必要的 MOV 或 ST 指令。
处理多变量关联：如果一个节点关联了多个变量（例如，b 和 d 都等于 a - d），则先为其中一个变量（如 d）生成计算指令 d = a - d，然后为其他变量生成复制指令 b = d。

重构示例

考虑之前的 DAG 示例，原始代码为：

a = b + c
b = a - d
c = b + c
d = a - d

情况 1：只有 c 和 d 在出口处活跃。b 在出口不活跃，所以我们没有动机去保留 b 的值。a-d 的计算结果可以直接赋给 d。
1
2
3
a = b + c // 对应最左边的 '+' 节点
d = a - d // 对应 '-' 节点，结果赋给活跃的 d
c = d + c // 对应最顶部的 '+' 节点，注意操作数是 d
这个序列比原始代码少一条指令。

情况 2：b, c, d 都在出口处活跃。我们需要同时保留 b 和 d 的值，它们都等于 a-d。

a = b + c
d = a - d   // 计算公共子表达式，赋给 d
b = d       // 通过复制指令为 b 赋值
c = d + c   // c 的计算依赖于 a - d 的值，现在是 d

这个序列通过复用计算结果，避免了重复计算 a - d。

一个简单的代码生成算法

现在我们来讨论一个更具体的、基于基本块的代码生成算法。这个算法的核心目标是智能地利用寄存器，以最大限度地减少与内存之间的数据交换（即 LD 和 ST 指令）。

核心思想与数据结构

算法在遍历基本块的三地址指令时，需要实时追踪变量值和寄存器的状态。为此，我们使用两个关键的数据结构：

寄存器描述符（Register Descriptor）：一个映射，记录每个寄存器当前存放了哪些变量的值。一个寄存器可能存放多个变量的值（例如，在执行 x = y 后，如果 y 还在寄存器 R 中，那么 R 同时存放了 x 和 y 的值）。
地址描述符（Address Descriptor）：一个映射，记录每个变量的当前值存放在哪个或哪些位置。一个变量的值可能同时存在于内存和多个寄存器中。

算法框架

算法逐条处理三地址指令 I，并为之生成机器码。核心是 getReg(I) 函数，它为指令 I 的操作数和结果选择最合适的寄存器。

`getReg(I)` 函数：寄存器选择策略

getReg 函数是整个算法的「大脑」。当需要为变量 y（作为操作数）或 x（作为结果）寻找一个寄存器 R 时，它按以下顺序决策：

寻找 y 的寄存器（对于 x = y op z 中的 y）：
- 情况 A（最佳）：如果 y 的值已经在某个寄存器 R 中（查询地址描述符），直接选择 R。
- 情况 B（次佳）：如果情况 A 不满足，但有空闲的寄存器 R_free，则选择 R_free，并生成 LD R_free, y 指令。
- 情况 C（最差，需要溢出）：如果没有空闲寄存器，必须选择一个已被占用的寄存器 R_victim 来腾出（spill）。
  - 选择 R_victim：选择 R_victim 的启发式策略很重要。一个好的策略是选择一个持有的变量 v 满足以下条件之一的寄存器：
    1. v 的值在内存中也有备份（地址描述符表明 v 不仅在 R_victim 中）。
    2. v 在当前指令后不再被使用（v 是死的）。
    3. v 是当前指令的结果 x，且 x 不是操作数（因为 v 马上要被覆盖）。
  - 执行溢出：如果 v 在被覆盖后还需要使用，并且其当前值仅在 R_victim 中，则必须先生成 ST v, R_victim 将其保存回内存。
  - 加载 y：现在 R_victim 空闲了，生成 LD R_victim, y。
寻找 x 的寄存器（对于 x = y op z 的结果 x）：
- 选择逻辑与寻找 y 的寄存器类似。
- 一个重要的优化：如果操作数 y 所在的寄存器 Ry 在本条指令后不再持有任何活跃变量的值（特别是 y 本身不再使用），那么 Ry 是存放结果 x 的绝佳选择。这样可以避免分配新寄存器，并可能使 ADD Rx, Ry, Rz 变为 ADD Ry, Ry, Rz 这种更高效的二地址形式。

处理不同类型的指令

运算指令 x = y op z：
1. 调用 getReg 为 y 和 z 找到寄存器 Ry 和 Rz（可能需要生成 LD 指令）。
2. 调用 getReg 为 x 找到寄存器 Rx。
3. 生成指令 OP Rx, Ry, Rz。
4. 更新描述符：Rx 现在只存放 x；x 的位置只有 Rx（其内存值已过时）。
复制指令 x = y：
1. 调用 getReg 为 y 找到寄存器 Ry。
2. 更新描述符：将 x 也添加到 Ry 的寄存器描述符中，并将 x 的地址描述符设置为仅包含 Ry。不需要生成任何代码，实现了零成本赋值。
基本块结尾：
- 遍历所有在基本块出口处活跃的变量。
- 如果某个活跃变量 v 的最新值只在寄存器中（其内存副本已过时），则生成 ST v, R 将其写回内存，确保下一个基本块能获取到正确的值。

示例

假设有三地址码：

t = a - b
u = a - c
v = t + u
a = d
d = v + u

并且 a, b, c, d 在块出口处活跃（需要存回内存），t, u, v 是局部临时变量（出口处死亡），有三个可用寄存器：R1, R2, R3。

三地址指令	生成代码	寄存器描述符 `(R1, R2, R3)`	地址描述符（变量 `->` 位置）	备注与分析
（初始状态）	-	`(empty, empty, empty)`	`a:mem`; `b:mem`; `c:mem`; `d:mem`	初始时所有变量仅在内存中。
`t = a - b`	`LD R1, a`	`(a, empty, empty)`	`a:mem,R1`…	加载 `a` 到 R1。
-	`LD R2, b`	`(a, b, empty)`	`a:mem,R1`; `b:mem,R2`…	加载 `b` 到 R2。
-	`SUB R2, R1, R2`	`(a, t, empty)`	`a:mem,R1`; `b:mem`; `t:R2`	寄存器重用：计算结果 `t` 存入 R2。此时 `b` 的值在 `R2` 中被覆盖，但因为 `b` 在内存有备份且本指令后暂不使用，所以 `R2` 被选中。
`u = a - c`	`LD R3, c`	`(a, t, c)`	`a:mem,R1`; `c:mem,R3`…	加载 `c` 到 `R3`。
-	`SUB R1, R1, R3`	`(u, t, c)`	`u:R1`; `a:mem`; `t:R2`…	覆盖活跃变量：`u` 存入 `R1`。虽然 `a` 是 `R1` 原有的值且在出口活跃，但在此指令后 `a` 的值不再被引用（直到第 4 步 `a=d` 被重新赋值），因此原 `a` 的值此时是「死」的，`R1` 可以安全地被 `u` 覆盖。
`v = t + u`	`ADD R3, R2, R1`	`(u, t, v)`	`v:R3`; `u:R1`; `t:R2`	结果 `v` 存入 `R3`。`R3` 原有的 `c` 被覆盖（`c` 在内存有值）。此时 `R1`(`u`) 和 `R2`(`t`) 依然被占用。
`a = d`	`LD R2, d`	`(u, a/d, v)`	`a:R2`; `d:mem,R2`; `u:R1`…	寻找空闲：需要加载 `d`。查看寄存器，`t`（在 `R2`）在本指令后不再活跃，因此 `R2` 被释放并用于加载 `d`。由于是赋值操作，`a` 和 `d` 现在都映射到 `R2`。
`d = v + u`	`ADD R1, R3, R1`	`(d, a, v)`	`d:R1`; `a:R2`; `v:R3`; `u:mem`	结果覆盖操作数：计算 `v+u`。操作数 `u`（在 `R1`）在此使用后死亡，因此 `R1` 被选作目标寄存器存放结果 `d`。注意此时 `R2` 中存放的是 `a` 的值（即旧的 `d`），而 `R1` 中是最新的 `d`。
（出口 Exit）	`ST a, R2`	`(d, a, v)`	`a:mem,R2`…	写回活跃变量：`a` 在 `R2` 中是脏数据（只有寄存器有新值），且在出口活跃，生成 `ST` 指令。
-	`ST d, R1`	`(d, a, v)`	`d:mem,R1`…	写回活跃变量：`d` 在 `R1` 中是脏数据，且在出口活跃，生成 `ST` 指令。`v` 虽然在 `R3` 但它是临时变量，无需写回。

窥孔优化

窥孔优化（Peephole Optimization）是一种简单而有效的局部优化技术。它在代码生成之后（或期间）进行，通过一个小的、滑动窗口（即「窥孔」）来检查目标指令序列，寻找并替换已知的低效指令模式。

常见窥孔优化类型：

冗余指令消除：
- 冗余加载/存储：ST R, x 后紧跟着 LD R, x，如果中间没有对 x 的修改或跳转到 LD 指令，那么 LD 指令是多余的，可以删除。
- 不可达代码：在无条件跳转指令 BR L1 之后，直到下一个标号 L2: 之前的代码都是不可达的，可以删除。
控制流优化：
- 跳转到跳转：BR L1 … L1: BR L2 可以被优化为 BR L2 … L1: BR L2。
- 跳转到下一条指令：BR L1 … L1: <下一条指令> 可以直接删除 BR L1。
代数化简与强度削弱：
- 代数恒等式：x = x + 0 或 x = x * 1 这样的指令可以被删除。
- 强度削弱：将代价高的运算替换为代价低的运算。例如整数运算 x = x * 2 可以替换为 x = x << 1（左移一位），x = x/2 替换为 x = x >> 1（算术右移一位）。
利用机器特有指令：
- 许多处理器提供特殊的指令来完成常见操作。例如，ADD R, R, #1 可以被替换为更短、更快的 INC R（自增）指令。

全局寄存器分配

前面讨论的算法是针对单个基本块的。当程序的控制流跨越多个基本块时，尤其是在循环中，我们需要一种全局寄存器分配（Global Register Allocation）策略。

基本块代码生成的隐含假设：

变量使用前必须先加载到寄存器中（LD）。
活跃变量在基本块结束时必须存回内存（ST）。

其核心思想是，将那些在程序（特别是循环）中被频繁访问的变量，在整个生命周期内都分配一个固定的寄存器。

基于使用计数的分配策略

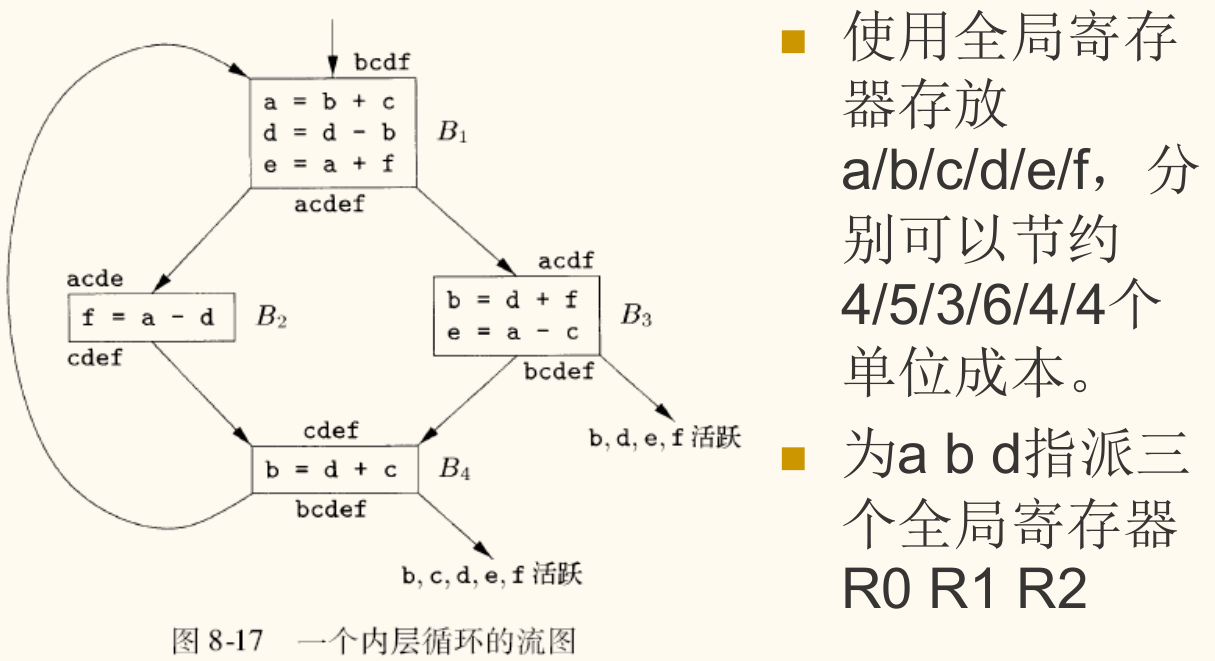
一个简单的全局分配启发式方法是基于使用计数。我们可以估算将一个变量 $x$ 放入寄存器能带来的「收益」。对于一个循环 $L$ ，这个收益可以近似为：

$\operatorname{Benefit}(x) = \sum_{B \in L} \left[ \operatorname{use}(x, B) + 2 \times \operatorname{live}(x, B) \right]$

其中 $B$ 表示循环中的每个基本块。

$\operatorname{use}(x, B)$ ：变量 $x$ 在块 $B$ 中被定值之前的使用次数。每次使用可以节省一次 LD 指令（代价为 1）。
$\operatorname{live}(x, B)$ ：如果 $x$ 在块 $B$ 中被定值，并且在 $B$ 的出口处是活跃的，则 $\operatorname{live}(x, B)$ 为 1，否则为 0。这表示我们可以省去一次在块末尾的 ST 指令（代价通常比 LD 高，这里计为 2）。

通过为每个变量计算这个收益值，我们可以优先将收益最高的变量分配给可用的全局寄存器。

基于树重写的指令选择

树重写（Tree Rewriting）是一种更形式化和强大的指令选择技术。它将中间表示（如三地址码）转换为树形结构，然后通过一组重写规则（rewriting rules）来匹配树的模式，并将其替换为目标机指令。

表示：将 IR 表达式表示为语法树。
匹配：每条目标机指令对应一个或多个树模式（template）。
覆盖：算法的目标是找到一组树模式，以最低的总代价覆盖整个 IR 树。

这个过程类似于用不同形状的瓷砖（指令）来铺满整个地板（IR 树）。这是一个复杂的最优覆盖问题，但可以使用动态规划或贪心算法来找到一个好的解。这种方法能够自然地处理具有复杂寻址模式的 CISC 指令集，生成非常紧凑和高效的代码。