机器无关的优化

发表于 2025-12-02 更新于 2025-12-16 Waline：阅读次数：本文字数： 8.3k 阅读时长 ≈ 30 分钟

优化的目标与分类

代码优化是编译器后端的一项关键技术，其目标是在不改变程序原始语义的前提下，对中间代码或目标代码进行等价变换，使其运行得更快、占用空间更少。一个优秀的优化器能够在编译时间、代码质量和工程复杂度之间取得良好的平衡。

graph LR
    A[📄 源程序] --> B{🔄 前端};
    B --> C[⚙️ 中间代码];
    C --> D[🚀 代码优化器];
    D --> E[(⚙️ 优化后中间代码)];
    E --> F{🎯 后端：代码生成器};
    F --> G[💻 目标程序];

    %% 样式定义
    classDef default fill:#f8f9fa,stroke:#495057,stroke-width:2px,color:#212529;
    classDef process fill:#e3f2fd,stroke:#1565c0,stroke-width:2px;
    classDef decision fill:#fff3e0,stroke:#ef6c00,stroke-width:2px;
    classDef output fill:#e8f5e8,stroke:#2e7d32,stroke-width:2px;

    %% 应用样式
    class A,G output;
    class B,F decision;
    class C,D,E process;

    %% 连接线样式
    linkStyle default stroke:#666,stroke-width:2px,fill:none;

本章我们关注的是机器无关的优化（Machine-Independent Optimization），这类优化作用于中间表示（如三地址码），不依赖于具体的目标机器架构（如 CPU 型号、寄存器数量等）。

根据优化的作用范围，我们还可以将其分为：

局部优化：仅在单个「基本块」内部进行的优化。
全局优化：跨越基本块边界，在整个过程（函数）的「流图」上进行的优化。

优化的主要来源与方法

优化的机会无处不在。有些源于程序员编写的冗余代码，但更多是高级语言特性在翻译为低级中间代码过程中的「副产品」。例如，数组的多维地址计算 A[i][j] 会被展开为一系列的乘法和加法，这其中就可能包含重复的计算。

以下是几种经典且相互关联的机器无关优化技术。

全局公共子表达式消除

全局公共子表达式

公共子表达式（Common Subexpression）是指在程序中多次出现且每次计算时其操作数的值都相同的表达式。

局部公共子表达式：在单个基本块内重复出现的表达式。
全局公共子表达式：在不同基本块中重复出现的表达式。

消除（Elimination）的基本思想是：计算一次表达式的值，将其保存在一个临时变量中，后续所有对该表达式的引用都替换为对这个临时变量的使用。

快速排序中的公共子表达式

在 quicksort 示例的流图中，首先基本块 B5 内就有重复计算 4*i 与 4*j（t7 与 t10）。

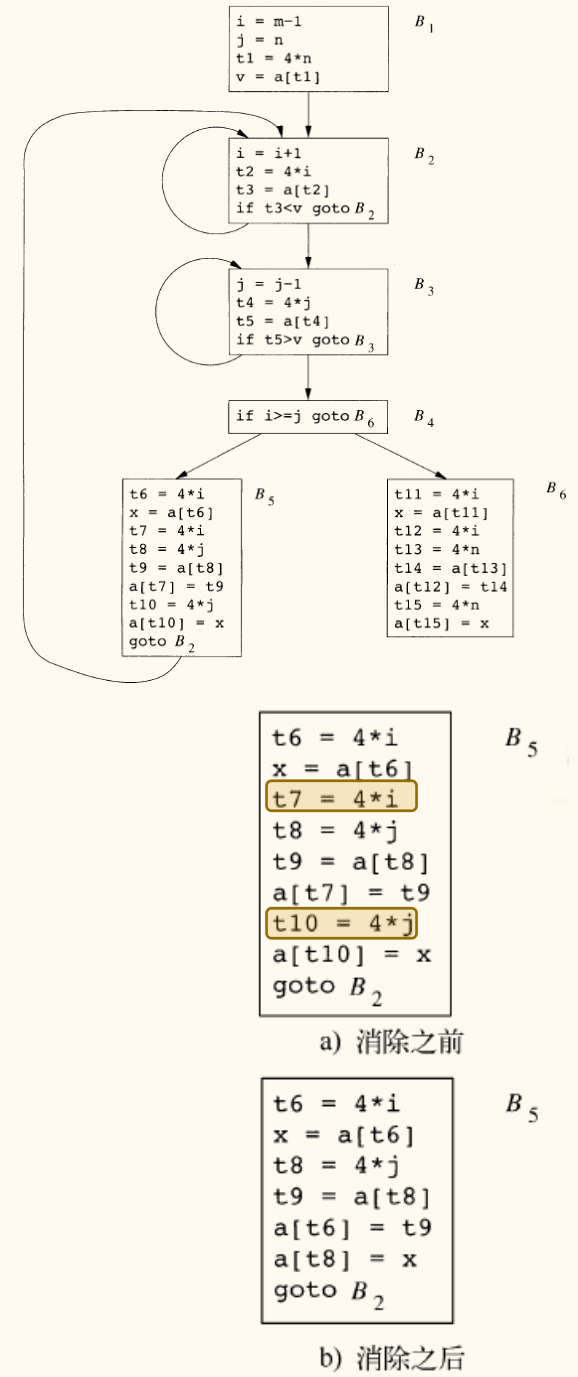
而此外如果我们能确定从 B2 到达 B5 的路径上 i 的值没有改变，那么 B2 中计算的 t2 = 4*i 的结果就还可以在 B5 中复用。

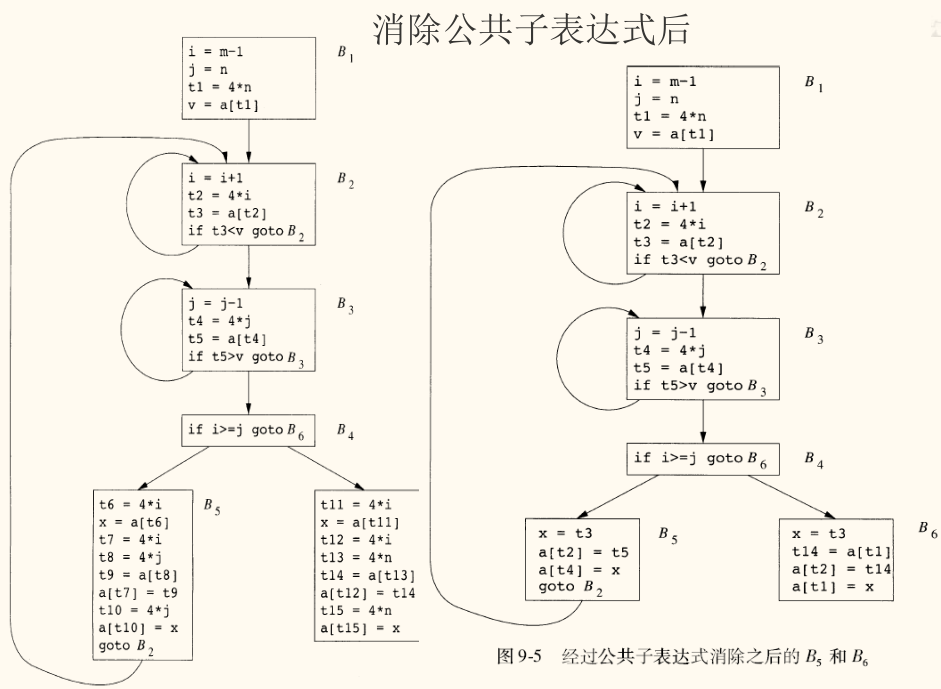
这种优化需要复杂的数据流分析来保证其正确性。

复制传播

复制传播（Copy Propagation）是指在执行了一条形如 u = v 的复制语句（Copy Statement）后，将后续代码中对 u 的使用替换为对 v 的使用。

这种优化本身可能不会直接提升性能，但它常常为其他优化（特别是死代码消除）创造条件。

graph LR
    subgraph "复制传播的作用"
        direction LR
        A["x = y + z<br/>a = x"] --> B["b = a * 2<br/>c = a + 1"];
        B -- "应用复制传播<br/>（用 x 替换 a）" --> C["b = x * 2<br/>c = x + 1<br/>（a = x 变为死代码）"];
        C -- "应用死代码消除" --> D["b = x * 2<br/>c = x + 1"];
    end

    classDef step fill:#e3f2fd,stroke:#1565c0;
    class A,B,C,D step;

在公共子表达式消除后，我们可能会引入新的复制语句，例如基本块 B5 中的 x = t3。复制传播可以将后续的 a[t4] = x 替换为 a[t4] = t3，这可能使得 x = t3 这条赋值语句变得无用。

死代码消除

死代码

死代码（Dead Code）是指程序的执行结果永远不会被使用的代码。最常见的死代码是对一个死变量（Dead Variable）的赋值。一个变量在某点是「死的」，如果从该点开始的任何执行路径上，它的当前值都不会再被读取。

死代码消除就是将这些无用的代码从程序中移除。它通常在其他优化（如复制传播）之后执行，扮演着「清道夫」的角色。

在 quicksort 示例中，经过复制传播后，B5 中的 x = t3 赋值给了 x，但 x 的值在被 a[t4] = t3 覆盖之前没有被任何地方使用，因此 x=t3 是一条死代码，可以被安全地删除。

代码移动（循环不变式外提）

循环不变表达式

循环不变表达式（Loop-Invariant Expression）是指在循环的多次迭代中，其计算结果始终保持不变的表达式。

代码移动（Code Motion），特别是循环不变式外提（Loop-Invariant Code Motion），是一种重要的优化。它将循环不变表达式的计算从循环体内移动到循环开始前（称为前置首结点，preheader）的位置。这样，原本需要重复计算多次的表达式现在只需计算一次，大大提高了循环的执行效率。

循环不变式外提

优化前：

1
2
3

while (i <= limit - 2) {
    // ... 循环体不修改 limit
}

在每次循环判断时，都会计算一次 limit - 2。

优化后：

t = limit - 2;
while (i <= t) {
    // ...
}

计算被移出循环，只执行一次。

归纳变量与强度削弱

归纳变量

在一个循环中，如果一个变量 i 的值每次迭代都只增加或减少一个常量（例如 i = i + c），那么 i 就是一个基本归纳变量（Basic Induction Variable）。

如果另一个变量 j 的值是 i 的线性函数（j = a * i + b），那么 j 也是一个归纳变量。

识别出归纳变量后，我们可以进行强度削弱（Strength Reduction）优化，即用计算代价更低的运算来替换代价高的运算。

对于归纳变量 j = a * i + b，当 i 变为 i + c 时，j 的新值是 a * (i + c) + b = (a * i + b) + a * c。这意味着，原本需要一次乘法和一次加法来计算 j，现在可以通过在 j 的旧值上增加一个常量 a * c 来得到。这样，我们就用一次加法替换了一次乘法。

归纳变量优化

在 quicksort 的内部 do-while 循环中（如 B3），j 是一个基本归纳变量（j = j - 1）。t4 = 4 * j 是一个归纳变量。

优化前（B3）:

L: j = j - 1
   t4 = 4 * j
   ...
   goto L

每次循环都有一次乘法。

优化后（B3）:
在进入循环前，计算 t4 = 4 * j。

L: j = j - 1
   t4 = t4 - 4  // 强度削弱：用减法代替乘法
   ...
   goto L

如果循环中不再需要 j 本身，我们甚至可以完全删除归纳变量 j，只保留 t4。

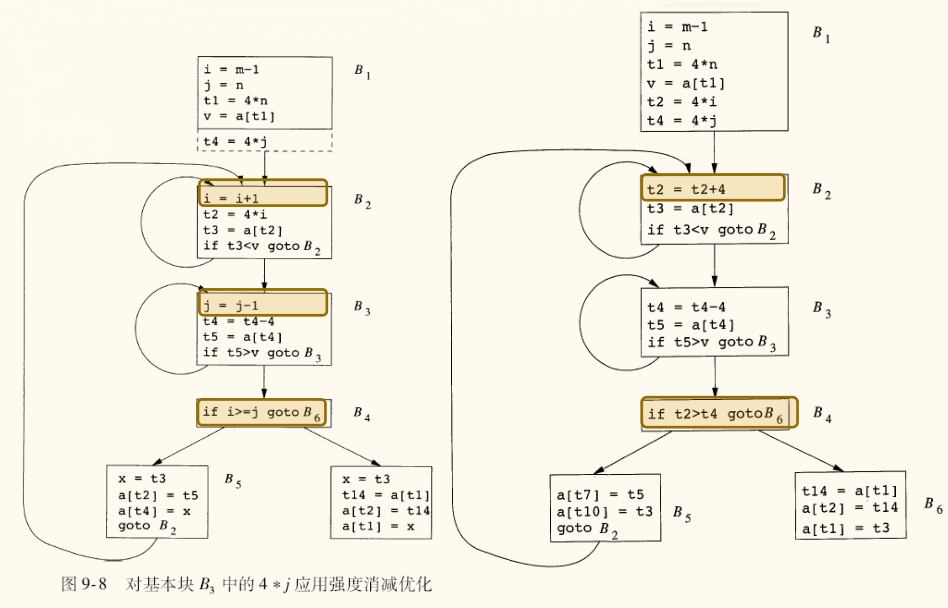
数据流分析：优化的理论基础

考试不考。

上述的全局优化（如全局公共子表达式消除、代码移动等）都需要精确地了解信息在程序中的流动情况。例如，要消除 x + y，我们必须确保从上一个计算点到当前点，x 和 y 的值都没有改变。数据流分析（Data-Flow Analysis）就是为解决这类问题而设计的理论框架。

核心概念：

程序点：程序中的一个位置，可以位于语句之前或之后。
程序状态：在某个运行时刻，当执行到达某个程序点时，所有变量和内存的值的快照。
数据流值，而是关心它们的某种性质。例如：
- 对于常量传播，数据流值可能是 { (x, 5), (y, NAC), (z, 10) }，表示 x 是常量 5，z 是常量 10，而 y 不是常量（Not-A-Constant）。
- 对于到达定值分析，数据流值是一个定值语句的集合。

数据流分析的本质是一种抽象解释（Abstract Interpretation）。它通过对程序的具体执行过程进行近似和抽象，来推断程序的性质。对比具体解释，通过对感兴趣的问题进行近似的抽象，取出其中的关键部分进行分析，从而使得程序内部的状态是有限的。

安全性（Safety）：分析得到的结果必须是一个安全的估计。例如，如果分析结果说变量 x 在某点是常量 5，那么在程序的任何实际执行中，当到达该点时 x 的值必须是 5。但反过来，即使 x 实际上总是 5，分析结果也可能保守地认为它不是常量。这种保守性保证了基于分析结果的优化不会改变程序语义。
有限性与单调性：为了保证分析算法能够在有限时间内结束，我们要求抽象的程序状态（数据流值）是有限的，并且在迭代分析过程中，状态的变化是单调的（例如，集合只增不减）。

数据流分析框架

一个具体的数据流分析问题可以被形式化为一个数据流分析框架 $(D, V, F, M)$ ，它由以下几个部分组成：

D: 方向（Direction）
- 前向分析：信息沿着控制流的方向传播。一个语句的 $\operatorname{OUT}$ 状态是根据其 $\operatorname{IN}$ 状态计算的。例如：到达定值分析。
- 后向分析：信息沿着控制流的反方向传播。一个语句的 $\operatorname{IN}$ 状态是根据其 $\operatorname{OUT}$ 状态计算的。例如：活跃变量分析。
V: 值域（Values）
- 数据流值的集合。通常是一个半格（Semilattice），定义了值的偏序关系。
M: 交汇运算（Meet/Confluence Operator）
- 用于合并来自多条控制流路径的信息。当一个基本块 $B$ 有多个前驱 $P1, P2, ...$ 时， $B$ 的入口状态 $\operatorname{IN}[B]$ 是通过对其所有前驱的出口状态 $\operatorname{OUT}[P1], \operatorname{OUT}[P2], ...$ 应用交汇运算得到的。
- $\operatorname{IN}[B] = M(\operatorname{OUT}[P1], \operatorname{OUT}[P2], ...)$
F: 传递函数族（Family of Transfer Functions）
- 每个语句 $s$ 或基本块 $B$ 都有一个传递函数 $f_s$ 或 $f_B$ 。它描述了该语句/基本块如何转换数据流信息。
- 对于前向分析： $\operatorname{OUT}[s] = f_s(\operatorname{IN}[s])$
- 对于后向分析： $\operatorname{IN}[s] = f_s(\operatorname{OUT}[s])$

May 分析与 Must 分析

根据交汇运算和我们关心的问题性质，数据流分析可以分为两类：

May 分析：用于分析在程序点上可能存在的性质。交汇运算通常是并集（ $\cup$ $\cup$ ）。
- 例子：到达定值分析。我们想知道哪些定值「可能」到达一个程序点。只要存在一条路径能让定值 $d$ 到达点 $p$ ，我们就认为 $d$ 到达了 $p$ 。
Must 分析：用于分析在程序点上一定存在的性质。交汇运算通常是交集（ $\cap$ $\cap$ ）。
- 例子：可用表达式分析。我们想知道哪些表达式在点 $p$ 「一定」是可用的（即在所有通往 $p$ 的路径上都被计算过，且其操作数未被修改）。

实例：到达定值分析

到达定值分析（Reaching Definitions Analysis）是最基础的数据流分析之一，用于确定在程序的每个点，变量的当前值可能是由哪些赋值语句（即定值）创建的。

到达定值

一个定值 d: u = v + w 到达（reaches）程序点 p，如果存在一条从 d 之后的点到 p 的路径，且该路径上没有其他对变量 u 的定值。

任何对 u 的新定值都会杀死（kill）之前所有关于 u 的定值。

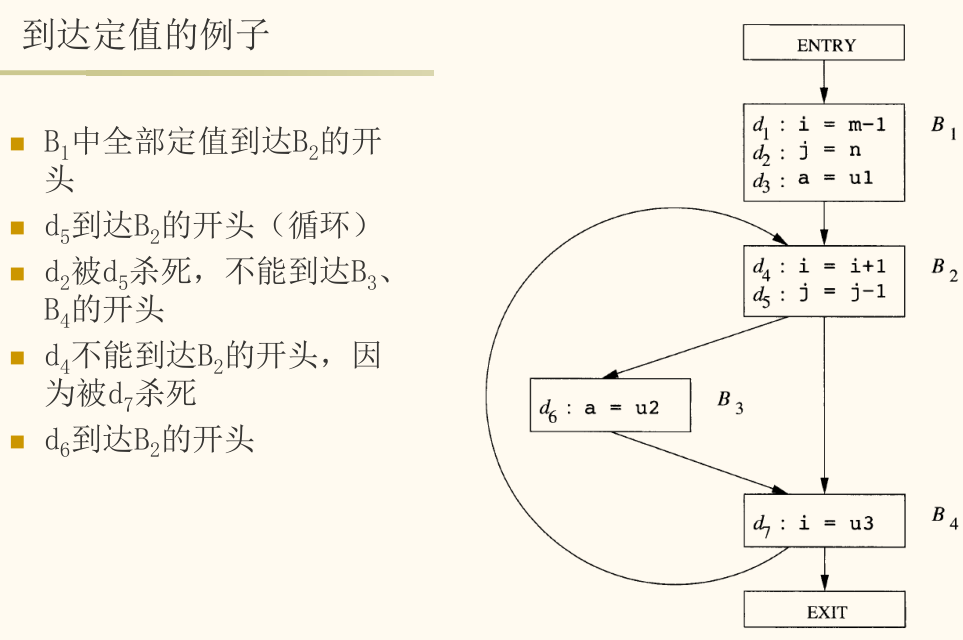
到达定值分析的结果构成了变量之间的定值-使用链（define-use chain, DU-chain），是许多优化的基础，如常量传播和循环不变代码外提。

到达定值分析的框架

D（方向）: 前向分析。
V（值域）: 程序中所有定值的集合的幂集 $P(\mathrm{Defs})$ 。通常用一个位向量（bitvector）表示，每一位对应一个定值。
M（交汇运算）: 并集（ $\cup$ ）。一个定值到达块 $B$ 的入口，只要它能从任何一个前驱块的出口到达。
F（传递函数）: 对于一个基本块 $B$ $B$ ，其传递函数 $f_B$ $f_{B}$ 可以用 $\mathrm{gen}$ $gen$ 和 $\mathrm{kill}$ $kill$ 集合来定义：
- $\mathrm{kill}[B]$ $kill [B]$ ：在块 $B$ $B$ 内部被杀死的（即被重新定义的变量的）来自程序其他地方的定值集合。
  - 是一个能力声明，表示只要基本块执行了，就会杀死这些定值，而不考虑控制流路径。
- $\mathrm{gen}[B]$ ：在块 $B$ 内部生成，并且能存活到块 $B$ 出口的定值集合。
- 传递方程为： $\operatorname{OUT}[B] = \mathrm{gen}[B] \cup (\operatorname{IN}[B] - \mathrm{kill}[B])$

综合以上要素，我们得到到达定值分析的两个核心数据流方程：

块内传递方程： $\operatorname{OUT}[B] = \mathrm{gen}[B] \cup (\operatorname{IN}[B] - \mathrm{kill}[B])$
块间汇集方程： $\operatorname{IN}[B] = \bigcup\limits_{P \in \operatorname{pred}(B)} \operatorname{OUT}[P]$ $IN [B] = P \in pred (B) ⋃ OUT [P]$
- 其中 $\operatorname{pred}(B)$ 是基本块 $B$ 的所有前驱块的集合。

迭代求解算法

这一组方程组可以通过一个迭代算法来求解，直到所有 $\operatorname{IN}$ 和 $\operatorname{OUT}$ 集合不再变化，达到一个不动点。

算法步骤:

初始化：
- $\operatorname{OUT}[\mathrm{ENTRY}] = \empty$
- 对所有其他基本块 $B$ ， $\operatorname{OUT}[B] = \empty$ 。
迭代：

$\begin{align*} &\mathbf{while}\ (\text{某个 } \operatorname{OUT}[B] \text{ 集合发生了改变}): \\ &\quad \mathbf{for} \ (\text{每个非 ENTRY 的基本块 } B): \\ &\qquad (1) \ \operatorname{IN}[B] = \bigcup_{P \in \operatorname{pred}(B)} \operatorname{OUT}[P] \\ &\qquad (2) \ \operatorname{OUT}[B] = \mathrm{gen}[B] \cup (\operatorname{IN}[B] - \mathrm{kill}[B]) \\ \end{align*}$

求解示例

以下是课件中例子的 $\mathrm{gen}/\mathrm{kill}$ 集和迭代求解过程的表格化表示。假设有 7 个定值 $d_1$ 到 $d_7$ ，我们用一个 7 位的向量表示定值集合。

定值	语句	变量
$d_1$	`i = m - 1`	`i`
$d_2$	`j = n`	`j`
$d_3$	`a = u1`	`a`
$d_4$	`i = i + 1`	`i`
$d_5$	`j = j - 1`	`j`
$d_6$	`a = u2`	`a`
$d_7$	`i = u3`	`i`

Gen/Kill 集:

$\mathrm{gen}[B1] = \{d_1, d_2, d_3\}$
$\mathrm{kill}[B1] = \{d_4, d_5, d_6, d_7\}$ （杀死程序中所有其他对 i, j, a 的定值）
$\mathrm{gen}[B2] = \{d_4, d_5\}$
$\mathrm{kill}[B2] = \{d_1, d_2, d_7\}$
$\mathrm{gen}[B3] = \{d_6\}$
$\mathrm{kill}[B3] = \{d_3\}$
$\mathrm{gen}[B4] = \{d_7\}$
$\mathrm{kill}[B4] = \{d_1, d_4\}$

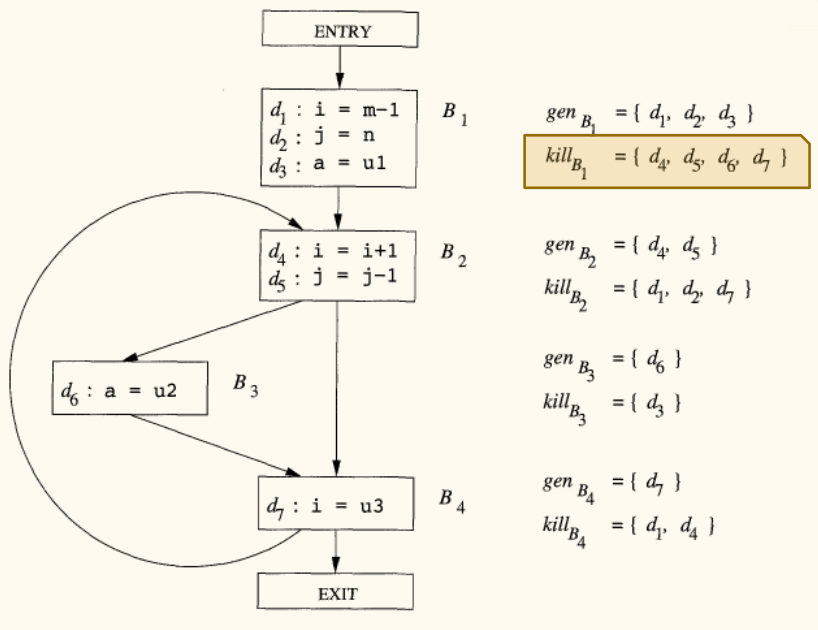
迭代过程（1 表示定值在集合中，0 表示不在）：每轮迭代按顺序依次遍历 B1, B2, B3, B4, EXIT。

Block	$\operatorname{OUT}[B]$ （初始）	$\operatorname{IN}[B]$ （迭代 1）	$\operatorname{OUT}[B]$ （迭代 1）	$\operatorname{IN}[B]$ （迭代 2）	$\operatorname{OUT}[B]$ （迭代 2）
B1	`000 0000`	`000 0000`	`111 0000`	`000 0000`	`111 0000`
B2	`000 0000`	`111 0000`	`001 1100`	`111 0110`	`001 1110`
B3	`000 0000`	`001 1100`	`000 1110`	`001 1110`	`000 1110`
B4	`000 0000`	`001 1110`	`001 0111`	`001 1110`	`001 0111`
EXIT	`000 0000`	`001 0111`	`001 0111`	`001 0111`	`001 0111`

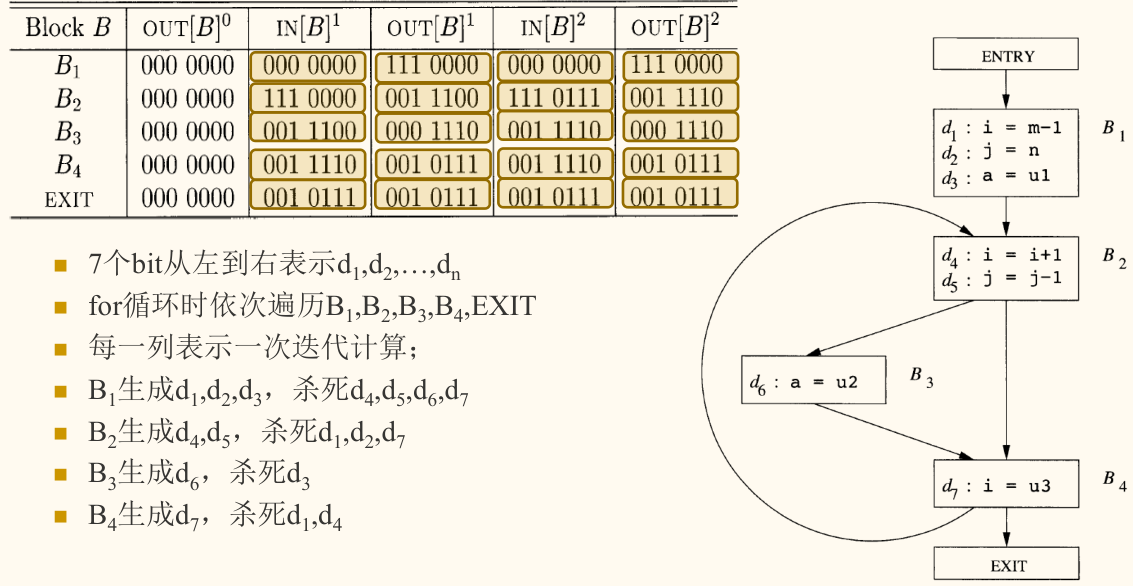
算法的终止性与正确性

终止性：在迭代过程中， $\operatorname{OUT}[B]$ 集合是单调递增的（只增不减）。由于定值的总数是有限的，所以集合的大小存在一个上界。因此，算法必然会在有限步内终止。
正确性：算法最终得到的是满足数据流方程的最小不动点解，这对应于最精确和安全的分析结果。

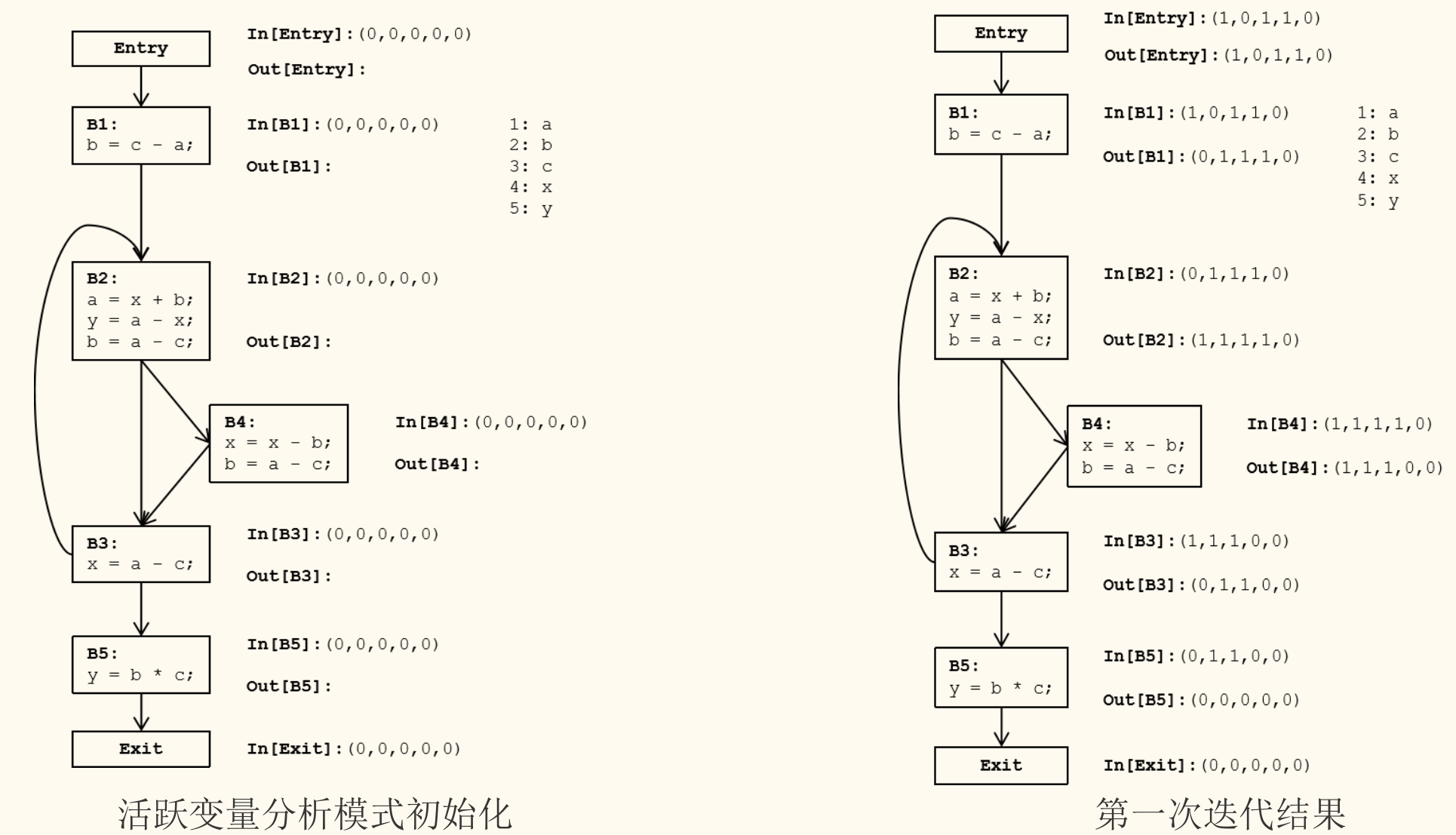
实例：活跃变量分析

与到达定值分析关注「过去」不同，活跃变量分析（Live Variable Analysis）关注的是「未来」。它试图回答：变量 x 在程序点 p 的值是否会在后续的执行路径中被使用？

活跃变量

如果存在一条从程序点 p 开始的路径，该路径的末端使用了变量 x，且在该路径上没有对 x 进行覆盖（即重新赋值），则称变量 x 在点 p 是活跃的（Live）。否则，称 x 是死的（Dead）。

主要用途：

寄存器分配：如果一个变量在某点之后不再活跃，它占用的寄存器就可以被释放或分配给其他变量。
死代码消除：如果一个变量赋值后立即变为死变量，那么这条赋值语句通常可以被删除。

活跃变量分析框架

活跃变量分析是一个后向的 May 分析。我们需要从程序的出口向入口反向传播信息。

D（方向）：后向。
V（值域）：变量的集合。
M（交汇运算）：并集（ $\cup$ ）。只要在任意一条后继路径上变量被使用，它就是活跃的。
F（传递函数）：
- $\operatorname{use}_B$ ：在基本块 $B$ 中被使用，且在使用前没有在 $B$ 中被重定义的变量集合（即 $B$ 需要从外部获取值的变量）。
- $\operatorname{def}_B$ ：在基本块 $B$ 中被定值（赋值）的变量集合（这些定值会「杀死」该变量之前的活跃状态）。

与到达定值分析类似，得到活跃变量分析的核心方程，但方向相反：

块内传递方程（逆向计算）：
$\operatorname{IN}[B] = \operatorname{use}_B \cup (\operatorname{OUT}[B] - \operatorname{def}_B)$
块间汇集方程：
$\operatorname{OUT}[B] = \bigcup_{S \in \operatorname{succ}(B)} \operatorname{IN}[S]$
其中 $\operatorname{succ}(B)$ 是 $B$ 的后继基本块集合。

注意方向

与到达定值不同，这里是从 $\operatorname{OUT}$ 计算 $\operatorname{IN}$ 。 $\operatorname{OUT}[B]$ 代表了紧接在 $B$ 之后活跃的变量，它们来源于 $B$ 的所有后继块的 $\operatorname{IN}$ 集合的并集。

迭代求解算法

活跃变量分析采用后向迭代算法求解。

算法步骤：

初始化：
- $\operatorname{IN}[\mathrm{EXIT}] = \empty$
- 对所有其他基本块 $B$ （除 EXIT 外）， $\operatorname{IN}[B] = \empty$ 。
迭代：

$\begin{align*} &\mathbf{while}\ (\text{某个 } \operatorname{IN} \text{ 值发生了改变}): \\ &\quad \mathbf{for} \ (\text{除 EXIT 之外的每个基本块 } B): \\ &\qquad (1) \ \operatorname{OUT}[B] = \bigcup_{S \in \operatorname{succ}(B)} \operatorname{IN}[S] \\ &\qquad (2) \ \operatorname{IN}[B] = \mathrm{use}_B \cup (\operatorname{OUT}[B] - \mathrm{def}_B) \\ \end{align*}$

算法的终止性

这个算法中 $\operatorname{IN}[B]$ 集合的大小总是越来越大（单调递增）。
且 $\operatorname{IN}[B]$ 都有上界（即程序中所有变量的集合）。
因此，算法必然会在有限步内终止。

实例：可用表达式分析

可用表达式分析（Available Expressions Analysis）用于判断一个表达式 x + y 是否已经计算过且无需重新计算。

可用表达式

如果从流图入口到达程序点 p 的每一条路径都对表达式 x + y 进行了求值，且在最后一次求值之后，x 和 y 都没有被重新赋值，则称表达式 x + y 在点 p 是可用的（Available）。

主要用途：

全局公共子表达式消除：如果在点 p，表达式 x + y 是可用的，我们就可以直接使用之前计算的结果，而不用重新计算。

可用表达式分析框架

这是一个前向的 Must 分析。

D（方向）：前向。
V（值域）：表达式的集合。
M（交汇运算）：交集（ $\cap$ ）。必须在所有到达路径上都计算过该表达式，它才算「可用」。
F（传递函数）：
- $\mathrm{e}\_\operatorname{gen}_B$ ：基本块 $B$ 生成的表达式集合（在 $B$ 中计算且操作数随后未被重定义）。
- $\mathrm{e}\_\operatorname{kill}_B$ ：基本块 $B$ 杀死的表达式集合（表达式的任意一个操作数在 $B$ 中被重定义）。

方程组：

块内传递方程：
$\operatorname{OUT}[B] = \mathrm{e}\_\operatorname{gen}_B \cup (\operatorname{IN}[B] - \mathrm{e}\_\operatorname{kill}_B)$
块间汇集方程：
$\operatorname{IN}[B] = \bigcap_{P \in \operatorname{pred}(B)} \operatorname{OUT}[P]$

初始化陷阱

对于使用交集（ $\cap$ ）作为交汇运算的 Must 分析，迭代算法的初始化非常关键。

$\operatorname{OUT}[\mathrm{ENTRY}] = \empty$ （入口处没有任何表达式可用）。
对于所有其他基本块 $B$ ，必须初始化 $\operatorname{OUT}[B] = U$ （全集，即程序中所有表达式的集合）。

如果初始化为空集， $\empty \cap \text{任何集合} = \empty$ ，那么结果将永远是空集，我们无法发现任何可用的表达式。初始化为全集是为了从「最乐观」的假设开始，通过迭代逐步剔除不满足条件的表达式（求最大不动点）。

迭代求解算法

这一组方程组通过迭代算法求解。由于交汇运算是交集（Must Analysis），算法从「最大的集合」开始逐步缩小，直到达到不动点。

算法步骤：

初始化：
- $\operatorname{OUT}[\mathrm{ENTRY}] = \empty$
- 对所有其他基本块 $B$ （除 ENTRY 外）， $\operatorname{OUT}[B] = U$ （全集，即程序中所有表达式的集合）。
迭代：

$\begin{align*} &\mathbf{while}\ (\text{某个 } \operatorname{OUT} \text{ 值发生改变}): \\ &\quad \mathbf{for} \ (\text{除 ENTRY 之外的每个基本块 } B): \\ &\qquad (1) \ \operatorname{IN}[B] = \bigcap_{P \in \operatorname{pred}(B)} \operatorname{OUT}[P] \\ &\qquad (2) \ \operatorname{OUT}[B] = \mathrm{e}\_\operatorname{gen}_B \cup (\operatorname{IN}[B] - \mathrm{e}\_\operatorname{kill}_B) \\ \end{align*}$

算法的终止性与最大不动点

单调性：由于初始化为全集 $U$ ，且交集运算（ $\cap$ ）只会让集合变小或保持不变，因此在迭代过程中， $\operatorname{OUT}[B]$ 集合是单调递减的（只减不增）。
终止性：集合大小的下界是空集 $\empty$ ，因此算法必然在有限步内终止。
解的性质：该算法计算出的是满足方程组的最大不动点。这意味着它保留了尽可能多的「可用表达式」信息，是最精确且安全的解。

三种数据流分析对比总结

特性	到达定值	活跃变量	可用表达式
域	定值的集合	变量的集合	表达式的集合
方向	前向	后向	前向
性质	May（可能到达）	May（可能被用）	Must（一定可用）
交汇运算	并集（ $\cup$ ）	并集（ $\cup$ ）	交集（ $\cap$ ）
传递函数 $f_B$	$\operatorname{gen}_B \cup (x - \operatorname{kill}_B)$	$\operatorname{use}_B \cup (x - \operatorname{def}_B)$	$\mathrm{e}\_\operatorname{gen}_B \cup (x - \mathrm{e}\_\operatorname{kill}_B)$
方程组	$\begin{aligned} \operatorname{OUT}[B] & = f_B(\operatorname{IN}[B]) \\ \operatorname{IN}[B] & = \bigcup_{P \in \operatorname{pred}(B)} \operatorname{OUT}[P] \end{aligned}$	$\begin{aligned} \operatorname{IN}[B] & = f_B(\operatorname{OUT}[B]) \\ \operatorname{OUT}[B] & = \bigcup_{S \in \operatorname{succ}(B)} \operatorname{IN}[S] \end{aligned}$	$\begin{aligned} \operatorname{OUT}[B] & = f_B(\operatorname{IN}[B]) \\ \operatorname{IN}[B] & = \bigcap_{P \in \operatorname{pred}(B)} \operatorname{OUT}[P] \end{aligned}$
边界条件	$\operatorname{OUT}[\mathrm{ENTRY}] = \empty$	$\operatorname{IN}[\mathrm{EXIT}] = \empty$	$\operatorname{OUT}[\mathrm{ENTRY}] = \empty$
非边界初始值	$\operatorname{OUT}[B] = \empty$	$\operatorname{IN}[B] = \empty$	$\operatorname{OUT}[B] = U$

数据流分析的通用框架

通过对比上述三种分析，我们可以抽象出一个数据流分析的通用迭代算法框架。这个框架利用半格理论的符号来统一描述。

定义符号：

$\bigwedge$ （Meet 运算）：对应交汇运算（ $\cup$ 或 $\cap$ ）。
$\top$ $⊤$ （Top 元素）：对应格的顶端元素，也是交汇运算的「单位元」。
- 对于 $\cup$ 运算， $\top = \empty$ （空集）。
- 对于 $\cap$ 运算， $\top = U$ （全集）。
$v_{\mathrm{ENTRY}}/v_{\mathrm{EXIT}}$ ：边界条件初始值。

前向分析通用算法（Forward）：适用于到达定值分析、可用表达式分析。

$\begin{align*} & 1) \ \operatorname{OUT}[\mathrm{ENTRY}] = v_{\mathrm{ENTRY}} \\ & 2) \ \mathbf{for} \ (\text{除 ENTRY 之外的每个基本块 } B) \ \operatorname{OUT}[B] = \top \\ & 3) \ \mathbf{while} \ (\text{某个 OUT 值发生了改变}) \\ & 4) \qquad \mathbf{for} \ (\text{除 ENTRY 之外的每个基本块 } B)\ \{ \\ & 5) \qquad \qquad \operatorname{IN}[B] = \bigwedge_{P \in \operatorname{pred}(B)} \operatorname{OUT}[P] \\ & 6) \qquad \qquad \operatorname{OUT}[B] = f_B(\operatorname{IN}[B]) \\ & 7) \qquad \} \end{align*}$

后向分析通用算法（Backward）：适用于活跃变量分析。

$\begin{align*} & 1) \ \operatorname{IN}[\mathrm{EXIT}] = v_{\mathrm{EXIT}} \\ & 2) \ \mathbf{for} \ (\text{除 EXIT 之外的每个基本块 } B) \ \operatorname{IN}[B] = \top \\ & 3) \ \mathbf{while} \ (\text{某个 IN 值发生了改变}) \\ & 4) \qquad \mathbf{for} \ (\text{除 EXIT 之外的每个基本块 } B)\ \{ \\ & 5) \qquad \qquad \operatorname{OUT}[B] = \bigwedge_{S \in \operatorname{succ}(B)} \operatorname{IN}[S] \\ & 6) \qquad \qquad \operatorname{IN}[B] = f_B(\operatorname{OUT}[B]) \\ & 7) \qquad \} \end{align*}$

数据流分析的理论基础

在实施上述迭代算法时，我们需要回答以下几个核心理论问题：

算法一定会收敛吗？
- 是的。
- 单调性：传递函数 $f_B$ 和交汇运算 $\bigwedge$ 都是单调的。
- 有限高度：数据流值的集合（格）是有限的，或者具有有限的高度。
- 在迭代过程中，集合的值单调变化（对于 $\cup$ 问题单调递增，对于 $\cap$ 问题单调递减），且有界，因此必然会在有限步内达到不动点并停止。
算法的解是正确的吗？（安全性）
- 是的，是安全的近似。
- 我们追求的解必须能够包含所有可能的动态执行路径产生的结果。
- 通过将交汇运算 $\bigwedge$ 设计为保守的（如可用表达式中的 $\cap$ 要求所有路径都计算过，活跃变量中的 $\cup$ 只要有一条路径使用就算），我们保证了结果的安全性。
得到的解有多精确？
- 迭代算法计算出的是最大不动点（Maximal Fixed Point, MFP）。
- 注意：由于程序中存在不可达路径（控制流图无法区分路径是否真的会执行），MFP 可能不如交汇所有路径（Meet Over Paths, MOP）的理想解精确，但在绝大多数数据流框架（如上述三种）中，如果传递函数是可分配（Distributive）的，则 MFP = MOP。
  - 注：上述三种经典分析都是可分配的，因此迭代解就是最精确的解。

为什么初始化很重要？

正如「可用表达式」分析中指出的， $\operatorname{OUT}[B]$ 初始化为全集 $U$ （即 $\top$ ），是为了让我们从格的「最高点」开始下降。这能让我们找到最大不动点（包含最多的可用表达式信息）。如果初始化为空集，我们得到的将是最小不动点（没有表达式可用），这是安全的，但对于优化来说太保守了（没用的解）。

简单常量传播

常量传播（Constant Propagation）不仅可以作为一种优化手段，其本身也可以看作是一个数据流分析问题。

我们需要为每个变量维护一个状态，状态空间构成一个半格：

$\text{UNDEF}$ ：未定义。表示变量尚未被赋值，或者我们还不知道它的值（乐观假设）。
Constant $c$ ：确定的常量值。
$\text{NAC}$ (Not-A-Constant)：不是常量。表示变量在不同路径上被赋予了不同的值，或者被赋予了运行时才能确定的输入值。

交汇规则：

$\text{UNDEF} \land v = v$
$\text{NAC} \land v = \text{NAC}$
$c_1 \land c_2 = \begin{cases} c_1 & \text{if } c_1 = c_2 \\ \text{NAC} & \text{if } c_1 \neq c_2 \end{cases}$

循环优化基础

程序的大部分执行时间通常花在循环上（90/10 法则），因此循环是优化的重点。为了对循环进行优化（如代码外提、强度削弱），编译器首先需要在控制流图中识别出循环。

支配节点

支配（Dominance）是流图中节点间的一种控制关系，是识别循环的基石。

支配关系

如果从流图的入口节点（Entry）到达节点 $n$ 的每一条路径都必须经过节点 $d$ ，则称 $d$ 支配 $n$ ，记为 $d \operatorname{dom} n$ 。

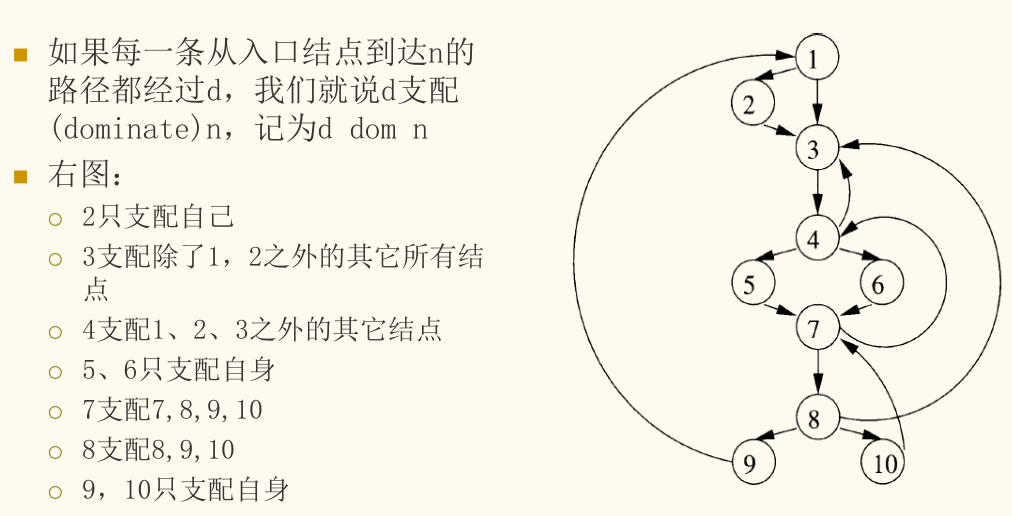
性质：

每个节点都支配它自己。
支配关系具有传递性。
直接支配节点（Immediate Dominator, idom）：严格支配 $n$ 的节点集合中，距离 $n$ 最近的那个节点（在支配树中是 $n$ 的父节点）。

支配节点树

支配节点树（Dominator Tree）：我们可以用树结构来表示支配关系。根节点是 Entry。如果 $d$ 是 $n$ 的直接支配节点，则在树中存在一条边 $d \to n$ 。

寻找支配节点本身就是一个数据流分析问题：

方向：前向。
值域：节点集合的幂集。
交汇：交集（ $\cap$ ）。（必须在所有路径上都出现才算支配）。
方程：
$\operatorname{OUT}[B] = \{B\} \cup \left( \bigcap_{P \in \operatorname{pred}(B)} \operatorname{OUT}[P] \right)$
即：支配 $B$ 的节点集合 = $B$ 自身 + ( $B$ 的所有前驱的支配节点的交集)。

迭代求解算法

求解支配节点的过程也是一个典型的前向数据流分析问题。

初始化注意事项

由于交汇运算是交集（ $\cap$ ），这是一个 Must Analysis。为了求得最大不动点（即最精确的支配关系），除 ENTRY 块外，所有基本块的初始支配集必须初始化为所有节点的集合 $N$ （即全集）。如果初始化为空集，交集运算会导致结果始终为空。

算法步骤：

初始化：
- $\operatorname{OUT}[\mathrm{ENTRY}] = \{\mathrm{ENTRY}\}$
- 对于所有其他节点 $B$ ， $\operatorname{OUT}[B] = N$ （流图中所有节点的集合）。
迭代：

$\begin{align} &\mathbf{while}\ (\text{某个 } \operatorname{OUT} \text{ 集合发生改变}): \\ &\quad \mathbf{for} \ (\text{除 ENTRY 之外的每个节点 } B): \\ &\qquad (1) \ \operatorname{IN}[B] = \bigcap_{P \in \operatorname{pred}(B)} \operatorname{OUT}[P] \\ &\qquad (2) \ \operatorname{OUT}[B] = \{B\} \cup \operatorname{IN}[B] \\ \end{align}$

深度优先生成树与边的分类

为了识别循环，我们需要分析控制流图的结构。通过深度优先搜索（DFS）遍历流图，我们可以构建一棵深度优先生成树（Depth-First Spanning Tree, DFST），并对流图中的边进行分类。

在构建 DFST 的过程中，我们可以记录每个节点的访问顺序，称为 DFN(Depth-First Number)。

通常采用逆序记录（从 $c$ 递减到 1），或者直接记录访问时间戳。

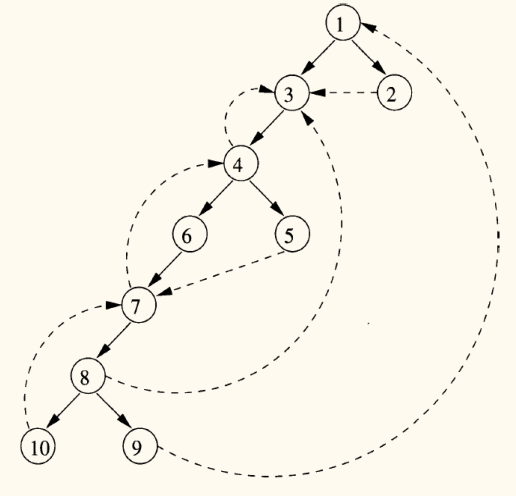
基于 DFST，流图中的边 $m \to n$ 可以分为三类：

前进边：从节点 $m$ $m$ 到其在 DFST 中的某个真后代的边（包括 DFST 树本身的边）。
- 从祖先指向后代。
后退边：从节点 $m$ $m$ 到其在 DFST 中的某个祖先的边（ $m$ $m$ 也可以指向自身）。
- 从后代指向祖先。
交叉边： $m$ $m$ 和 $n$ $n$ 既不是对方的祖先也不是后代。在 DFST 中，交叉边总是从右指向左。
- 节点间无祖先/后代关系。

回边与可归约性

回边（Back Edge）是识别循环的关键特征。

回边

如果流图中的一条边 $a \to b$ ，其头节点 $b$ 支配尾节点 $a$ （即 $b \operatorname{dom} a$ ），则称该边为回边。

直观理解：回边是指向循环头的边。

性质：

每条回边都是后退边（在 DFST 中），但并非所有后退边都是回边。
可归约流图（Reducible Flow Graph）：如果一个流图的 DFST 中，所有的后退边都是回边，则称该流图是可归约的。
- 结构化程序设计（不使用 goto乱跳）产生的流图通常都是可归约的。
- 在可归约流图中，我们关注的「循环」就是由回边定义的。

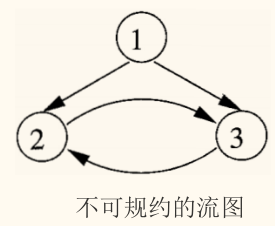
不可规约的流图删除所有回边后，仍然存在环路，循环存在多个入口。这种流图通常源自复杂的控制流（如 goto 语句），编译器对其优化能力有限。

流图的深度

流图的深度是估算迭代数据流分析复杂度的重要指标。

定义：流图中任意一条无环路径上包含的后退边的最大数量。
意义：对于大多数数据流分析（如到达定值），如果流图的深度为 $d$ ，那么迭代算法通常只需要 $d+2$ 遍扫描即可收敛。
直观上，这个深度通常不会大于程序中循环的嵌套层数。

自然循环

在编译器中，我们通常关注自然循环。自然循环必须具备两个性质：

有一个唯一的入口节点，称为循环头。循环头支配循环内的所有节点。
存在至少一条进入循环头的回边。

给定一条回边 $n \to d$ （ $d$ 是头， $n$ 是尾），自然循环是由 $d$ 加上所有能够不经过 $d$ 而到达 $n$ 的节点组成的集合。简单来说，就是回边形成环路上的所有节点。

自然循环构造算法

给定流图 $G$ 和一条回边 $n \to d$ ，我们可以通过以下算法找到该自然循环中的所有节点。

输入：流图 $G$ 和回边 $n \to d$ 。
输出：回边 $n \to d$ 的自然循环中的所有节点的集合 $\mathrm{loop}$ 。

算法步骤：

初始化：令 $\mathrm{loop} = \{n, d\}$ ，并将循环头 $d$ 标记为 $\mathrm{visited}$ （已访问），以确保搜索不会越过循环头。
逆向搜索：从节点 $n$ $n$ 开始，逆向（沿着控制流边的反方向）对数据流图进行深度优先搜索（DFS）。
- 把所有访问到的前驱节点都加入 $\mathrm{loop}$ 集合，并标记为 $\mathrm{visited}$ 。
- 在搜索过程中，如果遇到已经标记为 $\mathrm{visited}$ 的节点，则停止该路径的搜索。

算法直观理解

该算法的核心思想是：自然循环包含了 $n$ 和 $d$ ，以及所有能够不经过 $d$ 而到达 $n$ 的节点。我们从 $n$ 倒着往回找前驱，只要不碰到 $d$ （因为 $d$ 支配 $n$ ，所有进入循环的外部路径都必须经过 $d$ ），找到的所有节点必然都在循环内部。

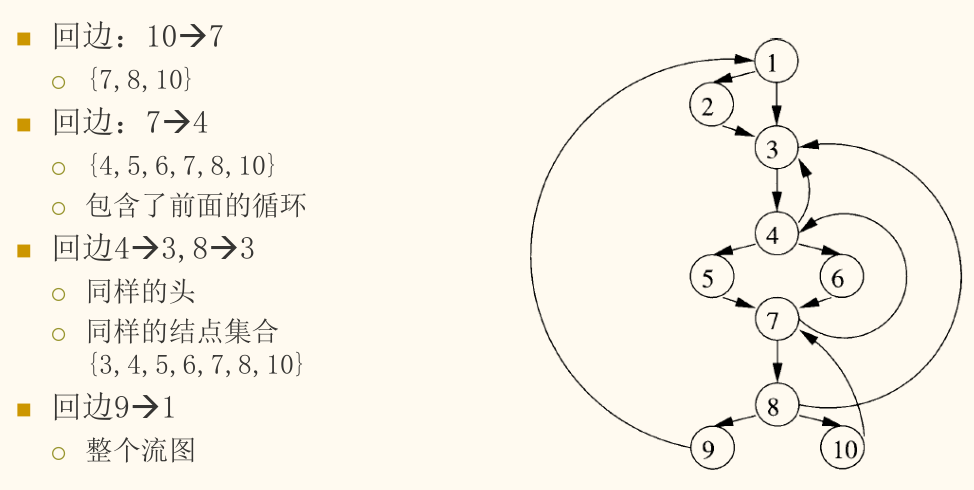
循环的嵌套：除非两个循环拥有相同的循环头，否则它们要么是分离的，要么是一个嵌套在另一个里面。最内层循环通常是优化的重点。

全局优化全景图

现代编译器的优化通常由多个 pass 组成，形成一个管道。一个典型的顺序可能是：

graph LR
    A["📊 全局常量传播"] 
    B["🔄 公共子表达式消除"]
    C["📝 复制传播"]
    D["🧹 死代码消除"]
    E["⚙️ 循环不变式外提"]
    F["💪 强度削弱"]
    G["🎯 归纳变量删除"]

    A --> B
    B --> C
    C --> D
    D --> E
    E --> F
    F --> G

    style A fill:#e1f5fe,stroke:#01579b,stroke-width:2px
    style B fill:#f3e5f5,stroke:#4a148c,stroke-width:2px
    style C fill:#e8f5e8,stroke:#1b5e20,stroke-width:2px
    style D fill:#fff3e0,stroke:#e65100,stroke-width:2px
    style E fill:#fce4ec,stroke:#880e4f,stroke-width:2px
    style F fill:#e8eaf6,stroke:#283593,stroke-width:2px
    style G fill:#e0f2f1,stroke:#004d40,stroke-width:2px

    linkStyle default stroke:#78909c,stroke-width:2px,stroke-dasharray: 5 5

这些优化往往是相互促进的。例如，常量传播可能会产生死代码；复制传播可能会暴露新的公共子表达式；循环优化可能会引入新的临时变量，需要后续的死代码消除来清理。