无穷级数

常数项级数

概念

给定数列

$$u_1, u_2, \cdots, u_n, \cdots$$

形如

$$u_1 + \cdots + u_n + \cdots$$

的和式称为 （常数项）无穷级数，简称 （常数项）级数，记作

$$\sum_{n=1}^{\infty} u_n$$

$u_n$ 称为级数的通项。

作级数前 $n$ 项和的函数 $S_n$ 称为级数的部分和，即

$$S_n = u_1 + u_2 + \cdots + u_n = \sum_{k=1}^{n} u_k$$

如果级数 $\displaystyle \sum_{n=1}^{\infty}u_n$ 部分和数列 $\{S_n\}$ 有极限 $S$，即 $\displaystyle \lim_{n \to \infty} S_n = S$，则称级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 收敛，并称 $S$ 为级数的和。

如果数列 $\{S_n\}$ 无极限，则称级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 发散。

当级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 收敛时，其部分和与和 $S$ 的差 $r_n = S - S_n$ 称为级数的余项。

$|r_n|$ 是用部分和 $S_n$ 代替级数的和 $S$ 所产生的误差。

性质

若级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 收敛，$k$ 为常数，则 $\displaystyle \sum_{n=1}^{\infty} ku_n$ 也收敛，且

$$\sum_{n=1}^{\infty} ku_n = k \sum_{n=1}^{\infty} u_n$$

若级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 和 $\displaystyle \sum_{n=1}^{\infty} v_n$ 都收敛，则 $\displaystyle \sum_{n=1}^{\infty} (u_n \pm v_n)$ 也收敛，且

$$\sum_{n=1}^{\infty} (u_n \pm v_n) = \sum_{n=1}^{\infty} u_n \pm \sum_{n=1}^{\infty} v_n$$

若级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 收敛，则对这级数的项任意加括号所成的级数

$$(u_1 + \cdots + u_{1_i}) + \cdots + (u_{i_{n-1}+1} + \cdots + u_{i_n}) + \cdots$$

仍收敛，且和不变。

---

加括号后收敛，未必收敛。如

$$\begin{aligned} (1 - 1) + (1 - 1) + \cdots = 0\\ 1 - (1 - 1) - (1 - 1) - \cdots = 1 \end{aligned}$$

级数收敛的必要条件

级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 收敛的必要条件是 $\displaystyle \lim_{n \to \infty} u_n = 0$。

级数中去掉、加上或改变有限项，级数的敛散性不变。

柯西收敛原理

级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 收敛的充分必要条件是：对任意 $\varepsilon > 0$，存在 $N \in \N$，使得 $n > m > N$ 时，有

$$|u_{m+1} + \cdots + u_n| < \varepsilon$$

即级数的部分和 $S_n$ 与 $S_m$ 之差 $|S_n - S_m| < \varepsilon$。

正项级数

正项级数

如果级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 的每一项 $u_n \ge 0$，则称 $\displaystyle \sum_{n=1}^{\infty} u_n$ 为正项级数。

正项级数 $\displaystyle \sum_{n=1}^{\infty}u_n$ 收敛的充分必要条件是：它的部分和数列 $\{S_n\}$ 有上界。

比较判别法：若两个正项级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 和 $\displaystyle \sum_{n=1}^{\infty} v_n$ 对任意 $n$ 都有 $u_n \le v_n$，则

1. 若 $\displaystyle \sum_{n=1}^{\infty} v_n$ 收敛时，则 $\displaystyle \sum_{n=1}^{\infty} u_n$ 也收敛；
2. 若 $\displaystyle \sum_{n=1}^{\infty} u_n$ 发散时，则 $\displaystyle \sum_{n=1}^{\infty} v_n$ 也发散。

若存在正整数 $N$ 及常数 $C > 0$ 使得

$$0 \le u_n \le C v_n, \quad (n > N)$$

成立，则

1. 若 $\displaystyle \sum_{n=1}^{\infty} v_n$ 收敛，则 $\displaystyle \sum_{n=1}^{\infty} u_n$ 也收敛；
2. 若 $\displaystyle \sum_{n=1}^{\infty} u_n$ 发散，则 $\displaystyle \sum_{n=1}^{\infty} v_n$ 也发散。

p-级数

讨论 $p$-级数

$$\sum_{n=1}^{\infty} \frac{1}{n^p} = 1 + \frac{1}{2^p} + \cdots$$

的敛散性。其中 $p$ 为常数。

---

$p \le 1$ 时，$\dfrac{1}{n^p} \ge \dfrac{1}{n}$，而调和级数 $\displaystyle \sum_{n=1}^{\infty} \dfrac{1}{n}$ 发散，比较判别法知 $p \le 1$ 时 $p$-级数发散。

当 $p > 1$ 时，有

$$\int_n^{n+1} \dfrac{1}{x^p} \d x \le \dfrac{1}{n^p} \le \int_{n-1}^n \dfrac{1}{x^p} \d x$$

从而 $p$-级数的部分和有

$$\begin{aligned} 1 + \int_2^{n+1} \dfrac{1}{x^p} \d x \le 1 + \sum_{i=2}^{n}\dfrac{1}{n^p} &\le 1 + \int_1^n \dfrac{1}{x^p} \d x\\ &= 1 + \dfrac{1}{1-p} x^{1-p} \as_1^{n}\\ &= 1 + \dfrac{1}{p-1} \left( 1 - n^{1-p} \right)\\ &< 1 + \dfrac{1}{p-1} \end{aligned}$$

因此 $p$-级数部分和有上界，故 $p$-级数收敛。

比较判别法的极限形式

设级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 和 $\displaystyle \sum_{n=1}^{\infty} v_n$ 都是正项级数，且 $\lim\limits_{n \to \infty} \dfrac{u_n}{v_n} = l$，则

1. 若 $0 \le l < +\infty$，且级数 $\displaystyle \sum_{n=1}^{\infty} v_n$ 收敛，则 $\displaystyle \sum_{n=1}^{\infty} u_n$ 也收敛；
2. 若 $0 < l \le +\infty$^[1]，且级数 $\displaystyle \sum_{n=1}^{\infty} v_n$ 发散，则 $\displaystyle \sum_{n=1}^{\infty} u_n$ 也发散。

比较判别法的推论

对正项级数 $\displaystyle\sum_{n=1}^{\infty} u_n$ 和 $\displaystyle\sum_{n=1}^{\infty} v_n$，若有 $\dfrac{u_{n+1}}{u_n} \le \dfrac{v_{n+1}}{v_n}$，则

1. 若 $\displaystyle\sum_{n=1}^{\infty} v_n$ 收敛，则 $\displaystyle\sum_{n=1}^{\infty} u_n$ 收敛
2. 若 $\displaystyle\sum_{n=1}^{\infty} u_n$ 发散，则 $\displaystyle\sum_{n=1}^{\infty} v_n$ 发散

证明

由题意有 $\dfrac{u_{n+1}}{v_{n+1}} \le \dfrac{u_n}{v_n}$，设

$$\lim_{n \to \infty} \dfrac{u_{n}}{v_{n}} = \rho$$

则 $\dfrac{u_n}{v_n} \ge \rho$，即 $u_n \ge \rho v_n$，从而由比较判别法知结论成立。

达朗贝尔判别法（比值判别法）

设级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 是正项级数，且 $\lim\limits_{n \to \infty} \dfrac{u_{n+1}}{u_n} = \rho$，则

1. 若 $\rho < 1$，则 $\displaystyle \sum_{n=1}^{\infty} u_n$ 收敛；
2. 若 $\rho > 1$，则 $\displaystyle \sum_{n=1}^{\infty} u_n$ 发散；
3. 若 $\rho = 1$，则级数可能收敛，可能发散。

---

达朗贝尔判别法证明

仅证明 $\rho < 1$ 时级数收敛。

由 $\displaystyle \lim_{n \to \infty} \dfrac{u_{n+1}}{u_n} = \rho < 1$，存在 $N$ 与 $\xi$，使得任意 $n > N$ 时有 $\dfrac{u_{n+1}}{u_n} < \xi < 1$。

则 $u_{n+1} < \xi u_n < \cdots < \xi^{n-N} u_{N+1}$。

而

$$\begin{aligned} \xi^{n-N} u_{N+1} &= \overbrace{\left(\dfrac{u_{N+1}}{\xi^{N+1}}\right)}^{\text{与 } n \text{ 无关，为常数}} \xi^{n+1}\\ &= C \xi^{n+1} \end{aligned}$$

即

$$u_{n+1} < C \xi^{n+1}$$

进而 $\displaystyle \sum_{n=1}^{\infty} u_n = \sum_{n=1}^{N}u_n + \sum_{n=N+1}^{\infty}u_n$ 收敛。

柯西判别法（根值判别法）

设级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 是正项级数，且 $\lim\limits_{n \to \infty} \sqrt[n]{u_n} = \rho$，则

1. 若 $\rho < 1$，则 $\displaystyle \sum_{n=1}^{\infty} u_n$ 收敛；
2. 若 $\rho > 1$，则 $\displaystyle \sum_{n=1}^{\infty} u_n$ 发散；
3. 若 $\rho = 1$，则级数可能收敛，可能发散。

---

柯西判别法证明

仅证明 $\rho < 1$ 时级数收敛。

由 $\displaystyle \lim_{n \to \infty} \sqrt[n]{u_n} = \rho < 1$，存在 $N$ 与 $\xi$，使得任意 $n > N$ 时有 $\sqrt[n]{u_n} < \xi < 1$。

则 $u_n < \xi^n$。

进而 $\displaystyle \sum_{n=1}^{\infty} u_n$ 收敛。

柯西积分判别法

设级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 是正项级数，若存在一个连续的单调减少的正值函数 $f(x)$，使得

$$u_n = f(n), \quad n = 1, 2, \cdots$$

则 $\displaystyle \sum_{n=1}^{\infty} u_n$ 与 $\displaystyle \int_1^{+\infty} f(x) \d x$ 具有相同的敛散性。

---

柯西积分判别法证明

$$\begin{aligned} u_{k-1} &= \int^{k}_{k-1} u_{k-1} \d x\\ &\ge \int^{k}_{k-1} f(x) \d x\\ &\ge \int^{k}_{k-1} u_k \d x\\ &= u_k \end{aligned}$$

则

$$\begin{aligned} \sum_{k=2}^{n}u_{k-1} &\ge \sum_{k=2}^{n}\int_{k-1}^{k}f(x) \d x = \int_{1}^{n}f(x) \d x\\ &\ge \sum_{k=2}^{n}u_k \end{aligned}$$

从而 $\displaystyle \sum_{n=1}^{\infty} u_n$ 与 $\displaystyle \int_1^{+\infty} f(x) \d x$ 具有相同的敛散性。

拉阿贝（拉比，Raabe）判别法

对正项级数 $\displaystyle\sum_{n=1}^{\infty} u_n$，且 $\lim\limits_{n \to \infty} n\left(\dfrac{u_n}{u_{n+1}} - 1\right) = p$，则

1. 若 $p > 1$，则 $\displaystyle\sum_{n=1}^{\infty} u_n$ 收敛；
2. 若 $p < 1$，则 $\displaystyle\sum_{n=1}^{\infty} u_n$ 发散。
3. 若 $p = 1$，则级数可能收敛，可能发散。

证明

仅证明 $p > 1$ 时级数收敛。则存在 $1 < r < p$，使得

$$\begin{aligned} \lim_{n\to \infty }n \left( \left(1 + \dfrac{1}{n}\right)^r - 1 \right) &= \lim\limits_{t \to 0^{+}} \dfrac{(1 + t)^r - 1}{t}\\ &= \lim\limits_{t \to 0^{+}} \dfrac{r(1 + t)^{r-1}}{1}\\ &= r \end{aligned}$$

从而有

$$\lim\limits_{n \to \infty} n\left(\dfrac{u_n}{u_{n+1}} - 1\right) = p > r = \lim\limits_{n\to \infty }n \left( \left(1 + \dfrac{1}{n}\right)^r - 1 \right)$$

因此当 $n$ 充分大时，有 $\dfrac{u_n}{u_{n+1}} > \dfrac{(n+1)^{r}}{n^r}$，即 $\dfrac{u_{n+1}}{u_n} < \dfrac{\frac{1}{(n+1)^r}}{\frac{1}{n^r}}$，因为 $r > 1$，比较判别法知 $\displaystyle\sum_{n=1}^{\infty} u_n$ 收敛。

判断正项级数

$$\sum_{n=1}^{\infty} \dfrac{n! \e^n}{n^{n+p}}$$

的敛散性。

---

解答

$$\begin{aligned} \dfrac{a_n}{a_{n+1}} &= \dfrac{n! \e^{n+1}}{n^{n+p}}\cdot \dfrac{(n+1)^{n+p+1}}{(n+1)! \e^{n+1}}\\ &= \dfrac{\left(1+\frac{1}{n}\right)^{n+p}}{\e}\\ &= \exp \left( (n+p)\ln \left(1 + \dfrac{1}{n}\right) - 1 \right) \end{aligned}$$

则

$$\begin{aligned} n\left( \dfrac{a_n}{a_{n+1}} - 1 \right) &= n\left[ \exp \left( (n+p)\ln \left(1 + \dfrac{1}{n}\right) - 1 \right) - 1 \right]\\ &\to n\left[ \exp \left((n + p)\left( \dfrac{1}{n} - \dfrac{1}{2n^2} + \dfrac{1}{3n^3} + O\left(\dfrac{1}{n^3}\right)\right) - 1 \right) - 1 \right]\\ &\to n\left[ \exp \left(\dfrac{p - \frac{1}{2}}{n} + \dfrac{\frac{1}{3}-\frac{p}{2}}{n^2} + O\left(\dfrac{1}{n^2}\right)\right) - 1 \right]\\ &\to p - \dfrac{1}{2} + \dfrac{\frac{1}{3}-\frac{p}{2}}{n} + O\left(\dfrac{1}{n}\right)\\ &\to p - \dfrac{1}{2} \end{aligned}$$

拉阿贝判别法知 $p > \dfrac{3}{2}$ 时收敛，$p < \dfrac{3}{2}$ 时发散。

---

斯特林（Stirling）公式为

$$n! \sim \sqrt{2\pi n}\left(\dfrac{n}{\e}\right)^n$$

即

$$\lim_{n \to \infty} \dfrac{n! \e^n}{n^{n+\frac{1}{2} }} = \sqrt{2 \pi}$$

实际上为

$$n! = \sqrt{2 \pi n}\left(\frac{n}{\e}\right)^{n}\left(1+\frac{1}{12 n}+\frac{1}{288 n^{2}}-\frac{139}{51840 n^{3}}-\frac{571}{2488320 n^{4}}+\cdots\right)$$

的截断形式。

任意项级数

交错级数

正负相间的级数，即形如

$$\sum_{n=1}^{\infty}(-1)^{n+1}u_n$$

的级数，其中 $u_n > 0$，称为交错级数。

莱布尼茨定理

若交错级数 $\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1} u_n$（$u_n > 0$）满足

1. $u_{n+1} \le u_n$；
2. $\lim\limits_{n \to \infty} u_n = 0$。

则交错级数 $\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1} u_n$ 收敛。余项 $r_n$ 符号与余项第一项 $(-1)^{n+2}u_{n+1}$ 符号相同，且 $|r_n| \le u_{n+1}$。

---

莱布尼茨定理证明

考察偶数项部分和 $\left\lbrace S_{2m} \right\rbrace$ 与奇数项部分和 $\left\lbrace S_{2m+1} \right\rbrace$。即

$$\begin{aligned} S_{2m} &= (u_1 - u_2) + \cdots + (u_{2m-1} - u_{2m})\\ S_{2m+1} &= (u_1 - u_2) + \cdots + (u_{2m-1} - u_{2m}) + u_{2m+1} \end{aligned}$$

由 1. 知 $\left\lbrace S_{2m} \right\rbrace$ 单调递增，而

$$0 \le S_{2m} = u_1 - (u_2 - u_3) - \cdots - (u_{2m-1} - u_{2m}) \le u_1$$

由单调有界定理知 $\left\lbrace S_{2m} \right\rbrace$ 收敛，故 $\left\lbrace S_{2m} \right\rbrace$ 极限存在，设

$$\lim_{m \to \infty} S_{2m} = S$$

而

$$S_{2m+1} = S_{2m} + u_{2m+1}$$

由 2. 知 $\lim\limits_{m \to \infty} u_{2m+1} = 0$，故

$$\begin{aligned} \lim_{m \to \infty} S_{2m+1} &= \lim_{m \to \infty} S_{2m} + \lim_{m \to \infty} u_{2m+1}\\ &= S \end{aligned}$$

因此

$$\lim_{n \to \infty} S_{2m} = \lim_{n \to \infty} S_{2m+1} = S$$

则 $\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1} u_n$ 收敛，且 $0\le S \le u_1$。

余项 $r_n$ 可写作

$$r_n = (-1)^{n+2}(u_{n+1} - u_{n+2} + \cdots)$$

则

$$|r_n| = u_{n+1} - u_{n+2} + \cdots$$

也为交错级数，从而 $|r_n| \le u_{n+1}$。

绝对收敛与条件收敛

若级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 的各项绝对值级数 $\displaystyle \sum_{n=1}^{\infty} |u_n|$ 收敛，则称 $\displaystyle \sum_{n=1}^{\infty} u_n$ 绝对收敛。

若级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 收敛，而 $\displaystyle \sum_{n=1}^{\infty} |u_n|$ 发散，则称 $\displaystyle \sum_{n=1}^{\infty} u_n$ 条件收敛。

绝对收敛级数必定收敛。

证明

设 $\displaystyle \sum_{n=1}^{\infty} u_n$ 绝对收敛，即 $\displaystyle \sum_{n=1}^{\infty} |u_n|$ 收敛。

令

$$v_n = \dfrac{1}{2}(|u_n| + u_n)$$

则 $0 \le v_n \le |u_n|$，比较判别法有 $\displaystyle \sum_{n=1}^{\infty} v_n$ 收敛。从而 $\displaystyle \sum_{n=1}^{\infty} 2 v_n$ 收敛。

而 $u_n = 2v_n - |u_n|$，收敛级数的基本性质有

$$\sum_{n=1}^{\infty} u_n = \sum_{n=1}^{\infty} 2v_n - \sum_{n=1}^{\infty} |u_n|$$

从而 $\displaystyle \sum_{n=1}^{\infty} u_n$ 收敛。

类似地令

$$w_n = \dfrac{1}{2}(|u_n| - u_n)$$

• 若级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 绝对收敛，则 $\displaystyle \sum_{n=1}^{\infty}v_n$ 与 $\displaystyle \sum_{n=1}^{\infty}w_n$ 均收敛，且 $\displaystyle \sum_{n=1}^{\infty}u_n = \sum_{n=1}^{\infty}v_n - \sum_{n=1}^{\infty}w_n$。
• 若级数 $\displaystyle \sum_{n=1}^{\infty} u_n$ 条件收敛，则 $\displaystyle \sum_{n=1}^{\infty}v_n$ 与 $\displaystyle \sum_{n=1}^{\infty}w_n$ 均发散。

因此绝对值级数 $\displaystyle \sum_{n=1}^{\infty}|u_n|$ 发散不能断定级数 $\displaystyle \sum_{n=1}^{\infty}u_n$ 发散。

但若应用达朗贝尔判别法和柯西判别法时，绝对值级数发散，则原级数必发散。

绝对收敛级数 $\displaystyle\sum_{n=1}^{\infty} u_n$ 的更序级数（即将级数项重新排列）$\displaystyle\sum_{n=1}^{\infty} u'_n$ 仍为绝对收敛级数，且 $\displaystyle\sum_{n=1}^{\infty} u'_n = \displaystyle\sum_{n=1}^{\infty} u_n$。

证明

先证明 $\displaystyle\sum_{n=1}^{\infty} u_n$ 为收敛的正项级数。

考虑更序级数 $\displaystyle\sum_{n=1}^{\infty} u'_n$ 部分和 $S_k'$，因为

$$u_1' = u_{n_1},\, \cdots,\, u_k' = u_{n_k}$$

取 $n \ge \max \left\lbrace n_1, \cdots, n_{k} \right\rbrace$，则有

$$\begin{aligned} S_{k}' &= u_1' + \cdots + u_k'\\ &= u_{n_1} + \cdots + u_{n_k}\\ &\le u_1 + \cdots + u_n\\ &= S_n \end{aligned}$$

对于正项级数 $\displaystyle\sum_{n=1}^{\infty} u_n$ 的和 $S$，有 $S_n \le S$，于是对一切 $k$ 有 $S_k' \le S$，从而 $\displaystyle\sum_{n=1}^{\infty} u'_n$ 收敛。

设其和为 $S'$，则 $S' \le S$。

而 $\displaystyle\sum_{n=1}^{\infty} u_n$ 也可以看作是 $\displaystyle\sum_{n=1}^{\infty} u'_n$ 的更序级数，故 $S \le S'$。从而 $S = S'$。

再证明 $\displaystyle\sum_{n=1}^{\infty} u_n$ 为任意绝对收敛级数的情形。

令

$$\left\lbrace\begin{aligned} v_n &= \dfrac{1}{2} (|u_n| + u_n)\\ w_n &= \dfrac{1}{2} (|u_n| - u_n) \end{aligned}\right.$$

显然有 $0 \le v_n, w_n \le |u_n|$。

因为 $\displaystyle\sum_{n=1}^{\infty} |u_n|$ 收敛，则级数 $\displaystyle\sum_{n=1}^{\infty} v_n$ 和级数 $\displaystyle\sum_{n=1}^{\infty} w_n$ 收敛。不妨设 $\displaystyle\sum_{n=1}^{\infty} v_n = V, \displaystyle\sum_{n=1}^{\infty} w_n = W$。

因为 $u_n = v_n - w_n, |u_n| = v_n + w_n$，则

$$\displaystyle\sum_{n=1}^{\infty} u_n = V - W,\quad \displaystyle\sum_{n=1}^{\infty} |u_n| = V + W$$

由上面证明过的情形有，$\displaystyle\sum_{n=1}^{\infty} |u_n|$ 的更序级数 $\displaystyle\sum_{n=1}^{\infty} |u'_n|$ 成立

$$\displaystyle\sum_{n=1}^{\infty} |u'_n| = V + W$$

即更序级数 $\displaystyle\sum_{n=1}^{\infty} u'_n$ 绝对收敛。

再设 $\displaystyle\sum_{n=1}^{\infty} v'_n$ 和 $\displaystyle\sum_{n=1}^{\infty} w'_n$ 分别为 $\displaystyle\sum_{n=1}^{\infty} v_n$ 和 $\displaystyle\sum_{n=1}^{\infty} w_n$ 的更序级数，则同理有

$$\displaystyle\sum_{n=1}^{\infty} v'_n = V,\quad \displaystyle\sum_{n=1}^{\infty} w'_n = W$$

而 $u_n' = v_n' - w_n'$，所以

$$\begin{aligned} \displaystyle\sum_{n=1}^{\infty} u'_n &= \displaystyle\sum_{n=1}^{\infty} (v'_n-w'_n)\\ &= V - W\\ &= \displaystyle\sum_{n=1}^{\infty} u_n \end{aligned}$$

得证。

黎曼重排定理

对于条件收敛级数 $\displaystyle\sum_{n=1}^{\infty} u_n$，可以重新排列其顺序，使得新的级数 $\displaystyle\sum_{n=1}^{\infty} u'_n$ 收敛到任意给定的值，或者发散。

阿贝尔（Abel）变换

记 $B_n = \displaystyle \sum_{k=1}^{n}b_k$，则

$$\begin{aligned} \sum_{k=n}^{m}a_{k}b_{k} &= \sum_{k=n}^{m}a_{k}(B_{k} - B_{k-1})\\ &= \sum_{k=n}^{m}a_{k}B_{k} - \sum_{k=n}^{m}a_{k}B_{k-1}\\ &= \sum_{k=n}^{m}a_{k}B_{k} - \sum_{k=n-1}^{m-1}a_{k+1}B_{k}\\ &= \sum_{k=n}^{m}(a_{k}-a_{k+1})B_{k} + a_{m+1}B_{m} - a_{n}B_{n-1} \end{aligned}$$

---

记前向差分算子 $\Delta$ 为 $\Delta a_{n} = a_{n+1} - a_{n}$，则有阿贝尔变换

$$\begin{aligned} \sum_{k=n}^{m}a_{k}\Delta b_{k} = a_{m+1}b_{m+1} - a_n b_n - \sum_{k=n}^{m} b_{k+1} \Delta a_{k} \end{aligned}$$

阿贝尔判别法

若

1. 级数 $\displaystyle\sum_{n=1}^{\infty} b_n$ 收敛
2. 数列 $\left\lbrace a_n \right\rbrace$ 单调有界

则级数 $\displaystyle\sum_{n=1}^{\infty} a_n b_n$ 收敛。

证明

级数 $\displaystyle\sum_{n=1}^{\infty} b_n$ 收敛得，存在 $M$ 使得 $|B_n| \le M$。同时 $\left\lbrace a_n \right\rbrace$ 单调得，$a_{k} - a_{k+1}$ 同号。

$$\begin{aligned} \left\lvert \sum_{k=n}^{m}a_{k}b_{k} \right\rvert &= \left\lvert \sum_{k=n}^{m}(a_{k}-a_{k+1})B_{k} + a_{m+1}B_{m} - a_{n}B_{n-1} \right\rvert\\ &\le \sum_{k=n}^{m}\left\lvert a_{k}-a_{k+1} \right\rvert \left\lvert B_{k} \right\rvert + \left\lvert a_{m+1}B_{m} \right\rvert + \left\lvert a_{n}B_{n-1} \right\rvert\\ &\le M \left(\sum_{k=n}^{m}\left\lvert a_{k}-a_{k+1} \right\rvert + \left\lvert a_{m+1} \right\rvert + \left\lvert a_n \right\rvert\right)\\ &= M\left(\left\lvert a_{n} - a_{m+1} \right\rvert + \left\lvert a_{m+1} \right\rvert + \left\lvert a_n \right\rvert\right) \end{aligned}$$

又 $\left\lbrace a_n\right\rbrace$ 有界，故 $\displaystyle\sum_{n=1}^{\infty} a_nb_n$ 任意部分和有界，从而 $\displaystyle\sum_{n=1}^{\infty} a_n b_n$ 收敛。

狄利克雷判别法

若

1. 级数 $\displaystyle\sum_{n=1}^{\infty} b_n$ 部分和数列有界
2. 数列 $\left\lbrace a_n \right\rbrace$ 单调趋于零

则级数 $\displaystyle\sum_{n=1}^{\infty} a_n b_n$ 收敛。

柯西乘积

若级数 $\displaystyle\sum_{n=1}^{\infty} a_n$ 和 $\displaystyle\sum_{n=1}^{\infty} b_n$ 收敛，则称 $\displaystyle\sum_{n=1}^{\infty} c_n$ 为级数 $\displaystyle\sum_{n=1}^{\infty} a_n$ 和 $\displaystyle\sum_{n=1}^{\infty} b_n$ 的柯西乘积，其中

$$\begin{aligned} c_n = \sum_{k=1}^{n}a_{k}b_{n-k+1} \end{aligned}$$

即按对角线求和。

柯西定理

若级数 $\displaystyle\sum_{n=1}^{\infty} u_n$ 和 $\displaystyle\sum_{n=1}^{\infty} v_n$ 绝对收敛，和分别为 $s, \sigma$，则它们各项之积 $u_iv_j$ 按任何方式排列所构成的级数绝对收敛，且和为 $s\sigma$。

证明

用 $w_1, \cdots, w_n, \cdots$ 表示按某一种次序排列 $u_i v_j$ 所构成的一个数列，考虑级数

$$|w_1| + \cdots |w_n| + \cdots$$

设 $s_n^{*}$ 是它的部分和

$$s_n^{*} = \sum_{k=1}^{n}|w_k| = \sum_{k=1}^{n} |u_{n_k}v_{m_k}|$$

记

$$\mu = \max \left\lbrace n_1, \cdots, n_n, m_1, \cdots, m_n \right\rbrace$$

又记

$$U_{\mu}^{*} = \sum_{k=1}^{\mu}|u_{k}|\\ V_{\mu}^{*} = \sum_{k=1}^{\mu}|v_{k}|$$

由 $\displaystyle\sum_{n=1}^{\infty} u_n$ 和 $\displaystyle\sum_{n=1}^{\infty} v_n$ 绝对收敛，设 $U^{*} = \displaystyle\sum_{n=1}^{\infty} |u_n|, V^{*} = \displaystyle\sum_{n=1}^{\infty} |v_n|$，则有 $U_{\mu}^{*} \le U^{*}, V_{\mu}^{*} \le V^{*}_{\mu}$，从而有

$$\begin{aligned} s_n^{*} &= \sum_{k=1}^{n} |u_{n_k}v_{m_k}|\\ &\le \sum_{k=1}^{n} |u_{n_k}||v_{m_k}|\\ &\le \sum_{k=1}^{n} |u_{n_k}| \sum_{k=1}^{n} |v_{m_k}|\\ &\le \sum_{k=1}^{\mu} |u_{k}| \sum_{k=1}^{\mu} |v_{k}|\\ &\le U_{\mu}^{*}V_{\mu}^{*}\\ &\le U^{*}V^{*} \end{aligned}$$

由整项级数收敛基本定理，$\displaystyle\sum_{n=1}^{\infty} |w_n|$ 收敛，即 $\displaystyle\sum_{n=1}^{\infty} w_n$ 绝对收敛，因此其更序级数绝对收敛。

为方便计算，按正方形法排列所构成的级数进行求和，即

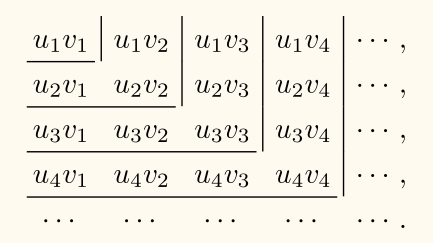
$$\begin{aligned} \displaystyle\sum_{n=1}^{\infty} w'_n &= u_1 v_1 + (u_1 v_2 + u_2 v_2 + u_2 v_1) + \cdots \end{aligned}$$

设 $\displaystyle\sum_{n=1}^{\infty} w'_n$ 部分和为 $W_n$，则 $W_n = s_n \sigma_n$，于是

$$\begin{aligned} \displaystyle\sum_{n=1}^{\infty} w'_n &= \lim\limits_{n \to \infty} W_n\\ &= \lim\limits_{n \to \infty} s_n \sigma_n\\ &= s\sigma \end{aligned}$$

从而得证。

函数项级数

给定定义在区间 $I$ 的函数列

$$u_1(x), \cdots, u_n(x), \cdots$$

则形式和

$$\displaystyle\sum_{n=1}^{\infty} u_n(x)$$

称为定义在区间 $I$ 上的函数项级数。

对每一个确定的值 $x_0 \in I$，函数项级数成为常数项级数，若常数项级数

$$\displaystyle\sum_{n=1}^{\infty} u_n(x_0)$$

收敛，则称函数项级数在 $x_0$ 处收敛，点 $x_0$ 称为函数项级数的收敛点。否则称函数项级数在 $x_0$ 处发散，点 $x_0$ 称为函数项级数的发散点。

收敛点的全体称为函数项级数的收敛域，发散点的全体称为函数项级数的发散域。

对于收敛域内任一点 $x$，函数项级数成为一收敛的常数项级数，故可定义函数项级数的和函数 $S(x)$，即

$$S(x) = \displaystyle\sum_{n=1}^{\infty} u_n(x)$$

及函数项级数前 $n$ 项的部分和为 $S_n(x)$，收敛域上有

$$\lim\limits_{n \to \infty}S_n(x) = S(x)$$

此时称

$$r_n(x) = S(x) - S_n(x) = \displaystyle\sum_{k=n+1}^{\infty} u_k(x)$$

为函数项级数的余项。并有 $\lim\limits_{n \to \infty} r_n(x) = 0$。

对函数项级数 $S(x) = \displaystyle\sum_{n=1}^{\infty} u_n(x)$，且任意 $u_n(x)$ 连续，不一定有下面的结论成立：

• $S(x)$ 连续（如 $u_n(x) = x^n - x^{n-1}$ 在 $(-1, 1]$ 上不成立）
• $S'(x) = \displaystyle\sum_{n=1}^{\infty} u'_n(x)$
• $\displaystyle \int S(x) \d x = \sum_{n=1}^{\infty} \int u_n(x) \d x$

上面的问题在于两个及以上极限过程的顺序问题，即两个极限何时可以交换。

一致收敛

设函数项级数

$$u_{1}(x)+\cdots+u_{n}(x)+\cdots$$

在区间 $I$ 上收敛于和函数 $S(x)$。

即对于区间 $I$ 上的每一个值 $x_{0}$，数项级数 $\displaystyle \sum_{n=1}^{\infty} u_{n}\left(x_{0}\right)$ 收敛于 $S\left(x_{0}\right)$，即部分和数列 $S_{n}\left(x_{0}\right)=\displaystyle \sum_{i=1}^{n} u_{i}\left(x_{0}\right)$ 收敛于 $S\left(x_{0}\right)(n \to \infty)$。

则对于任意给定的 $\varepsilon>0$ 以及区间 $I$ 上的每一个固定点 $x_{0}$，都存在一个正整数 $N$，使得当 $n>N$ 时，有

$$\left|S\left(x_{0}\right)-S_{n}\left(x_{0}\right)\right|<\varepsilon$$

即

$$\left|r_{n}\left(x_{0}\right)\right|=\left|\sum_{i=n+1}^{\infty} u_{i}\left(x_{0}\right)\right|<\varepsilon$$

这里的 $N$ 一般不仅依赖于 $\varepsilon$，而且还依赖于 $x_{0}$，记为 $N(x_0, \varepsilon)$。这种收敛即为逐点收敛。

若对某一函数项级数，都能有一个这样的正整数 $N$，使得其仅依赖于 $\varepsilon$ 而不依赖于 $x_0$，即对于 $I$ 上任意一点 $x_0$ 都有 $N = N(\varepsilon)$，则称该函数项级数在区间 $I$ 上一致收敛。

柯西一致收敛准则

设函数项级数 $\displaystyle\sum_{n=1}^{\infty} u_n(x)$，若对任意给定的 $\varepsilon > 0$，都存在一个正整数 $N$，使得当 $n > N$ 时，对于区间 $I$ 上的任意一点 $x$ 都有

$$\left|r_n(x)\right| = \left|S(x) - S_n(x)\right| < \varepsilon$$

则称函数项级数 $\displaystyle\sum_{n=1}^{\infty} u_n(x)$ 在区间 $I$ 上一致收敛于 $S(n)$，也称 $\left\lbrace S_n(x) \right\rbrace$ 在区间 $I$ 上一致收敛于 $S(x)$。记作 $\displaystyle\sum_{n=1}^{\infty} u_n(x) \rightrightarrows S(x)$。

---

几何意义：$n > N(\varepsilon)$ 时，区间 $I$ 上所有曲线 $y = S_n(x)$ 都将位于曲线

$$y_1 = S(x) + \varepsilon\\ y_2 = S(x) - \varepsilon$$

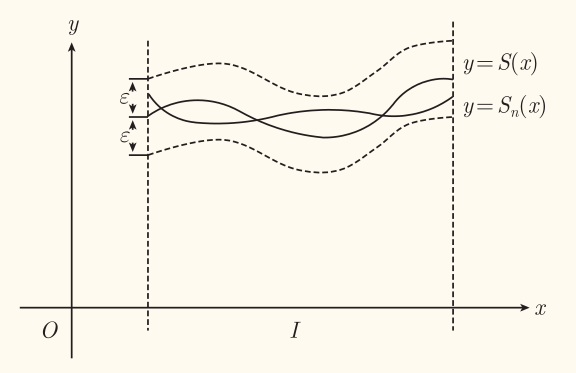
GGB 重出江湖。

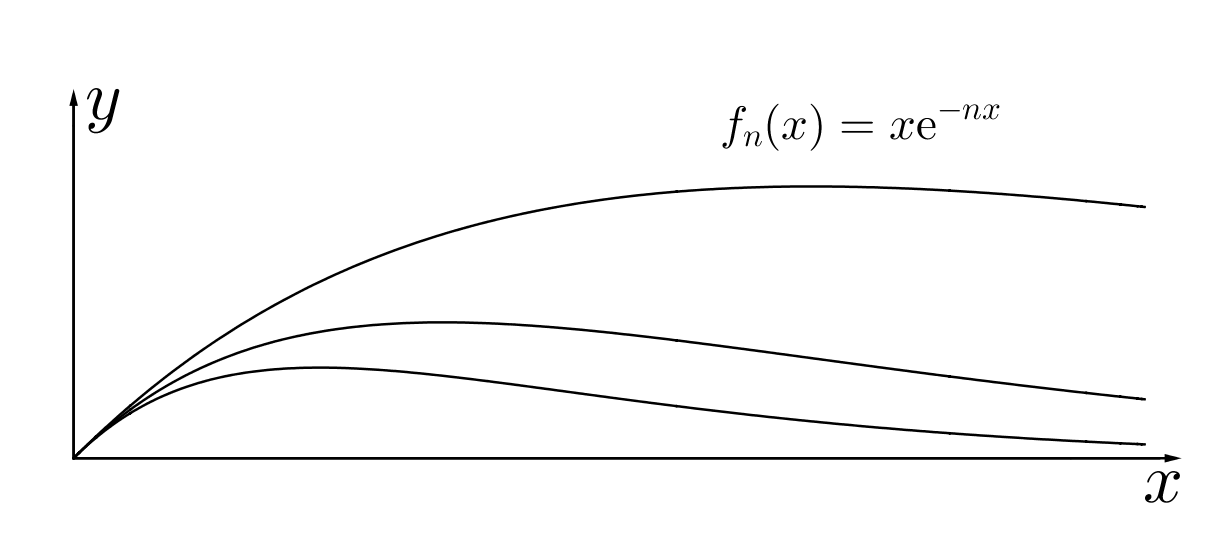
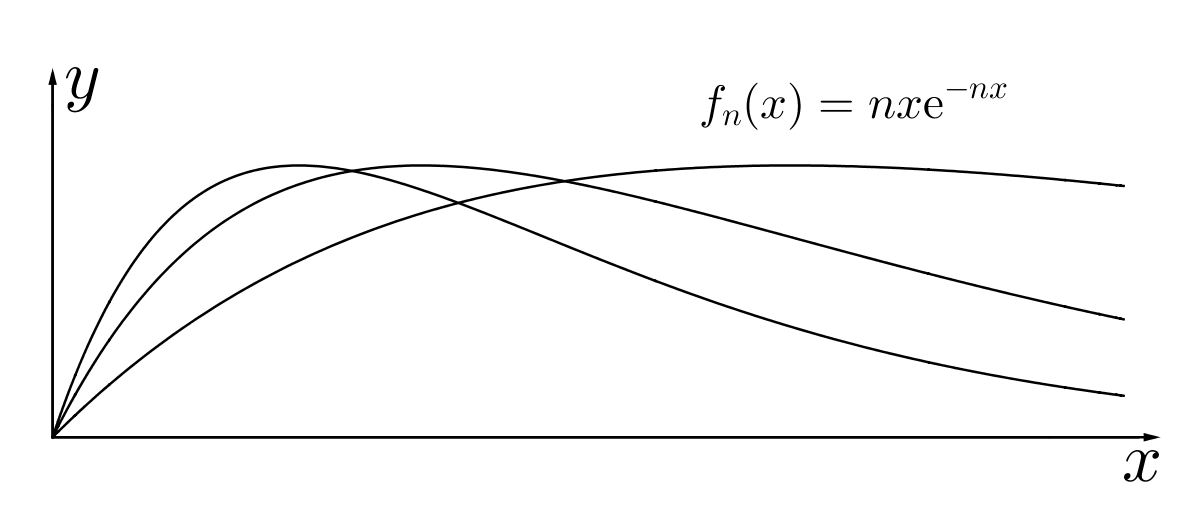
下面三个函数项级数均逐点收敛到 $0$。

$f_n(x) = x \e^{-nx}$ 一致收敛（峰值往左，高度下降）。

$f_n(x) = nx \e^{-nx}$ 不一致收敛，但一致有界（峰值往左，但高度不变）。

$f_n(x) = n^2 x \e^{nx}$ 不一致收敛，也不一致有界（峰值往左，高度也上升）。

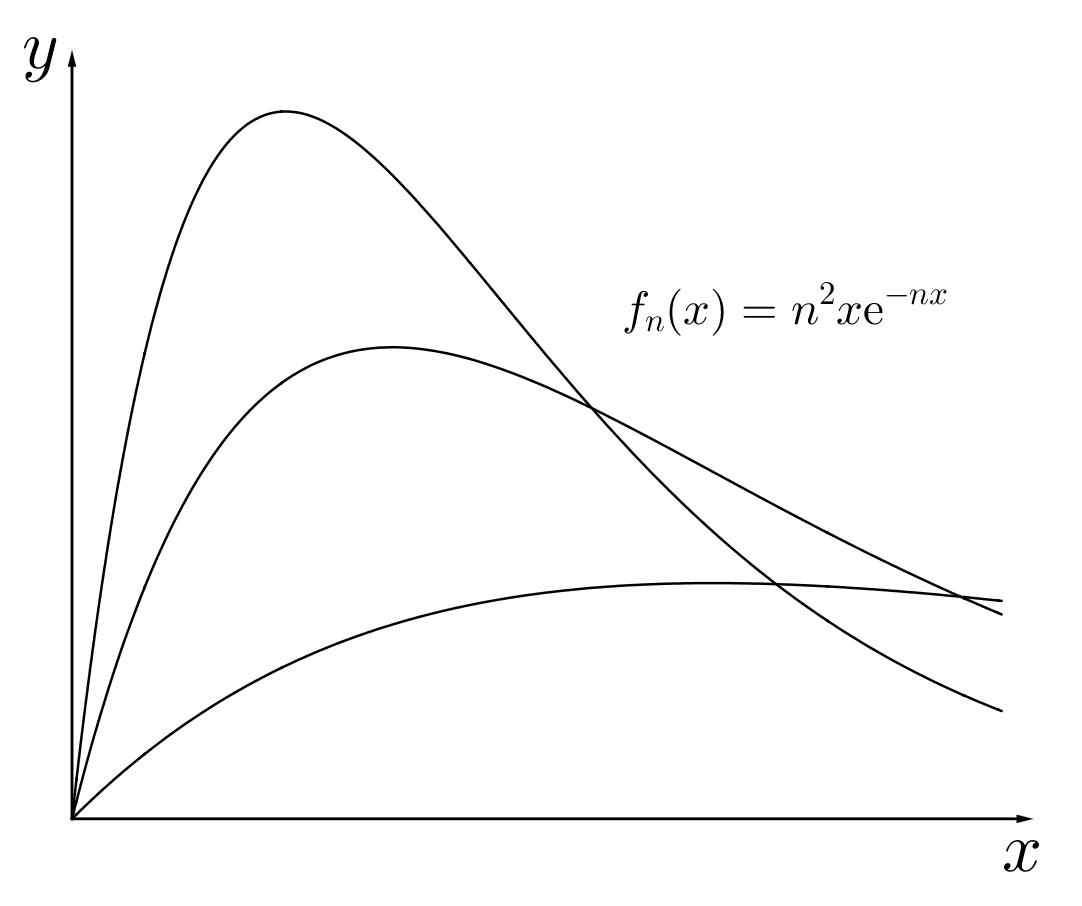
绝对一致收敛

若 $\displaystyle\sum_{n=1}^{\infty} |u_n(x)|$ 在区间 $I$ 上一致收敛，则称函数项级数 $\displaystyle\sum_{n=1}^{\infty} u_n(x)$ 在区间 $I$ 上绝对一致收敛。

绝对一致收敛的函数项级数一定是一致收敛的，但反之不一定成立。

魏尔斯特拉斯判别法（强级数判别法）

设函数项级数 $\displaystyle\sum_{n=1}^{\infty} u_n(x)$ 在区间 $I$ 上，对于任意 $x \in I$，都有 $\left|u_n(x)\right| \le a_n$，且 $\displaystyle\sum_{n=1}^{\infty} a_n$ 收敛，则函数项级数 $\displaystyle\sum_{n=1}^{\infty} u_n(x)$ 在区间 $I$ 上一致收敛。

其中的 $\displaystyle\sum_{n=1}^{\infty} a_n$ 称为函数项级数 $\displaystyle\sum_{n=1}^{\infty} u_n(x)$ 的强级数。

证明

$\displaystyle\sum_{n=1}^{\infty} a_n$ 收敛即 $\displaystyle\sum_{n=1}^{\infty} a_n$ 任意部分和有界。即 $\forall \varepsilon > 0$，都有 $N$ 使得 $\left\lvert \displaystyle \sum_{k=n+1}^{m}a_{k} \right\rvert$ 对任意 $m > n > N$ 成立。

又 $\left\lvert u_{k}(x) \right\rvert \le a_{k}$ 对任意 $x \in I$ 成立，所以

$$\begin{aligned} \left\lvert \sum_{k=n+1}^{m} u_{k}(x) \right\rvert &\le \sum_{k=n+1}^{m} \left\lvert u_{k}(x) \right\rvert\\ &\le \sum_{k=n+1}^{m} a_{k}\\ &< \varepsilon \end{aligned}$$

进而 $\left\lvert \displaystyle \sum_{k=n+1}^{\infty}u_{k}(x) \right\rvert < \varepsilon$ 对任意 $x \in I, n \in \N^{+}$ 成立，即

$$\begin{aligned} \left\lvert r_n(x) \right\rvert &= \left\lvert S(x) - S_n(x) \right\rvert\\ &= \left\lvert \sum_{k=n+1}^{\infty} u_{k}(x) \right\rvert\\ &< \varepsilon \end{aligned}$$

所以函数项级数 $\displaystyle\sum_{n=1}^{\infty} u_n(x)$ 在区间 $I$ 上一致收敛。

若函数项级数 $\displaystyle\sum_{n=1}^{\infty} u_n(x)$ 在 $[a, b]$ 上一致连续，且每一项 $u_n(x)$ 在 $[a, b]$ 上连续，则其和函数 $S(x) = \displaystyle\sum_{n=1}^{\infty} u_n(x)$ 在 $[a, b]$ 上也连续。

证明

$\displaystyle\sum_{n=1}^{\infty} u_n(x) \rightrightarrows S(x)$，对任意 $\varepsilon > 0$，存在 $N = N(\varepsilon)$ 使得 $n > N$ 时，对任意 $x \in [a, b]$ 有

$$\left\lvert S(x) - S_n(x) \right\rvert < r_n(x) < \dfrac{\varepsilon}{3}$$

故对 $[a, b]$ 上一个固定点 $x_0$，也有 $r_n(x_0) < \dfrac{\varepsilon}{3}$。

对选定的 $N$，$S_{N+1}(x)$ 也为在 $x_0$ 连续的函数，故对上面的 $\varepsilon > 0$，存在 $\delta > 0$ 使得当 $\left\lvert x - x_0 \right\rvert < \delta$ 时，有

$$\left\lvert S_{N+1}(x) - S_{N+1}(x_0) \right\rvert < \dfrac{\varepsilon}{3}$$

因此当 $\left\lvert x - x_0 \right\rvert < \delta$ 时，有

$$\begin{aligned} \left\lvert S(x) - S(x_0) \right\rvert &\le \left\lvert S(x) - S_{N+1}(x) \right\rvert + \left\lvert S_{N+1}(x) - S_{N+1}(x_0) \right\rvert + \left\lvert S_{N+1}(x_0) - S(x_0) \right\rvert\\ &< \dfrac{\varepsilon}{3} + \dfrac{\varepsilon}{3} + \dfrac{\varepsilon}{3}\\ &= \varepsilon \end{aligned}$$

逐项积分

如果级数 $\displaystyle\sum_{n=1}^{\infty} u_n(x)$ 的各项 $u_n(x)$ 在区间 $[a, b]$ 连续，且 $\displaystyle\sum_{n=1}^{\infty} u_n(x)$ 在 $[a, b]$ 上一致收敛于 $S(x)$，则级数 $\displaystyle\sum_{n=1}^{\infty} u_n(x)$ 在 $[a, b]$ 上可以逐项积分，即

$$\int_a^b S(x) \d x = \sum_{n=1}^{\infty} \int_a^b u_n(x) \d x$$

证明

$S_n(x) \rightrightarrows S(x)$ 得任意 $\varepsilon > 0$，存在 $N$ 使得 $n > N$ 时，对任意 $x \in [a, b]$ 有 $\left\lvert S(x) - S_n(x) \right\rvert < \dfrac{\varepsilon}{b - a}$。

$$\begin{aligned} \left\lvert \int_a^b S(x) \d x - \sum_{k=1}^{n}u_{k}(x) \d x \right\rvert &= \left\lvert \int_a^b \left(S(x) - \sum_{k=1}^{n}u_k(x)\right) \d x \right\rvert\\ &= \left\lvert \int_a^b \left(S(x) - S_n(x)\right) \d x \right\rvert\\ &\le \int_a^b \left\lvert S(x) - S_n(x)\right\rvert \d x \\ &\le \int_a^b \dfrac{\varepsilon}{b - a} \d x\\ &= \varepsilon \end{aligned}$$

逐项求导

如果级数 $\displaystyle\sum_{n=1}^{\infty} u_n(x)$ 在区间 $[a, b]$ 上一致收敛于 $S(x)$，$u_n(x)$ 的导函数 $u'_n(x)$ 在 $[a, b]$ 上连续，并且级数 $\displaystyle\sum_{n=1}^{\infty} u'_n(x)$ 在 $[a, b]$ 上一致连续，则和函数 $S(x)$ 在区间 $[a, b]$ 上可导，且可逐项求导，即

$$S'(x) = \sum_{n=1}^{\infty} u'_n(x)$$

并且 $S'(x)$ 也在 $[a, b]$ 上连续。

证明

记 $\displaystyle\sum_{n=1}^{\infty} u'_n(x) \rightrightarrows \varphi(x)$，即

$$\varphi(x) = \sum_{n=1}^{\infty} u'_n(x)$$

由逐项积分，取 $x \in [a, b]$，有

$$\begin{aligned} \int_a^x \varphi(t) \d t &= \int_a^x \sum_{n=1}^{\infty} u'_n(t) \d t\\ &= \sum_{n=1}^{\infty} \int_a^x u'_n(t) \d t\\ &= \sum_{n=1}^{\infty} \left(u_n(x) - u_n(a)\right)\\ &= \sum_{n=1}^{\infty} u_n(x) - \sum_{n=1}^{\infty} u_n(a)\\ &= S(x) - S(a) \end{aligned}$$

再由 $u'_n(x)$ 的一致连续性有 $\varphi(x)$ 在 $[a, b]$ 上连续，所以

$$S(x) = S(a) + \int_a^x \varphi(t) \d t$$

可导，且 $S'(x) = \varphi(x) = \displaystyle\sum_{n=1}^{\infty} u'_n(x)$。

幂级数

本节幂级数下标基本从 $n=0$ 开始，与上面有所区别。

幂级数

形如

$$\displaystyle\sum_{n=0}^{\infty} a_n(x - x_0)^n = a_0 + a_1(x - x_0) + a_2(x - x_0)^2 + \cdots$$

的函数项级数称为幂级数。

为简单起见，讨论幂级数时，一般取 $x_0 = 0$，即

$$\displaystyle\sum_{n=0}^{\infty} a_n x^n = a_0 + a_1 x + a_2 x^2 + \cdots$$

阿贝尔定理

对于幂级数 $\displaystyle\sum_{n=0}^{\infty} a_nx^n$，有

1. 若此级数在 $x_1 \ne 0$ 处收敛，则对任意满足 $|x| < |x_1|$ 的 $x$，都有 $\displaystyle\sum_{n=0}^{\infty} a_nx^n$ 在 $x$ 处绝对收敛。
2. 若此级数在 $x_2 \ne 0$ 处发散，则对任意满足 $|x| > |x_2|$ 的 $x$，都有 $\displaystyle\sum_{n=0}^{\infty} a_nx^n$ 在 $x$ 处发散。

即幂级数收敛域除端点外是关于 $x = 0$ 对称的。

证明

既然 $\displaystyle\sum_{n=0}^{\infty} a_nx_1^n$ 收敛，所以 $\lim\limits_{n \to \infty} a_nx_1^n = 0$，从而数列 $\left\lbrace a_nx_1^n \right\rbrace$ 有界，即存在 $M > 0$ 使

$$\left\lvert a_n x_1^n \right\rvert \le M$$

于是对任意一个满足 $|x| < |x_1|$ 的 $x$，有

$$\begin{aligned} \left\lvert a_n x^n \right\rvert &= \left\lvert a_n x_1^n \right\rvert \left\lvert \dfrac{x}{x_1} \right\rvert^n\\ &\le M \left\lvert \dfrac{x}{x_1} \right\rvert^n \end{aligned}$$

又 $\left\lvert \dfrac{x}{x_1} \right\rvert < 1$，因此等比数列 $\displaystyle\sum_{n=0}^{\infty} \left\lvert \dfrac{x}{x_1} \right\rvert^n$ 收敛。

比较判别法知 $\displaystyle\sum_{n=0}^{\infty} \left\lvert a_nx^n \right\rvert$ 收敛，即 $\displaystyle\sum_{n=0}^{\infty} a_nx^n$ 绝对收敛。

第二个结论可由第一个结论推出：反证法，设 $|x| > |x_2|$ 时级数收敛，由第一个结论知 $|x_2| < |x|$，级数在 $x_2$ 处收敛，矛盾。

柯西-阿达马定理/阿贝尔第一定理（Cauchy-Hadamard/Abel）

对幂级数 $\displaystyle\sum_{n=0}^{\infty} a_nx^n$，存在 $0 \le R \le +\infty$，使得

1. 当 $|x| < R$ 时，级数绝对收敛；
2. 当 $|x| > R$ 时，级数发散；
3. 当 $|x| = R$ 时，级数可能收敛，可能发散。

$R$ 称为幂级数的收敛半径，开区间 $(-R, R)$ 称为幂级数的收敛区间，所有收敛点的集合称为幂级数的收敛域。

也就是说收敛区间与收敛域未必相同。

达朗贝尔判别法（D'Alembert）

对于幂级数 $\displaystyle\sum_{n=0}^{\infty} a_n x^n$，若

$$\lim\limits_{n \to \infty} \left\lvert \dfrac{a_{n+1}}{a_n} \right\rvert = l$$

则级数的收敛半径

$$R = \begin{cases} \dfrac{1}{l} & 0 < l < + \infty\\ 0 & l = +\infty\\ +\infty & l = 0 \end{cases}$$

证明

$x = 0$ 时显然，不妨设 $x \ne 0$，则有

$$\lim_{n\to \infty }\left\lvert \dfrac{a_{n+1}x^{n+1}}{a_nx^n} \right\rvert = \lim_{n\to \infty }\left\lvert \dfrac{a_{n+1}}{a_n} \right\rvert |x| = \begin{cases} l|x| & 0 < l < +\infty\\ 0 & l = 0\\ +\infty & l = +\infty \end{cases}$$

若 $0 < l < + \infty$，当 $|x| < \dfrac{1}{l}$ 时，级数 $\displaystyle\sum_{n=0}^{\infty} a_n x^n$ 绝对收敛，当 $|x| > \dfrac{1}{l}$ 时，级数发散。故 $R = \dfrac{1}{l}$。

若 $l = 0$，则级数 $\displaystyle\sum_{n=0}^{\infty} a_n x^n$ 对任意 $x$ 都绝对收敛，故 $R = +\infty$。

若 $l = +\infty$，则级数 $\displaystyle\sum_{n=0}^{\infty} a_n x^n$ 对任意 $x$ 都发散，故 $R = 0$。

柯西判别法

对于幂级数 $\displaystyle\sum_{n=0}^{\infty} a_n x^n$，若

$$\lim\limits_{n \to \infty} \sqrt[n]{\left\lvert a_n \right\rvert} = l$$

则级数的收敛半径

$$R = \begin{cases} \dfrac{1}{l} & 0 < l < + \infty\\ 0 & l = +\infty\\ +\infty & l = 0 \end{cases}$$

设幂级数 $\displaystyle\sum_{n=0}^{\infty} a_nx^n$ 与 $\displaystyle\sum_{n=0}^{\infty} b_nx^n$ 收敛半径分别为 $R_1, R_2$，令 $R = \min\left\lbrace R_1, R_2 \right\rbrace$，则对于 $|x| < R$，有

1. $\displaystyle\sum_{n=0}^{\infty} (a_n \pm b_n)x^n = \displaystyle\sum_{n=0}^{\infty} a_nx^n \pm \displaystyle\sum_{n=0}^{\infty} b_nx^n$；
2. $\displaystyle\sum_{n=0}^{\infty} c_nx^n = \left(\displaystyle\sum_{n=0}^{\infty} a_nx^n\right) \cdot \left(\displaystyle\sum_{n=0}^{\infty} b_nx^n\right)$。
   • 其中 $c_n = a_0b_n + a_1b_{n-1} + \cdots + a_nb_0$；
3. $b_0 \ne 0$ 时，在 $x = 0$ 的适当邻域内，两幂级数可以相除，即 $\displaystyle\sum_{n=0}^{\infty} c_nx^n = \dfrac{\displaystyle\sum_{n=0}^{\infty} a_nx^n}{\displaystyle\sum_{n=0}^{\infty} b_nx^n}$。
   • 系数可由 $\displaystyle\sum_{n=0}^{\infty} a_nx^n = \left(\displaystyle\sum_{n=0}^{\infty} b_nx^n\right) \cdot \left(\displaystyle\sum_{n=0}^{\infty} c_nx^n\right)$ 依次确定。
   • 收敛区间可能比原来两级数的收敛半径小

内闭一致收敛性（阿贝尔第二定理）

设幂级数 $\displaystyle\sum_{n=0}^{\infty} a_nx^n$ 收敛半径 $R > 0$，收敛域为 $X$，任取闭区间 $[a, b] \subseteq X$，则有该幂级数在 $[a, b]$ 上一致收敛。

幂级数 $\displaystyle\sum_{n=0}^{\infty} a_nx^n$ 的和函数 $S(x)$ 在其收敛域 $I$ 上连续。

特别地，若 $\displaystyle\sum_{n=0}^{\infty} a_nx^n$ 在 $R$ 处收敛，则 $S(x)$ 在 $R$ 处左连续，若其在 $-R$ 处收敛，则 $S(x)$ 在 $-R$ 处右连续。

幂级数 $\displaystyle\sum_{n=0}^{\infty} a_nx^n$ 的和函数 $S(x)$ 在其收敛域 $I$ 上可逐项积分，且有逐项积分公式

$$\begin{aligned} \int_0^x S(t) \d t &= \int_0^x \left( \displaystyle\sum_{n=0}^{\infty} a_nt^n \right) \\ &= \displaystyle\sum_{n=0}^{\infty} \int_0^x a_nt^n \d t\\ &= \displaystyle\sum_{n=0}^{\infty} \dfrac{a_n}{n+1} x^{n+1} \end{aligned}$$

幂级数 $\displaystyle\sum_{n=0}^{\infty} a_nx^n$ 的和函数 $S(x)$ 在其收敛域 $I$ 上可逐项求导，且有逐项求导公式

$$\begin{aligned} S'(x) &= \left( \displaystyle\sum_{n=0}^{\infty} a_nx^n \right)'\\ &= \displaystyle\sum_{n=0}^{\infty} \left( a_nx^n \right)'\\ &= \displaystyle\sum_{n=1}^{\infty} na_nx^{n-1} \end{aligned}$$

求幂级数 $\displaystyle\sum_{n=1}^{\infty} \dfrac{1}{n} x^n$，并计算 $\displaystyle\sum_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{n}$。

---

考虑具体一个例子，来看看过程。

过程

$$\begin{aligned} l &= \lim\limits_{n \to \infty} \left| \dfrac{a_{n+1}}{a_n} \right| \\ &= \lim\limits_{n \to \infty} \left| \dfrac{1}{n+1} \cdot \dfrac{n}{1} \right| \\ &= 1 \end{aligned}$$

从而收敛半径 $R = \dfrac{1}{l} = 1$。

$x = 1$ 时，幂级数为调和级数，发散；$x = -1$ 时，莱布尼茨判别法知收敛，故收敛域为 $[-1, 1)$。

内闭一致收敛性有，对 $x \in [-1, 1)$ 有

$$\begin{aligned} S(x) &= \sum_{n=1}^{\infty} \dfrac{1}{n} x^n \\ S'(x) &= \sum_{n=1}^{\infty} x^{n-1} \\ &= \sum_{n=0}^{\infty} x^{n} \end{aligned}$$

随即对 $x \in (-1, 1)$，有 $S'(x) = \dfrac{1}{1 - x}$，从而有

$$\begin{aligned} S(x) &= S(x) - S(0)\\ &= \int_0^x S'(t) \d t\\ &= -\ln(1 - x) + C \end{aligned}$$

代入 $x = 0$，得 $C = 0$，从而有 $S(x) = -\ln(1 - x)$。

内闭一致收敛性有 $S(x)$ 在 $-1$ 处右连续，从而

$$\begin{aligned} \displaystyle\sum_{n=1}^{\infty} (-1)^{n-1} \dfrac{1}{n} &= - S(-1)\\ &= -\lim\limits_{x \to -1^{+}} S(x) \\ &= \ln 2 \end{aligned}$$

泰勒级数

既然幂级数可以收敛到一个和函数，能否将一个函数展开成幂级数呢？

假设 $f(x)$ 在点 $x_0$ 的某邻域 $N_{\delta}(x_0)$ 内能展成幂级数，即有

$$f(x) = \sum_{n=0}^{\infty} a_n (x - x_0)^n\qquad x \in N_{\delta}(x_0)$$

显然 $f(x)$ 在 $N_{\delta}(x_0)$ 内有无穷阶导数，且有

$$f^{(n)}(x_0) = n! a_n$$

亦即展开式必为

$$\sum_{n=0}^{\infty} \dfrac{f^{(n)}(x_0)}{n!} (x - x_0)^n$$

该幂级数称为 $f(x)$ 在 $x_0$ 处的泰勒级数。

$$f(x) = \sum_{n=0}^{\infty} \dfrac{f^{(n)}(x_0)}{n!} (x - x_0)^n$$

称为 $f(x)$ 在 $x_0$ 处的泰勒展开式。

从而 $f(x)$ 在 $N_{\delta}(x_0)$ 内可展成幂级数的充要条件是 $f(x)$ 在 $N_{\delta}(x_0)$ 内有无穷阶导数，且级数在 $N_{\delta}(x_0)$ 内收敛到 $f(x)$。

设 $f(x)$ 在点 $x_0$ 的某个邻域 $N_{\delta}$ 内有任意阶导数，则 $f(x)$ 在该邻域内能展成泰勒级数的充要条件为

$$\lim\limits_{n \to \infty}R_n(x) = 0\qquad x \in N_{\delta}(x_0)$$

这里 $R_n(x)$ 为泰勒级数的余项。

将 $f(x)$ 展开为泰勒级数步骤：

1. 求出 $f^{(n)}(x_0)$，若存在 $n$ 使得 $f^{(n)}(x_0)$ 不存在，则 $f(x)$ 在 $x_0$ 处不能展成泰勒级数。
2. 写出幂级数 $\displaystyle \sum_{n=0}^{\infty} \dfrac{f^{(n)}(x_0)}{n!} (x - x_0)^n$，并求出收敛半径 $R$。
3. 利用余项 $R_n(x)$ 表达式，考察 $x \in N_{R}(x_0)$ 时，余项 $R_n(x)$ 极限是否为零。若为零，则展开式为泰勒级数。
   • $R_n(x) = \dfrac{f^{(n+1)}(\xi)}{(n + 1)!}(x - x_0)^{n+1}$，其中 $\xi$ 在 $x_0$ 和 $x$ 之间。

各种余项：

• 皮亚诺余项：$R_n(x) = o\left((x - x_0)^n\right)$。
• 拉格朗日余项：$R_n(x) = \dfrac{f^{(n+1)}(\xi)}{(n + 1)!}(x - x_0)^{n+1}$，其中 $\xi$ 在 $x_0$ 和 $x$ 之间。
• 柯西余项：$R_n(x) = \dfrac{f^{(n+1)}(\theta x)}{n!}(1 - \theta)^nx^{n+1}$，其中 $\theta \in (0, 1)$。

二项式级数（$m \notin \N$）：

$$\begin{aligned} (1 + x)^m &= \sum_{n=0}^{\infty} \binom{m}{n}x^n\\ &= 1 + \sum_{n=1}^{\infty} \frac{m(m-1)\cdots(m-n+1)}{n!}x^n\\ &= 1 + \sum_{n=1}^{\infty} \dfrac{x^n}{n !} \displaystyle \prod_{i=0}^{n-1}(m - i) \end{aligned}$$

收敛域需分类讨论：

1. $m > 0$：$[-1, 1]$
2. $-1 < m < 0$：$(-1, 1]$
3. $m \le -1$：$(-1, 1)$

---

讨论

1. $m > 0$：

2. $-1 < m < 0$：

$x = -1$ 时，$n > 0$ 时有

$$\begin{aligned} (-1)^n \dbinom{m}{n} &= \prod_{i=0}^{n-1}\dfrac{|m| + i}{i + 1}\\ &= \dfrac{|m|}{1} \dfrac{|m| + 1}{2} \cdots \dfrac{|m| + n - 1}{n}\\ &= \dfrac{|m|}{n} \dfrac{|m| + 1}{1} \cdots \dfrac{|m| + n - 1}{n - 1}\\ &\ge \dfrac{|m|}{n} \end{aligned}$$

即 $\left\lvert \dbinom{m}{n} \right\rvert \ge \dfrac{|m|}{n}$，故级数发散。

$x = 1$ 时，$\displaystyle \sum_{n=1}^{\infty}\displaystyle \dbinom{m}{n} = \sum_{n=1}^{\infty} \dfrac{1}{n!} \prod_{i=0}^{n-1}(m-i)$ 为交错级数。而

$$\begin{aligned} \dbinom{m}{n} &= \dfrac{1}{n!}\left\lvert \prod_{i=0}^{n-1}(m-i) \right\rvert \\ &> \dfrac{1}{n!}\left\lvert \prod_{i=0}^{n-1}(m-i) \right\rvert \left\lvert \dfrac{m - n}{n + 1} \right\rvert\\ &= \dfrac{1}{(n+1)!} \left\lvert \prod_{i=0}^{n}(m - i) \right\rvert\\ &= \left\lvert \dbinom{m}{n + 1} \right\rvert \end{aligned}$$

即 $\left\lbrace \left\lvert \dbinom{m}{n} \right\rvert \right\rbrace$ 是递减数列，莱布尼茨判别法知 $\displaystyle \sum_{n=1}^{\infty} \dfrac{1}{n !} \displaystyle \prod_{i=0}^{n-1}(m - i)$，故级数收敛。

3. $m \le -1$：

$x = \pm 1$ 时，$n > 0$ 时有

$$\begin{aligned} \left\lvert \dbinom{m}{n} \right\rvert &= \left\lvert \prod_{i=0}^{n-1} \dfrac{m - i}{i + 1} \right\rvert\\ &= \prod_{i=0}^{n-1} \dfrac{i - m}{i + 1}\\ &\ge 1 \end{aligned}$$

即 $\left\lvert \dbinom{m}{n} \ge 1 \right\rvert$，故级数发散。

广义积分的敛散性

柯西收敛原理

广义积分 $\displaystyle\int_{a}^{\infty}f(x)\d x$ 收敛的充要条件是：对任意 $\varepsilon > 0$，存在 $R > a$，使得当 $A_1, A_2 > R$ 时，恒有

$$\left\lvert \int_{A_1}^{A_2}f(x)\d x \right\rvert < \varepsilon$$

若广义积分 $\displaystyle\int_{a}^{\infty}|f(x)|\d x$ 收敛，则称广义积分 $\displaystyle\int_{a}^{\infty}f(x)\d x$ 绝对收敛；若 $\displaystyle\int_{a}^{\infty}f(x)\d x$ 收敛而 $\displaystyle\int_{a}^{\infty}|f(x)|\d x$ 发散，则称 $\displaystyle\int_{a}^{\infty}f(x)\d x$ 条件收敛。

若 $f(x)$ 是 $[a, \infty )$ 上的非负可积函数，则 $\displaystyle\int_{a}^{\infty}f(x)\d x$ 收敛的充要条件是：函数 $F(x) = \displaystyle \int_a^x f(t) \d t$ 在 $[a, \infty)$ 上有上界。

比较判别法

设函数 $f(x), g(x)$ 在区间 $[a, \infty )$ 上有定义，且

$$0 \le f(x) \le g(x) \quad (x \ge a)$$

并设 $b \ge a$ 时，$f(x), g(x)$ 在任意区间 $[a, b]$ 上可积，则有：

1. $\displaystyle\int_{a}^{\infty} g(x) \d x$ 收敛时，$\displaystyle\int_{a}^{\infty} f(x) \d x$ 收敛；
2. $\displaystyle\int_{a}^{\infty} f(x) \d x$ 发散时，$\displaystyle\int_{a}^{\infty} g(x) \d x$ 发散。

比较判别法极限形式

设函数 $f(x), g(x)$ 在区间 $[a, \infty )$ 上有定义，$f(x) \ge 0, g(x) > 0$，

并设 $b \ge a$ 时，$f(x), g(x)$ 在任意区间 $[a, b]$ 上可积，且

$$\lim_{x \to \infty} \dfrac{f(x)}{g(x)} = \lambda$$

则：

1. $0 \le \lambda < \infty$：$\displaystyle\int_{a}^{\infty} g(x) \d x$ 收敛时，$\displaystyle\int_{a}^{\infty} f(x) \d x$ 收敛；
2. $0 < \lambda \le \infty$：$\displaystyle\int_{a}^{\infty} g(x) \d x$ 发散时，$\displaystyle\int_{a}^{\infty} f(x) \d x$ 发散。

特别地，$0 < \lambda < \infty$ 时，两个广义积分同敛散。

柯西判别法

设 $f(x) \ge 0$，$x \in [a, \infty )$，若

$$\lim\limits_{x \to \infty} x^p f(x) = \lambda$$

则：

1. $0 \le \lambda < \infty$：$p > 1$ 时，$\displaystyle\int_{a}^{\infty} f(x) \d x$ 收敛；
2. $0 < \lambda \le \infty$：$p \le 1$ 时，$\displaystyle\int_{a}^{\infty} f(x) \d x$ 发散。

狄利克雷判别法

设 $f(x), g(x)$ 在区间 $[a, \infty )$ 上有定义，且

1. 对任意 $b \ge a$，积分 $\displaystyle\int_{a}^{b} f(x) \d x$ 有界；
2. 函数 $g(x)$ 在 $[a, \infty )$ 上单调递减且趋于零。

则广义积分 $\displaystyle\int_{a}^{\infty} f(x)g(x) \d x$ 收敛。

阿贝尔判别法

设 $f(x), g(x)$ 在区间 $[a, \infty )$ 上有定义，且

1. 广义积分 $\displaystyle\int_{a}^{\infty} f(x)\d x$ 收敛；
2. 函数 $g(x)$ 在 $[a, \infty )$ 上单调有界。

则广义积分 $\displaystyle\int_{a}^{\infty} f(x)g(x) \d x$ 收敛。

无界积分有类似判别法与定理等，不再赘述。

特殊函数

$\Gamma$ 函数

欧拉积分

含参 $s$ 的广义积分

$$\int_{0}^{\infty} t^{s-1}\e^{-t} \d t$$

称为第二类欧拉积分。这也是 Gamma 函数 $\Gamma$ 的定义

$$\Gamma(s) = \int_{0}^{\infty} t^{s-1}\e^{-t} \d t$$

$\Gamma$ 函数有性质

$$\Gamma(s+1) = s\Gamma(s)$$

---

$$\begin{aligned} \Gamma(s+1) &= \int_{0}^{\infty} t^{s}\e^{-t} \d t\\ &= -t^s \e^{-t} \as_{0}^{\infty} + s\int_{0}^{\infty} t^{s-1}\e^{-t} \d t\\ &= s\Gamma(s) \end{aligned}$$

因此 $\Gamma$ 函数可以看作是阶乘的推广，即

$$\Gamma(n) = (n-1)!$$

$\Gamma$ 函数及其任意阶导数在 $(0, \infty )$ 连续，且

$$\Gamma^{(n)}(s) = \int_{0}^{\infty} t^{s-1}\e^{-t}(\ln t)^n \d t$$

余元公式

对 $s \in (0, 1)$ 有

$$\Gamma(s)\Gamma(1-s) = \dfrac{\pi}{\sin \pi s}$$

从而得到

$$\Gamma\left(\dfrac{1}{2}\right) = \sqrt{\pi}$$

$\Beta$ 函数

含参 $x, y$ 的积分

$$\int_0^1 t^{x-1}(1-t)^{y-1} \d t$$

• 当 $x \ge 1, y \ge 1$ 时，为定积分
• $x < 1$ 时，$t = 0$ 为奇点
• $y < 1$ 时，$t = 1$ 为奇点

并记

$$\Beta(x, y) = \int_0^1 t^{x-1}(1-t)^{y-1} \d t$$

为 Beta 函数 $\Beta$。

$\Beta$ 函数及其任意阶导数在 $(0, \infty )^2$ 连续，且

$$\Beta(x, y) = \dfrac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}$$

$$\Beta(p, q + 1) = \dfrac{q}{p + q}\Beta(p, q)\\ \Beta(p + 1, q) = \dfrac{p}{p + q}\Beta(p, q)$$

则 $m, n$ 为自然数时有

$$\begin{aligned} \Beta(m, n) &= \dfrac{\Gamma(m)\Gamma(n)}{\Gamma(m + n)}\\ &= \dfrac{(m-1)!(n-1)!}{(m+n-1)!} \end{aligned}$$

计算

$$I = \int_0^{\frac{\pi}{2}} \sin^n x \d x$$

---

过程

记

$$\left\lbrace\begin{aligned} x &= \dfrac{n + 1}{2}\\ y &= \dfrac{1}{2} \end{aligned}\right.$$

$$\begin{aligned} I &= \dfrac{1}{2} \Beta\left(\dfrac{n + 1}{2}, \dfrac{1}{2}\right)\\ &= \dfrac{1}{2} \dfrac{\Gamma\left(\dfrac{n + 1}{2}\right)\Gamma\left(\dfrac{1}{2}\right)}{\Gamma\left(\dfrac{n + 1}{2} + \dfrac{1}{2}\right)}\\ &= \begin{cases} \dfrac{(n-1)!!}{n!!} \dfrac{\pi}{2}, & n \text{ 为偶数}\\ \dfrac{(n-1)!!}{n!!}, & n \text{ 为奇数} \end{cases} \end{aligned}$$

傅里叶级数

三角级数与三角函数系的正交性

$$1, \cos x, \sin x, \cdots, \cos nx, \sin nx, \cdots$$

称为基本三角函数系。有如下关系^[2]

$$\begin{aligned} \int_{- \pi}^{\pi} \sin nx \d x &= 0\\ \int_{- \pi}^{\pi} \cos nx \d x &= 0\\ \int_{- \pi}^{\pi} \sin mx \cos nx \d x &= 0\\ \int_{- \pi}^{\pi} \sin mx \sin nx \d x &= 0\quad (m \ne n)\\ \int_{- \pi}^{\pi} \cos mx \cos nx \d x &= 0\quad (m \ne n) \end{aligned}$$

即三角函数系在区间 $[-\pi, \pi]$ 上，在「某种含义上」是正交的。

区间 $[-\pi, \pi]$ 上全体有界可积函数组成的集合 $A$ 在函数的加法及实数的乘法运算下，构成一个线性空间。

内积

对该线性空间中任意两个函数 $f, g$，定义内积为

$$(f, g) = \dfrac{1}{\pi} \int_{-\pi}^{\pi} f(x) g(x) \d x$$

并定义

范数

$$\|f\| = \sqrt{(f, f)} = \sqrt{\dfrac{1}{\pi} \int_{-\pi}^{\pi} f^{2}(x) \d x}$$

为函数 $f$ 的范数。

$A$ 称为赋范线性空间。

两向量 $f, g$ 正交，指它们的内积为 $0$，函数系正交，即函数系中任意两个不同元素的内积为 $0$。

而注意到

$$\begin{aligned} \int_{- \pi}^{\pi} \d x &= 2 \pi\\ \int_{- \pi}^{\pi} \sin^{2} nx \d x &= \pi\\ \int_{- \pi}^{\pi} \cos^{2} nx \d x &= \pi \end{aligned}$$

因此函数系

$$\dfrac{1}{\sqrt{2}}, \cos x, \sin x, \cdots, \cos nx, \sin nx, \cdots$$

不仅正交，而且每个元素范数为 $1$。因此这个函数系称为单位正交系。

展开成傅里叶级数

以 $A_{k} \sin(k x + \varphi_{k})$ 为项作成的无穷级数

$$\sum_{k=0}^{\infty} A_{k} \sin(k x + \varphi_{k})$$

称为三角级数。显然级数在长度为 $2 \pi$ 的闭区间收敛，和函数 $f(x)$ 是一个周期函数。

$A_n \sin(n x + \varphi_n)$ 可以展开为

$$A_n \sin(n x + \varphi_n) = A_n \sin \varphi_n \cos nx + A_n \cos \varphi_n \sin nx$$

令

$$\left\lbrace\begin{aligned} \dfrac{a_0}{2} &= A_0 \sin \varphi_0\\ a_n &= A_n \sin \varphi_n\\ b_n &= A_n \cos \varphi_n \end{aligned}\right.$$

则 $n$ 阶三角多项式可写为

$$\dfrac{a_0}{2} + \sum_{k=1}^{\infty} (a_k \cos kx + b_k \sin kx)$$

设函数 $f(x)$ 可展开为三角级数

$$f(x) = \dfrac{a_0}{2} + \sum_{k=1}^{\infty} (a_k \cos kx + b_k \sin kx)$$

则期望求得系数 $a_0, a_1, b_1, \cdots$ 与函数 $f(x)$ 的关系。设级数一致收敛于 $f(x)$，则

$$\int_{- \pi}^{\pi} f(x) \d x = \dfrac{a_0}{2} \cdot 2 \pi = a_0 \pi$$

即

$$a_0 = \dfrac{1}{\pi} \int_{- \pi}^{\pi} f(x) \d x$$

类似线代中的「选择」方法：对某个向量 $\bm{v}$，为选取其第 $i$ 个分量，将其与对应的基向量 $\bm{e}_i$ 进行内积 $\bm{v} \boldsymbol{\cdot} \bm{e}_i$，从而得到系数。

因此套用这个方法，有

$$\begin{aligned} a_n &= \left(f(x), \cos nx\right)\\ &= \dfrac{1}{\pi} \int_{- \pi}^{\pi} f(x) \cos nx \d x \end{aligned}$$

$$\begin{aligned} b_n &= \left(f(x), \sin nx\right)\\ &= \dfrac{1}{\pi} \int_{- \pi}^{\pi} f(x) \sin nx \d x \end{aligned}$$

取 $\dfrac{a_0}{2} = A_0 \sin \varphi_0$ 也有简化系数表示的意义所在。

从而有

欧拉-傅里叶公式

$$\left\lbrace\begin{aligned} a_n &= \dfrac{1}{\pi} \displaystyle \int_{-\pi}^{\pi} f(x) \cos nx \d x,\quad (n = 0, 1, 2, \cdots)\\ b_n &= \dfrac{1}{\pi} \displaystyle \int_{-\pi}^{\pi} f(x) \sin nx \d x,\quad (n = 1, 2, \cdots) \end{aligned}\right.$$

$a_0, a_1, b_1, \cdots$ 称为函数 $f(x)$ 的傅里叶系数（Fourier），三角级数

$$\dfrac{a_0}{2} + \sum_{k=1}^{\infty} (a_k \cos kx + b_k \sin kx)$$

称为 $f(x)$ 的傅里叶级数，记为

$$f(x) \sim \dfrac{a_0}{2} + \sum_{k=1}^{\infty} (a_k \cos kx + b_k \sin kx)$$

不用 $=$，而用 $\sim$ 的原因是因为傅里叶级数不一定收敛于原函数。

狄利克雷收敛定理

设 $f(x)$ 是周期为 $2 \pi$ 的周期函数，若

1. $f(x)$ 在 $[-\pi, \pi]$ 上连续或只有有限个第一类间断点
2. $f(x)$ 在 $[-\pi, \pi]$ 上至多只有有限个严格极值点，即 $f(x)$ 在 $[-\pi, \pi]$ 上分段单调

则 $f(x)$ 的傅里叶级数收敛，且傅里叶级数 $S(x)$ 有

$$S(x) = \begin{cases} f(x), & x \text{ 为 } f(x) \text{ 的连续点}\\ \dfrac{f(x^{+})+f(x^{-})}{2}, & x \text{ 为 } f(x) \text{ 的间断点} \end{cases}$$

若 $f(x)$ 是偶函数，则

$$\begin{aligned} b_n &= \dfrac{1}{\pi} \int_{- \pi}^{\pi} f(x) \sin nx \d x\\ &= 0 \end{aligned}$$

此时 $f(x)$ 的傅里叶级数仅含余弦函数，即

$$f(x) \sim \dfrac{a_0}{2} + \sum_{k=1}^{\infty} a_k \cos kx$$

称为余弦级数。

若 $f(x)$ 是奇函数，则

$$\begin{aligned} a_n &= \dfrac{1}{\pi} \int_{- \pi}^{\pi} f(x) \cos nx \d x\\ &= 0 \end{aligned}$$

此时 $f(x)$ 的傅里叶级数仅含正弦函数，即

$$f(x) \sim \sum_{k=1}^{\infty} b_k \sin kx$$

称为正弦级数。

设定义域为 $\R$ 的周期函数 $f(x)$ 在 $x \in [-\pi, \pi]$ 时有 $f(x) = x^2$，求 $\displaystyle \sum_{n=1}^{\infty}\dfrac{1}{n^2}$ 与 $\displaystyle \sum_{n=1}^{\infty}(-1)^{n-1} \dfrac{1}{n^2}$。

---

过程

由于 $f(x)$ 是偶函数，因此只含余弦级数。由傅里叶级数的定义，有

$$\begin{aligned} a_0 &= \dfrac{1}{\pi} \int_{-\pi}^{\pi} f(x) \d x\\ &= \dfrac{2}{\pi} \int_{0}^{\pi} x^2 \d x\\ &= \dfrac{2}{3} \pi^2 \end{aligned}$$

$$\begin{aligned} a_n &= \dfrac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos nx \d x\\ &= \dfrac{2}{\pi} \int_{0}^{\pi} x^2 \cos nx \d x\\ &= \dfrac{2}{\pi} \int_0^{\pi} \dfrac{x^2}{n} \d \sin nx\\ &= \dfrac{2}{n\pi} \left(x^2 \sin nx \as_0^{\pi} - \int_0^{\pi} 2x \sin nx \d x\right)\\ &= \dfrac{4}{n^2 \pi} \int_0^{\pi} x \d \cos nx\\ &= \dfrac{4}{n^2 \pi} \left(x \cos nx \as_0^{\pi} - \int_0^{\pi} \cos nx \d x\right)\\ &= \dfrac{4}{n^2 \pi} \cdot (-1)^n \pi\\ &= \dfrac{4}{n^2}(-1)^n \end{aligned}$$

狄利克雷收敛定理有

$$x^2 = \dfrac{\pi^2}{3} + \sum_{n=1}^{\infty} \dfrac{4}{n^2}(-1)^n \cos nx$$

因此取 $x = \pi$ 有

$$\pi^2 = \dfrac{\pi^2}{3} + \sum_{n=1}^{\infty} \dfrac{4}{n^2}$$

即

$$\sum_{n=1}^{\infty} \dfrac{1}{n^2} = \dfrac{\pi^2}{6}$$

这也是巴塞尔问题的解。

取 $x = 0$ 有

$$0 = \dfrac{\pi^2}{3} + \sum_{n=1}^{\infty} (-1)^n \dfrac{4}{n^2}$$

即

$$\sum_{n=1}^{\infty} (-1)^{n-1}\dfrac{1}{n^2} = \dfrac{\pi^2}{12}$$

任意周期的周期函数的傅里叶级数

设周期为 $2l$ 的周期函数 $f(x)$ 满足狄利克雷收敛定理的条件，则 $f(x)$ 的傅里叶级数

$$\dfrac{a_0}{2} + \sum_{n=1}^{\infty} \left(a_n \cos \dfrac{n \pi x}{l} + b_n \sin \dfrac{n \pi x}{l}\right)$$

收敛，且

$$S(x) = \begin{cases} f(x), & x \text{ 为 } f(x) \text{ 的连续点}\\ \dfrac{f(x^{+})+f(x^{-})}{2}, & x \text{ 为 } f(x) \text{ 的间断点} \end{cases}$$

其中

$$\left\lbrace\begin{aligned} a_n &= \dfrac{1}{l} \displaystyle \int_{-l}^{l} f(x) \cos \dfrac{n \pi x}{l} \d x,\quad (n = 0, 1, 2, \cdots)\\ b_n &= \dfrac{1}{l} \displaystyle \int_{-l}^{l} f(x) \sin \dfrac{n \pi x}{l} \d x,\quad (n = 1, 2, \cdots) \end{aligned}\right.$$

---

1. 不严谨的写法，仅作为简记。 ↩︎

2. 证明见线代笔记。难怪线代课会讲积分，太愚钝了当时没能注意到这一层联系。 ↩︎