群
群(group)
⟨G,∗⟩ 为群当且仅当 G 有单位元 e 和一元运算 −1 满足:
- G=∅
- ∀x,y∈G,x∗y∈G(代数系统)
- ∀x,y,z∈G,(x∗y)∗z=x∗(y∗z)(半群)
- ∃e∈G,∀x∈G,e∗x=x∗e=x(幺半群)
- ∀x∈G,∃x−1∈G,x∗x−1=x−1∗x=e(群)
2.~5. 为群公理。
等价表述为:设 G 为非空集合,∗ 为 G 上的二元运算,若 ⟨G,∗⟩ 为单元半群,且其单位元有
∀x∈G,∃x−1∈G,x∗x−1=x−1∗x=e
则称 ⟨G,∗⟩ 为群。
群性质:设 ⟨G,∗,e,−1⟩ 为群:
- (a−1)−1=a
- (a∗b)−1=b−1∗a−1
- ab=ac→b=c(左消去律)
- ba=ca→b=c(右消去律)
- ax=b 和 ya=b 在 G 中对 x,y 有唯一解(由消去律可推出)
- 则有限群的运算表中每行(列)均为群中元素的一种排列,且无重复
元素的乘幂(次方)
- a0=e
- an+1=an∗a(n 为自然数)
- a−n=(a−1)n(n 为正整数)
元素的阶
设 ⟨G,∗⟩ 为群,a∈G,a 的阶(周期)定义为
∣a∣=min{n∈N+∣an=e}
若这样的 n 不存在,则称 a 的阶为无穷,a 为无限阶元。
- 有限群不存在无限阶元
- 群中元素及其逆元的阶相等
- 有限群中阶大于 2 的元素个数为偶数
- 阶大于 2 的元素有 a=a−1,因此 a,a−1 成对出现,必为偶数个
- 偶数群中阶为 2 的元素个数为奇数(a=a−1)
- 阶小于 2 的元素有偶数个,而阶为 1 的元素只有一个 e
群的阶
对群 ⟨G,∗⟩:
- 若 G 为有限集,则称 G 为有限群,当 ∣G∣=n 时称 ⟨G,∗⟩ 的阶为 n,G 为 n 阶群
- 若 G 为无限集,则称 G 为无限群
若群 ⟨G,∗⟩ 满足交换律(即 ∀x,y∈G,xy=yx,则称 ⟨G,∗⟩ 为交换群(阿贝尔群)。
- 一阶群同构意义下只有一个,G={e}
- 二阶群也只有一个,G={e,a} 乘法表如下
| ∗ |
e |
a |
| e |
e |
a |
| a |
a |
e |
- 三阶群也只有一个,G={e,a,b} 乘法表如下
| ∗ |
e |
a |
b |
| e |
e |
a |
b |
| a |
a |
b |
e |
| b |
b |
e |
a |
四阶群为均阿贝尔群。
四阶群元素阶为 1 或 2 或 4。
证明
设 G={e,a,b,c},即证 ab=ba。
反证法。若 ab=e,则 ba=c,则 aba=ac,从而 ea=ac 得到 c=e,矛盾!
则 ab=c,从而 ba=c,得证。
仅存在两种四阶群。
存在元素阶为 4:G={e,a,a2,a3} 与 ⟨Z4,⊕4⟩ 同构
| ∗ |
e |
a |
b |
c |
| e |
e |
a |
b |
c |
| a |
a |
b |
c |
e |
| b |
b |
c |
e |
a |
| c |
c |
e |
a |
b |
元素阶均不为 4(Klein 四元群):
| ∗ |
e |
a |
b |
c |
| e |
e |
a |
b |
c |
| a |
a |
e |
c |
b |
| b |
b |
c |
e |
a |
| c |
c |
b |
a |
e |
群方程
若代数系统 (G,∗) 为半群,且 G 中方程 ax=b 与 ya=b 有唯一解,则 (G,∗) 为群。
证明
下面的证明为了方便起见,根据结合律省略 ∗。后面可能会做类似的事情。
先证明有左幺元 el∈G 使得 ∀a∈G,ela=a。
取定 b∈G,xb=b 有唯一解,设为 el,对任何 a∈G,下证 ela=a。
由 bx=a 有解,设为 c,则
ela=el(bc)=(elb)c=bc=a
即 el 为左幺元。
然后证明左逆元存在,即 ∀a∈G,∃a−1∈G,a−1a=el。
只需记 a−1 为 ya=el 的唯一解即可。
接着证明左逆元等于右逆元,即 aa−1=el。
因为 a−1∈G,则 ya−1=el 有唯一解 a′,从而 a′a−1=el,则
aa−1=el(aa−1)=(a′a−1)(aa−1)=a′(a−1a)a−1=a′ela−1=a′a−1=el
最后证明左幺元等于右幺元,即 ∀a∈G,ael=a。
ael=a(a−1a)=(aa−1)a=ela=a
因此 (G,∗) 为群。
若 (G,∗) 为半群,存在左单位元,且每个元素都具有左逆元,则 (G,∗) 为群。
证明
设 el 为左单位元,对任意 a∈G,al 为左逆元,即 ala=el。
由于 al∈G,则也存在 a−1∈G 使得 a−1al=el,则
aal=el(aal)=(a−1al)(aal)=a−1(ala)al=a−1elal=a−1al=el
即左逆元等于右逆元,再证明 el 为右单位元即可:任取 a∈G,有
ael=a(ala)=(aal)a=ela=a
综上,(G,∗) 为群。
设 (G,∗) 为有限半群,若 (G,∗) 满足消去律,则 (G,∗) 为群。
即有限代数系统若同时满足结合律和消去律,则必为群。
无限不一定,例如 ⟨Z+,∗⟩ 满足结合律和消去律,但不是群。
证明
设 {a1,⋯,an},∀a,b∈G,即证明 ax=b 有唯一解。
令 aG={aai∣i=1,⋯,n}。
由左消去律,若 aai=aaj,则 i=j,从而 ∣aG∣=n,从而 aG=G。
而 b∈G,故 b∈aG,即有 ai∈G 使得 aai=b,从而 ax=b 有解。
再通过左消去律,解唯一。
同理可用右消去律证明 ya=b 有唯一解,从而 (G,∗) 为群。
子群
定义
设 ⟨G,∗⟩ 是群,H 是 G 的非空子集,若 H 关于 ∗ 运算构成群,即 ⟨H,∗⟩ 也是群,则 H 是 G 的子群,记作 H≤G。
⟨G,∗⟩ 的平凡子群:
- ⟨G,∗⟩
- ⟨{e},∗⟩
判定定理
判定定理一
设 G 是群,H 是 G 的非空子集。则 H 是 G 的子群当且仅当:
- ∀a,b∈H,ab∈H
- ∀a∈H,a−1∈H
证明
必要性显然。
充分性:因为逆元素的存在性和封闭性已给出,只需证明单位元素的存在性。
取 a∈H,因为 a−1∈H,故 e=aa−1∈H
判定定理二
设 G 是群,H 是 G 的非空子集。则 H 是 G 的子群当且仅当:
∀a,b∈H,ab−1∈H
证明
必要性显然。
充分性:
- 单位元素:取 a∈H,有 e=aa−1∈H
- 逆元素:取 a∈H,因为有 e∈H,故 a−1=ea−1∈H
- 封闭性:任取 a,b∈H,因为 b−1∈H(由上一条),故 ab=a(b−1)−1∈H
有限子群
G 是群,H 是 G 的非空有限子集。则 H 是 G 的子群当且仅当:
∀a,b∈H,ab∈H
证明
必要性显然。
充分性:封闭性已给出,只需证明逆元素和单位元素的存在性。
若 H 中仅含 G 中单位元,显然 H 是子群。
否则任取 H 中异于单位元的元素 a,考虑
a1,a2,⋯
由于 H 有限,存在 i<j 使得 ai=aj,因此有
a−1=aj−i−1
因为有
aj−iai=aj=ai
故
e=aj−i
即
aa−1=aj−i=e
生成子群
设 G 是群,a∈G,构造 G 的子集 H 为
H={ak∣k∈Z}
则 H 是 G 的子群,称 H 是由 a 生成的子群,记作 H=⟨a⟩。
阶
还记得群中元素的阶的定义:
元素的阶
设 ⟨G,∗⟩ 为群,a∈G,a 的阶(周期)定义为
∣a∣=min{n∈N+∣an=e}
若这样的 n 不存在,则称 a 的阶为无穷,a 为无限阶元。
对群 G 的有限阶元素 a,b 有如下性质:
- 对任意 k∈Z+,ak=e 当且仅当 ∣a∣ 整除 k。
- ∣a∣=a−1
- ∣ab∣=∣ba∣
- b−1ab=∣a∣
证明
第一二个显然。
第三个,ab 阶有限,设 ∣ab∣=r,则
(ab)r+1=a(ba)rb=ab
则 (ba)r=e,则 ba 阶有限,设为 r′,则 r′∣r,同理 r∣r′,故 r=r′。
第四个,有
b−1ab=b−1(ab)=(ab)b−1=a(bb−1)=∣a∣
中心
设 G 为群,构造 G 的子集 C 为
C={a∈G∣∀x∈G,ax=xa}
则 C 是 G 的子群,称 C 为 G 的中心。
证明
e∈C,故 C 非空。
即证明任意 a,b∈C,有 ab−1∈C,即
ab−1x=xab−1
而
ab−1x=a(x−1b)−1=a(bx−1)−1=a(xb−1)=(ax)b−1=xab−1
陪集
设 G 是群,H 是 G 的子群,a∈G,定义
aH={ah∣h∈H}
为 a 在 H 上的左陪集。同理可定义 Ha 为 a 在 H 上的右陪集。
设 H 是 G 的子群,则 H 的所有左陪集构成 G 的一个划分。
证明
任取 G 中一个元素 a,一定有 a∈aH(因为 e∈H)。
然后证明
∀a,b∈G,((aH=bH)∨(aH∩bH=∅))
设 aH∩bH=∅,即存在 c∈aH∩bH,令 c=ah1=bh2。
则 a=b(h2h1−1),从而 aH⊆bH。同理可证 bH⊆aH,故 aH=bH。
a,b 属于同一个左陪集当且仅当 a∈bH∧b∈aH 或 b−1a∈H。
左陪集关系
设 H 是群 G 的子群,定义 G 上二元关系 R 为:对任意 a,b∈G,aRb⟺b−1a∈H
则 R 是 G 上的等价关系,且 [a]R=aH。
证明
- 自反性:∀a∈G,a−1a=e∈H
- 对称性:a−1b=(b−1a)−1∈H(由自反性)
- 传递性:c−1a=(c−1b)(b−1a)∈H
x∈[a]R⟺aRx⟺x−1a=h∈H⟺x=ah−1∈aH
拉格朗日定理
陪集的势
设 ⟨H,∗⟩≤⟨G,∗⟩,则
H≈aH≈Ha
证明
设 σ:H→aH 为 σ(h)=ah,消去律有 σ 为单射(ah=bh⟹a=b),同时 σ 为满射,则 σ 为双射,故 H≈aH。
对有限群 G,每个陪集元素个数有限且相同,且等于 ∣H∣,即 ∣G∣=k∣H∣,其中 k 为左(右)陪集的个数,称为 H 在 G 中的指数,记为 [G:H]。
拉格朗日定理
设 ⟨G,∗⟩ 为有限群,⟨H,∗⟩≤⟨G,∗⟩,则
∣G∣=∣H∣⋅[G:H]
证明
由 G 有限,故 [G:H] 有限,设为 N。
从而有 a1,⋯,aN∈G 使得 {aiH∣1⩽i⩽N} 为 G 的划分,即
G=i=1⋃NHai
由陪集的势引理,对任意 i,j,有
∣Hai∣=∣Haj∣
则 ∣G∣=∣H∣⋅N,即
∣G∣=∣H∣⋅[G:H]
推论 1
设 ⟨G,∗⟩ 为有限群,a∈G,则 ∣a∣ 为 ∣G∣ 的因子。
证明
显然有 ⟨⟨a⟩,∗⟩≤⟨G,∗⟩,故 ∣⟨a⟩∣ 为 ∣G∣ 的因子。
而 ∣a∣ 有限,故 ∣⟨a⟩∣=∣a∣,即 ∣a∣ 为 ∣G∣ 的因子。
推论 2
设 ⟨G,∗⟩ 为 p 阶群,若 p 为质数,则
∃a∈G,⟨a⟩=G
证明
取 a=e,a∈G,则 ∣⟨a⟩∣ 为 ∣G∣ 的因子,且 ∣⟨a⟩∣⩾2,故 ∣⟨a⟩∣=p,即 G=⟨a⟩。
证明 6 阶群必含 3 阶子群。
证明
拉格朗日定理,G 中元素阶只可能为 1,2,3,6。若 G 中有 6 阶元素,则 b=aa 是 3 阶元素,即 ⟨b⟩ 为 3 阶子群。
若没有 3,6 阶元素,即 ∀x∈G,x2=e,则 ∀x,y∈G,xy=(yx)2(xy)=(yx)(yxxy)=yx,即 G 是交换群,因此 {e,a,b,ab} 构成 4 阶子群,但 4∤6,矛盾。
故 G 中必含 3 阶元素 a 使得 ⟨a⟩ 为 3 阶子群。
考虑模 m 互素同余类 Z/mZ 关于模 m 乘法构成一个群,例如
- Z/6Z={1,5}
- Z/8Z={1,3,5,7}
从而 ∣Z/mZ∣=φ(m) 为 Euler's totient
其构成一个群,封闭性、结合律、单位元 1 显然。
对任意 x,其与 m 互素,裴蜀定理有,存在整数 r,s 使得 xr+ms=1,即 xr=1−ms,从而 xr≡1(modm),从而 rmodm 为 x 的逆。
对任意有限群 G 和其中任意元素 x∈G,有
x∣G∣=e
代入上面的模 m 互素同余群。上面的幂跟实际的幂不一样,上面的幂表示的运算 ∗ 是在「模 m 同余」意义上的。为避免混淆,使用 x∗∣G∣ 替代。
从而有欧拉定理:若 a,m 互素,则 amodm∈⟨m⟩,则 (amodm)∗φ(m)=1,即 (amodb)φ(m)modm=1,从而 aφ(m)≡1(modm)。
即欧拉定理是群论中拉格朗日定理的特殊情形。
循环群
⟨G,∗⟩ 为循环群(cyclic group)当且仅当
∃a∈G,G=⟨a⟩
a 称为 G 的生成元(generator)。
- 有限循环群:若循环群生成元 a 阶为 n,则 G 为有限 n 阶循环群,且 G={a0,a1,⋯,an−1},其中 a0=e
- 无限循环群:若循环群生成元 a 为无限阶元,则 G 为无限循环群,且 G={a0,a±1,⋯},其中 a0=e
若 a 是无限循环群的生成元,则 a−1 也是该无限循环群的生成元。
证明
设群 G=⟨a⟩={ak∣a∈G,k∈Z},则 ak=(a−1)−k,即 G={(a−1)k∣k∈Z},故 G=⟨a−1⟩。
无限循环群有且仅有两个生成元。
证明
设 G=⟨a⟩,若 b 也为 G 生成元,则 ∃m,t∈Z,am=b∧bt=a,故 a=bt=(am)t=amt,消去律有 amt−1=e。
因为 a 为无限阶元,故 mt=1,从而 m=t=1 或 m=t=−1,即 b=a 或 b=a−1。
设有限群 G=⟨a⟩,且 ∣a∣=n,则对任意不大于 n 的正整数 r,有
G=⟨ar⟩⟺gcd(n,r)=1
证明
⟸:设 gcd(n,r)=1,则由裴蜀定理有 ∃u,v∈Z,ur+vn=1,从而
a=aur+vn=auravn=(ar)u
故 G 中任意元素 ak 可表示为 (ar)uk 的形式,即 G=⟨ar⟩。
⟹:设 ar 是 G 生成元,令 gcd(n,r)=d,且 r=dt,则
(an)t=(an)dr=(ar)dn=e
故 ∣ar∣ 整除 dn,但 ∣ar∣=n,故 n∣dn,则 d=1,即 gcd(n,r)=1。
即 n 阶循环群 G 生成元个数为不大于 n 且与 n 互质的正整数个数,即 φ(n)。
令 a 为群 G 的一个 n 阶元素,k 为正整数,有
⟨ak⟩=⟨agcd(n,k)⟩
及
ak=gcd(n,k)n
证明
注意到 gcd(n,k)∣k,则有 ak∈⟨agcd(n,k)⟩。
又有裴蜀定理,∃s,t∈Z,sn+tk=gcd(n,k),则有
agcd(n,k)=asn+tk=asnatk=(ak)t∈⟨ak⟩
同时注意到
(ak)gcd(n,k)n=(an)gcd(n,k)k=e
于是 ak 整除 gcd(n,k)n。
又 ⟨ak⟩=⟨agcd(n,k)⟩,则 ak=agcd(n,k),而 agcd(n,k)⩾gcd(n,k)n(否则若 agcd(n,k)<gcd(n,k)n,则 (agcd(n,k))∣agcd(n,k)∣<∗∣an∣=1,矛盾!),因此 ak=gcd(n,k)n。
推论 1
令 ∣a∣=n,则
- ⟨ai⟩=⟨aj⟩ 当且仅当 gcd(n,i)=gcd(n,j);
- ai=aj 当且仅当 gcd(n,i)=gcd(n,j)。
推论 2
令 ∣a∣=n,则
- ⟨a⟩=⟨ai⟩ 当且仅当 gcd(n,i)=1;
- ∣a∣=ai 当且仅当 gcd(n,i)=1。
设 G=⟨a⟩ 为循环群,证明
- G 的任意子群 H 仍为循环群
- 若 a 为无限阶元,则 G 的非平凡子群 H 均为无限循环群
解答
- 令 ⟨H,∗⟩≤⟨G,∗⟩,从而 H⊆⟨a⟩。
若 H={e},显然成立。
否则取 am 为 H 中最小正方幂元,下证 H=⟨am⟩。
只需证明 H⊆⟨am⟩。任取 h∈H⊆⟨a⟩,故 h=an。
令 n=qm+r,其中 0⩽r<m,从而 h=an=aqm+r=(am)qar,即 ar=h(am)−q,由 m 最小性得 r=0(否则由 0<r<m 有 ar 才是 H 中最小正方幂元),故 h=(am)q,即 h∈⟨am⟩,因此 H 为循环群。
- 设 H≤G,由 1. 知 H=⟨am⟩,若 H={e},则 m=0,从而若 H 有限,则 ∣am∣ 有限,与 a 为无限阶元矛盾,故 H 为无限循环群。
对 n 每个因子 d,n 阶循环群 G 中恰有一个 d 阶子群,且其中该子群的生成元的个数为 φ(d)。
证明
令 H=⟨adn⟩,显然 H 为 G 的 d 阶子群。
若令 H1=⟨am⟩ 也为 d 阶子群,则 (am)d=amd=e,即 n∣md,即 dn∣m,因此 am=(adn)k∈H,即 H1⊆H,又 H1≈H,故 H1=H。
子群为 d 阶循环群,因此该子群的生成元个数为 φ(d)。
因此由这个结论有
n=d∣n∑φ(d)
群的直积
给定两个群 ⟨S,∘⟩,⟨T,∗⟩,定义 S×T 上运算 ⊗ 为
(s1,t1)⊗(s2,t2)=(s1∘s2,t1∗t2)
从而有 ⟨S×T,⊗⟩ 为群,称为群 ⟨S,∘⟩,⟨T,∗⟩ 的直积。
证明
- 结合律:((r1∘s1)∘t1,(r2∗s2)∗t2)=(r1∘s1,r2∗s2)⊗(t1,t2)
- 单位元:(eS,eT)
- 逆元:(s,t)−1=(s−1,t−1)
Ck 表示 k 阶循环群,则 Cm×Cn 为 mn 阶循环群当且仅当 m,n 互质。(即 Cm×Cn≅Cmn⟺gcd(m,n)=1)
证明
⟸:设 gcd(m,n)=1,只需证明 Cm×Cn 中含有阶为 mn 的元素(因为 Cm×Cn 有 mn 个元素,只要证明存在阶为 mn 的元素,就能说明 Cm×Cn 是 mn 阶循环群了)。
设 a,b 分别为 Cm,Cn 的生成元,则 (a,b)mn=e。
若 (a,b)k=e,则 k 为 m,n 公倍数,又 m,n 互质,故 k 为 mn 的倍数,即 (a,b) 为 mn 阶元素。
⟹:若 Cm×Cn 是 mn 阶循环群,则 Cm×Cn 是循环群,生成元为 (s,t),且其阶为 mn。
若 gcd(m,n)=k>1,则 (s,t)kmn=e(因 sm=e1,tn=e2),与 (s,t) 阶是 mn 矛盾(kmn<mn),故 gcd(m,n)=1。
则有若 m,n 互质,则 φ(mn)=φ(m)φ(n)。
置换群
设 S={1,2,⋯,n},S 上的任何双射函数 σ:S→S 称为 S 上的 n 元置换。
σ=[1σ(1)2σ(2)⋯⋯nσ(n)]
置换的乘积定义为置换的复合。
设 σ 是 S={1,2,⋯,n} 上的 n 元置换,若
σ(i1)=i2,σ(i2)=i3,⋯,σ(ik−1)=ik,σ(ik)=i1
且保持 S 中其它元素不变,则称 σ 为 S 上的 k 阶轮换,记作 (i1i2⋯ik)。
若 k=2,则称 σ 为 S 上的对换。
任何 n 元置换可以唯一地表示为不相交的轮换的乘积。
例如
σ=[1523364452617887]
可表示为
σ=(15236)(4)(78)
通常省略 1 阶轮换,即上式可简写为 (15236)(78)。
但对于恒等轮换,得保留 (1),即 (1)(2)⋯(n) 写作 (1)。
轮换可以进一步分解为对换。
设 S={1,2,⋯,n},σ 是 S 上的 k 阶轮换,则 σ 可表示为对换的乘积,且
(i1i2⋯ik)=(i1i2)(i1i3)⋯(i1ik)
但表示方法不唯一。
上面的可以进一步表示为
(15236)(78)=(15)(12)(13)(16)(78)
置换的对换表示不唯一,例如 σ=[12233144] 可表示为 (12)(13) 或 (14)(24)(34)(14)。
但是其奇偶性保持恒定。
若 n 元置换 σ 可表示为奇数个对换之积,则称 σ 为奇置换,否则称 σ 为偶置换。
奇置换和偶置换各有 2n! 个。
n 元集合上所有置换的集合 Sn 关于置换乘法构成群,称为 n 元对称群。
Sn 的任何一个子群称为置换群。
所有 n 元偶置换的集合 An 是 Sn 的一个子群,称为 n 元交错群。
群同构与同构映射
群 ⟨G1,∘⟩,⟨G2,∗⟩ 同构(G1≅G2)当且仅当存在双射函数 f:G1→G2 使得
∀x,y∈G1,f(x∘y)=f(x)∗f(y)
群同构关系是等价关系。
四元循环群
| ∗ |
1 |
2 |
3 |
4 |
| 1 |
1 |
2 |
3 |
4 |
| 2 |
2 |
3 |
4 |
1 |
| 3 |
3 |
4 |
1 |
2 |
| 4 |
4 |
1 |
2 |
3 |
C4≅Z4
Klein 四元群
| ∗ |
1 |
2 |
3 |
4 |
| 1 |
1 |
2 |
3 |
4 |
| 2 |
2 |
1 |
4 |
3 |
| 3 |
3 |
4 |
1 |
2 |
| 4 |
4 |
3 |
2 |
1 |
V4≅Z2×Z2
设 f 是从群 ⟨G,∗⟩ 到群 ⟨H,∘⟩ 的同态映射,则
- f(eG)=eH
- ∀a∈G,f(a−1)=(f(a))−1
1,2,⋯,1000 这 1000 个正整数按任意组合加减,能否得到 1001?
解答
定义系统「奇偶加群」⟨{e,o},∗⟩,运算表为
| ∗ |
e |
o |
| e |
e |
o |
| o |
o |
e |
则 f:Z→{e,o}
{f(x)={e,o,x 为偶数x 为奇数
即 f 是从 ⟨Z,+⟩ 到「奇偶加群」的满同态映射。
blablabla
设 ⟨G,∗⟩ 为无限循环群,则 ⟨G,∗⟩≅⟨Z,+⟩。
证明
设 G 生成元为 a,则 ∣a∣=∞。
令 f:Z→G 为 f(n)=an。
因为
f(m+n)=am+n=am∗an=f(m)f(n)
则 f 为同态映射。
又因为
f(n)=f(m)⟹an=am⟹an−m=e⟹n=m
则 f 为单射。显然 f 还为满射,故 f 为同构映射,即 ⟨G,∗⟩≅⟨Z,+⟩。
设 ⟨G,∗⟩ 为 n 阶循环群,则 ⟨G,∗⟩≅⟨Zn,⊕n⟩(⊕n 表示模 n 加法)。
证明
设 G 生成元为 a,则 ∣a∣=n,G={a0,a1,⋯,an−1}。
令 f:Zn→G 为 f(k)=ak(k=0,1,⋯,n−1)。
因为
f(i⊕nj)=ai⊕nj=ai+j+kn=ai+j=f(i)∗f(j)
故 f 为同态映射。
又因为
f(i)=f(j)⟹ai=aj⟹ai−j=e⟹n∣(i−j)⟹i≡j(modn)⟹i=j
故 f 为单射。显然 f 为满射,故 f 为同构映射,即 ⟨G,∗⟩≅⟨Zn,⊕n⟩。
正规子群
群 G 的子群 H 是 G 的正规子群,当且仅当 ∀a∈G,Ha=aH,记作 H⊴G。
显然平凡子群 ⟨G,∘⟩,⟨{e},∘⟩ 都是正规子群。
Ha=aH 充要条件是
∀hi∈H,a∈G,∃hj∈H,hia=ahj
而非 ∀hi∈H,a∈G,hia=ahi。
群的中心 C 是群 G 的正规子群。即 C⊴G。
中心是什么?
正规子群的判定
设 N 是群 G 的子群,N 是群 G 的正规子群当且仅当
∀g∈G,n∈N,gng−1∈N
证明
必要性:任取 g∈G,n∈N,有 n1∈N 使得 gn=n1g,因此 gng−1=n1∈N。
充分性:先证明 gN⊆Ng。任取 gn∈gN,已知 gng−1∈N,可令 gng−1=n1,则 gn=n1g∈Ng。类似可证明 Ng⊆gN,故 gN=Ng,即 N⊴G。
即设 N 是群 G 的子群,N 是群 G 的正规子群当且仅当
∀g∈G,gNg−1=N
设 N 是群 G 的子群,若 G 的其它子群都不与 N 等势,则 N 是 G 的正规子群。
证明
只需证明 gNg−1=N。
先证明 gNg−1 是个群,从而可得 gNg−1 是 G 的子群:
- 封闭性:(gn1g−1)(gn2g−1)=gng−1
- ab−1:(gn1g−1)(gn2g−1)−1=(gn1g−1)(gn2−1g−1)=gng−1
因为其它子群都不与 N 等势,故只需证明 gNg−1≈N。
注意到消去律,只需证明 gN≈Ng。而这个在上面就已经证明过了,因而得证。
设 N 是群 G 的子群,若 [G:N]=2,则 N 是 G 的正规子群。
证明
[G:N]=2 说明 G 可以划分为两个互不相交的陪集。
为证明 N 是 G 的正规子群,只需证明 ∀g∈G,n∈N,gng−1∈N 即可。
若 g∈N,则显然有 ∀n∈N,gng−1∈N。
若 g∈/N,则 G=N∪gN,且 N∩gN=∅。
考虑 G 的子群 gNg−1,可知有且仅有 gNg−1=N 或 gNg−1=gN。
若 gNg−1=N,则 ∀n∈N,gng−1∈N,得证。
若 gNg−1=gN,则 ∀n∈N,gng−1∈gN,即 ∃n′∈N,gng−1=gn′,从而 ng−1=n′∈N。
或者简单来看,显然有 e∈N,而 geg−1=e∈/gN,故不成立。
故 g−1∈N,得 g∈N,矛盾!因此只能有 gNg−1=N,得证。
设 N⊴G,可以证明若 ap−1,bq−1∈N,则
(ab)(pd)−1∈N
即群 G 中运算可以提升到陪集上,定义
Ha∗Hb=H(ab)
于是正规子群的陪集关系是同余关系。
从而有
若 N⊴G,则 ⟨G/N,∗⟩ 是一个群,称为商群。
证明
- 封闭性:由 ∗ 的定义保证了封闭性
- 结合律:G 运算满足结合律
- 单位元:N(即 Ne)
- 逆元:Na 逆元为 Na−1
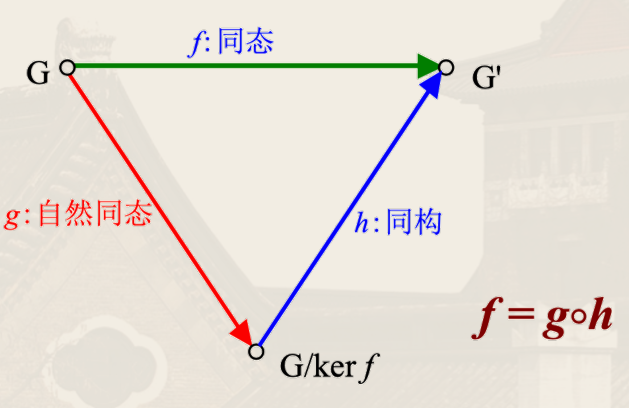
任何群 G 与其商群 G/N 满同态,称为自然同态。
证明
G/N 是由 N 确定的商群,其元素为 N 的陪集。
定义 g:G→G/N,对任意 a∈G,g(a)=Na。
显然 g 是满射,且任意 a,b∈G 有
g(ab)=N(ab)=Na∗Nb=g(a)∗g(b)
即 g 是满同态映射。
同态核
假设群 G1,G2 是群,f:G1→G2 是同态映射,定义集合
kerf={x∣x∈G1∧f(x)=e2}
称为同态核。
同态核是正规子群。即 kerf⊴G1。
证明
- 非空:e1∈kerf
- 子群:任取 a,b∈kerf,则 f(a)=f(b)=e2,则 f(ab−1)=f(a)∗(f(b))−1=e2
- 正规子群:任取 a∈kerf,x∈G1,则 f(a)=e2,因此 f(xax−1)=f(x)∗f(a)∗(f(x))−1=e2,即 gag−1∈kerf。
同态基本定理
设 G,G′ 是群,f:G→G′ 是满同态映射,则 G/kerf≅G′。