降维与度量学习

$k$-近邻学习

$k$ 近邻（$k$-Nearest Neighbor, $k$NN）学习是一种常用的监督学习算法：

• 给定测试样本，基于某种距离度量
• 找出训练集中与其最靠近的 $k$ 个训练样本
  • 在分类任务中使用「投票法」，即选择这 $k$ 个样本中出现最多的类别作为预测结果
  • 在回归任务中使用「平均法」，即选择这 $k$ 个样本的实值输出标记的平均值作为预测结果
  • 还可基于距离远近赋予不同的权重，进行加权投票或加权平均，距离越近的样本权重越大

与之前介绍的学习方法相比，$k$-近邻学习没有显式的训练过程。

按是否在训练阶段就对样本进行学习处理，有两种学习方法：

• 急切学习（eager learning）：在训练阶段就对样本进行学习处理的方法
• 懒惰学习（lazy learning）：在训练阶段仅仅是把样本保存起来，训练时间开销为零，待收到测试样本后再进行处理
  • $k$ 近邻学习是懒惰学习方法的著名代表。

$k$NN 中 $k$ 是一个重要的参数。此外若采用不同的距离计算方式，则找出的近邻可能也有显著的差别，导致分类结果有显著不同。下面是一个示意图：

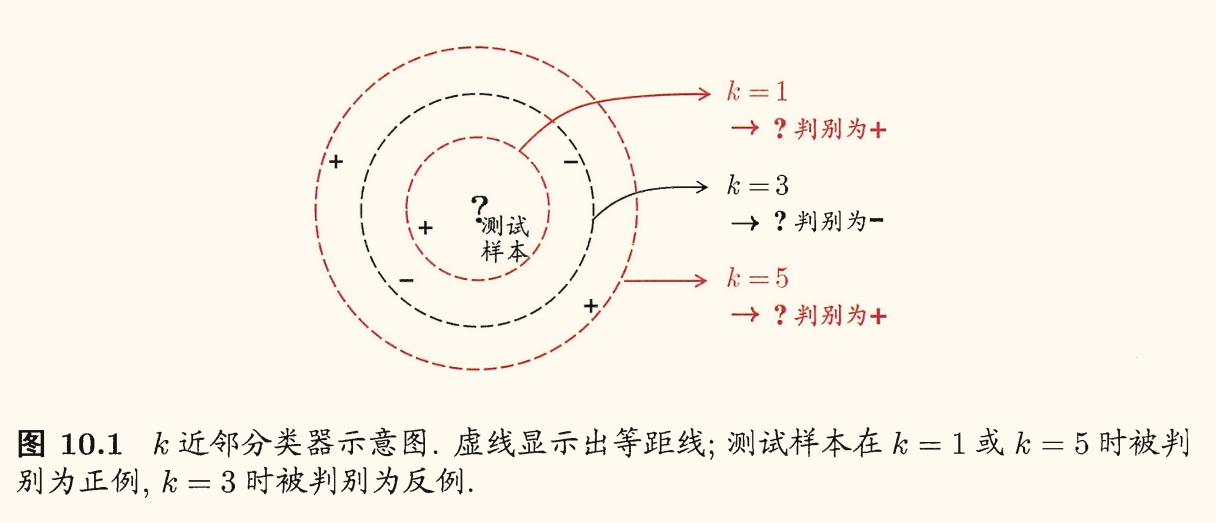
假设距离计算是恰当的，即能够恰当地找出 $k$ 个近邻，下面对「最近邻分类器」，即 $1$NN 在二分类问题上的性能做一个简单的讨论。

给定测试样本 $\bm{x}$，若其最邻近样本为 $\bm{z}$，则最邻近分类器出错的概率就是 $\bm{x}, \bm{z}$ 类别标记不同的概率，即

$$P(\text{err}) = 1 - \sum_{c \in \mathcal{Y}}P(c \mid \bm{x}) P(c \mid \bm{z})$$

假设样本独立同分布，且对任意 $\bm{x}$ 与任意小正数 $\delta$，在 $\bm{x}$ 的 $\delta$-邻域内总能找到一个训练样本。

令 $c^{*} = \argmax\limits_{c \in \mathcal{Y}}P(c \mid \bm{x})$ 为贝叶斯最优分类器的结果，有

$$\begin{aligned} P(\text{err}) &= 1 - \sum_{c \in \mathcal{Y}}P(c \mid \bm{x}) P(c \mid \bm{z}) \\ &\simeq 1 - \sum_{c \in \mathcal{Y}} P^2(c \mid \bm{x}) \\ &\le 1 - P^2(c^{*} \mid \bm{x}) \\ &= (1 + P(c^{*} \mid \bm{x}))(1 - P(c^{*} \mid \bm{x})) \\ &\le 2 \times (1 - P(c^{*} \mid \bm{x})) \\ &= 2P(\text{err}^{*}) \end{aligned}$$

即最近邻分类器虽然很简单，但泛化错误率却不会超过贝叶斯最优分类器的错误率的两倍。

低维嵌入

上面的讨论基于一个重要假设——任意测试样本 $\bm{x}$ 的任意小的 $\delta$-邻域总能找到一个训练样本，即训练样本的采样密度足够大，或称为「密采样」（dense sample）。

但这个假设在现实任务中通常很难满足。例如若 $\delta = 0.001$，对单个维度，需要 $1000$ 个样本点平均分布在归一化后的属性取值范围内，若维数为 $20$，需满足密采样条件，则至少需要 $(10^3)^{20} = 10^{60}$ 个样本。这还仅仅只是维数为 $20$ 的情况，现实应用中属性维数往往更高。

另外当维数很高时，计算内积也不再容易，会给距离计算带来很大的麻烦。

在高维情形下出现的数据样本稀疏、距离计算困难等问题，是所有机器学习方法共同面临的严重障碍，称为「维数灾难」（curse of dimensionality）。

缓解维数灾难的一个重要途径是降维（dimension reduction, 维数约简），即通过某种数学变换，将原始高维属性空间转变为一个低维「子空间」，使得在该子空间中样本密度更高、距离计算更方便。

降维是合理，是因为很多时候观测或收集到的数据样本虽然是高维的，但与学习任务密切相关的也许仅是某个低维分布，即高维空间中的一个低维「嵌入」（embedding），如下图所示：

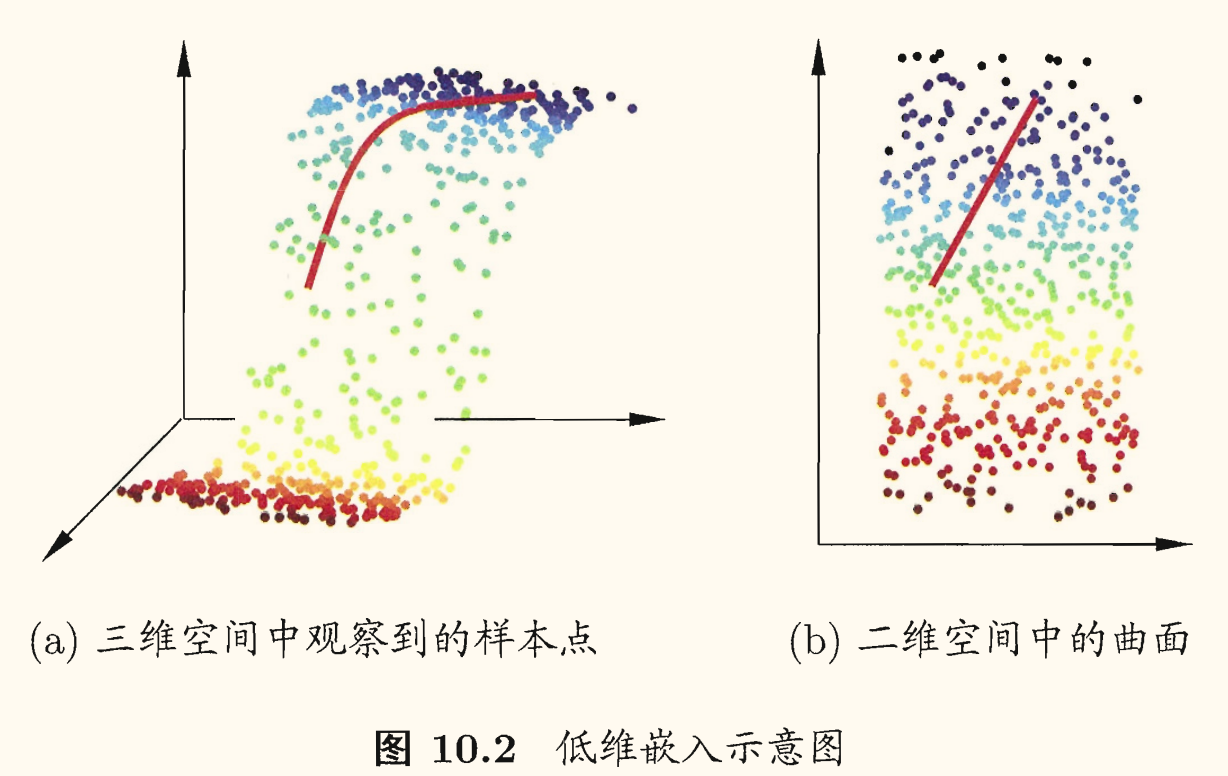
若要求原始空间中样本之间的距离在低维空间中得以保持，如上图所示，则得到「多维缩放」（Multiple Dimensional Scaling, MDS）这一种经典降维方法。

假定 $m$ 个样本在原始空间的距离矩阵为 $\mathbf{D} \in \R^{m \times m}$，其中 $d_{ij} = \operatorname{dist}(\bm{x}_i, \bm{x}_{j})$。

目标是获得样本在 $d'$ 维空间的表示 $\mathbf{Z} \in \R^{d' \times m}$，其中 $d' \le d$，且任意两个样本在 $d'$ 维空间中的欧氏距离等于原始空间中的距离，即

$$\left\lVert \bm{z}_i - \bm{z}_{j} \right\rVert = d_{ij}, \quad \forall i, j$$

令 $\mathbf{B} = \mathbf{Z}^\intercal \mathbf{Z} \in \R^{m \times m}$，其中 $\mathbf{B}$ 为降维后样本的内积矩阵，即 $b_{ij} = \bm{z}_i^\intercal \bm{z}_{j}$。

则有

$$\begin{aligned} d_{ij}^2 &= \left\lVert \bm{z}_i - \bm{z}_{j} \right\rVert^2 \\ &= \left\lVert \bm{z}_i \right\rVert^2 + \left\lVert \bm{z}_{j} \right\rVert^2 - 2\bm{z}_i^\intercal \bm{z}_{j} \\ &= b_{ii} + b_{jj} - 2b_{ij} \end{aligned}$$

为了便于讨论，令降维后的样本 $\mathbf{Z}$ 被中心化，即 $\displaystyle \sum_{i=1}^{m}\bm{z}_i = \bm{0}$，则有 $\mathbf{B}$ 行与列之和均为零，即 $\displaystyle \sum_{i=1}^{m}b_{ij} = \sum_{j=1}^{m}b_{ij} = 0$。

由此可得

$$\left\lbrace\begin{aligned} \sum_{i=1}^{m}d_{ij}^2 &= \trace(\mathbf{B}) + m \cdot b_{jj} \\ \sum_{j=1}^{m}d_{ij}^2 &= \trace(\mathbf{B}) + m \cdot b_{ii}\\ \sum_{i=1}^{m}\sum_{j=1}^{m}d_{ij}^2 &= 2m \cdot \trace(\mathbf{B}) \end{aligned}\right.$$

其中有 $\trace(\mathbf{B}) = \displaystyle \sum_{i=1}^{m}\left\lVert \bm{z}_i \right\rVert^2$。

令

$$\begin{equation} \left\lbrace\begin{aligned} d_{i \odot}^2 &= \frac{1}{m}\sum_{j=1}^{m}d_{ij}^2 \\ d_{\odot j}^2 &= \frac{1}{m}\sum_{i=1}^{m}d_{ij}^2 \\ d_{\odot \odot}^2 &= \frac{1}{m^2}\sum_{i=1}^{m}\sum_{j=1}^{m}d_{ij}^2 \end{aligned}\right. \label{1} \end{equation}$$

则有

$$\begin{equation} b_{ij} = -\dfrac{1}{2}(d_{ij}^2 - d_{i \odot}^2 - d_{\odot j}^2 + d_{\odot \odot}^2) \label{2} \end{equation}$$

也就是说，可以通过降维前后保持不变的距离矩阵 $\mathbf{D}$ 求取内积矩阵 $\mathbf{B}$。

对内积矩阵 $\mathbf{B}$ 进行特征值分解，有 $\gdef\diag{\operatorname{diag}}\mathbf{B} = \mathbf{V} \mathbf{\Lambda} \mathbf{V}^\intercal$，其中 $\mathbf{\Gamma} = \diag(\lambda_1, \dots, \lambda_{d})$ 为特征值构成的对角矩阵，且 $\lambda_1 \ge \dots \ge \lambda_d$。

$\mathbf{V}$ 为特征向量矩阵，假定其中有 $d^{*}$ 个非零特征值，构成对角矩阵 $\mathbf{\Lambda}_{*} = \diag(\lambda_1, \dots, \lambda_{d^{*}})$，令 $\mathbf{V}_{*}$ 表示相应的特征向量矩阵，则 $\mathbf{Z}$ 可表达为

$$\mathbf{Z} = \mathbf{\Lambda}_{*}^{1 / 2}\mathbf{V}_{*}^\intercal \in \R^{d^{*} \times m}$$

现实应用中为了有效降维，往往仅需降维后的距离与原始空间中的距离尽可能接近，而不必严格相等。此时可取 $d' \ll d$ 个最大特征值构成对角矩阵 $\tilde{\mathbf{\Lambda}} = \diag(\lambda_1, \dots, \lambda_{d'})$，对应的特征向量矩阵 $\tilde{\mathbf{V}}$，则降维后的样本表示为

$$\tilde{\mathbf{Z}} = \tilde{\mathbf{\Lambda}}^{1 / 2}\tilde{\mathbf{V}}^\intercal \in \R^{d' \times m}$$

下面是 MDS 算法的描述：

1. 按 $\eqref{1}$ 计算 $d_{i \odot }^2, d_{\odot j}^2, d_{\odot \odot}^2$；
2. 按 $\eqref{2}$ 计算 $\mathbf{B}$
3. 对 $\mathbf{B}$ 进行特征值分解；
4. 取 $\tilde{\mathbf{\Lambda}}$ 为 $d'$ 个最大特征值构成的对角矩阵，$\tilde{\mathbf{V}}$ 为相应的特征向量矩阵；
5. 输出：$\tilde{\mathbf{\Lambda}}^{1 / 2}\tilde{\mathbf{V}}^\intercal \in \R^{m \times d'}$，每行是一个样本的低维坐标。

一般来说，欲获得低维子空间，最简单的是对原始高维空间进行线性变换。给定 $d$ 维空间中的样本 $\mathbf{X} = (\bm{x}_1 \dots, \bm{x}_m) \in \R^{d \times m}$，变换之后得到 $d' \le d$ 维空间中的样本

$$\mathbf{Z} = \mathbf{W}^\intercal \mathbf{X}$$

其中 $\mathbf{W} \in \R^{d \times d'}$ 是变换矩阵，$\mathbf{Z} \in \R^{d' \times m}$ 是样本在新空间中的表述。

变换矩阵可视为 $d'$ 个 $d$ 维向量，$\bm{z}_i = \mathbf{W} \bm{x}_i$ 是第 $i$ 个样本与这 $d'$ 个基向量分别做内积而得到的 $d'$ 维属性向量。

换言之，$\bm{z}_i$ 是原属性向量 $\bm{x}_i$ 在新坐标系 $\left\lbrace \bm{w}_1, \dots, \bm{w}_{d'} \right\rbrace$ 中的坐标向量。

若 $\bm{w}_i, \bm{w}_{j}$ 正交，则新坐标系是一个正交坐标系，此时 $\mathbf{W}$ 为正交变换。

显然新空间中的属性是原空间中属性的线性组合。

基于线性变换来进行降维的方法称为「线性降维方法」，都符合 $\mathbf{Z} = \mathbf{W}^\intercal \mathbf{X}$ 的基本形式，不同之处在于对低维子空间的性质有不同要求，相当于对 $\mathbf{W}$ 施加了不同的约束。

对降维效果的评估，通常是比较降维前后学习器的性能，若性能有所提高则认为降维起到了作用。若将维数降至二维或三维，则可通过可视化技术来直观地判断降维效果。

主成分分析

主成分分析（Principal Component Analysis, PCA）是最常用的一种降维方法。

对于正交属性空间中的样本点，如何用一个超平面对所有样本进行恰当的表达？

• 最近重构性：样本点到这个超平面的距离都足够近
• 最大可分性：样本点在这个超平面上的投影尽可能分开

基于这两个性质，能分别得到 PCA 的两种等价推导。

最近重构性

假设数据样本进行了中心化，即 $\displaystyle \sum_{i}\bm{x}_i = \bm{0}$，再假定投影变换后得到的新坐标系为 $\left\lbrace \bm{w}_1, \dots, \bm{w}_d \right\rbrace$，其中 $\bm{w}_i$ 是标准正交基向量（$\left\lVert \bm{w}_i \right\rVert_2 = 1,\, \bm{w}_i^\intercal \bm{w}_{j} = 0$）。

若丢弃新坐标系中的部分坐标，即将维度降低到 $d' < d$，则样本点 $\bm{x}_i$ 在低维坐标系中的投影为 $\bm{z}_i = (z_{i 1}; \dots; z_{id'})$，其中 $z_{ij} = \bm{w}_j^\intercal \bm{x}_i$ 是 $\bm{x}_i$ 在低维坐标系下第 $j$ 维的坐标。若基于 $\bm{z}_i$ 来重构 $\bm{x}_i$，则会得到 $\hat{\bm{x}}_i = \displaystyle \sum_{j=1}^{d'} z_{ij}\bm{w}_{j}$。

考虑整个训练集，原样本点 $\bm{x}_i$ 与基于投影重构的样本点 $\hat{\bm{x}}_i$ 之间的距离为

$$\begin{aligned} \sum_{i=1}^{m} \left\lVert \sum_{j=1}^{d'}z_{ij}\bm{w}_{j} - \bm{x}_i \right\rVert_2^2 &= \sum_{i=1}^{m} \left( \sum_{j=1}^{d'}z_{ij}\bm{w}_{j} - \bm{x}_i \right)^\intercal \left( \sum_{j=1}^{d'}z_{ij}\bm{w}_{j} - \bm{x}_i \right) \\ &= \sum_{i=1}^{m} \left( \sum_{j=1}^{d'}z_{ij}\bm{w}_{j} \right)^\intercal \left( \sum_{j=1}^{d'}z_{ij}\bm{w}_{j} \right) - 2 \sum_{i=1}^{m} \left( \sum_{j=1}^{d'}z_{ij}\bm{w}_{j} \right)^\intercal \bm{x}_i + \sum_{i=1}^{m} \bm{x}_i^\intercal \bm{x}_i\\ &= \sum_{i=1}^{m} \sum_{j=1}^{d'} z_{ij}^2 - 2 \sum_{i=1}^{m} \sum_{j=1}^{d'} z_{ij}\bm{w}_{j}^\intercal \bm{x}_i + \sum_{i=1}^{m} \bm{x}_i^\intercal \bm{x}_i\\ &= \sum_{i=1}^{m} \bm{z}_i^\intercal \bm{z}_i - 2 \sum_{i=1}^{m}\bm{z}_i^\intercal \mathbf{W}^\intercal \bm{x}_i + \text{constant}\\ &\propto - \trace \left( \mathbf{W}^\intercal \left( \sum_{i=1}^{m}\bm{x}_i \bm{x}_i^\intercal \right) \mathbf{W} \right) \end{aligned}$$

根据最近重构性，上式应被最小化。考虑到 $\bm{w}_{j}$ 是标准正交基，且 $\displaystyle \sum_i \bm{x}_i \bm{x}_i^\intercal$ 是协方差矩阵，有主成分分析的优化目标

$$\begin{equation} \min_{\mathbf{W}} - \trace \left( \mathbf{W}^\intercal \mathbf{X} \mathbf{X}^\intercal \mathbf{W} \right) \quad \text{s.t.} \quad \mathbf{W}^\intercal \mathbf{W} = \mathbf{I} \label{3} \end{equation}$$

其中 $\mathbf{X} = (\bm{x}_1, \dots, \bm{x}_m) \in \R^{d \times m}$，$\mathbf{W} = (\bm{w}_1, \dots, \bm{w}_{d'}) \in \R^{d \times d'}$。

最大可分性

样本点 $\bm{x}_i$ 在新空间中超平面上的投影为 $\mathbf{W}^\intercal \bm{x}_i$。若所有样本点的投影能尽可能分开，则应该使投影后样本点的方差最大化。

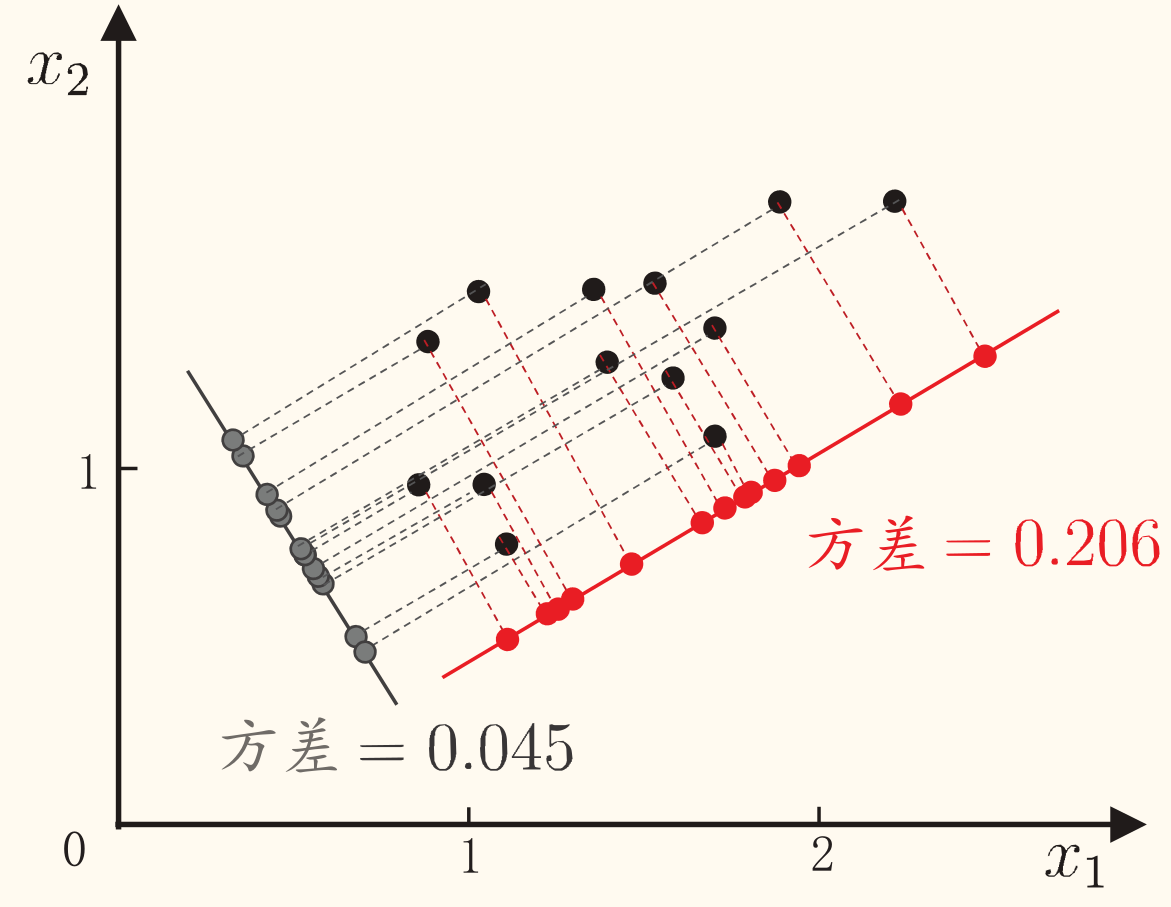
投影后样本点的方差为 $\displaystyle \sum_i \mathbf{W}^\intercal \bm{x}_i \bm{x}_i^\intercal \mathbf{W}$，于是优化目标可写为

$$\begin{equation} \max_{\mathbf{W}} \trace \left( \mathbf{W}^\intercal \mathbf{X} \mathbf{X}^\intercal \mathbf{W} \right) \quad \text{s.t.} \quad \mathbf{W}^\intercal \mathbf{W} = \mathbf{I} \label{4} \end{equation}$$

这与 $\eqref{3}$ 是等价的。

求解

使用拉格朗日乘子法可得

$$\mathbf{X} \mathbf{X}^\intercal \mathbf{W} = \lambda \mathbf{W}$$

于是只需对协方差矩阵 $\mathbf{X} \mathbf{X}^\intercal$ 进行特征值分解^[1]，将求得特征值进行排序 $\lambda_1 \ge \dots \ge \lambda_d$，再取前 $d'$ 个特征值对应的特征向量构成 $\mathbf{W} = (\bm{w}_1, \dots, \bm{w}_{d'})$，这就是主成分分析的解。

PCA 算法描述如下：

1. 对所有样本进行中心化：$\bm{x}_i \gets \bm{x}_i - \displaystyle \frac{1}{m}\sum_{i=1}^{m}\bm{x}_i$；
2. 计算样本的协方差矩阵 $\mathbf{X} \mathbf{X}^\intercal$；
3. 对协方差矩阵进行特征值分解；
4. 取前 $d'$ 个最大特征值对应的特征向量 $\bm{w}_1, \dots, \bm{w}_{d'}$；
5. 输出：投影矩阵 $\mathbf{W}^{*} = (\bm{w}_1, \dots, \bm{w}_{d'})$。

降维后低维空间的维数 $d'$ 通常是由用户事先指定，或通过在 $d'$ 值不同的低维空间中对 $k$ 近邻分类器（或其他开销较小的学习器）进行交叉验证，来选取较好的 $d'$ 值。

对 PCA，还可从重构的角度设置一个重构阈值 $t$（例如 $95\%$），然后选取使下式成立的最小 $d'$ 值：

$$\frac{\sum_{i=1}^{d'}\lambda_i}{\sum_{i=1}^{d}\lambda_i} \ge t$$

PCA 仅需保留 $\mathbf{W}^{*}$ 与样本的均值向量（均值向量是为了中心化），即可通过简单的向量减法与矩阵-向量乘法，将新样本投影至低维空间中。

低维空间与原始高维空间必有不同，因为对应的最小的 $d - d'$ 个特征值的特征向量被舍弃了，这也是降维导致的结果。但舍弃这部分信息往往是必要的：一方面，舍弃这部分信息之后能使样本的采样密度增大，这正是降维的重要动机；另一方面，当数据受到噪声影响时，最小的特征值所对应的特征向量往往与噪声有关，将它们舍弃能在一定程度上起到去噪的效果。

核化线性降维

线性降维方法假设从高维空间到低维空间的函数映射是线性的，然而，在不少现实任务中，可能需要非线性映射才能找到恰当的低维嵌：

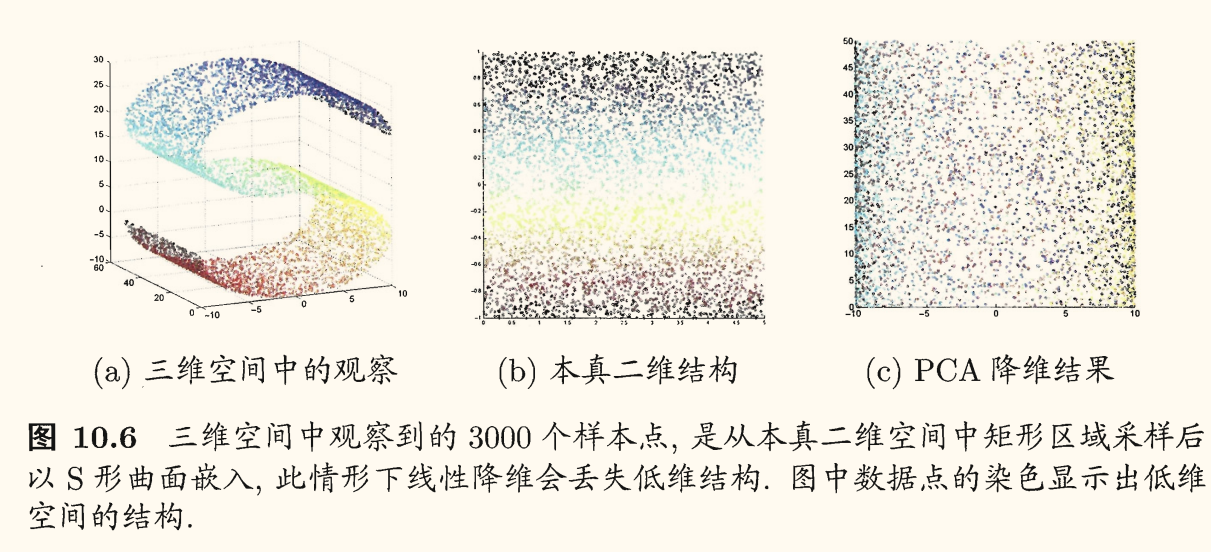
其中将「原本采样」的低维空间称为「本真」（intrinsic）低维空间，以区别于降维后的低维空间。

非线性降维的一种常用方法，就是基于核技巧对线性降维方法进行「核化」。下面是核主成分分析（Kernelized PCA, KPCA）的描述。

假定我们将在高维特征空间中把数据投影到由 $\mathbf{W} = (\bm{w}_1, \dots, \bm{w}_d)$ 确定的超平面上，则对于 $\bm{w}_{j}$ 有

$$\left( \sum_{i=1}^{m}\bm{z}_i \bm{z}_i^\intercal \right) \bm{w}_{j} = \lambda_j \bm{w}_{j}$$

其中 $\bm{z}_i$ 是样本点 $\bm{x}_i$ 在高维特征空间中的像。

令 $\bm{\alpha}_i^{j} = \dfrac{1}{\lambda_{j}} \bm{z}_i^\intercal \mathbf{W}$，有

$$\begin{aligned} \bm{w}_{j} &= \dfrac{1}{\lambda_{j}} \left( \sum_{i=1}^{m} \bm{z}_i \bm{z}_i^\intercal \right) \bm{w}_{j}\\ &= \sum_{i=1}^{m} \bm{z}_i \dfrac{\bm{z}_i^\intercal \bm{w}_{j}}{\lambda_{j}}\\ &= \sum_{i=1}^{m} \bm{z}_i \alpha_i^{j} \end{aligned}$$

假定 $\bm{z}_i$ 是由原始属性空间中的样本点 $\bm{x}_i$ 通过映射 $\phi$ 产生的，即

$$\bm{z}_i = \phi(\bm{x}_i)\quad ,\,i=1, 2, \dots, m.$$

若 $\phi$ 能被显式表达出来，则通过它将样本映射至高维空间，再在特征空间中实施 PCA 即可，即有

$$\left( \sum_{i=1}^{m} \phi(\bm{x}_i) \phi(\bm{x}_i)^\intercal \right) \bm{w}_{j} = \lambda_{j} \bm{w}_{j}$$

与

$$\bm{w}_{j} = \sum_{i=1}^{m} \phi(\bm{x}_i) \alpha_i^{j}$$

对于 $\mathbf{W}$ 即为 $\mathbf{W} = \displaystyle \sum_{i=1}^{m} \bm{z}_i \bm{\alpha}_i$。

一般情形下不清楚 $\phi$ 的具体形式，因此引入核函数

$$\kappa(\bm{x}_i, \bm{x}_{j}) = \phi(\bm{x}_i)^\intercal \phi(\bm{x}_{j})$$

又由 $\bm{w}_{j}$ 的值，代入优化式可得

$$\mathbf{K} \bm{\alpha}^{j} = \lambda_{j} \bm{\alpha}^{j}$$

其中 $\mathbf{K}$ 为 $\kappa$ 对应的核矩阵，有 $(\mathbf{K})_{ij} = \kappa(\bm{x}_i, \bm{x}_{j})$ 与 $\bm{\alpha}^{j} = (\alpha_1^{j}; \dots; \alpha_m^{j})$。

上式为特征值分解问题，取 $\mathbf{K}$ 最大的 $d'$ 个特征值对应的特征向量即可。

对新样本 $\bm{x}$，其投影后第 $j$ 维坐标为

$$\begin{aligned} z_{j} &= \bm{w}_{j}^\intercal \phi(\bm{x}) \\ &= \sum_{i=1}^{m} \alpha_i^{j} \phi(\bm{x}_i)^\intercal \phi(\bm{x})\\ &= \sum_{i=1}^{m} \alpha_i^{j} \kappa(\bm{x}_i, \bm{x}) \end{aligned}$$

其中 $\bm{\alpha}_i$ 已经过规范化。

可见，为获得投影后的坐标，KPCA 需对所有样本求和，因此它的计算开销较大。

上述推导的书上版本

书上的推导直接使用了 $\mathbf{W}$。假定我们将在高维特征空间中把数据投影到由 $\mathbf{W}$ 确定的超平面上，即 PCA 欲求解

$$\left( \sum_{i=1}^{m} \bm{z}_i \bm{z}_i^\intercal \right) \mathbf{W} = \lambda \mathbf{W}$$

其中 $\bm{z}_i$ 是样本点 $\bm{x}_i$ 在高维特征空间中的像。

令 $\bm{\alpha}_i = \dfrac{1}{\lambda} \bm{z}_i^\intercal \mathbf{W}$，有

$$\begin{aligned} \mathbf{W} = \dfrac{1}{\lambda} \left( \sum_{i=1}^{m}\bm{z}_i \bm{z}_i^\intercal \right) \mathbf{W}\\ &= \sum_{i=1}^{m} \bm{z}_i \dfrac{\bm{z}_i^\intercal \mathbf{W}}{\lambda}\\ &= \sum_{i=1}^{m} \bm{z}_i \bm{\alpha}_i \end{aligned}$$

$\bm{z}_i = \phi(\bm{x}_i)$ 可得 PCA 欲求解的式子进一步有

$$\left( \sum_{i=1}^{m} \phi(\bm{x}_i) \phi(\bm{x}_i)^\intercal \right) \mathbf{W} = \lambda \mathbf{W}$$

与

$$\mathbf{W} = \sum_{i=1}^{m} \phi(\bm{x}_i) \bm{\alpha}_i$$

引入核函数后代入化简欲求解的式子为

$$\mathbf{K} \mathbf{A} = \lambda \mathbf{A}$$

其中 $\mathbf{K}$ 为核矩阵，$\mathbf{A} = (\bm{\alpha}_i; \dots; \bm{\alpha}_m)$。

上式为特征值分解问题，取 $\mathbf{K}$ 最大的 $d'$ 个特征值对应的特征向量即可。

对新样本 $\bm{x}$ 有

$$\begin{aligned} \bm{z} &= \mathbf{W}^\intercal \phi(\bm{x})\\ &= \sum_{i=1}^{m} \bm{\alpha}_i \phi(\bm{x}_i)^\intercal \phi(\bm{x})\\ &= \sum_{i=1}^{m} \bm{\alpha}_i \kappa(\bm{x}_i, \bm{x}) \end{aligned}$$

其中 $\bm{\alpha}_i$ 已经过规范化。

流形学习

流形学习（manifold learning）是一类借鉴了拓扑流形概念的降维方法。「流形」是在局部与欧氏空间同胚的空间，换言之，它在局部具有欧氏空间的性质，能用欧氏距离来进行距离计算。

若低维流形嵌入到高维空间中，则数据样本在高维空间的分布虽然看上去非常复杂，但在局部上仍具有欧氏空间的性质，因此，可以容易地在局部建立降维映射关系，然后再设法将局部映射关系推广到全局。

当维数被降至二维或三维时，能对数据进行可视化展示，因此流形学习也可被用于可视化。

等度量映射

等度量映射（Isometric Mapping, Isomap）的基本出发点，是认为低维流形嵌入到高维空间之后，直接在高维空间中计算直线距离具有误导性，因为高维空间中的直线距离在低维嵌入流形上不可达。

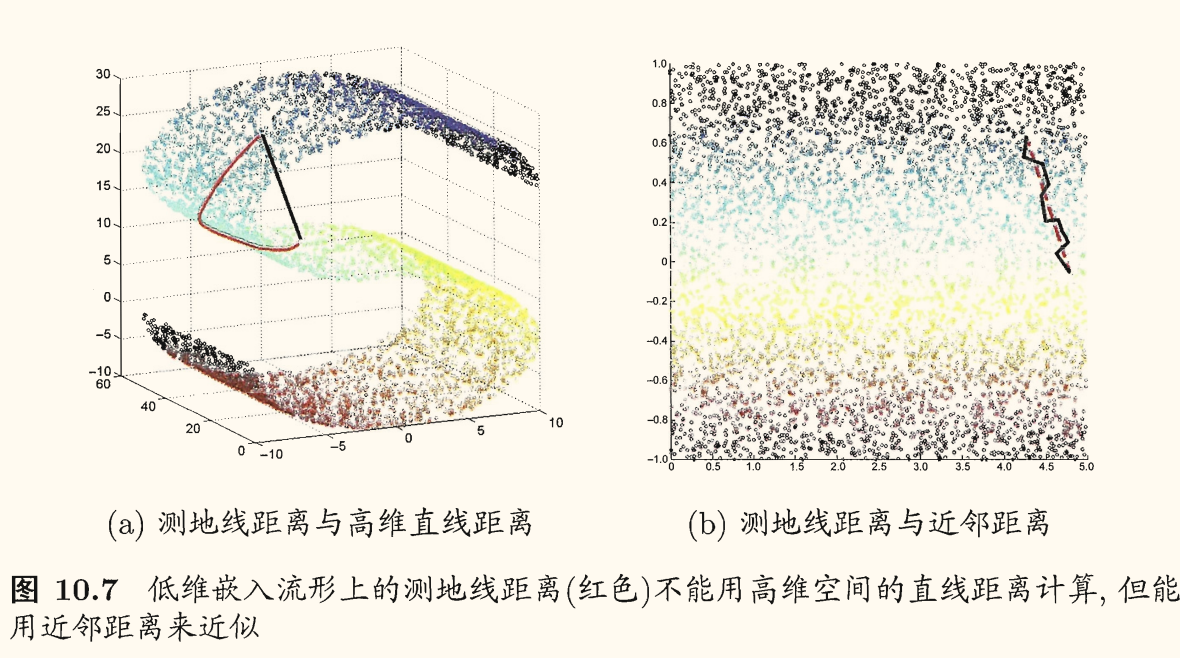
低维嵌入流形上两点间的本真距离是「测地线」（geodesic） 距离。

测地线距离的计算：利用流形在局部上与欧氏空间同胚这个性质，对每个点基于欧氏距离找出其近邻点，然后就能建立一个近邻连接图，图种近邻点之间存在连接，而非近邻点之间不存在连接，于是，计算两点之间测地线距离的问题，就转变为计算近邻连接图上两点之间的最短路径问题。

最短路径的计算可通过 Dijkstra 算法或 Floyd 算法来实现。得到距离后可通过多维缩放方法（MDS）获得样本点在低维空间中的坐标。

Isomap 算法描述如下：

Isomap 仅是得到了训练样本在低维空间的坐标，但对于新样本，如何将其映射到低维空间呢？

这个问题的常用解决方案，是将训练样本的高维空间坐标作为输入，低维空间坐标作为输出，训练一个回归学习器对新样本的低维空间坐标进行预测。

这仅是一个权宜之计，目前似乎没有更好的办法。

对近邻图的构建通常有两种做法：

1. 指定近邻点个数：如欧式距离最近的 $k$ 个点为近邻点，这样得到的近邻图称为 $k$ 近邻图；
2. 指定距离阈值：距离小于阈值 $\epsilon$ 的点被认为是近邻点，这样得到的近邻图称为 $\epsilon$ 近邻图。

不足：

• 若近邻范围指定得较大，则距离很远的点可能被误认为近邻，这样就出现「短路」问题；
• 若近邻范围指定得较小，则近邻图可能不连通，这样就出现「断路」问题。

局部线性嵌入

局部线性嵌入（Locally Linear Embedding, LLE）试图保持邻域内样本之间的线性关系。

假定样本点 $\bm{x}_i$ 能通过它的邻域样本 $\bm{x}_{j}, \bm{x}_{k}, \bm{x}_l$ 的坐标通过线性组合 $\bm{x}_i = w_{ij}\bm{x}_{j} + w_{ik}\bm{x}_{k} + w_{il}\bm{x}_{l}$ 而重构出来，LLE 希望这样的关系在低维空间中得以保持，如下图所示：

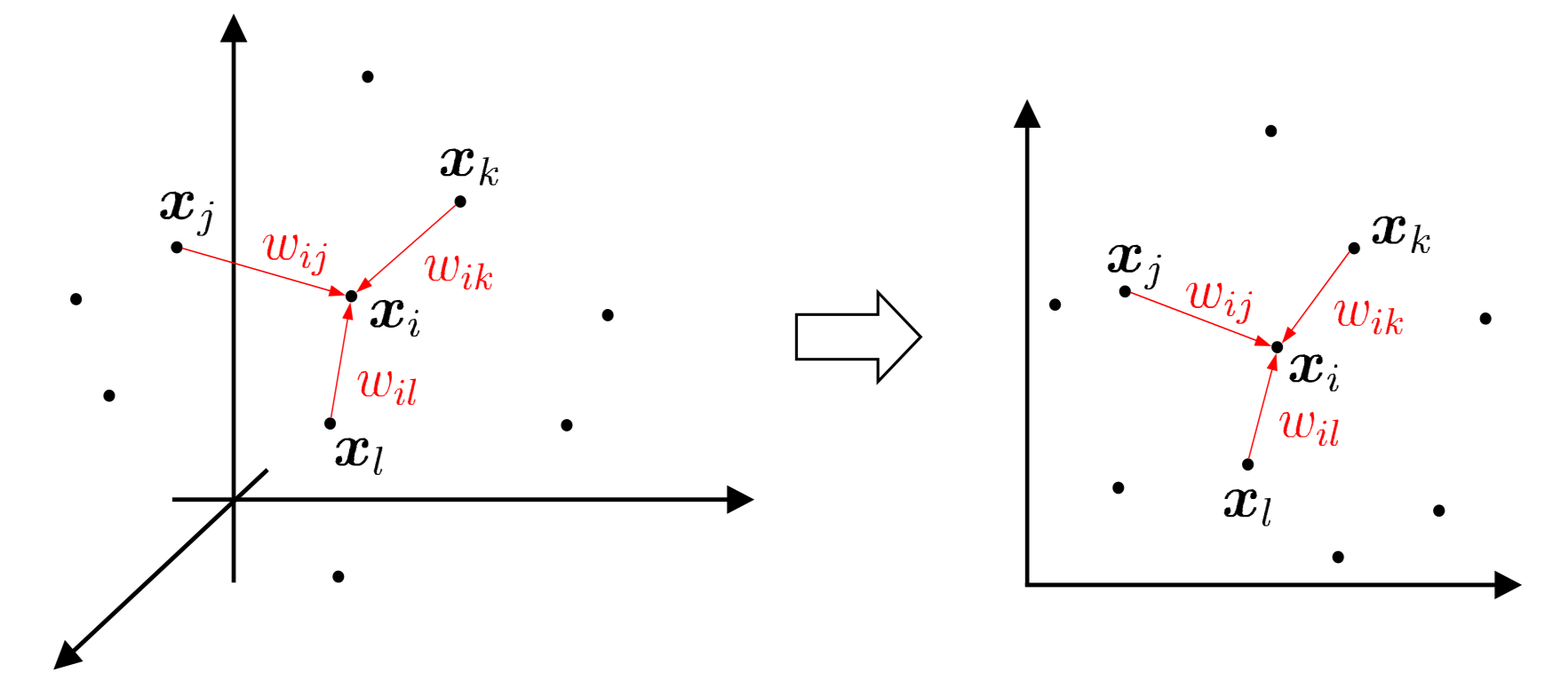
LLE 先为每个样本 $\bm{x}_i$ 找到其近邻下标集合 $Q_i$，然后计算出基于 $Q_i$ 中的样本点对 $\bm{x}_i$ 进行线性重构的系数 $\bm{w}_i$：

$$\min_{\bm{w}_1, \dots, \bm{w}_m} \sum_{i=1}^{m} \left\lVert \bm{x}_i - \sum_{j \in Q_i}w_{ij}\bm{x}_j \right\rVert_2^2\quad \text{s.t.} \quad \sum_{j \in Q_i}w_{ij} = 1$$

其中 $\bm{x}_i, \bm{x}_{j}$ 已知，令 $C_{jk} = (\bm{x}_i - \bm{x}_j)^\intercal(\bm{x}_i - \bm{x}_{k})$，则 $w_{ij}$ 有闭式解

$$w_{ij} = \dfrac{\sum_{k \in Q_i}C_{jk}^{-1}}{\sum_{l, s \in Q_i}C_{ls}^{-1}}$$

LLE 在低维空间中保持 $\bm{w}_i$ 不变，于是 $\bm{x}_i$ 对应的低维空间坐标 $\bm{z}_i$ 可通过下式求解：

$$\min_{\bm{z}_1, \dots, \bm{z}_m} \sum_{i=1}^{m} \left\lVert \bm{z}_i - \sum_{j \in Q_i}w_{ij}\bm{z}_j \right\rVert_2^2$$

这与上面的优化目标同形，区别是优化目标需确定的是 $\bm{w}_i$，而这里则是 $\bm{x}_i$ 对应的低维空间坐标 $\bm{z}_i$。

令 $\mathbf{Z} = (\bm{z}_1, \dots, \bm{z}_m) \in \R^{d' \times m},\, \mathbf{W} = (w_{ij}) \in \R^{m \times m}$，则有

$$\mathbf{M} = (\mathbf{I} - \mathbf{W})^\intercal(\mathbf{I} - \mathbf{W})$$

可将求解式子重写为

$$\min_{\mathbf{Z}} \trace(\mathbf{Z} \mathbf{M} \mathbf{Z}^\intercal)\quad \text{s.t.} \quad \mathbf{Z}\mathbf{Z}^\intercal = \mathbf{I}$$

上式可通过特征值分解求解：$\mathbf{M}$ 最小的 $d'$ 个特征值对应的特征向量组成的矩阵即为 $\mathbf{Z}^\intercal$。

LLE 算法描述如下：

算法第 4 行显示出，对于不在样本 $\bm{x}_i$ 邻域区域的样本 $\bm{x}_{j}$，无论其如何变化都对 $\bm{x}_i, \bm{z}_i$ 没有任何影响，即「将变动限制在局部」的思想。

度量学习

在机器学习中，对高维数据进行降维的主要目的是希望找到一个合适的低维空间，在此空间中进行学习能比原始空间性能更好。事实上，每个空间对应了在样本属性上定义的一个距离度量，而寻找合适的空间，实质上就是在寻找一个合适的距离度量。那么，为何不直接尝试「学习」出一个合适的距离度量呢？

欲对距离度量进行学习，必须有一个便于学习的距离度量表达形式。

对两个 $d$ 维样本 $\bm{x}_i, \bm{x}_{j}$，它们之间的平方欧氏距离可写为

$$\operatorname{dist}_{\text{ed}}^2(\bm{x}_i, \bm{x}_{j}) = \left\lVert \bm{x}_i - \bm{x}_{j} \right\rVert_2^2 = d_{ij, 1}^2 + \dots + d_{ij, d}^2$$

其中 $d_{ij, k} = \left\lVert \bm{x}_{ik} - \bm{x}_{jk} \right\rVert_2$ 是 $\bm{x}_i, \bm{x}_{j}$ 在第 $k$ 维上的距离。

假定不同属性的重要性不同，则可引入属性权重 $\bm{w}$ 得到

$$\begin{aligned} \operatorname{dist}_{\text{wed}}^2(\bm{x}_i, \bm{x}_{j}) &= w_1 \cdot d_{ij, 1}^2 + \dots + w_d \cdot d_{ij, d}^2\\ &= (\bm{x}_i - \bm{x}_{j})^\intercal \mathbf{W} (\bm{x}_i - \bm{x}_{j}) \end{aligned}$$

其中 $w_i \ge 0$，$\mathbf{W} = \operatorname{diag}(\bm{w})$ 是一个对角矩阵，$(\mathbf{W})_{ii} = w_i$，可通过学习确定。

由于 $\mathbf{W}$ 非对角元素均为零，这意味着坐标轴是正交的，即属性之间无关。但现实问题往往不是这样的。

为此，将 $\mathbf{W}$ 替换为一个普通的半正定对称矩阵 $\mathbf{M}$，就得到了马氏距离（Mahalanobis distance）：

$$\begin{aligned} \operatorname{dist}_{\text{mah}}^2(\bm{x}_i, \bm{x}_{j}) &= (\bm{x}_i - \bm{x}_{j})^\intercal \mathbf{M} (\bm{x}_i - \bm{x}_{j})\\ &= \left\lVert \bm{x}_i - \bm{x}_{j} \right\rVert_{\mathbf{M}}^2 \end{aligned}$$

其中 $\mathbf{M}$ 亦称为「度量矩阵」。

度量学习则是对 $\mathbf{M}$ 进行学习。

为了保持距离非负且对称，$\mathbf{M}$ 必须是半正定对称矩阵，即必有正交基 $\mathbf{P}$ 使得 $\mathbf{M} = \mathbf{P} \mathbf{P}^\intercal$，这部分可参见《线性代数》的笔记「实二次型」。

对 $\mathbf{M}$ 的学习要设置一个目标，假定我们是希望提高近邻分类器的性能，则可将 $\mathbf{M}$ 直接嵌入到近邻分类器的评价指标中去，通过优化该性能指标相应地求得 $\mathbf{M}$。

下面以「近邻成分分析」为例进行讨论。

近邻成分分析

近邻成分分析（Neighbourhood Component Analysis, NCA）在进行判别时通常使用多数投票法，邻域中的每个样本投 1 票，邻域外的样本投 0 票。不妨将其替换为概率投票法。

对于任意样本 $\bm{x}_{j}$，它对 $\bm{x}_i$ 分类结果影响的概率为

$$p_{ij} = \dfrac{\exp\left( -\left\lVert \bm{x}_i - \bm{x}_{j} \right\rVert_{\mathbf{M}}^2 \right) }{\sum_l \exp\left( -\left\lVert \bm{x}_i - \bm{x}_{l} \right\rVert_{\mathbf{M}}^2 \right)}$$

当 $i = j$ 时有 $P_{ij}$ 最大。$\bm{x}_{j}$ 对 $\bm{x}_i$ 的影响随着它们之间的距离增大而减小，这是符合直觉的。

若以留一法（LOO）正确率的最大化为目标，则可计算 $\bm{x}_i$ 的留一法正确率，即它被自身以外的所有样本正确分类的概率为

$$p_i = \sum_{j \in \Omega_i} p_{ij}$$

其中 $\Omega_i$ 表示与 $\bm{x}_i$ 属于相同类别的样本的下标集合。

于是整个样本集上留一法正确率为

$$\sum_{i=1}^{m}p_i = \sum_{i=1}^{m}\sum_{j \in \Omega_i} p_{ij}$$

考虑 $p_{ij}$ 的表达式，以及 $\mathbf{M} = \mathbf{P} \mathbf{P}^\intercal$，NCA 的优化目标为

$$\min_{\mathbf{P}} 1 - \sum_{i=1}^{m}\sum_{j \in \Omega_i} \dfrac{\exp\left( -\left\lVert \mathbf{P}^\intercal \bm{x}_i - \mathbf{P}^\intercal \bm{x}_{j} \right\rVert_2^2 \right) }{\sum_l \exp\left( -\left\lVert \mathbf{P}^\intercal \bm{x}_i - \mathbf{P}^\intercal \bm{x}_{l} \right\rVert_2^2 \right)}$$

求解上式即可得到最大化近邻分类器 LLO 正确率的距离度量矩阵 $\mathbf{M}$。

领域知识

实际上，我们不仅能把错误率这样的监督学习目标作为度量学习的优化目标，还能在度量学习中引入领域知识。

若已知某些样本相似、某些样本不相似，则可定义「必连」（must-link）约束集合 $\mathcal{M}$ 与「勿连」（cannot-link）约束集合 $\mathcal{C}$：

• $(\bm{x}_i, \bm{x}_{j}) \in \mathcal{M}$ 表示 $\bm{x}_i$ 与 $\bm{x}_{j}$ 相似；
• $(\bm{x}_i, \bm{x}_{j}) \in \mathcal{C}$ 表示 $\bm{x}_i$ 与 $\bm{x}_{j}$ 不相似。

显然我们希望相似的样本之间距离较小，于是可以通过求解下面的凸优化问题获得适当的度量矩阵 $\mathbf{M}$：

$$\min_{\mathbf{M}} \sum_{(\bm{x}_i, \bm{x}_{j}) \in \mathcal{M}}\left\lVert \bm{x}_i - \bm{x}_{j} \right\rVert_{\mathbf{M}}^2\quad \text{s.t.}\quad \sum_{(\bm{x}_i, \bm{x}_{k}) \in \mathcal{C}}\left\lVert \bm{x}_i - \bm{x}_{k} \right\rVert_{\mathbf{M}}^2 \ge 1,\, \mathbf{M} \succeq 0$$

其中约束 $\mathbf{M} \succeq 0$ 表示 $\mathbf{M}$ 必须是半正定的。上面的式子要求在不相似样本间的距离不小于 1 的前提下，使相似样本间的距离尽可能小。

不同的度量学习方法针对不同目标获得「好」的半正定对称距离度量矩阵 $\mathbf{M}$ ，若 $\mathbf{M}$ 是一个低秩矩阵，则通过对 $\mathbf{M}$ 进行特征值分解，总能找到一组正交基，其正交基数目为矩阵 $\mathbf{M}$ 的秩 $\operatorname{rank}(\mathbf{M})$ ，小于原属性数 $d$ 。于是，度量学习学得的结果可衍生出一个降维矩阵 $\mathbf{P} \in \mathbb{R}^{d \times \operatorname{rank}(\mathbf{M})}$，能用于降维之目的。

---

1. 实践中常通过对 $\mathbf{X}$ 进行奇异值分解代替对协方差矩阵的特征值分解。 ↩︎