背景
未标记样本
我们有训练样本集 D l = { ( x i , y i ) } i = 1 l D_{l}=\left\lbrace (\bm{x}_i, y_i) \right\rbrace_{i=1}^l D l = { ( x i , y i ) } i = 1 l l l l D u = { ( x i , y i ) } i = l + 1 l + u D_{u}=\left\lbrace (\bm{x}_i, y_i) \right\rbrace_{i=l+1}^{l+u} D u = { ( x i , y i ) } i = l + 1 l + u l ≪ u l \ll u l ≪ u u u u
若直接使用传统监督学习技术,则仅有 D l D_{l} D l D u D_{u} D u D l D_{l} D l D u D_{u} D u
一种简单的做法是将 D u D_u D u
可以用 D l D_l D l D u D_u D u D l D_l D l
这样的学习方法称为「主动学习」(active learning),其目标是使用尽可能少的「查询」(query)来获得尽可能好的性能。
主动学习引入了额外的专家知识,通过与外界的交互来将部分未标记样本转变为有标记样本。若不与专家交互,没有获得额外信息,一样能利用未标记样本来提高泛化性能。
未标记样本虽并未直接包含标记信息,但若它们与有标记样本是从同样的数据源 i.i.d. 采样而来,则它们所包含的关于数据分布的信息对建立模型大有裨益。
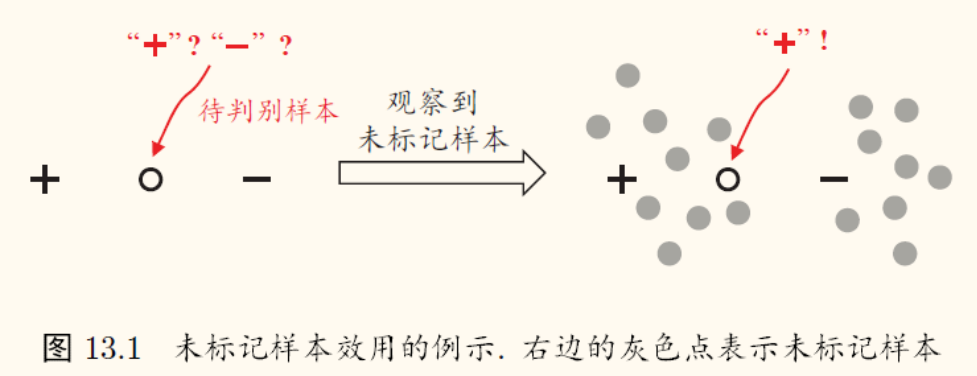
如下图所示,若基于图中的一个正例和一个反例,由于待判别的样本恰处于两者中间,大体上只能随机猜测。若能观察图中的未标记样本,可以有把握地判别为正例:
让学习器不依赖外界交互、自动地利用未标记样本来提升学习性能,就是半监督学习 (semi-supervised learning)。
要利用未标记样本,必然要做一些将未标记样本所揭示的数据分布信息与类别标记相联系的假设。
最常见的是「聚类假设」(cluster assumption),即假设数据存在簇结构,同一个簇的样本属于同一个类别。上图就是基于聚类假设来利用未标记样本。
另一种常见假设是「流形假设」(manifold assumption),即假设数据分布在一个流形结构上,邻近的样本具有相似的输出值。「邻近」程度常用「相似」程度来刻画,因此流形假设可以看作是聚类假设的推广,而且因为对于输出值没有限制,因此比聚类假设适用范围更广。
这两个假设本质都是「相似的样本具有相似的输出」这个基本假设。
半监督学习可以进一步划分为:
纯半监督学习 (pure semi-supervised learning):假定训练数据中的未标记样本并非待预测的数据;直推学习 (transductive learning):假定学习过程中所考虑的未标记样本恰是待预测数据,学习的目的就是在这些未标记样本上获得最优泛化性能。
直观来说,纯半监督学习基于「开放世界」假设,希望学得模型能适用于训练过程中未观察到的数据;直推学习是基于「封闭世界」假设,仅试图对学习过程中观察到的未标记样本进行预测。
生成式方法
生成式方法 (generative methods)是直接基于生成式模型的方法。此类方法假设所有数据(无论有无标记),都是由同一个潜在模型「生成」的。
这个假设使得我们能通过潜在模型的参数将未标记数据和学习目标联系起来,未标记数据的标记可看作模型的缺失参数,通常可基于 EM 算法进行极大似然估计求解。
这类方法的区别主要在于生成式模型的假设,不同的模型假设将产生不同的方法。
给定样本 x \bm{x} x y ∈ Y y \in \mathcal{Y} y ∈ Y Y = { 1 , 2 , … , N } \mathcal{Y} = \left\lbrace 1, 2, \dots, N \right\rbrace Y = { 1 , 2 , … , N }
假设样本由高斯混合模型生成,且每个类别对应一个高斯混合成分,即数据样本基于如下概率密度生成:
p ( x ) = ∑ i = 1 N α i ⋅ p ( x ∣ μ i , Σ i ) p(\bm{x}) = \sum_{i=1}^{N} \alpha_i \cdot p(\bm{x} \mid \bm{\mu}_i, \bm{\Sigma}_i)
p ( x ) = i = 1 ∑ N α i ⋅ p ( x ∣ μ i , Σ i )
其中混合系数 α i ⩾ 0 , ∑ i = 1 N α i = 1 \alpha_i \ge 0,\, \displaystyle \sum_{i=1}^{N}\alpha_i = 1 α i ⩾ 0 , i = 1 ∑ N α i = 1 p ( x ∣ μ i , Σ i ) p(\bm{x} \mid \bm{\mu}_i, \bm{\Sigma}_i) p ( x ∣ μ i , Σ i ) x \bm{x} x i i i μ i , Σ i \bm{\mu}_i, \bm{\Sigma}_i μ i , Σ i p ( x ∣ μ i , Σ i ) p(\bm{x} \mid \bm{\mu}_i, \bm{\Sigma}_i) p ( x ∣ μ i , Σ i ) x \bm{x} x p ( x ∣ μ i , Σ i ) = 1 ( 2 π ) d / 2 ⋅ ∣ Σ i ∣ 1 / 2 ⋅ exp ( − 1 2 ( x − μ i ) ⊺ Σ i − 1 ( x − μ i ) ) p(\bm{x} \mid \bm{\mu}_i, \bm{\Sigma}_i) = \dfrac{1}{(2\pi)^{d/2} \cdot |\bm{\Sigma}_i|^{1/2}} \cdot \exp\left( -\frac{1}{2} (\bm{x} - \bm{\mu}_i)^\intercal \bm{\Sigma}_i^{-1} (\bm{x} - \bm{\mu}_i) \right) p ( x ∣ μ i , Σ i ) = ( 2 π ) d /2 ⋅ ∣ Σ i ∣ 1/2 1 ⋅ exp ( − 2 1 ( x − μ i ) ⊺ Σ i − 1 ( x − μ i ) )
令 f ( x ) ∈ Y f(\bm{x}) \in \mathcal{Y} f ( x ) ∈ Y f f f x \bm{x} x Θ ∈ { 1 , 2 , … , N } \Theta \in \left\lbrace 1, 2, \dots, N \right\rbrace Θ ∈ { 1 , 2 , … , N } x \bm{x} x
f ( x ) = arg max j ∈ Y p ( y = j ∣ x ) = arg max j ∈ Y ∑ i = 1 N p ( y = j , Θ = i ∣ x ) = arg max j ∈ Y ∑ i = 1 N p ( y = j ∣ Θ = i , x ) ⋅ p ( Θ = i ∣ x ) \begin{aligned}
f(\bm{x}) &= \argmax_{j \in \mathcal{Y}} p(y=j \mid \bm{x}) \\
&= \argmax_{j \in \mathcal{Y}} \sum_{i=1}^{N} p(y=j, \Theta=i \mid \bm{x}) \\
&= \argmax_{j \in \mathcal{Y}} \sum_{i=1}^{N} p(y=j \mid \Theta=i, \bm{x}) \cdot p(\Theta=i \mid \bm{x}) \\
\end{aligned}
f ( x ) = j ∈ Y arg max p ( y = j ∣ x ) = j ∈ Y arg max i = 1 ∑ N p ( y = j , Θ = i ∣ x ) = j ∈ Y arg max i = 1 ∑ N p ( y = j ∣ Θ = i , x ) ⋅ p ( Θ = i ∣ x )
其中
p ( Θ = i ∣ x ) = α i ⋅ p ( x ∣ μ i , Σ i ) ∑ k = 1 N α k ⋅ p ( x ∣ μ k , Σ k ) p(\Theta = i \mid \bm{x}) = \dfrac{\alpha_i \cdot p(\bm{x} \mid \bm{\mu}_i, \bm{\Sigma}_i)}{\sum\limits_{k=1}^{N} \alpha_k \cdot p(\bm{x} \mid \bm{\mu}_k, \bm{\Sigma}_k)}
p ( Θ = i ∣ x ) = k = 1 ∑ N α k ⋅ p ( x ∣ μ k , Σ k ) α i ⋅ p ( x ∣ μ i , Σ i )
为样本 x \bm{x} x i i i p ( y = j ∣ Θ = i , x ) p(y=j \mid \Theta=i, \bm{x}) p ( y = j ∣ Θ = i , x ) x \bm{x} x i i i j j j
由于假设每个类别对应一个高斯混合成分,因此 p ( y = j ∣ Θ = i , x ) p(y = j \mid \Theta = i, \bm{x}) p ( y = j ∣ Θ = i , x ) x \bm{x} x Θ \Theta Θ p ( y = j ∣ Θ = i ) p(y = j \mid \Theta = i) p ( y = j ∣ Θ = i )
不失一般性,假定第 i i i i i i p ( y = j ∣ Θ = i ) = 1 p(y = j \mid \Theta = i) = 1 p ( y = j ∣ Θ = i ) = 1 i = j i = j i = j p ( y = j ∣ Θ = i ) = 0 p(y = j \mid \Theta = i) = 0 p ( y = j ∣ Θ = i ) = 0
上式估计 P ( y = j ∣ Θ = i , x ) P(y = j \mid \Theta = i, \bm{x}) P ( y = j ∣ Θ = i , x ) p ( Θ = i ∣ x ) p(\Theta = i \mid \bm{x}) p ( Θ = i ∣ x )
假设所有样本独立同分布,且都是有同一个高斯混合模型生成的。用极大似然法来估计高斯混合模型的参数 { ( α i , μ i , Σ i ) ∣ 1 ⩽ i ⩽ N } , D l ∪ D u \left\lbrace (\alpha_i, \bm{\mu}_i, \bm{\Sigma}_i) \mid 1 \le i \le N \right\rbrace,\, D_l \cup D_u { ( α i , μ i , Σ i ) ∣ 1 ⩽ i ⩽ N } , D l ∪ D u
L L ( D l ∪ D u ) = ∑ ( x j , y j ) ∈ D l ln ( ∑ i = 1 N α i ⋅ p ( x j ∣ μ i , Σ i ) ⋅ p ( y j ∣ Θ = i , x j ) ) = + ∑ x j ∈ D u ln ( ∑ i = 1 N α i ⋅ p ( x j ∣ μ i , Σ i ) ) \begin{aligned}
LL(D_l \cup D_u) &= \sum_{(\bm{x}_{j}, y_{j}) \in D_l} \ln \left( \sum_{i=1}^N \alpha_i \cdot p(\bm{x}_{j} \mid \bm{\mu}_i, \bm{\Sigma}_i) \cdot p(y_{j} \mid \Theta = i, \bm{x}_{j}) \right) \\
&\phantom{=}+ \sum_{\bm{x}_{j} \in D_u} \ln \left( \sum_{i=1}^N \alpha_i \cdot p(\bm{x}_{j} \mid \bm{\mu}_i, \bm{\Sigma}_i) \right)
\end{aligned}
LL ( D l ∪ D u ) = ( x j , y j ) ∈ D l ∑ ln ( i = 1 ∑ N α i ⋅ p ( x j ∣ μ i , Σ i ) ⋅ p ( y j ∣ Θ = i , x j ) ) = + x j ∈ D u ∑ ln ( i = 1 ∑ N α i ⋅ p ( x j ∣ μ i , Σ i ) )
上面两项分别是:
基于有标记数据 D l D_l D l
基于未标记数据 D u D_u D u
高斯混合模型参数估计可用 EM 算法求解,迭代更新式如下:
E 步:根据当前模型参数计算未标记样本 x j \bm{x}_{j} x j
γ j i = α i ⋅ p ( x j ∣ μ i , Σ i ) ∑ k = 1 N α k ⋅ p ( x j ∣ μ k , Σ k ) \gamma_{ji} = \dfrac{\alpha_i \cdot p(\bm{x}_{j} \mid \bm{\mu}_i, \bm{\Sigma}_i)}{\sum\limits_{k=1}^{N} \alpha_k \cdot p(\bm{x}_{j} \mid \bm{\mu}_k, \bm{\Sigma}_k)}
γ j i = k = 1 ∑ N α k ⋅ p ( x j ∣ μ k , Σ k ) α i ⋅ p ( x j ∣ μ i , Σ i )
M 步:基于 γ j i \gamma_{ji} γ j i l i l_i l i i i i
μ i = 1 ∑ x j ∈ D u γ j i + l i ( ∑ x j ∈ D u γ j i x j + ∑ ( x j , y j ) ∈ D l , y j = i x j ) Σ i = 1 ∑ x j ∈ D u γ j i + l i ( ∑ x j ∈ D u γ j i ( x j − μ i ) ( x j − μ i ) ⊺ + ∑ ( x j , y j ) ∈ D l , y j = i ( x j − μ i ) ( x j − μ i ) ⊺ ) α i = 1 m ( ∑ x j ∈ D u γ j i + l i ) \begin{aligned}
\bm{\mu}_i &= \dfrac{1}{\sum_{\bm{x}_{j} \in D_u}\gamma_{ji} + l_i} \left( \sum_{\bm{x}_{j} \in D_u} \gamma_{ji} \bm{x}_{j} + \sum_{(\bm{x}_{j}, y_{j}) \in D_l, y_{j} = i} \bm{x}_{j} \right) \\
\bm{\Sigma}_i &= \dfrac{1}{\sum_{\bm{x}_{j} \in D_u}\gamma_{ji} + l_i} \left( \sum_{\bm{x}_{j} \in D_u} \gamma_{ji} (\bm{x}_{j} - \bm{\mu}_i)(\bm{x}_{j} - \bm{\mu}_i)^\intercal + \sum_{(\bm{x}_{j}, y_{j}) \in D_l, y_{j} = i} (\bm{x}_{j} - \bm{\mu}_i)(\bm{x}_{j} - \bm{\mu}_i)^\intercal \right) \\
\alpha_i &= \dfrac{1}{m} \left( \sum_{\bm{x}_{j} \in D_u} \gamma_{ji} + l_i \right)
\end{aligned}
μ i Σ i α i = ∑ x j ∈ D u γ j i + l i 1 x j ∈ D u ∑ γ j i x j + ( x j , y j ) ∈ D l , y j = i ∑ x j = ∑ x j ∈ D u γ j i + l i 1 x j ∈ D u ∑ γ j i ( x j − μ i ) ( x j − μ i ) ⊺ + ( x j , y j ) ∈ D l , y j = i ∑ ( x j − μ i ) ( x j − μ i ) ⊺ = m 1 x j ∈ D u ∑ γ j i + l i
以上过程不断迭代直至收敛,即可获得模型参数。然后由 p ( Θ = i ∣ x ) p(\Theta = i \mid \bm{x}) p ( Θ = i ∣ x ) f ( x ) f(\bm{x}) f ( x )
将上述过程中的高斯混合模型换成混合专家模型,朴素贝叶斯模型等即可推导出其他的生成式半监督学习算法。
此类方法简单、易于实现,在有标记数据极少的情形下往往比其他方法性能更好。
然而,此类方法有一个关键:模型假设必须准确,即假设的生成式模型必须与真实数据分布吻合;否则利用未标记数据反而会显著降低泛化性能。
半监督支持向量机
半监督支持向量机 (Semi-Supervised Support Vector Machine, S3VM)是支持向量机在半监督学习上的推广。
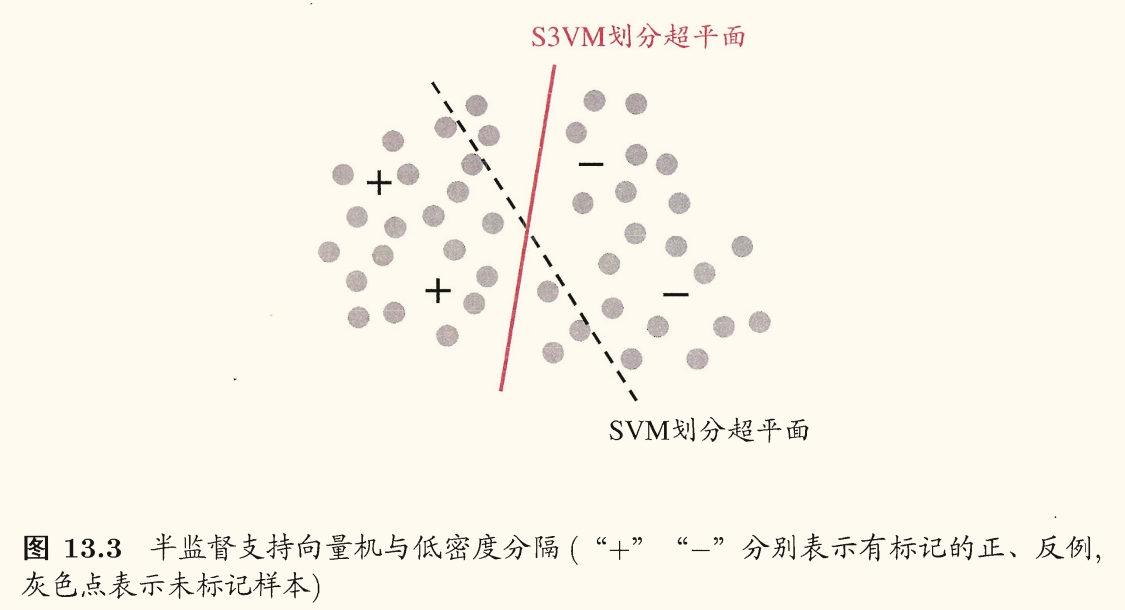
在不考虑未标记样本时,支持向量机试图找到最大间隔划分超平面。而在考虑未标记样本后,S3VM 试图找到能将两类有标记样本分开,且穿过数据低密度区域的划分超平面,如下图所示:
这里的基本假设是「低密度分隔」(low-density separation),这是聚类假设在考虑线性超平面划分后的推广。
S3VM 最著名的是 TSVM(Transductive Support Vector Machine)。
TSVM 试图考虑对无标记样本进行各种可能的标记指派(label assignment),即尝试将每个未标记样本分别作为正例或反例,然后在所有这些结果中,寻求一个在所有样本(包括有标记样本和进行了标记指派的未标记样本)上间隔最大化的划分超平面。一旦划分超平面得以确定,未标记样本的最终标记指派就是其预测结果。
下面是形式化的说明。给定训练数据 D l ∪ D u D_l \cup D_u D l ∪ D u D l = { ( x i , y i ) } i = 1 l D_l = \left\lbrace (\bm{x}_i, y_i) \right\rbrace_{i=1}^l D l = { ( x i , y i ) } i = 1 l D u = { x i } i = l + 1 l + u D_u = \left\lbrace \bm{x}_i \right\rbrace_{i=l+1}^{l+u} D u = { x i } i = l + 1 l + u y i ∈ { − 1 , 1 } y_i \in \left\lbrace -1, 1 \right\rbrace y i ∈ { − 1 , 1 } m = l + u m = l + u m = l + u
TSVM 的学习目标是为 D u D_u D u y ^ = ( y ^ l + 1 , … , y ^ l + u ) , y ^ i ∈ { − 1 , 1 } \hat{\bm{y}} = (\hat{y}_{l+1}, \dots, \hat{y}_{l+u}),\, \hat{y}_i \in \left\lbrace -1, 1 \right\rbrace y ^ = ( y ^ l + 1 , … , y ^ l + u ) , y ^ i ∈ { − 1 , 1 }
min w , b , y ^ , ξ 1 2 ∥ w ∥ 2 2 + C l ∑ i = 1 l ξ i + C u ∑ i = l + 1 m ξ i s.t. y i ( w ⊺ x i + b ) ⩾ 1 − ξ i , ∀ i = 1 , 2 , … , l y ^ i ( w ⊺ x i + b ) ⩾ 1 − ξ i , ∀ i = l + 1 , … , m ξ i ⩾ 0 , ∀ i = 1 , 2 , … , m \begin{aligned}
\min_{\bm{w}, b, \hat{\bm{y}}, \bm{\xi}} &\dfrac{1}{2} \left\lVert \bm{w} \right\rVert_2^2 + C_l \sum_{i=1}^l \xi_i + C_u \sum_{i=l+1}^m \xi_i\\
\quad \text{s.t.}\quad & y_i(\bm{w}^\intercal \bm{x}_i + b) \ge 1 - \xi_i,\, \forall i = 1, 2, \dots, l\\
& \hat{y}_i(\bm{w}^\intercal \bm{x}_i + b) \ge 1 - \xi_i,\, \forall i = l+1, \dots, m\\
& \xi_i \ge 0,\, \forall i = 1, 2, \dots, m
\end{aligned}
w , b , y ^ , ξ min s.t. 2 1 ∥ w ∥ 2 2 + C l i = 1 ∑ l ξ i + C u i = l + 1 ∑ m ξ i y i ( w ⊺ x i + b ) ⩾ 1 − ξ i , ∀ i = 1 , 2 , … , l y ^ i ( w ⊺ x i + b ) ⩾ 1 − ξ i , ∀ i = l + 1 , … , m ξ i ⩾ 0 , ∀ i = 1 , 2 , … , m
其中
( w , b ) (\bm{w}, b) ( w , b ) ξ \bm{\xi} ξ
ξ ( i = 1 , … , l ) \xi\,(i = 1, \dots, l) ξ ( i = 1 , … , l ) ξ ( i = l + 1 , … , m ) \xi\,(i = l+1, \dots, m) ξ ( i = l + 1 , … , m )
C l , C u C_l, C_u C l , C u
TSVM 采用局部搜索迭代寻找上式的近似解。
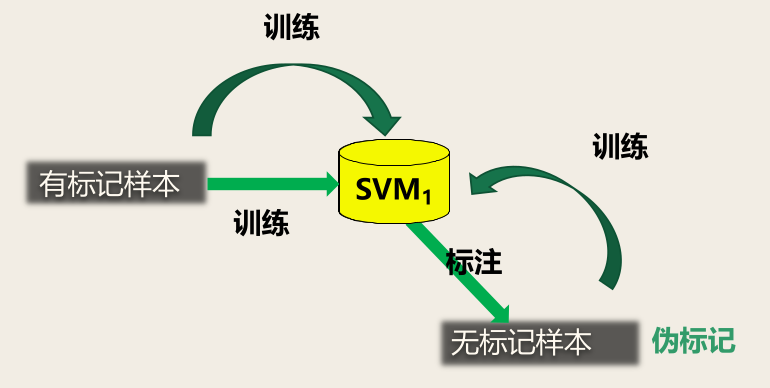
具体来说,它先利用有标记样本学得一个 SVM,即忽略上式关于 D u D_u D u y ^ \hat{\bm{y}} y ^
此时 y ^ \hat{\bm{y}} y ^ C u C_u C u C l C_l C l
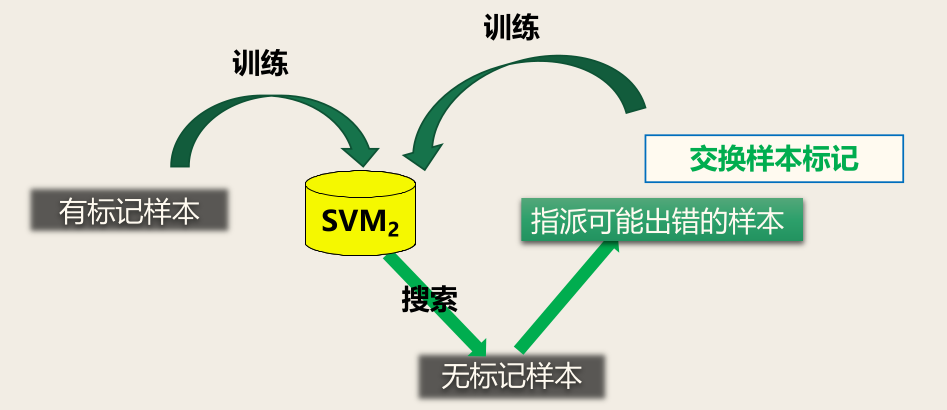
接下来 TSVM 找出两个标记指派为异类,且很可能发生错误的未标记样本,交换它们的标记,重新基于上式求解出更新后的划分超平面和松弛向量……
标记指派调整完成后,逐渐增大 C u C_u C u C u = C l C_u = C_l C u = C l
TSVM 算法流程
蓝框中,若存在一对未标记样本 x i , x j \bm{x}_i, \bm{x}_{j} x i , x j y ^ i , y ^ j \hat{y}_i, \hat{y}_{j} y ^ i , y ^ j ξ i + ξ j > 2 \xi_i + \xi_{j} > 2 ξ i + ξ j > 2 y ^ i \hat{y}_i y ^ i y ^ j \hat{y}_{j} y ^ j
在对未标记样本进行标记指派及调整的过程中,有可能出现类别不平衡问题,即某类的样本远多于另一类,这将对 SVM 的训练造成困扰。为了减轻类别不平衡性所造成的不利影响,可对上面的算法稍加改进:
将优化目标中的 C u C_u C u C u + , C u − C_u^{+}, C_u^{-} C u + , C u − C u + = u − u + C u − C_u^{+} = \dfrac{u_{-}}{u_{+}}C_u^{-} C u + = u + u − C u − u + , u − u_{+}, u_{-} u + , u −
搜寻标记指派可能出错的每一对未标记样本进行调整,仍是一个涉及巨大计算开销的大规模优化问题。因此,半监督 SVM 研究的一个重点是如何设计出高效的优化求解策略。
图半监督学习
给定一个数据集,我们可将其映射为一个图,数据集中每个样本对应于图中一个结点,若两个样本之间的相似度很高 (或相关性很强),则对应的结点之间存在一条边,边的强度 (strength)正比于样本之间的相似度 (或相关性)。
我们可将有标记样本所对应的结点想象为染过色,而未标记样本所对应的结点则尚未染色。于是,半监督学习就对应于「颜色」在图上扩散或传播的过程。
由于一个图对应了一个矩阵,这就使得我们能基于矩阵运算来进行半监督学习算法的推导与分析。
二分类问题
先基于 D l ∪ D u D_l \cup D_u D l ∪ D u G = ( V , E ) G = (V, E) G = ( V , E ) V = { x 1 , … , x l + u } V = \left\lbrace \bm{x}_1, \dots, \bm{x}_{l+u} \right\rbrace V = { x 1 , … , x l + u }
边集 E E E
W i j = { exp ( − ∥ x i − x j ∥ 2 2 σ 2 ) , if i ≠ j 0 , otherwise \mathbf{W}_{ij} = \begin{cases}
\exp\left( -\dfrac{\| \bm{x}_i - \bm{x}_j \|^2}{2\sigma^2} \right), & \text{if } i \ne j \\
0, & \text{otherwise}
\end{cases}
W ij = ⎩ ⎨ ⎧ exp ( − 2 σ 2 ∥ x i − x j ∥ 2 ) , 0 , if i = j otherwise
其中 i , j ∈ { 1 , 2 , … , m } i, j \in \left\lbrace 1, 2, \dots, m \right\rbrace i , j ∈ { 1 , 2 , … , m } σ \sigma σ
假定从图 G = ( V , E ) G = (V, E) G = ( V , E ) f : V → R f\colon V \to \R f : V → R y i = sign ( f ( x i ) ) , y i ∈ { − 1 , 1 } y_i = \operatorname{sign}(f(\bm{x}_i)), y_i \in \left\lbrace -1, 1 \right\rbrace y i = sign ( f ( x i )) , y i ∈ { − 1 , 1 }
直观上看,相似的样本应具有相似的标记,于是可定义关于 f f f 能量函数 (energy function):
E ( f ) = 1 2 ∑ i = 1 m ∑ j = 1 m W i j ( f ( x i ) − f ( x j ) ) 2 = 1 2 ( ∑ i = 1 m d i f 2 ( x i ) + ∑ j = 1 m d j f 2 ( x j ) − 2 ∑ i = 1 m ∑ j = 1 m W i j f ( x i ) f ( x j ) ) = ∑ i = 1 m d i f 2 ( x i ) − ∑ i = 1 m ∑ j = 1 m W i j f ( x i ) f ( x j ) = f ⊺ ( D − W ) f \begin{aligned}
E(f) &= \dfrac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \mathbf{W}_{ij} (f(\bm{x}_i) - f(\bm{x}_j))^2 \\
&= \dfrac{1}{2} \left( \sum_{i=1}^{m} d_i f^2(\bm{x}_i) + \sum_{j=1}^{m} d_j f^2(\bm{x}_j) - 2 \sum_{i=1}^{m} \sum_{j=1}^{m} \mathbf{W}_{ij} f(\bm{x}_i) f(\bm{x}_j) \right)\\
&= \sum_{i=1}^{m}d_i f^2 (\bm{x}_i) - \sum_{i=1}^{m} \sum_{j=1}^{m} \mathbf{W}_{ij} f(\bm{x}_i) f(\bm{x}_j)\\
&= \bm{f}^\intercal(\mathbf{D} - \mathbf{W}) \bm{f}
\end{aligned}
E ( f ) = 2 1 i = 1 ∑ m j = 1 ∑ m W ij ( f ( x i ) − f ( x j ) ) 2 = 2 1 ( i = 1 ∑ m d i f 2 ( x i ) + j = 1 ∑ m d j f 2 ( x j ) − 2 i = 1 ∑ m j = 1 ∑ m W ij f ( x i ) f ( x j ) ) = i = 1 ∑ m d i f 2 ( x i ) − i = 1 ∑ m j = 1 ∑ m W ij f ( x i ) f ( x j ) = f ⊺ ( D − W ) f
其中 f = ( f l ⊺ f u ⊺ ) ⊺ \bm{f} = (\bm{f}_l^\intercal \bm{f}_u^\intercal)^\intercal f = ( f l ⊺ f u ⊺ ) ⊺ f l = ( f ( x 1 ) ; … ; f ( x l ) ) \bm{f}_l = (f(\bm{x}_1); \dots; f(\bm{x}_l)) f l = ( f ( x 1 ) ; … ; f ( x l )) f u = ( f ( x l + 1 ) ; … ; f ( x l + u ) ) \bm{f}_u = (f(\bm{x}_{l+1}); \dots; f(\bm{x}_{l+u})) f u = ( f ( x l + 1 ) ; … ; f ( x l + u )) f f f D = diag ( d 1 , … , d l + u ) \mathbf{D} = \operatorname{diag}(d_1, \dots, d_{l+u}) D = diag ( d 1 , … , d l + u ) d i = ∑ j = 1 l + u W i j d_i = \sum_{j=1}^{l+u}\mathbf{W}_{ij} d i = ∑ j = 1 l + u W ij W \mathbf{W} W i i i
具有最小能量的函数 f f f f ( x i ) = y i f(\bm{x}_i) = y_i f ( x i ) = y i Δ f = 0 \bm{\Delta} \bm{f} = \bm{0} Δ f = 0 Δ = D − W \bm{\Delta} = \mathbf{D} - \mathbf{W} Δ = D − W 拉普拉斯矩阵 (Laplacian matrix)。
采用分块矩阵表示方法,有
W = [ W l l W l u W u l W u u ] , D = [ D l l 0 l u 0 u l D u u ] \mathbf{W} = \begin{bmatrix}
\mathbf{W}_{ll} & \mathbf{W}_{lu} \\
\mathbf{W}_{ul} & \mathbf{W}_{uu}
\end{bmatrix}, \quad \mathbf{D} = \begin{bmatrix}
\mathbf{D}_{ll} & \mathbf{0}_{lu} \\
\mathbf{0}_{ul} & \mathbf{D}_{uu}
\end{bmatrix}
W = [ W l l W u l W l u W uu ] , D = [ D l l 0 u l 0 l u D uu ]
则能量函数可写为
E ( f ) = ( f l ⊺ f u ⊺ ) [ D l l − W l l − W l u − W u l D u u − W u u ] [ f l f u ] = f l ⊺ ( D l l − W l l ) f l + f u ⊺ ( D u u − W u u ) f u − 2 f u ⊺ W u l f l \begin{aligned}
E(f) &= (\bm{f}_l^\intercal \bm{f}_u^\intercal) \begin{bmatrix}
\mathbf{D}_{ll} - \mathbf{W}_{ll} & -\mathbf{W}_{lu} \\
-\mathbf{W}_{ul} & \mathbf{D}_{uu} - \mathbf{W}_{uu}
\end{bmatrix} \begin{bmatrix}
\bm{f}_l \\
\bm{f}_u
\end{bmatrix} \\
&= \bm{f}_l^\intercal (\mathbf{D}_{ll} - \mathbf{W}_{ll}) \bm{f}_l + \bm{f}_u^\intercal (\mathbf{D}_{uu} - \mathbf{W}_{uu}) \bm{f}_u - 2 \bm{f}_u^\intercal \mathbf{W}_{ul} \bm{f}_l
\end{aligned}
E ( f ) = ( f l ⊺ f u ⊺ ) [ D l l − W l l − W u l − W l u D uu − W uu ] [ f l f u ] = f l ⊺ ( D l l − W l l ) f l + f u ⊺ ( D uu − W uu ) f u − 2 f u ⊺ W u l f l
由 ∂ E ( f ) ∂ f u = 0 \dfrac{\partial E(f)}{\partial \bm{f}_u} = \bm{0} ∂ f u ∂ E ( f ) = 0
f u = ( D u u − W u u ) − 1 W u l f l \bm{f}_u = (\mathbf{D}_{uu} - \mathbf{W}_{uu})^{-1} \mathbf{W}_{ul} \bm{f}_l
f u = ( D uu − W uu ) − 1 W u l f l
令
P = D − 1 W = [ D l l − 1 0 l u 0 u l D u u − 1 ] [ W l l W l u W u l W u u ] = [ D l l − 1 W l l D l l − 1 W l u D u u − 1 W u l D u u − 1 W u u ] \begin{aligned}
\mathbf{P} &= \mathbf{D}^{-1} \mathbf{W} = \begin{bmatrix}
\mathbf{D}_{ll}^{-1} & \bm{0}_{lu}\\
\bm{0}_{ul} & \mathbf{D}_{uu}^{-1}
\end{bmatrix} \begin{bmatrix}
\mathbf{W}_{ll} & \mathbf{W}_{lu} \\
\mathbf{W}_{ul} & \mathbf{W}_{uu}
\end{bmatrix} \\
&= \begin{bmatrix}
\mathbf{D}_{ll}^{-1} \mathbf{W}_{ll} & \mathbf{D}_{ll}^{-1} \mathbf{W}_{lu} \\
\mathbf{D}_{uu}^{-1} \mathbf{W}_{ul} & \mathbf{D}_{uu}^{-1} \mathbf{W}_{uu}
\end{bmatrix}
\end{aligned}
P = D − 1 W = [ D l l − 1 0 u l 0 l u D uu − 1 ] [ W l l W u l W l u W uu ] = [ D l l − 1 W l l D uu − 1 W u l D l l − 1 W l u D uu − 1 W uu ]
即 P u u = D u u − 1 W u u , P u l = D u u − 1 W u l \mathbf{P}_{uu} = \mathbf{D}_{uu}^{-1} \mathbf{W}_{uu},\, \mathbf{P}_{ul} = \mathbf{D}_{uu}^{-1} \mathbf{W}_{ul} P uu = D uu − 1 W uu , P u l = D uu − 1 W u l
f u = ( D u u ( I − D u u − 1 W u u ) ) − 1 W u l f l = ( I − P u u ) − 1 D u u − 1 W u l f l = ( I − P u u ) − 1 P u l f l \begin{aligned}
\bm{f}_u &= (\mathbf{D}_{uu}(\mathbf{I} - \mathbf{D}_{uu}^{-1} \mathbf{W}_{uu}))^{-1} \mathbf{W}_{ul} \bm{f}_l\\
&= (\mathbf{I} - \mathbf{P}_{uu})^{-1} \mathbf{D}_{uu}^{-1} \mathbf{W}_{ul} \bm{f}_l\\
&= (\mathbf{I} - \mathbf{P}_{uu})^{-1} \mathbf{P}_{ul} \bm{f}_l
\end{aligned}
f u = ( D uu ( I − D uu − 1 W uu ) ) − 1 W u l f l = ( I − P uu ) − 1 D uu − 1 W u l f l = ( I − P uu ) − 1 P u l f l
于是,将 D l D_l D l f l = ( y 1 ; … ; y l ) f_l = (y_1; \dots; y_l) f l = ( y 1 ; … ; y l ) f u \bm{f}_u f u
多分类问题
上面是针对二分类问题的「单步式」标记传播(label propagation)方法,下面会介绍一个适用于多分类问题的「迭代式」标记传播方法。
假定 y i ∈ Y y_i \in \mathcal{Y} y i ∈ Y D l ∪ D u D_l \cup D_u D l ∪ D u G = ⟨ V , E ⟩ G = \left\langle V, E \right\rangle G = ⟨ V , E ⟩
定义一个 ( l + u ) × ∣ Y ∣ (l + u) \times |\mathcal{Y}| ( l + u ) × ∣ Y ∣ F = ( F 1 ⊺ , … , F ∣ Y ∣ ⊺ ) ⊺ \mathbf{F} = (\mathbf{F}_1^\intercal, \dots, \mathbf{F}_{|\mathcal{Y}|}^\intercal)^\intercal F = ( F 1 ⊺ , … , F ∣ Y ∣ ⊺ ) ⊺ F i = ( F i 1 , … , F i ∣ Y ∣ ) \mathbf{F}_i = (\mathbf{F}_{i 1}, \dots, \mathbf{F}_{i |\mathcal{Y}|}) F i = ( F i 1 , … , F i ∣ Y ∣ ) x i \bm{x}_i x i
y i = arg max 1 ⩽ j ⩽ ∣ Y ∣ F i j y_i = \argmax_{1 \le j \le |\mathcal{Y}|} \mathbf{F}_{ij}
y i = 1 ⩽ j ⩽ ∣ Y ∣ arg max F ij
对于 i = 1 , … , m ; j = 1 , … , ∣ Y ∣ i = 1, \dots, m;\; j = 1, \dots, |\mathcal{Y}| i = 1 , … , m ; j = 1 , … , ∣ Y ∣ F \mathbf{F} F
F ( 0 ) = Y i j = { 1 , if ( 1 ⩽ i ⩽ l ) and ( y i = j ) 0 , otherwise \mathbf{F}(0) = \mathbf{Y}_{ij} = \begin{cases}
1, & \text{if } (1 \le i \le l) \text{ and } (y_i = j)\\
0, & \text{otherwise}
\end{cases}
F ( 0 ) = Y ij = { 1 , 0 , if ( 1 ⩽ i ⩽ l ) and ( y i = j ) otherwise
即 Y \mathbf{Y} Y l l l l l l
基于 W \mathbf{W} W S = D − 1 / 2 W D − 1 / 2 \mathbf{S} = \mathbf{D}^{-1 / 2} \mathbf{W} \mathbf{D}^{-1 / 2} S = D − 1/2 W D − 1/2 D − 1 / 2 = diag ( 1 d 1 , … , 1 d l + u ) \mathbf{D}^{-1 / 2} = \operatorname{diag}\left( \dfrac{1}{\sqrt{d_1}}, \dots, \dfrac{1}{\sqrt{d_{l+u}}} \right) D − 1/2 = diag ( d 1 1 , … , d l + u 1 )
于是有迭代计算式
F ( t + 1 ) = α S F ( t ) + ( 1 − α ) Y \mathbf{F}(t + 1) = \alpha \mathbf{S} \mathbf{F}(t) + (1 - \alpha) \mathbf{Y}
F ( t + 1 ) = α SF ( t ) + ( 1 − α ) Y
其中 α ∈ ( 0 , 1 ) \alpha \in (0, 1) α ∈ ( 0 , 1 ) S F ( t ) \mathbf{S} \mathbf{F}(t) SF ( t ) Y \mathbf{Y} Y
基于这个迭代计算式,迭代至收敛可得
F ∗ = lim t → ∞ F ( t ) = ( 1 − α ) ( I − α S ) − 1 Y \mathbf{F}^{*} = \lim\limits_{t \to \infty} \mathbf{F}(t) = (1 - \alpha)(\mathbf{I} - \alpha \mathbf{S})^{-1} \mathbf{Y}
F ∗ = t → ∞ lim F ( t ) = ( 1 − α ) ( I − α S ) − 1 Y
由 F ∗ \mathbf{F}^{*} F ∗ ( y ^ l + 1 , … , y ^ l + u ) (\hat{y}_{l+1}, \dots, \hat{y}_{l + u}) ( y ^ l + 1 , … , y ^ l + u )
算法描述如下:
上面的算法对应于「正则化框架」
min F 1 2 ( ∑ i , j = 1 l + u W i j ∥ 1 d i F i − 1 d j F j ∥ 2 ) + μ ∑ i = 1 l ∥ F i − Y i ∥ 2 \min_{\mathbf{F}} \dfrac{1}{2} \left( \sum_{i, j = 1}^{l + u} \mathbf{W}_{ij} \left\lVert \dfrac{1}{\sqrt{d_i}} \mathbf{F}_i - \dfrac{1}{\sqrt{d_{j}}} \mathbf{F}_{j} \right\rVert^2 \right) + \mu \sum_{i = 1}^l \left\lVert \mathbf{F}_i - \mathbf{Y}_i \right\rVert^2
F min 2 1 i , j = 1 ∑ l + u W ij d i 1 F i − d j 1 F j 2 + μ i = 1 ∑ l ∥ F i − Y i ∥ 2
其中 μ > 0 \mu > 0 μ > 0
μ = 1 − α α \mu = \dfrac{1 - \alpha}{\alpha} μ = α 1 − α F ∗ \mathbf{F}^{*} F ∗
上式第二项是迫使学得结果在有标记样本上的预测与真实标记E ( f ) = f ⊺ ( D − W ) f E(f) = \bm{f}^\intercal(\mathbf{D} - \mathbf{W}) \bm{f} E ( f ) = f ⊺ ( D − W ) f E ( f ) E(f) E ( f )
图半监督学习方法在概念上相当清晰,且易于通过对所涉矩阵运算的分析来探索算法性质。
但此类算法的缺陷也相当明显,
其存储开销高 ;
由于构图过程仅能考虑训练样本集 ,难以判知新样本在图中的位置,因此,在接收到新样本时,或是将其加入原数据集对图进行重构并重新进行标记传播,或是需引入额外的预测机制。
基于分歧的方法
与生成式方法、半监督 SVM、图半监督学习等基于单学习器利用未标记数据不同,基于分歧的方法(disagreement-based methods)使用多学习器,而学习器之间的分歧 (disagreement/diversity)对未标记数据的利用至关重要。
协同训练 (co-training)是基于分歧的方法的重要代表,它最初是基于「多视图」数据设计的,因此也被看作「多视图学习」(multi-view learning)的代表。
在不少现实应用中,一个数据对象往往同时拥有多个「属性集」(attribute set),每个属性集就构成了一个视图 (view)。例如对一部电影来说,它拥有多个属性集:图像画面信息所对应的属性集、声音信息所对应的属性集、字幕信息所对应的属性集等。每个属性集都可看作一个视图。
为简化讨论,暂且仅考虑图像画面属性集所构成的视图和声音属性集所构成的视图。于是一个电影片段可表示为样本 ( ⟨ x 1 , x 2 ⟩ , y ) \left(\left\langle \bm{x}^1, \bm{x}^2 \right\rangle, y\right) ( ⟨ x 1 , x 2 ⟩ , y ) x i \bm{x}^i x i i i i x 1 \bm{x}^1 x 1 x 2 \bm{x}^2 x 2 y y y ( ⟨ x 1 , x 2 ⟩ , y ) \left(\left\langle \bm{x}^1, \bm{x}^2 \right\rangle, y\right) ( ⟨ x 1 , x 2 ⟩ , y )
假设不同视图具有相容性 (compatibility),即其所包含的关于输出空间 Y \mathcal{Y} Y Y 1 , Y 2 \mathcal{Y}^1, \mathcal{Y}^2 Y 1 , Y 2 Y = Y 1 = Y 2 \mathcal{Y} = \mathcal{Y}^1 = \mathcal{Y}^2 Y = Y 1 = Y 2
在相容性的基础上,不同视图信息的互补性 会给学习器的构建带来很多便利。
协同训练很好地利用了多视图的「相容互补性」。假设数据拥有两个「充分」(sufficient)且「条件独立」的视图:
充分:指每个视图都包含足以产生最优学习器的信息;
条件独立:指在给定类别标记条件下两个视图独立。
在此情形下,可用一个简单的方法利用未标记数据:
首先在每个视图上基于有标记样本分别训练出一个分类器,
然后让每个分类器分别去挑选自己「最有把握的」未标记样本赋予伪标记,并将伪标记样本提供给另一个分类器作为新增的有标记样本用于训练更新
这个「互相学习、共同进步」的过程不断迭代进行,直到两个分类器都不再发生变化,或达到预先设定的迭代轮数为止
若在每轮学习都考察分类器在所有未标记样本上的分类置信度,会有很大的计算开销,因此在算法中使用了未标记样本缓冲池。
分类置信度的估计则因基学习算法 L \mathfrak{L} L
理论证明显示出,若两个视图充分且条件独立,则可利用未标记样本通过协同训练将弱分类器的泛化性能提升到任意高。
不过视图的条件独立性在现实任务中通常很难满足,因此性能提升幅度不会那么大。但研究表明即便在更弱的条件下,协同训练仍可有效地提升弱分类器的性能。
协同训练算法本身是为多视图数据而设计的,但此后出现了一些能在单视图数据上使用的变体算法。它们或是使用不同的学习算法、或使用不同的数据采样、甚至使用不同的参数设置来产生不同的学习器,也能有效地利用未标记数据来提升性能。
后续理论研究发现,此类算法事实上无需数据拥有多视图,仅需弱学习器之间具有显著的分歧(或差异) ,即可通过相互提供伪标记样本的方式来提高泛化性能。
基于分歧的方法只需采用合适的基学习器 ,就较少受到模型假设、损失函数非凸性和数据规模问题的影响,学习方法简单有效、理论基础相对坚实、适用范围较为广泛。
为了使用此类方法,需能生成具有显著分歧、性能尚可的多个学习器,但当有标记样本很少 、尤其是数据不具有多视图时,要做到这一点并不容易。
半监督聚类
聚类是一种典型的无监督学习任务,然而在现实聚类任务中我们往往能获得一些额外的监督信息,于是可通过「半监督聚类」(semi-supervised clustering)来利用监督信息以获得更好的聚类效果。
聚类任务中获得的监督信息大致有两种类型:
第一种类型是「必连」(must-link)与「勿连」(cannot-link)约束,前者是指样本必属于同一个簇,后者则是指样本必不属于同一个簇;
第二种类型的监督信息则是少量的有标记样本。
第一类
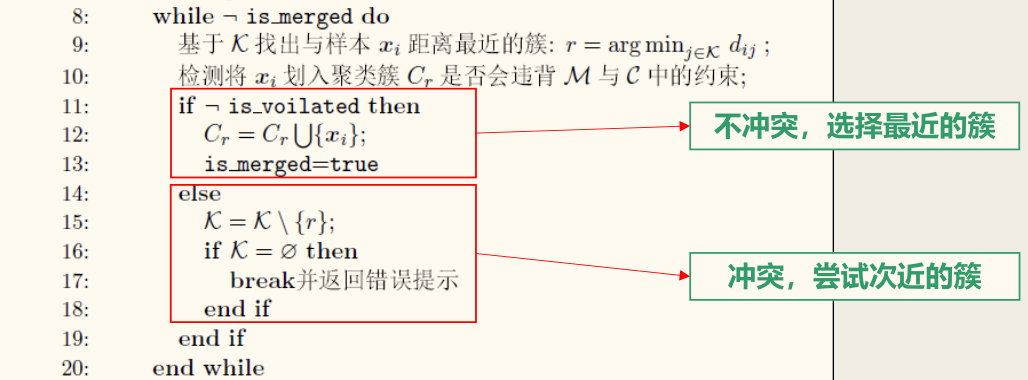
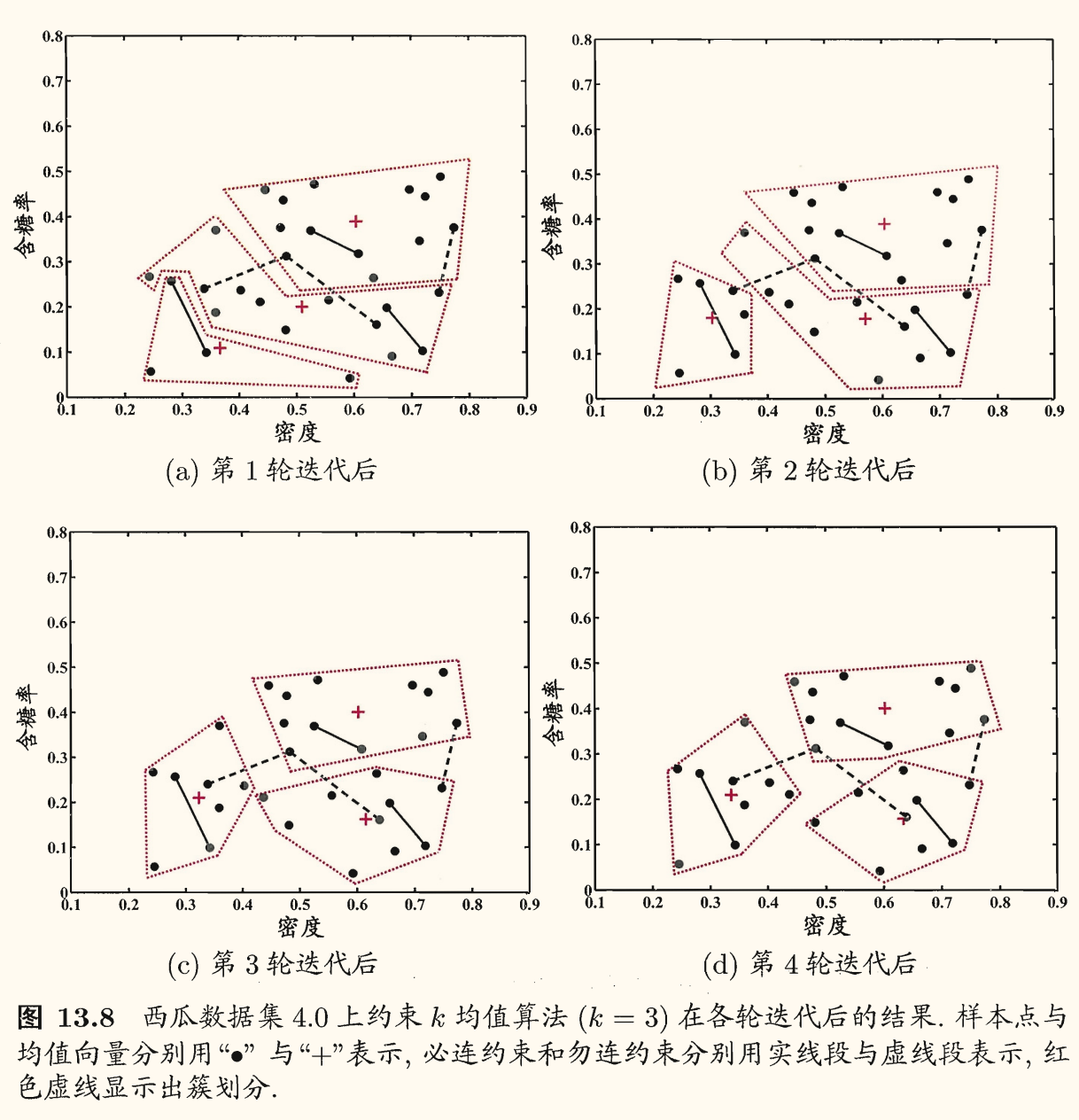
「约束 k k k k k k
算法如下:
例子:
第二类
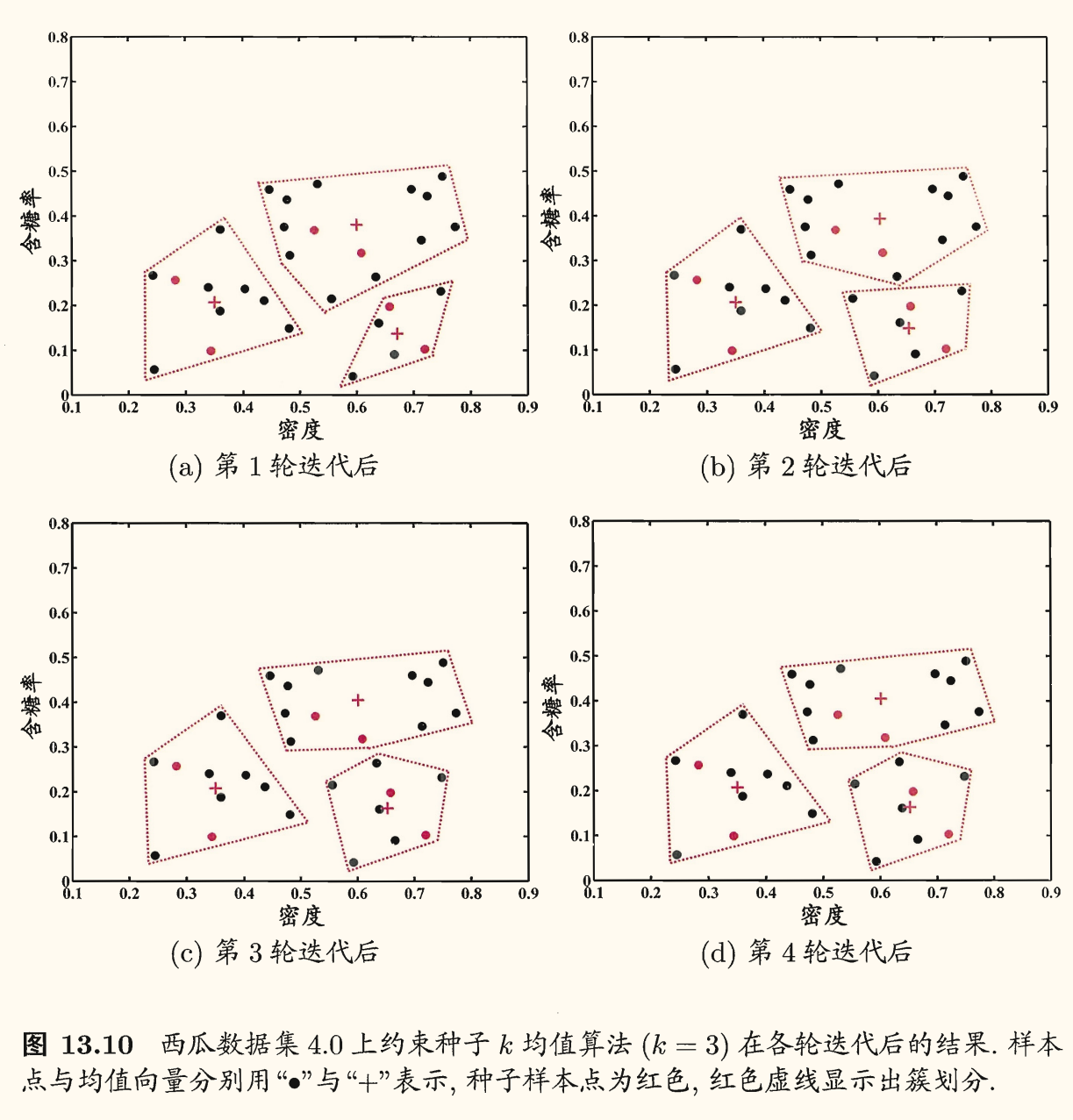
第二类监督信息是少量的有标记样本,即假设少量有标记样本属于 k k k
这样的监督信息利用起来很容易:直接将它们作为种子 ,用它们初始化 k k k k k k k k k
算法如下:
例子: