随机过程

随机过程

随机过程

一个随机过程（random/stochastic process）是一个随机变量的集合 $\left\lbrace X_t\colon t \in \mathscr{T} \right\rbrace$。

其中 $\mathscr{T}$ 是一个指标集（set of indices），通常视为时间（time）：

• 离散时间：$\mathscr{T}$ 可数，常用 $\mathbb{N}$ 或 $\mathbb{Z}_{+}$；
• 连续时间：$\mathscr{T}$ 不可数，常用 $[0, \infty )$。

$X_t$ 在状态空间 $\mathscr{S}$ 中取值：

• 离散空间：$\mathscr{S}$ 可数；
• 连续空间：$\mathscr{S}$ 不可数。

例子：

• 伯努利过程（Bernoulli process）：伯努利试验 $X_0, X_1, \dots, X_n \in \left\lbrace 0, 1 \right\rbrace$；
• 随机树过程（Branching (Galton-Watson) process）：$X_0 = 1,\, X_{n+1} = \displaystyle \sum_{j=1}^{X_n}\xi_{j}^{(n)}$，其中 $\left\lbrace \xi_{j}^{(n)}\colon n, j \ge 0\right\rbrace$ 是 i.i.d. 自然数值随机变量；
• 泊松过程（Poisson process）：连续时间过程 $\left\lbrace N(t) \mid t \ge 0 \right\rbrace$ 使得 $N(t) = \max\left\lbrace n \mid X_1, \dots, X_n \le t\right\rbrace$，其中 $\left\lbrace X_i \right\rbrace$ 是指数随机变量，参数 $\lambda > 0$。

鞅

从上一节笔记复制过来，以看的时候不用两边跑。

亏损加仓投注赌博策略也称为「鞅」（Martingale）策略。

定义

鞅

鞅是一个随机过程，其条件期望是给定过去所有信息的期望。

令 $\left\lbrace X_n \colon n \ge 0 \right\rbrace$ 是一个随机过程，若 $\left\lbrace Y_n\colon n \ge 0 \right\rbrace$ 对任意 $n$ 有「鞅性质」（martingale property）：

$$\boxed{\mathbb{E}[Y_{n+1} \mid X_0, X_1, \dots, X_n] = Y_n}$$

且 $\mathbb{E}[|Y_n|] < \infty$，则称序列 $\left\lbrace Y_n\colon n \ge 0 \right\rbrace$ 是一个鞅（martingale）。

根据定义，$Y_n$ 是 $X_0, X_1, \dots, X_n$ 的函数。

鞅是一个公平的过程，因为在任意时刻 $n$，$Y_n$ 的期望等于 $Y_{n-1}$ 的期望。另有：

• 上鞅（super-martingale）：$\mathbb{E}[Y_{n+1} \mid X_1, \dots, X_n] \le Y_n$
• 下鞅（sub-martingale）：$\mathbb{E}[Y_{n+1} \mid X_1, \dots, X_n] \ge Y_n$

$\left\lbrace X_n\colon n \ge 0 \right\rbrace$ 定义在概率空间 $(\Omega, \Sigma, \Pr)$ 上，有：

• $(X_0, X_1, \dots, X_n)$ 定义了一个子 $\sigma$-代数 $\Sigma_n \subseteq \Sigma$；
  • 也是最小的使得 $(X_0, \dots, X_n)$ 是 $\Sigma_n$ 可测的 $\sigma$-代数。
• $\left\lbrace \Sigma_n\colon n\ge 0 \right\rbrace$ 是 $\Sigma$ 的一个过滤（filtration），即 $\Sigma_0 \subseteq \Sigma_1 \subseteq \dots \subseteq \Sigma$；
• 鞅性质可表示为 $\mathbb{E}[Y_{n+1} \mid \Sigma_n] = Y_n$。

随着 $n$ 的增大，$\Sigma_n$ 表示越来越多的已知信息。$\Sigma_n$ 包含了从 $t = 0$ 到 $t = n$ 的所有信息。

例子

• Doob 鞅
• 公平赌博游戏
• 公平一维随机游走（unbiased 1D random walk）
• 棣莫弗鞅
• Polya 的瓮：瓮有不同颜色的弹珠，每轮均匀随机选择一个弹珠，然后换成 $k$ 个相同颜色的弹珠。

研究

• 鞅的测度集中（尾不等式）：在什么情况下有 $\Pr(|Yn - Y_0| \ge t) \le \mathord{?}$。
• 可选停止定理（OST, optional stopping theorem original sound track）：在什么情况下对于一个停止时 $\tau$ 有 $\mathbb{E}[Y_{\tau}] = \mathbb{E}[Y_0]$。

鞅尾不等式

吾妻不等式（Azuma's inequality）

若序列 $\left\lbrace Y_n\colon n \ge 0 \right\rbrace$ 是对某个序列 $\left\lbrace X_n\colon n \ge 0 \right\rbrace$ 的一个鞅，且对任意 $n \ge 1$ 有

$$|Y_n - Y_{n-1}| \le c_n$$

则对任意 $n \ge 1$ 与 $t > 0$ 有

$$\boxed{\Pr\left( |Y_n - Y_0| \ge t \right) \le 2 \exp\left(-\dfrac{2t^2}{\sum_{i=1}^{n}c_i^2}\right)}$$

该不等式以日本数学家「吾妻一兴」（Azuma Kazuoki）命名。

证明

差分 $D_i = Y_i - Y_{i-1}$ 与和 $S_n = \displaystyle \sum_{i=1}^{n}D_i = Y_n - Y_0$，则目标是证明

$$\Pr\left( |S_n| \ge t \right) \le 2 \exp\left( - \dfrac{2t^2}{\sum_{i=1}^{n}c_i^2} \right)$$

$\left\lbrace Y_n\colon n \ge 0 \right\rbrace$ 是鞅 w.r.t. $\left\lbrace X_n\colon n \ge 0 \right\rbrace$，则有

$$\begin{aligned} \mathbb{E}[D_n \mid X_0, \dots, X_{n-1}] &= \mathbb{E}[Y_n - Y_{n-1} \mid X_0, \dots, X_{n-1}]\\ &= \mathbb{E}[Y_n \mid X_0, \dots, X_{n-1}] - \mathbb{E}[Y_{n-1} \mid X_0, \dots, X_{n-1}]\\ &= Y_{n-1} - Y_{n-1}\\ &= 0 \end{aligned}$$

由于 $D_i$ 是有界的，则

$$\begin{aligned} D_n = Y_n - Y_{n-1}\in [-a_n, b_n] \end{aligned}$$

其中 $b_n - a_n = c_n$。

霍夫丁引理有，因为 $\mathbb{E}[D_n \mid X_0, \dots, X_{n-1}] = 0$ 与 $D_n \in [-a_n, b_n]$ 对于 $b_n - a_n = c_n$，则有

$$\mathbb{E}[\e^{\lambda D_n} \mid X_0, \dots, X_{n-1}] \le \e^{\lambda^2c_n^2/8}$$

而

$$\begin{aligned} \textcolor{ff0099}{\mathbb{E}[\e^{\lambda S_n}]} &= \mathbb{E}[\mathbb{E}[e^{\lambda S_n} \mid X_0, \dots, X_{n-1}]]\\ &= \mathbb{E}[\mathbb{E}[\e^{\lambda(S_{n-1}+D_n)} \mid X_0, \dots, X_{n-1}]]\\ &= \mathbb{E}[\e^{\lambda S_{n-1}}\mathbb{E}[\e^{\lambda D_n} \mid X_0, \dots, X_{n-1}]]\\ &\le \mathbb{E}[\e^{\lambda S_{n-1}}\e^{\lambda^2c_n^2/8}]\\ &= \e^{\lambda^2 c_n^2 / 8} \textcolor{ff0099}{\mathbb{E}[\e^{\lambda S_{n-1}}]} \end{aligned}$$

从而得

$$\mathbb{E}[\e^{\lambda S_n}] \le \exp\left( \dfrac{\lambda^2}{8}\sum_{i=1}^{n}c_i^2 \right)$$

上尾

$$\begin{aligned} \Pr(Y_n - Y_0 \ge t) &= \Pr(S_n \ge t)\\ &\le \Pr(\e^{\lambda S_n} \ge \e^{\lambda t})\\ &\le \e^{-\lambda t} \mathbb{E}[\e^{\lambda S_n}] &\text{(Markov 不等式)}\\ &\le \exp\left( -\lambda t + \dfrac{\lambda^2}{8}\sum_{i=1}^{n}c_i^2 \right)\\ &= \exp\left( -\dfrac{2t^2}{\sum_{i=1}^{n}c_i^2} \right) &\left(\lambda = \dfrac{4t}{\sum_{i=1}^{n}c_i^2}\right) \end{aligned}$$

下尾（类似，不过 $\lambda < 0$）

$$\begin{aligned} \Pr(Y_n - Y_0 \le -t) &= \Pr(S_n \le -t)\\ &\le \Pr(\e^{-\lambda S_n} \ge \e^{-\lambda t})\\ &\le \e^{\lambda t} \mathbb{E}[\e^{-\lambda S_n}] &\text{(Markov 不等式)}\\ &\le \exp\left( \lambda t + \dfrac{\lambda^2}{8}\sum_{i=1}^{n}c_i^2 \right)\\ &= \exp\left( -\dfrac{2t^2}{\sum_{i=1}^{n}c_i^2} \right) &\left(\lambda = -\dfrac{4t}{\sum_{i=1}^{n}c_i^2}\right) \end{aligned}$$

Doob 序列与吾妻不等式可得到 McDiarmid 不等式：

若随机向量 $\mathbf{X} = (X_1, \dots, X_n)$ 的函数 $f(\mathbf{X})$ 满足平均情况差分有界性质（average-case bounded differences property）：

$$\left\lvert \mathbb{E}\left[ f(\mathbf{X}) \mid X_1, \dots, X_i \right] - \mathbb{E}\left[ f(\mathbf{X} \mid X_1, \dots, X_{i-1}) \right] \right\rvert \le c_i$$

则有对任意 $t > 0$ 有

$$\Pr\left( \left\lvert f(\mathbf{X}) - \mathbb{E}[f(\mathbf{X})] \right\rvert \ge t \right) \le 2 \exp\left(-\dfrac{2t^2}{\sum_{i=1}^{n}c_i^2}\right)$$

若 $X_i \in \mathscr{X}_i$ 相互独立，且 $f\colon \mathscr{X}_1, \dots, \mathscr{X}_n \to\R$ 满足有界差分性质，那么 $f(\mathbf{X})$ 满足平均情况差分有界性质，从而有 McDiarmid 不等式。

随机图

图参数（graph parameter）$f(G)$ 可以是：上色数、团数等。

边 exposure 鞅是

$$Y_i = \mathbb{E}[f(G) \mid X_1, \dots, X_i],\quad 1 \le i \le \dbinom{n}{2}$$

其中 $X_1, \dots, X_{\binom{n}{2}}$ 是以 $p$ 为参数的 i.i.d. 伯努利随机变量，使得 $X_i$ 是第 $i$ 条边是否在图中的指示随机变量。

点 exposure 鞅是

$$Y_i = \mathbb{E}[f(G) \mid X_1, \dots, X_i],\quad 1 \le i \le n$$

其中 $X_i = G[\left\lbrace 1, \dots, i \right\rbrace]$ 是 $G$ 的一个从开始 $i$ 个顶点诱导出来的子图。

上色数（chromatic number）$\chi(G)$ 是最小的颜色数去涂色 $G$ 的顶点，使得相邻的顶点颜色不同。

任意顶点都可以指定一个新的颜色，即 $|Y_i - Y_{i-1}| \le 1$，于是吾妻不等式有

$$\Pr\left( \left\lvert \chi(G) - \mathbb{E}[\chi(G)] \right\rvert \ge \sqrt{c n} \right) \le 2 \e^{-2c}$$

公平赌博游戏

若 $\left\lbrace Y_n\colon n \ge 0 \right\rbrace$ 是鞅，则

$$\mathbb{E}[Y_n] = \mathbb{E}[Y_0]$$

证明

全期望有

$$\begin{aligned} \mathbb{E}[Y_n] &= \mathbb{E}[\mathbb{E}[Y_n \mid X_0, X_1, \dots, X_{n-1}]]\\ &= \mathbb{E}[Y_{n-1}] \end{aligned}$$

停止时间

序列 $\left\lbrace X_t\colon t \in \N \right\rbrace$ 的停止时间（stopping time）是一个自然数值随机变量 $T$ 使得对于任意 $n \ge 0$，$T = n$ 时的事件由 $X_0, X_1, \dots, X_n$ 确定。

形式化来说，$\left\lbrace X_t\colon t \in \N \right\rbrace$ 定义了一个 $\sigma$-代数的过滤 $\Sigma_0 \subseteq \Sigma_1 \subseteq \dots$ 使得 $(X_0, X_1, \dots, X_n)$ 是 $\Sigma_n$ 可测的。于是 $T$ 是一个停止时间，若 $\left\lbrace T = n \right\rbrace \in \Sigma_n$ 对任意 $n \ge 0$。

即 $T$ 是一个停止时间，若是否在 $n$ 时停止是由 $X_0, X_1, \dots, X_n$ 确定的。

停止的鞅

考虑鞅 $\left\lbrace Y_n\colon n \ge 0 \right\rbrace$ 与停止时间 $T$，停止的鞅（stopped martingale） $\left\lbrace Y_n^T\colon n\ge 0 \right\rbrace$ 定义为

$$Y_n^T = \begin{cases} Y_n, & n \le T\\ Y_T, & n > T \end{cases}$$

停止的鞅也是鞅。

证明

注意到事件 $T \ge i$ 由 $X_0, \dots, X_{i-1}$ 唯一确定，同时有

$$Y_i^T = Y_{i-1}^T + \mathbb{I}(T \ge i) \cdot (Y_i - Y_{i-1})$$

于是有

$$\begin{aligned} \mathbb{E}[Y_{i+1}^T \mid X_0, \dots, X_i] &= \mathbb{E}[Y_i^T + \mathbb{I}(T > i) \cdot (Y_{i+1} - Y_i) \mid X_0, \dots, X_i] \\ &= \mathbb{E}[Y_i^T \mid X_0, \dots, X_i] + \mathbb{E}[\mathbb{I}(T > i) \cdot (Y_{i+1} - Y_i) \mid X_0, \dots, X_i] \\ &= Y_i^T + \mathbb{I}(T > i) \cdot (\mathbb{E}[Y_{i+1} \mid X_0, \dots, X_i] - Y_i) \\ &= Y_i^T + \mathbb{I}(T > i) \cdot (Y_i - Y_i) \\ &= Y_i^T \end{aligned}$$

于是 $Y_n^T$ 是一个鞅。

Optional Stopping Theorem (OST)

若 $\left\lbrace Y_n\colon n \ge 0 \right\rbrace$ 是鞅，$T$ 是停止时间，则有

$$\mathbb{E}[Y_T] = \mathbb{E}[Y_0]$$

当下列其一成立时：

• 有界时间：存在有限的 $n$ 使得 $T < n$；
• 有界范围：$T < \infty$ 几乎必然成立，同时存在有限的 $c$ 使得对于任意 $t \le T$ 使得 $\left| Y_t \right| \le c$；
• 有界差分：$\mathbb{E}[T] < \infty$，同时存在有限的 $c$ 使得对任意 $t \ge 0$ 有 $\mathbb{E}[|Y_{t+1} - Y_t| \mid X_{\le t}] < c$。

一般条件（general condition），即下面所有条件成立：

1. $\Pr(T < \infty ) = 1$；
2. $\mathbb{E}[|Y_T|] < \infty$；
3. $\lim\limits_{n\to \infty }\mathbb{E}[Y_n \cdot I[Y > n]] = 0$。

证明

对于第一个条件，即存在有限的 $n$ 使得 $T < n$。则有 $n \le T \le m$。则有更强的等式

$$\mathbb{E}[Y_T \mid X_0, \dots, X_{n-1}] = Y_n$$

证明如下：

$$\begin{aligned} \mathbb{E}[Y_T \mid X_{<n}] &= \mathbb{E}\left[ \mathbb{E}[Y_T \mid X_{<m}] \mid X_{<n} \right] \\ &= \mathbb{E}\left[ \sum_{k \in [n, m]}\mathbb{E}[Y_{k} \cdot \mathbb{I}(T = k) \Biggm| X_{<m}] \mid X_{<n} \right] \\ &= \mathbb{E}\left[ \sum_{k \in [n, m)}Y_{k} \cdot \mathbb{I}(T = k)\Biggm| X_{<n} \right] + \mathbb{E}\left[\mathbb{E}\left[Y_m \cdot \mathbb{I}(T = m) \mid X_{<m}\right] \mid X_{<n}\right] \\ &= \mathbb{E}\left[ \sum_{k \in [n, m)}Y_{k} \cdot \mathbb{I}(T = k)\Biggm| X_{<n} \right] + \mathbb{E}\left[\mathbb{E}[Y_m \mid X_{< m}] \cdot \mathbb{I}(T = m) \mid X_{<n}\right] \\ &= \mathbb{E}\left[ \sum_{k \in [n, m)}Y_{k} \cdot \mathbb{I}(T = k)\Biggm| X_{<n} \right] + \mathbb{E}\left[Y_{m-1} \cdot \mathbb{I}(T = m) \mid X_{<n}\right] \\ &= \mathbb{E}[Y_{\min\left\lbrace T, m-1 \right\rbrace} \mid X_{<n}] \\ &= \cdots\\ &= \mathbb{E}[Y_{\min\left\lbrace T, n \right\rbrace} \mid X_{<n}] \\ &= \mathbb{E}[Y_n \mid X_{<n}]\\ &= Y_n \end{aligned}$$

---

对于第二个条件，$\Pr(T < \infty ) = 1$ 且 $\mathbb{E}\left[ \max_t |Y_t| \right] < \infty$ 对于任意 $t \le T$ 成立，于是

$$\mathbb{E}[Y_T] = Y_0$$

证明如下：

可以（不太严格地）证明

$$\lim\limits_{n \to \infty} \left\lvert \mathbb{E}\left[ Y_{\min\left\lbrace T_n \right\rbrace} \right] - \mathbb{E}[Y_T] \right\rvert = 0$$

因此 $\mathbb{E}[Y_T] = \lim\limits_{n \to \infty} \mathbb{E}[Y_{\min\left\lbrace T, n \right\rbrace}]$。

令 $T' = \min\left\lbrace T, n \right\rbrace$，于是有 $T' \in [0, n]$，于是由第一个条件（有界时间的情况）可得 $\mathbb{E}[Y_{T'}] = Y_0$。

从而有 $\mathbb{E}[Y_T] = Y_0$。

而 $\lim\limits_{n \to \infty} \left\lvert \mathbb{E}\left[ Y_{\min\left\lbrace T_n \right\rbrace} \right] - \mathbb{E}[Y_T] \right\rvert = 0$ 的证明如下：

令 $W = \max_t |Y_{\min\left\lbrace T, t \right\rbrace}$。根据假设有 $\mathbb{E}[|Y_T|] \le \mathbb{E}[W] < \infty$。则

$$\begin{aligned} \left\lvert \mathbb{E}\left[ Y_{\min\left\lbrace T, n \right\rbrace} - \mathbb{E}[Y_T] \right] \right\rvert &\le \mathbb{E}\left[ \left\lvert Y_{\min\left\lbrace T, n \right\rbrace} - Y_T \right\rvert \mid \mathbb{I}(T \ge n)\right] \\ &\le 2 \mathbb{E}[W \cdot \mathbb{I}(T \ge n)] \end{aligned}$$

而 $\Pr(T < \infty ) = 1$，$\mathbb{E}[W] < \infty$，于是

$$\lim\limits_{n \to \infty} 2 \mathbb{E}[W \cdot \mathbb{I}(T \ge n)] = 0$$

从而有

$$\lim\limits_{n \to \infty} \left\lvert \mathbb{E}\left[ Y_{\min\left\lbrace T, n \right\rbrace} - \mathbb{E}[Y_T] \right] \right\rvert = 0$$

---

对于第三个条件，$\mathbb{E}[T] < \infty$ 且存在有限的 $c$ 使得对任意 $t \ge 0$ 有 $\mathbb{E}[|Y_{t+1} - Y_t| \mid X_{\le t}] < c$。加上 $\Pr(T < \infty ) = 1$，有

$$\mathbb{E}[Y_T] = Y_0$$

证明如下：

令 $Z_n = |Y_n - Y_{n-1}|$，且 $Z_0 = |Y_0|$，与 $W = Z_0 + \dots + Z_T$。显然 $W \ge |Y_T|$。

则

$$\begin{aligned} \mathbb{E}[W] &= \sum_{k\ge 0}\mathbb{E}[Z_{k} \cdot \mathbb{I}(T \ge k)]\\ &= \sum_{k\ge 0}\mathbb{E}[\mathbb{E}[Z_{k} \cdot \mathbb{I}(T \ge k) \mid X_{< k}]]\\ &= \sum_{k\ge 0}\mathbb{E}\left[ \mathbb{I}(T \ge k) \cdot \mathbb{E}[|Y_{k} - Y_{k-1}| \mid X_{<k}] \right] \\ &\le \sum_{k\ge 0} c \cdot \Pr(T \ge k)\\ &\le c (1 + \mathbb{E}[T])\\ &< \infty \end{aligned}$$

一维对称随机游走

令 $Y_t = \sum_{i=1}^{t}X_i$，其中 $X_i \in \left\lbrace -1, 1 \right\rbrace$ 是 i.i.d. 均匀随机变量。令 $T$ 表示第一个使得 $Y_t = -a$ 或 $Y_t = b$ 的时间 $t$。

则 $\left\lbrace Y_t \colon t \ge 0 \right\rbrace$ 是鞅，且 $T$ 是停止时间，关于 $\left\lbrace X_i \colon i \ge 1 \right\rbrace$。

其满足 $|Y_t| \le \max\left\lbrace a, b \right\rbrace$ 对任意 $0 \le t \le T$，同时 $T < \infty$ 几乎必然成立。于是 OST 可以应用于该过程，即 $\mathbb{E}[Y_T] = \mathbb{E}[Y_0] = 0$。

有

$$\mathbb{E}[Y_T] = b \Pr(Y_T = b) - a \Pr(Y_T \ne b) = 0$$

因此 $\Pr(Y_T = b) = \dfrac{a}{a+b}$。

Wald 等式

Wald's equation

若 $\left\lbrace X_i \right\rbrace$ 是 i.i.d. 随机变量，且 $\mu = \mathbb{E}[X_i] < \infty$，$T$ 是关于 $\left\lbrace X_i \right\rbrace$ 的停止时间。若 $\mathbb{E}[T] < \infty$，于是

$$\mathbb{E}\left[ \sum_{i=1}^{T}X_i \right] = \mu \mathbb{E}[T]$$

证明

对于 $t \ge 1$，令 $Y_t = \sum_{i=1}^{t} (X_i - \mu)$，则 $Y_t$ 是一个鞅。

注意到 $\mathbb{E}[T] < \infty$ 且 $\mathbb{E}[|Y_{t+1} - Y_t| \mid X_1, \dots, X_t] = \mathbb{E}[|X_{t+1} - \mu|] < \infty$，于是 OST 可以应用于该过程，即

$$\mathbb{E}[Y_T] = \mathbb{E}\left[ \sum_{i=1}^{T} X_i \right] - \mu \mathbb{E}[T]$$

故

$$\mathbb{E}\left[ \sum_{i=1}^{T} X_i \right] = \mu \mathbb{E}[T]$$

马尔可夫链

定义

马尔可夫链（Markov chain）

一个离散时间随机过程 $\left\lbrace X_0, X_1, \dots \right\rbrace$ 是一个马尔可夫链（Markov chain）若

$$\Pr(X_{t+1} = x_{t+1} \mid X_t = x_t, \dots, X_0 = x_0) = \Pr(X_{t+1} = x_{t+1} \mid X_t = x_t)$$

即给定当前状态，未来状态的条件概率只与当前状态有关。

马尔可夫性质（无记忆性）：

• 下一个状态 $X_{t+1}$ 只与当前状态 $X_t$ 有关，与如何到达 $X_t$ 的历史 $X_{t-1}, X_{t-2}, \dots, X_0$ 独立；
• $X_{t+1}$ 在给定 $X_t$ 的条件下，（条件）独立于 $X_0, X_1, \dots, X_{t-1}$。

转移矩阵（Transition Matrix）

离散随机过程 $X_0, X_1, \dots$ 是马尔可夫链，有

$$\begin{aligned} \Pr(X_{t+1} = x_{t+1} \mid X_t = x_t, \dots, X_0 = x_0) &= \Pr(X_{t+1} = x_{t+1} \mid X_t = x_t)\\ &= P(x_t, x_{t+1})\\ &= \mathbf{P}^{(t)}(x_t, x_{t+1}) \end{aligned}$$

这称为 Time Homogeneous（时间同质性）。

于是 $\mathbf{P}$ 称为转移矩阵（transition matrix），其中

$$\mathbf{P}(x, y) = \Pr(X_{t+1} = y \mid X_t = x)$$

对任意 $x, y \in \mathscr{S}$ 成立，其中 $\mathscr{S}$ 是 $X_0, X_1, \dots$ 取值的离散状态空间。

$\mathbf{P}$ 是一个（行/右）随机矩阵（stochastic matrix^[1]），有 $\mathbf{P} \ge 0$ 与 $\mathbf{P} \bm{1} = \bm{1}$，即每一行元素非负且和为 1。

---

1. 矩阵元素随机取值的矩阵称为 random matrix。stochastic matrix 专指马尔可夫转移矩阵。 ↩︎

转移矩阵「每行」代表「一个当前状态」，「每列」代表「每个下一个状态」。因此每行和为 1。

令 $\bm{\pi}^{(t)}(x) = \Pr(X_t = x)$ 是 $X_t$ 的 pmf^[1]，全概率有

$$\begin{aligned} \bm{\pi}^{(t+1)}(y) &= \Pr(X_{t+1} = y)\\ &= \sum_{x \in \mathscr{S}}\Pr(X_{t+1} = y \mid X_t = x) \cdot \Pr(X_t = x)\\ &= (\bm{\pi}^{(t)}\mathbf{P})_y \end{aligned}$$

即 $\bm{\pi}^{(t+1)} = \bm{\pi}^{(t)}\mathbf{P}$：

$$\bm{\pi}^{(0)} \xrightarrow[]{\mathbf{P}} \bm{\pi}^{(1)} \xrightarrow[]{\mathbf{P}} \dots \xrightarrow[]{\mathbf{P}} \bm{\pi}^{(t)} \xrightarrow[]{\mathbf{P}} \bm{\pi}^{(t+1)} \xrightarrow[]{\mathbf{P}} \dots$$

从而有上面的

$$\bm{\pi}^{(t)} = \bm{\pi}^{(0)}\mathbf{P}^t$$

稳态分布

稳态分布（Stationary Distribution）

状态空间 $\mathscr{S}$ 上的分布（pmf）$\bm{\pi}$ 称为马尔可夫链 $\mathbf{P}$ 的稳态分布（stationary distribution, 平稳分布），若

$$\bm{\pi} \mathbf{P} = \bm{\pi}$$

$\bm{\pi}$ 是一个线性动态系统（linear dynamic system）的不动点（fixpoint, equilibrium）。

即 $1$ 是 $\mathbf{P}$ 的一个特征值，对应的特征向量即为 $\bm{\pi}$。

稳态分布一定存在，但不一定唯一，且不一定收敛。

如下图，状态 $A, B$ 总会保持状态不变。稳态分布 $\bm{\pi} = \lambda \bm{\pi}_A + (1-\lambda) \bm{\pi}_B$，$\lambda$ 可以是 $[0, 1]$ 中的任意值。即稳态分布不唯一。

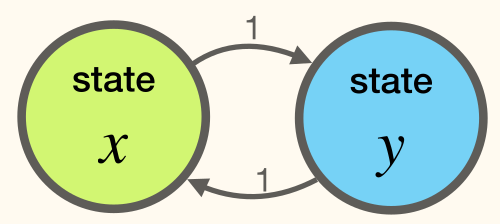
再如下图，状态总是会从 $x$ 转移到 $y$，再从 $y$ 转移回 $x$，转移矩阵为 $\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$。稳态分布不收敛。

下面讨论马尔可夫链的收敛定理。

• 不可约性（irreducible）：马尔可夫链是不可约的（irreducible, 可达的），若转移矩阵 $\mathbf{P}$ 是不可约矩阵（irreducible matrix）；
  • 即状态空间 $\mathscr{S}$ 在 $\mathbf{P}$ 下是强连通（strongly connected）的。
• 无周期性（aperiodic）：马尔可夫链是遍历（ergodic）的，若所有状态都无周期（aperiodic），且正常返（positive recurrent）。

状态 $x \in \mathscr{S}$ 的周期（period）$d(x)$ 定义为

$$d(x) = \gcd\left\lbrace t \ge 1 \mid \mathbf{P}^{(t)}(x, x) > 0 \right\rbrace$$

若 $d(x) = 1$，则称 状态 $x \in \mathscr{S}$ 称为「非周期性」（aperiodic）的。若 $d(x) > 1$，则称为「周期性」（periodic）的。

$\mathbf{P}(x, x) > 0$ 能推出 $x$ 是非周期性的。因为存在一步返回的情况，这时候返回时间的最大公约数是 1（实际上直接因为 $\mathbf{P}^{(1)} \in \left\lbrace t \ge 1 \mid \mathbf{P}^{(t)}(x, x) > 0 \right\rbrace$ 就能得出了）。

一个状态 $x \in \mathscr{S}$ 称为常返（reccurent）的，若

$$\Pr(\exists t \ge 1, X_t = x \mid X_0 = x) = 1$$

即从 $x$ 出发，几乎必然会回到 $x$。

更进一步，称为是正常返（positive recurrent）的，若

$$\mathbb{E}[\min\left\lbrace t \ge 1 \mid X_t = x \mid X_0 = x \right\rbrace] < \infty$$

即从 $x$ 出发，平均回到 $x$ 的时间是有限的。

在有限状态空间 $\mathscr{S}$ 上，不可约可以推出任意状态都是正常返的。

马尔可夫链收敛定理（Convergence Theorem）

若马尔可夫链是不可约的（irreducible, 可达的）且无周期性（aperiodic, 遍历的）的，则存在唯一的 $\mathscr{S}$ 上的稳态分布 $\bm{\pi}$ 使得

$$\bm{\pi}(x) = \lim_{t \to \infty } \Pr(X_t = x \mid X_0 = x_0)$$

对任意 $x_0 \in \mathscr{S}$ 成立。

马尔可夫链的基本定理（Fundamental Theorem of MC）。
充分条件而非必要条件。

性质：

• Perron-Frobenius 定理
  • 有限性（finitiness）$\implies$ 存在性（existence）
  • 不可约性（irreduciblity）$\implies$ 唯一性（uniqueness）
• 遍历性（ergodicity）$\implies$ 收敛性（convergence）

证明

PageRank

PageRank 是 Google 的搜索引擎排序算法。

任意一个网页 $x \in \mathscr{S}$ 赋以一个权重 $r(x)$：

• 高权页有更强的影响；
• 若一个高权页指向 $x$，则 $x$ 也有高权。
• 指向较少的页影响更强。

线性系统

$$r(x) = \sum_{y \to x} \dfrac{r(y)}{d^{+}(y)}$$

其中 $d^{+}(y)$ 是 $y$ 的出度。

解上面的方程比较复杂，可以转化为马尔可夫链的问题。

对于一个随机游走的稳态分布 $\mathbf{r} \mathbf{P} = \mathbf{r}$，有

$$\mathbf{P}(x, y) = \begin{cases} \dfrac{1}{d^{+}(y)}, & x \to y\\ 0, & \text{otherwise} \end{cases}$$

时间可逆性（Time Reversibility）

马尔可夫链称为时间可逆（time reversible）或可逆（reversible），若其对于状态空间 $\mathscr{S}$ 上的某些分布 $\bm{\pi}$，满足细致平衡条件（detailed balance condition, DBE），即

$$\bm{\pi}(x)\mathbf{P}(x, y) = \bm{\pi}(y)\mathbf{P}(y, x)$$

这样的 $\bm{\pi}$ 是一个更好（refined）的不动点，$\bm{\pi}$ 一定是一个稳态分布因为有

$$(\bm{\pi} \mathbf{P})_y = \sum_x \bm{\pi}(x)\mathbf{P}(x, y) = \sum_x \bm{\pi}(y)\mathbf{P}(y, x) = \bm{\pi}(y)$$

时间可逆：假设 $X_0 \sim \bm{\pi}$，则 $(X_0, X_1, \dots, X_n)$ 与 $(X_n, \dots, X_1, X_0)$ 同分布。

收敛定理

有限马尔可夫链（有限状态空间 $\mathscr{S}$ 上）：惰性（lazy, i.e. $\mathbf{P}(x, x) > 0$）与强连接（strongly connected）马尔可夫链 $\mathbf{P}$ 可以推出，其总是收敛到唯一的稳态分布 $\bm{\pi} = \bm{\pi} \mathbf{P}$。

马尔可夫链的收敛速度

混合时间（Mixing time）：令 $\bm{\pi}^{(t)}_x(y) = (\bm{1}_x \mathbf{P}^t)_y = \Pr(X_t = y \mid X_0 = x)$^[2]，有

$$\tau(\epsilon) = \max_{x \in \mathscr{S}} \min\left\lbrace t \ge 1 \Bigm| \left\lVert \bm{\pi}_x^{(t)} - \bm{\pi} \right\rVert_1 \le 2\epsilon \right\rbrace$$

混合时间表示，从任意状态 $x$ 出发，经过 $\tau(\epsilon)$ 步后，分布 $\bm{\pi}_x^{(\tau(\epsilon))}$ 与稳态分布 $\bm{\pi}$ 的距离不会超过 $2\epsilon$。

其他随机过程

• 平稳过程：$\left\lbrace X_t \right\rbrace$ 的联合分布在时间平移下不变，即 $(X_{t_1}, X_{t_2}, \dots, X_{t_n})\sim(X_{t_1 + \tau}, X_{t_2 + \tau}, \dots, X_{t_n + \tau})$;
• Renewal 过程（counting processes, 计数过程）：$N(t) = \max\left\lbrace n \mid X_1 + \dots + X_n \le t \right\rbrace$，其中 $\left\lbrace X_i \right\rbrace$ 是 i.i.d. 非负值随机变量；
  • 泊松随机过程（唯一的是 Renewal 过程的马尔可夫链）。
• Wiener 过程（Brownian motion）：连续时间、连续空间 $\left\lbrace W(t) \in \R\colon t \ge 0 \right\rbrace$ 有着时间同质性（time homogeneity）与独立增量（independent increments）性质：
  • $W(s_i) - W(t_i)$ 相互独立对于任意互不相交的区间 $(s_i, t_i]$ 成立；
  • $W(s + u) - W(s) \sim \mathcal{N}(0, u)$；

扩散过程（Diffusion Processes）

令 $(\Omega, \Sigma, \Pr)$ 是一个概率空间，$X\colon \mathscr{T} \times \Omega \to \mathscr{S}$ 是以时间范围 $\mathscr{T}$ 与状态空间 $\mathscr{S}$ 的随机过程，其被称为扩散过程（diffusion process）若存在 $A \in \Sigma$ 使得 $\Pr(A) = 1$，使得对所有 $\omega \in A$ 有

$$X(\omega)\colon \mathscr{T} \to \mathscr{S}$$

是一个连续函数（在拓扑空间中，between topological spaces）。

Wiener 过程是一维扩散过程。

工具：伊藤微积分（Itô calculus）。

---

1. 这里的 $\bm{\pi}$ 是一个 $1 \times |\mathscr{S}|$ 的行向量，$\bm{\pi}(x)$ 即为第 $x$ 个状态的概率。 ↩︎

2. $\bm{\pi}_x^{(t)}(y)$ 表示从 $x$ 出发，$t$ 步后到达 $y$ 的概率。$\bm{1}_x$ 表示一个初始分布向量，即 $x$ 处为 1，其他地方为 0。 ↩︎