假设检验

• 问题：抽卡是否被暗改概率？
• 收集数据：抽卡记录

永远无法准确地判断，但可以量化我们的把握：

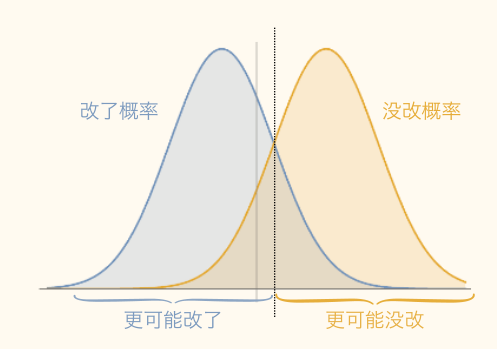
假设检验

概念

• 原假设（零假设，null hypothesis）
• 备择假设（alternative hypothesis）
• 检验法则（decision rule）：
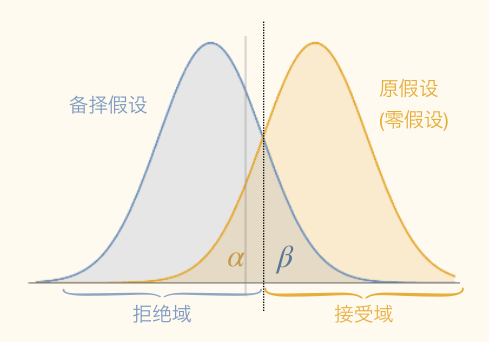
  • 接受域（acceptance region）：应该接受原假设
  • 拒绝域（rejection region）/临界域（critical region）：应该拒绝原假设

	接受原假设	拒绝原假设
原假设为真	正确（TP）	一类错误（弃真/假阳性 FP）
原假设为假	二类错误（取伪/假阴性 FN）	正确（TN）

一种假设检验基本步骤：

1. 提出统计假设：原假设 $H_0$ 和备择假设 $H_1$
2. 针对两种假设确定能区分它们的统计量
3. 根据统计量确定拒绝域和接受域
4. 采样，从样本中计算出统计值
5. 判断统计值是否在拒绝域内，做出决策

对这种方法，考虑边界情况、判断的可信度、出错率？

犯错概率，有

• 原假设为真，犯一类错误概率为 $\alpha$
  • 显著性（significance）：$\alpha$
  • 置信水平 $\gamma = 1-\alpha$
• 备择假设为真，犯二类错误概率为 $\beta$
  • 检验功效（power）：$1-\beta$

Fisher 显著性检验：

• 显著：$5\%$
• 极为显著：$1\%$

	接受原假设	拒绝原假设
原假设为真	$1-\alpha$	$\alpha$
原假设为假	$\beta$	$1-\beta$

生男生女

John Arbuthnot（1710）统计了 82 年间（1629 ~ 1710）伦敦出生的男女比例，均为男比女多。如果假设男女比例相等，那么这种情况发生的概率是 $\dfrac{1}{2^{82}}$。

改版女士品茶

某个吃货能否区分：

• 先吃一口夏洛特蛋糕，再吃一口便利店鸡排
• 先吃一口便利店鸡排，再吃一口夏洛特蛋糕

原假设是这两种吃法口味一样，备择假设是不一样。

• 试验：有四组实验，每组各有一份，让她在无感知情况下随机品尝，并从中选出一份先吃夏洛特蛋糕的。^[1]
• 数据：受试者对了 $k$ 次
• 原假设为真情况下样本出现的概率为 $\dbinom{4}{k} / \dbinom{8}{4}$。

原版女士品茶中，受试者藻类学家 Muriel Bristol 全对，概率为 $1 / \dbinom{8}{4} = \dfrac{1}{70} \approx 1.429\%$。

---

1. 改了例子后说明很拗口。换成可乐比较容易懂。就是有四杯可口和四杯百事，受试者随机品尝并从中选出四杯可口，数据是对了 $k$ 杯。不过本来就是私货，拗口也要放在主体。 ↩︎

由此添加了第三步「规定显著性水平 $\alpha$」。

假设检验基本步骤（Neyman-Pearson's approach）：

1. 提出统计假设：原假设 $H_0$ 和备择假设 $H_1$
2. 针对两种假设确定能区分它们的统计量
3. 规定显著性水平 $\alpha$
4. 根据统计量确定拒绝域和接受域
5. 采样，从样本中计算出统计值
6. 判断统计值是否在拒绝域内，做出决策：「在显著性水平 $\alpha$ 下接受/拒绝原假设」

$\alpha, \beta$ 互相矛盾（像是精确度 $P$ 和召回率 $R$）。

可以增大样本量，减小假设样本方差，假设样本更集中，重叠区域更小：

• 固定 $\alpha$，提高样本量使 $\beta \le \alpha$
• 样本量由 $\beta$ 确定（功耗）

正态总体参数检验

已知方差 $\sigma^2$，检验期望 $\mu$

例如一洗衣粉包装机，额定标准为 500g/包，袋装重量服从正态分布 $\mathcal{N}(\mu, \sigma^2)$，称得样本 $X_1, \dots, X_n$，取显著性水平 $\alpha$，包装机是否工作正常？

Z 检验

若样本 $X_1, \dots, X_n$ 服从正态分布 $\mathcal{N}(\mu, \sigma^2)$，取显著性水平 $\alpha$，则：

检验统计量 $\boxed{Z = \dfrac{\bar{X} - \mu_0}{\sigma / \sqrt{n}}}$，若原假设 $H_0\colon \mu = \mu_0$ 成立，则 $Z \sim \mathcal{N}(0, 1)$。

令 $X \sim \mathcal{N}(0, 1)$，有

• 备择假设 $H_1\colon \mu \ne \mu_0$（双侧检验）拒绝域

$$\left\lbrace z\colon \Pr(X \le z) \le \alpha / 2 \text{ or } \Pr(X \ge z) \le \alpha / 2 \right\rbrace$$

• 备择假设：$H_1\colon \mu < \mu_0$（左侧检验）拒绝域

$$\left\lbrace z\colon \Pr(X \le z) \le \alpha \right\rbrace$$

• 备择假设 $H_1\colon \mu > \mu_0$（右侧检验）拒绝域

$$\left\lbrace z\colon \Pr(X \ge z) \le \alpha \right\rbrace$$

$z_{\alpha}$ 表示使得 $\Pr(X \ge z_{\alpha}) = \alpha$ 的 $z$ 值，其中 $X \sim \mathcal{N}(0, 1)$。

已知期望 $\mu$，检验方差 $\sigma^2$

例如一洗衣粉包装机，额定标准为 500g/包，袋装重量服从正态分布 $\mathcal{N}(\mu, \sigma^2)$，称得样本 $X_1, \dots, X_n$，取显著性水平 $\alpha$，检验 $\sigma^2 = \sigma_0^2$。

卡方检验

若样本 $X_1, \dots, X_n$ 服从正态分布 $\mathcal{N}(\mu, \sigma^2)$，则：

样本方差 $S^2 = \dfrac{\sum_i (X_i - \bar{X})^2}{n - 1}$，有 $\mathbb{E}[S^2] = \sigma^2$。

检验统计量 $\boxed{Z = \dfrac{\sum_i(X_i - \mu)^2}{\sigma_0^2}}$，若原假设 $H_0\colon \sigma^2 = \sigma_0^2$，则 $Z \sim \chi^2(n)$。

令 $X \sim \chi^2(n)$，有

• 备择假设 $H_1\colon \sigma^2 \ne \sigma_0^2$（双侧检验）拒绝域

$$\left\lbrace z\colon \Pr(X \le z) \le \alpha / 2 \text{ or } \Pr(X \ge z) \le \alpha / 2 \right\rbrace$$

卡方分布

若 $X_1, \dots, X_n$ 独立同分布，且 $X_i \sim \mathcal{N}(0, 1)$，则 $Q = \sum_i X_i^2 \sim \chi^2(n)$，称 $Q$ 服从自由度为 $n$ 的卡方分布。

若 $Q \sim \chi^2(n)$，则有 $\mathbb{E}[Q] = n$。若 $X_1 \sim \chi^2(m), X_2 \sim \chi^2(n)$ 相互独立，则 $X_1 + X_2 \sim \chi^2(m + n)$。

未知期望 $\mu$，检验方差 $\sigma^2$

例如一洗衣粉包装机，额定标准为 500g/包，袋装重量服从正态分布 $\mathcal{N}(\mu, \sigma^2)$，称得样本 $X_1, \dots, X_n$，已知 $\mu = \mu_0$，取显著性水平 $\alpha$，检验 $\sigma^2 = \sigma_0^2$。

卡方检验

未知期望，检验统计量 $\boxed{Z = \dfrac{\sum_i (X_i - \bar{X})^2}{\sigma_0^2}}$，若原假设 $\sigma^2 = \sigma_0^2$ 成立，则 $Z \sim \chi^2(n-1)$。

证明

即证若 $X_1, \dots, X_n \sim \mathcal{N}(0, 1)$，则 $Z = \sum_i (X_i - \bar{X})^2 \sim \chi^2(n - 1)$。

样本方差 $S^2 = \displaystyle \sum_{i=1}^{n} \dfrac{(X_i - \bar{X})^2}{n - 1}$。

有 $\displaystyle \sum_{i=1}^{n} (X_i - \bar{X})^2 = \sum_{i=1}^{n} X_i^2 - n \bar{X}^2$，显然 $\displaystyle \sum_{i=1}^{n} X_i^2 \sim \chi^2(n)$。

又 $\bar{X} \sim \mathcal{N}\left(0, \frac{1}{n}\right)$，于是 $\sqrt{n}\bar{X} \sim \mathcal{N}(0, 1)$，且 $n \bar{X}^2 \sim \chi^2(1)$。

改写 $\displaystyle \sum_{i=1}^{n} X_i^2 = (n - 1)S^2 + n \bar{X}^2$，记作 $\chi^2(n) = (n - 1)S^2 + \chi^2(1)$，这两个是相互独立的（样本方差与样本均值相互独立）。

于是可以用 MGF 有

$$\begin{aligned} M_{\chi^2_n}(t) &= M_{(n-1)S^2 + \chi^2(1)}(t) \\ &= M_{(n-1)S^2}(t) \cdot M_{\chi^2(1)}(t) \\ \end{aligned}$$

而 $M_{\chi_n^2}(t) = (1 - 2t)^{-n / 2}$，则有

$$\begin{aligned} M_{(n - 1)S^2}(t) &= M_{\chi_n^2}(t) / M_{\chi^2(1)}(t) \\ &= (1 - 2t)^{-n / 2} \cdot (1 - 2t)^{1 / 2} \\ &= (1 - 2t)^{-(n - 1) / 2} \end{aligned}$$

因此 $\displaystyle \sum_{i=1}^{n} (X_i - \bar{X})^2 = (n - 1)S^2 \sim \chi^2(n - 1)$。

上面的证明还有两步未完成，即「样本方差与样本均值相互独立」和「MGF 的计算」，先看后者：

令 $X \sim \chi_n^2$，则其概率密度函数^[1]为

$$f(x) = \dfrac{x^{n / 2 - 1} \e^{-x / 2}}{2^{n / 2} \Gamma(n / 2)}$$

$$\Gamma(z) = \int_0^\infty t^{z - 1} \e^{-t} \d t$$

于是

$$\begin{aligned} M_X(t) &= \mathbb{E}[\exp(t X)]\\ &= \int_0^{\infty } \exp(t x) \cdot f(x) \d x\\ &= \dfrac{1}{2^{n / 2} \Gamma(n / 2)} \int_0^{\infty } x^{n / 2 - 1} \exp\left( - (1 / 2 - t) x \right) \d x\\ &= \dfrac{1}{2^{n / 2} \Gamma(n / 2)} \int_0^{\infty } \left( \dfrac{u}{1 / 2 - t} \right)^{n / 2 - 1} \dfrac{\e^{-u}}{1 / 2 - t} \d u & (u = (1 / 2 - t) x)\\ &= \dfrac{1}{2^{n / 2} \Gamma(n / 2) (1 / 2 - t)^{n / 2}} \int_0^{\infty } u^{n / 2 - 1} \e^{-u} \d u\\ &= \dfrac{1}{2^{n / 2} \Gamma(n / 2) (1 / 2 - t)^{n / 2}} \Gamma(n / 2)\\ &= (1 - 2t)^{-n / 2} \end{aligned}$$

另一个见下面。

令 $X \sim \chi^2(n-1)$，有

• 备择假设 $H_1\colon \sigma^2 \ne \sigma_0^2$（双侧检验）拒绝域

$$\left\lbrace z\colon \Pr(X \le z) \le \alpha / 2 \text{ or } \Pr(X \ge z) \le \alpha / 2 \right\rbrace$$

---

1. 那卡方分布 PDF 怎么来的呢？即答「PPT 是这样写的」，查表可得。那为啥 MGF 不查表呢？我只是个抄书的，我什么都不知道。 ↩︎

未知方差 $\sigma^2$，检验期望 $\mu$

t 检验

样本 $X_1, \dots, X_n$ 服从某正态分布 $\mathcal{N}(\mu, \sigma^2)$，方差 $\sigma^2$ 未知。取显著性水平 $\alpha$，检验 $\mu = \mu_0$：

• 原假设 $H_0\colon \mu = \mu_0$；
• 备择假设 $H_1\colon \mu \ne \mu_0$。

检验统计量 $\boxed{Z = \dfrac{\bar{X} - \mu_0}{S / \sqrt{n}}}$，若原假设成立，则 $Z \sim t(n-1)$。

有

$$\left\lbrace\begin{aligned} \bar{X} &\sim \mathcal{N}(\mu_0, \sigma^2 / n)\\ \dfrac{(n - 1)S^2}{n \sigma^2}&\sim \chi^2(n - 1)\\ Z &= \dfrac{(\bar{X} - \mu_0) / (\sigma \sqrt{n})}{\sqrt{((n - 1)S^2 / (n \sigma^2)) / (n - 1)}} \end{aligned}\right.$$

令 $X \sim t(n-1)$，有

• 备择假设 $H_1\colon \mu \ne \mu_0$（双侧检验）拒绝域

$$\left\lbrace z\colon \Pr(X \le z) \le \alpha / 2 \text{ or } \Pr(X \ge z) \le \alpha / 2 \right\rbrace$$

学生 t 分布

若随机变量 $X \sim \mathcal{N}(0, 1),\, Y \sim \chi^2(n)$ 独立，则随机变量

$$T = \dfrac{X}{\sqrt{Y/n}}$$

服从 $n$ 个自由度的学生 $t$ 分布，记作 $T \sim t(n)$。

正态总体样本均值和样本方差相互独立的证明

若 $X_1, \dots, X_n \sim \mathcal{N}(\mu, \sigma^2)$，则有 $\bar{X}^2$ 与 $S^2$ 相互独立。

（不严格地证明）有

$$\begin{aligned} f(x_1, \dots, x_n) &= (2 \pi \sigma^2)^{-n / 2} \exp\left( - \dfrac{\sum_i (x_i - \mu)^2}{2 \sigma^2} \right) \\ &= (2 \pi \sigma^2)^{-n / 2} \exp \left( - \dfrac{\sum_i (x_i - \bar{x})^2}{2 \sigma^2} \right) \exp \left( - \dfrac{n (\bar{x} - \mu)^2}{2 \sigma^2} \right) \end{aligned}$$

第一个 $\exp$ 可以看作 $S^2$，第二个 $\exp$ 可以看作 $\bar{X}$，即联合分布可以分解为 $\bar{X}$ 和 $S^2$ 的乘积，因此 $\bar{X}$ 与 $S^2$ 相互独立。

严格证明，有 $\bar{X} \sim \mathcal{N}(\mu, \sigma^2 / n)$，与 $\bar{X} - X_{j} = \dfrac{1}{n} \displaystyle \sum_{i \ne j} X_i - \dfrac{n - 1}{n}X_{j}$，于是

$$\begin{aligned} \bar{X} - X_{j} &\sim \mathcal{N}\left( \dfrac{(n - 1) \mu}{n} - \dfrac{(n - 1) \mu}{n}, (n - 1)\dfrac{\sigma^2}{n^2} + (n - 1)^2 \dfrac{\sigma^2}{n^2} \right) \\ &= \mathcal{N}\left(0, \dfrac{n - 1}{n} \sigma^2\right) \end{aligned}$$

两两之间的协方差有

$$\begin{aligned} \operatorname{Cov}(\bar{X} - X_{j}, \bar{X}) &= \operatorname{Cov}(\bar{X}, \bar{X}) - \operatorname{Cov}(X_j, \bar{X})\\ &= \dfrac{n - 1}{n} \sigma^2 \end{aligned}$$

而 $\operatorname{Cov}(X_{j}, \bar{X}) = \operatorname{Cov}(X_{j}, X_{j} / n) = \dfrac{\sigma^2}{n}$，同时 $\operatorname{Cov}(\bar{X}, \bar{X}) = \dfrac{\sigma^2}{n}$，即 $\bar{X}$ 与 $\bar{X} - X_{j}$ 不相关。

在联合正态分布中，不相关等价于相互独立，因此 $\bar{X}$ 与 $S^2$ 相互独立。

检验比较两个正态总体

已知方差 $\sigma_1^2, \sigma_2^2$，检验期望差 $\mu_1 - \mu_2$

样本 $X_1, \dots, X_{n_1} \sim \mathcal{N}(\mu_1, \sigma_1^2),\, Y_1, \dots, Y_{n_2} \sim \mathcal{N}(\mu_2, \sigma_2^2)$，取显著性水平 $\alpha$，检验 $\mu_1 = \mu_2$：

• 原假设 $H_0\colon \mu_1 = \mu_2$；
• 备择假设 $H_1\colon \mu_1 \ne \mu_2$（双侧检验）。

检验统计量 $\boxed{Z = \dfrac{(\bar{X} - \bar{Y}) - (\mu_1 - \mu_2)}{\sqrt{\sigma_1^2 / n_1 + \sigma_2^2 / n_2}}}$，若原假设成立，则 $Z \sim \mathcal{N}(0, 1)$。

令 $X \sim \mathcal{N}(0, 1)$，有

• 备择假设 $H_1\colon \mu_1 \ne \mu_2$（双侧检验）拒绝域

$$\left\lbrace z\colon \Pr(X \le z) \le \alpha / 2 \text{ or } \Pr(X \ge z) \le \alpha / 2 \right\rbrace$$

未知方差 $\sigma_1^2 = \sigma_2^2$，检验期望差 $\mu_1 - \mu_2$

样本 $X_1, \dots, X_{n_1} \sim \mathcal{N}(\mu_1, \sigma_1^2),\, Y_1, \dots, Y_{n_2} \sim \mathcal{N}(\mu_2, \sigma_2^2)$，取显著性水平 $\alpha$，检验 $\mu_1 = \mu_2$：

• 原假设 $H_0\colon \mu_1 = \mu_2$；
• 备择假设 $H_1\colon \mu_1 \ne \mu_2$（双侧检验）。

检验统计量 $\boxed{Z = \dfrac{(\bar{X} - \bar{Y}) - (\mu_1 - \mu_2)}{\left( \frac{1}{n_1} + \frac{1}{n_2} \right) \frac{(n_1 - 1)S_1^2 + (n_2 - 1)S_2^2}{n_1 + n_2 - 2}}}$，若原假设成立，则 $Z \sim t(n_1 + n_2 - 2)$。

令 $X \sim t(n_1 + n_2 - 2)$，有

• 备择假设 $H_1\colon \mu_1 \ne \mu_2$（双侧检验）拒绝域

$$\left\lbrace z\colon \Pr(X \le z) \le \alpha / 2 \text{ or } \Pr(X \ge z) \le \alpha / 2 \right\rbrace$$

未知方差 $\sigma_1^2 \ne \sigma_2^2$，检验期望差 $\mu_1 - \mu_2$*

Behrens-Fisher problem

Welech's 近似 $t$ 解法（Welch's approximate $t$ solution）：

令 $S^2 = S_1^2 / n_1 + S_2^2 / n_2$，则 $S^2$ 近似服从卡方分布。

检验统计量 $\boxed{Z = \dfrac{(\bar{X} - \bar{Y}) - (\mu_1 - \mu_2)}{\sqrt{S^2 / \mathord{?}}}}$。

近似自由度 $\ell \approx \dfrac{(g_1 + g_2)^2}{g_1^2 / (n_1 - 1) + g_2^2 / (n_2 - 1)}$，其中 $g_1 = S_1^2 / n_1, g_2 = S_2^2 / n_2$。

比较方差 $\sigma_1^2, \sigma_2^2$

F 检验

样本 $X_1, \dots, X_{n_1} \sim \mathcal{N}(\mu_1, \sigma_1^2)$，样本 $Y_1, \dots, Y_{n_2} \sim \mathcal{N}(\mu_2, \sigma_2^2)$，取显著性水平 $\alpha$，检验 $\sigma_1^2 = \sigma_2^2$：

• 原假设 $H_0\colon \sigma_1^2 = \sigma_2^2$；
• 备择假设 $H_1\colon \sigma_1^2 \ne \sigma_2^2$（双侧检验）。

检验统计量 $Z = \dfrac{S_1^2 / \sigma_1^2}{S_2^2 / \sigma_2^2}$，若原假设成立，则 $Z \sim F(n_1 - 1, n_2 - 2)$。

令 $X \sim F(n_1 - 1, n_2 - 2)$，有

• 备择假设 $H_1\colon \sigma_1^2 \ne \sigma_2^2$（双侧检验）拒绝域

$$\left\lbrace z\colon \Pr(X \le z) \le \alpha / 2 \text{ or } \Pr(X \ge z) \le \alpha / 2 \right\rbrace$$

F 分布

若随机变量 $X \sim \chi^2(n),\, Y \sim \chi^2(m)$ 独立，则随机变量

$$F = \dfrac{X/n}{Y/m}$$

服从 $n, m$ 个自由度的 $F$ 分布，记作 $F \sim F(n, m)$。

配对差异检验（paired difference test）

现实场景往往较为复杂，没有大量理想样本：

• 比较两种肥料的效果：不同农田本身条件不同。
  • 同一块田分两半，配对比较
• 检验药效：不同志愿者本身体质不同、病情不同。
  • 同一患者比较服药前后变化
• 比较机器学习算法性能：不同数据集性质不同。
  • 比较每组数据在不同算法下的准确度

配对差异检验

假设机器学习算法 $\mathfrak{L}_A, \mathfrak{L}_B$ 在数据集 $i$ 上的准确度分别服从正态分布 $\mathcal{N}(\mu^A_i, \sigma_1^2)$ 和 $\mathcal{N}(\mu^B_i, \sigma_2^2)$。$\sigma_1, \sigma_2$ 未知。取显著性水平 $\alpha$，比较两种算法的性能 $\sum_i \mu_i^A / n = \sum_i \mu_i^B / n$。

• 原假设 $H_0\colon \sum_i \mu_i^A / n = \sum_i \mu_i^B / n$；
• 备择假设 $H_1\colon \sum_i \mu_i^A / n \ne \sum_i \mu_i^B / n$（双侧检验）。

检验统计量 $\boxed{Z = \dfrac{\bar{X} - \bar{Y}}{\sqrt{\left( \frac{1}{n_1} + \frac{1}{n_2} \right) \frac{(n_1 - 1)S_1^2 + (n_2 - 1)S_2^2}{n_1 + n_2 - 2}}}}$，若原假设成立，则 $Z \sim t(n_1 + n_2 - 2)$。

令 $X \sim t(n_1 + n_2 - 2)$，有

• 备择假设 $H_1\colon \sum_i \mu_i^A / n \ne \sum_i \mu_i^B / n$（双侧检验）拒绝域

$$\left\lbrace z\colon \Pr(X \le z) \le \alpha / 2 \text{ or } \Pr(X \ge z) \le \alpha / 2 \right\rbrace$$

更多的例子：如比较两种不同的教学方法：

• 不同的学生现有成绩不同，优生可能方法 A 更有效，差生可能应该用方法 B
• 不同知识点不一样，不能对同一个学生先后应用两种不同的方法以比较
• 同一个学生对不同学科的天赋不同，不能对同一个学生的不同科目应用不
  同的教学方法

复杂的场景需要更为细致的分类和精妙的实验设计。

$p$-值（$p$-value / prob-value）

假设检验基本步骤（Neyman-Pearson's approach）：

1. 提出统计假设：原假设 $H_0$ 和备择假设 $H_1$
2. 针对两种假设确定能区分它们的统计量
3. 规定显著性水平 $\alpha$
4. 根据统计量确定拒绝域和接受域
5. 采样，从样本中计算出统计值
6. 判断统计值是否在拒绝域内，做出决策：「在显著性水平 $\alpha$ 下接受/拒绝原假设」

可以「丢掉」备择假设。

假设原假设为真，样本有多罕见？

统计假设：样本相互独立。中心极限定理：样本总体近似正态分布。

$$\begin{aligned} p &= \Pr(T \ge t \mid H_0)\\ p &= \Pr(T \le t \mid H_0)\\ p &= 2 \min\left\lbrace \Pr(T \le t \mid H_0), \Pr(T \ge t \mid H_0) \right\rbrace \end{aligned}$$

利用 $p$-值进行检验（Fisher's approach）：

1. 提出统计假设：原假设 $H_0$
2. 采样并从样本中计算出 $p$-值
3. 报告样本确切的 $p$-值，而非简单的「接受」或「拒绝」

$p$-值误用：如下图

原假设

将不同的假设作为原假设，可以得出完全相反的结论。

原假设反映了实验者的倾向：

• 同样的数据在不同倾向下有不同的假设
• 应选择较为中立和保守的原假设

原假设应该是清晰的，必须为分析概率分布提供基础。

应尽可能考虑多种不同的原假设。

非正态总体的参数检验*

样本 $X_1, \dots, X_n \sim \exp(\lambda)$，取显著性水平 $\alpha$，检验 $\lambda = \lambda_0$：

• 原假设 $H_0\colon \lambda = \lambda_0$

检验统计量 $\boxed{\bar{X}}$，有 $\mathbb{E}[\bar{X}] = \dfrac{1}{\lambda}$。

Gamma 分布

随机变量 $X$ 服从参数为 $k, \lambda > 0$ 的伽马分布，记作 $X \sim \Gamma(k, \lambda)$，若其概率密度函数为

$$f_X(x) = \dfrac{1}{\Gamma(k)} \lambda^k x^{k-1} \exp(-\lambda x),\quad x \ge 0$$

运用 Gamma 分布，有 $\exp(\lambda) = \Gamma(1, \lambda),\, \chi^2(n) = \Gamma\left(\frac{n}{2}, \frac{1}{2}\right)$，从而有 $n \bar{X} \sim \Gamma(n, \lambda),\, 2 \lambda n \bar{X} \sim \Gamma\left(n, \frac{1}{2}\right) = \chi^2(2n)$。

$p$ 值为 $2 \min\left\lbrace \Pr(\chi^2(2n) \le 2 \lambda n \bar{X}), \Pr(\chi^2 \ge 2 \lambda n \bar{X}) \right\rbrace$。

似然比检验（likelihood ratio test, LRT）

似然函数 $L(x; \theta_0),\, L(x; \theta_1)$ 分别表示两种假设下样本的概率。：

• $L(x; \theta_0)$：原假设下的似然函数
• $L(x; \theta_1)$：备择假设下的似然函数

则 $L(x; \theta_0) \ge L(x; \theta_1)$ 时更应该支持原假设 $H_0$（反之亦然）。即 $L(x; \theta_0) / L(x; \theta_1) \ge 1$ 更应该支持原假设。

Neyman-Pearson 引理

给定显著性 $\alpha$，LRT 是功效 $1 - \beta$ 最高的检验方法。

非参数假设检验

拟合优度检验（goodness of fit）

德军轰炸分布是否服从泊松分布？期末成绩得分是否符合正态分布？

步骤：

1. 将所有可能的结果分成不相交的事件 $\mathscr{E}_1, \dots, \mathscr{E}_m$；
2. 通过点估计确定猜测分布的部分参数，假设服从分布 $p(\mathscr{E}_i)$（可选）；
3. 检验统计量 $\boxed{\chi^2 = \displaystyle \sum_{i=1}^m \dfrac{(p(\mathscr{E}_i) - E_i)^2}{p(\mathscr{E}_i)}}$，其中 $E_i$ 是样本中事件 $\mathscr{E}_i$ 发生的频率，$k$ 是估计的未定参数个数；
4. 若服从分布，则统计量 $\chi^2 \approx \chi^2(m - k - 1)$；
5. $p$ 值显著性检验。

Pearson's chi-squared test

考虑二项分布 $X \sim \operatorname{Bin}(n, p)$，由中心极限定理有 $Z = \dfrac{X - np}{\sqrt{np (1 - p)}} \xrightarrow[]{D} \mathcal{N}(0, 1)$，于是 $Z^2 \xrightarrow[]{D} \chi^2(1)$。

令 $p_1 = p, p_2 = 1 - p, Y = n - X$，于是有 $Z^2 = \dfrac{(X - np_1)^2}{np_1} + \dfrac{(Y - np_2)^2}{np_2} \xrightarrow[]{D} \chi^2(1)$。

多项式分布也可以得出相似的结论。

独立性检验（statistical independence）

唯一的高中内容？然而我也忘了。

两种因素对样本有影响吗？数据样本的特征和它的分类是否相互独立？

步骤：

1. 根据 $r$ 种分类和 $c$ 种特征，构建 $r \times c$ 的「列联表」（contingency table/cross tabulation/crosstab）；
2. 从样本中估计分类与特征的分布函数 $p_{i \odot }, p_{\odot j}$^[1]；
3. 若分类与特征相互独立，有 $n_{ij} \approx n p_{i \odot } p_{\odot j}$；
4. 检验统计量 $\boxed{\chi^2 = \displaystyle \sum_{i=1}^{r}\sum_{j=1}^{c} \dfrac{(n_{ij} - np_{i \odot } p_{\odot j})^2}{n p_{i \odot } p_{\odot j}}}$；
5. 若相互独立，则统计量 $\chi^2 \approx \chi^2((r-1)(c-1))$；
6. $p$ 值显著性检验。

同质性检验（statistical homogeneity）

两种因素对样本有影响吗？两种机器学习算法在不同数据集上有性能差异吗？

步骤：

1. 根据 2 种算法和 $c$ 个数据集，构建 $2 \times c$ 的「列联表」（contingency table/cross tabulation/crosstab）；
2. 从样本中估计每组数据的正确率 $p_{j}$；
3. 若没有性能差异，则 $n_{1j} \approx n_{2j} \approx p_{j}$；
4. 检验统计量 $\boxed{\chi^2 = \displaystyle \sum_{i=1}^{2}\sum_{j=1}^{c} \dfrac{(n_{ij} - p_{j})^2}{p_{j}}}$；
5. 若相互独立，则统计量 $\chi^2 \approx \chi^2(c-1)$；
6. $p$ 值显著性检验。

符号检验（sign test）

检验总体的中位数 $m = m_0$？检验上了课的学生 GPA 变高？

步骤：

1. 对每个样本 $X_1, \dots, X_n$ 检验是否 $X_1 < m_0$ 并记录 $+ / -$；
2. 若原假设成立，则 $\#- \sim \operatorname{Bin}\left(n, \frac{1}{2}\right)$；
3. $p$ 值显著性检验。

对于上面 GPA 的检验，就是把步骤中的 $\#-$ 换成 $\#+$，$\frac{1}{2}$ 换成 $p > \frac{1}{2}$。

秩和检验（rank-sum test）

Mann-Whitney-Wilcoxon $U$ test

这里的 rank 实际是「排名」，「排名和检验」比「秩和检验」更清晰易懂。

两个总体 $\mathscr{D}_1, \mathscr{D}_2$ 是否有差不多 $\Pr(X > Y) = \Pr(Y > X)$，其中 $X \in \mathscr{D}_1, Y \in \mathscr{D}_2$？

步骤：

1. 采样样本 $X_1, \dots, X_{n_1} \sim \mathscr{D}_1, Y_1, \dots, Y_{n_2} \sim \mathscr{D}_2$；
2. 将 $X_1, \dots, X_{n_1}, Y_1, \dots, Y_{n_2}$ 按大小顺序排序，并记录每个样本的排名；
3. 检验统计量 $\boxed{\min\left\lbrace U_1, U_2 \right\rbrace}$，其中
   • $U_1 = n_1 n_2 + \dfrac{n_1 (n_1 + 1)}{2} - R_1$
   • $U_2 = n_1 n_2 + \dfrac{n_2 (n_2 + 1)}{2} - R_2$
   • $R_1, R_2$ 分别表示两组样本的排名之和
   • $U_1 + U_2 = n_1 n_2$^[2]；
   • $U$ 统计量外部资料
4. 若原假设成立，小样本时查表，大样本时利用中心极限定理；
5. $p$ 值显著性检验。

符号秩检验（Wilcoxon signed-rank test）

样本 $X_1, \dots, X_n$ 来自总体 $\mathscr{D}$，检验 $\mathscr{D}$ 是否关于 0 轴对称？

步骤：

1. 将样本按 $|X_i|$ 排序，并记录排名；
2. 检验统计量 $\boxed{T^{+} = \sum_{i\colon X_i > \theta}R_i}$，其中 $R_i$ 表示 $X_i$ 在上述排序中的排名，$\theta$ 为检验的中位数；
3. 若原假设成立，小样本时查表，大样本时中心极限定理有 $T^{+} \sim \mathcal{N}(\mu, \sigma^2)$，其中 $\mathbb{E}[T^{+}] = \dfrac{n(n+1)}{4}, \operatorname{Var} [T^{+}] = \dfrac{n(n+1)(2n+1)}{24}$；
4. $p$ 值显著性检验。

---

1. PPT 用的是 \cdot $\cdot$，可惜不太清晰，我换成了 \odot $\odot$。不过前面用的还是前者，但我懒得改了。 ↩︎

2. $U_1 + U_2 = 2 n_1 n_2 + \dfrac{1}{2} \left( n_1^2 + n_2^2 + n_1 + n_2 \right) - \dfrac{(n_1 + n_2)(n_1 + n_2 + 1)}{2} = n_1 n_2$。 ↩︎