连续分布

连续随机变量

有关随机变量的内容，可以参见前面的笔记「随机变量」。

一个随机变量 $X\colon \Omega \to \R$ 是连续（continuous）的，若其累积分布函数 CDF 可以表示为

$$F_X(x) = \Pr[X \le x] = \int_{-\infty}^x f_X(u) \d u$$

的形式。其中 $f_X\colon \R \to [0, \infty )$ 是一个可积函数，称为 $X$ 的概率密度函数（probability density function, pdf）。

密度函数 $f$ 并不唯一由上式确定，概率密度函数实际上有无穷多个。

若 $F_X$ 可微（differentiable），一般取 $f_X(x) = F_X'(x)$。

对于连续随机变量 $X$，有（it holds that）

$$\forall x \in \R,\, \Pr[X = x] = 0$$

概率质量函数 pmf 是一个概率，概率密度函数 pdf 不是概率，而是 proportion(density, 密度)

$$\Pr[x < X \le x + \Delta x] = F_X(x + \Delta x) - F_x(x) \approx f_X(x) \Delta x$$

$f_X$ 是一个连续随机变量 $X\colon \Omega \to \R$ 的 pdf 当且仅当

$$\int_{-\infty}^\infty f_X(x) \d x = 1$$

与 $\forall x \in \R,\, f_X(x) \ge 0$。

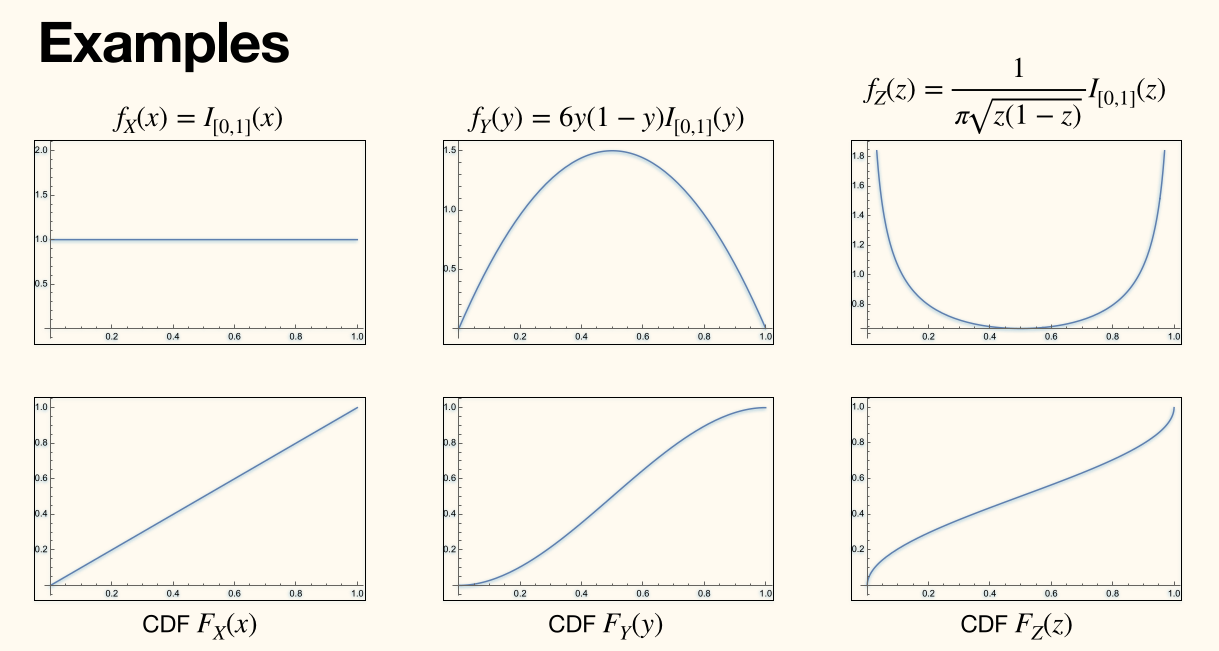
上面的 $I_{[0, 1]}$ 将自变量范围限制在了 $[0, 1]$ 中。

连续概率空间*

令 $\mathscr{I}$^[1] 是 $\R$ 中全部开区间的集合，博雷尔（Borel）$\sigma$-代数 $\mathscr{B}$（Borel $\sigma$-field）是最小的包含 $\mathscr{I}$ 的 $\sigma$-代数。每个 $B \in \mathscr{B}$ 称为博雷尔集（Borel set），是一个对开区间由可数个 $\cap , \cup , \setminus$ 进行可数次操作得到的集合。

对于博雷尔集 $B \in \mathscr{B}$，勒贝格积分（Lebesgue integral）

$$\mu(B) \coloneqq \Pr[X \in B] = \int_B f_X(x) \d x = \int_{-\infty}^\infty I_B(x) \d F_X(x)$$

则 $(\R, \mathscr{B}, \mu)$ 是一个良定义的概率空间。

若 $g\colon \R \to \R$ 是博雷尔可测（Borel-measurable）的，即 $\forall y \in \R,\, \left\lbrace x \in \R \mid g(x) \le y \right\rbrace \in \mathscr{B}$，则 $g(X)$ 也是一个随机变量。

勒贝格积分

这部分只是「科普性质」的「简单介绍」。

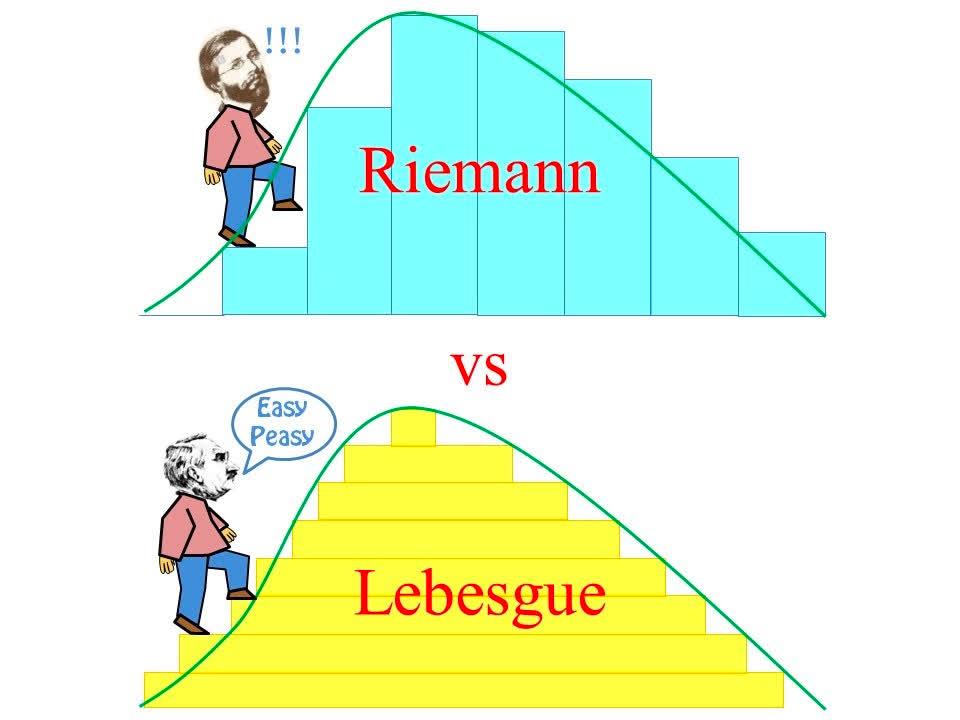
令 $(\R, \mathscr{B}, \mu)$ 是一个概率空间（测度空间）。

假设 $f$ 是（博雷尔）可测的，且非负，对于 $B \in \mathscr{B}$，定义

$$f^{*}(t) = \mu(\left\lbrace x \in B \mid f(x) > t \right\rbrace)$$

勒贝格积分（Lebesgue integral）定义为

$$\int_B f(x) \d \mu(x) = \int_0^\infty f^{*}(t) \d t$$

对于一般的 $f$，可令 $f=f^{+}-f^{-}$，其中 $f^{+}, f^{-}$ 非负。

病态（Pathological）例子

• 不可测集的例子
  • 维塔利集（Vitali set）：$V \subseteq [0, 1]$，包含每个有理数陪集的一个元素。
  • contains a single point from each coset of $\Q$ in $\R$
• 勒贝格可积但黎曼不可积的函数
  • 狄利克雷函数（Dirichlet function）：有理数的指示函数。
• $[0, 1]$ 的不可数子集，但测度为 0
  • 康托尔集（Cantor set）
  • 

联合分布

随机变量 $X, Y$ 的联合分布函数（joint distribution function）是函数 $F_{X, Y}\colon \R^2 \to [0, 1]$ 定义为

$$F_{X, Y}(x, y) = \Pr[X \le x \cap Y \le y]$$

随机变量 $X, Y$ 是以联合概率密度函数（joint pdf）$f_{X, Y}\colon \R^2 \to[0, \infty )$ （联合）连续的（(jointly) continuous）^[2]，若对任意 $x, y \in \R$ 有

$$F_{X, Y}(x, y) = \int_{v=-\infty }^y \int_{u=-\infty }^x f_{X, Y}(u, v) \d u \d v$$

设 $F_{X, Y}$ 充分可微（sufficiently differentiable），则

$$f_{X, Y}(x, y) = \frac{\partial^2}{\partial x \partial y} F_{X, Y}(x, y)$$

边缘分布

$X, Y$ 的边缘分布函数（marginal distribution function）为

$$\begin{aligned} F_X(x) = \Pr[X \le x] = F_{X, Y}(x, \infty ) = \int_{-\infty }^x \int_{-\infty }^\infty f_{X, Y}(u, y) \d y \d u\\ F_Y(y) = \Pr[Y \le y] = F_{X, Y}(\infty , y) = \int_{-\infty }^y \int_{-\infty }^\infty f_{X, Y}(x, v) \d x \d v \end{aligned}$$

$X, Y$ 的边缘密度函数（marginal density function）为

$$\begin{aligned} f_X(x) = \int_{-\infty }^\infty f_{X, Y}(x, y) \d y\\ f_Y(y) = \int_{-\infty }^\infty f_{X, Y}(x, y) \d x \end{aligned}$$

独立性

随机变量 $X, Y$ 是独立的（independent），若对任意 $x, y \in \R$ 有 $X \le x$ 与 $Y \le y$ 是独立事件，即

$$F_{X, Y}(x, y) = F_X(x) F_Y(y)$$

对于连续随机变量 $X, Y$，等价于

$$f_{X, Y}(x, y) = f_X(x) f_Y(y)$$

对于博雷尔可测的 $g, h\colon \R \to \R$（即 $g(X), h(Y)$ 是随机变量），则 $X, Y$ 独立可以推出 $g(X), h(Y)$ 也是独立的。

• 因为 $X$ 是 $\Sigma$-可测的，$g$ 是博雷尔可测的，于是 $g(X)$ 是 $\Sigma$-可测的。

条件分布

令 $X$ 是一个连续随机变量，$A$ 是一个事件，且 $\Pr(A) > 0$，则 $X$ 在 $A$ 条件下的条件分布函数（conditional distribution function）为

$$F_{X\mid A}(x) = \Pr[X \le x \mid A] = \int_{-\infty }^x f_{X\mid A}(u) \d u$$

其中密度函数 $f_{X\mid A} = \dfrac{\d F_{X \mid A}(x)}{\d x}$。

全概率法则（离散）

对于 $\Omega$ 的划分 $B_1, \dots, B_n$，且任意 $B_i$ 有 $\Pr(B_i) > 0$，有

$$f_X(x) = \sum_{i=1}^n \Pr(B_i) f_{X \mid B_i}(x)$$

证明

对下式两边同时求导即可

$$\Pr[X \le x] = \sum_{i=1}^n \Pr(B_i) \Pr[X \le x \mid B_i]$$

对于（联合）连续随机变量 $X, Y$，则 $X$ 在给定 $Y = y$ 条件下的条件分布函数为

$$F_{X \mid Y}(x \mid y) = \Pr[X \le x \mid Y = y] = \int_{-\infty }^x \dfrac{f_{X, Y}(u, y)}{f_Y(y)} \d u$$

---

这个定义是有意义的，因为

$$\begin{aligned} \Pr[X \le x \mid y \le Y \le y + \d y] &= \dfrac{\Pr[X \le x \cap y \le Y \le y + \d y]}{\Pr[y \le Y \le y + \d y]}\\ &= \dfrac{\int_{u=-\infty }^x f_{X, Y}(u, y)\d y \d u}{f_Y(y) \d y}\\ &= \int_{u=-\infty }^x \dfrac{f_{X, Y}(u, y)}{f_Y(y)} \d u \end{aligned}$$

$F_{X \mid Y}$ 的条件密度函数定义为

$$f_{X \mid Y} (x \mid y) = \dfrac{f_{X, Y}(x, y)}{f_Y(y)}$$

对于任意 $y$ 使得 $f_Y(y) > 0$。

全概率法则

令 $B \subseteq \R$ 是一个集合（博雷尔集），对于联合连续随机变量 $X, Y$，其中 $Y$ 在 $\Omega_Y \subseteq \R$ 上有着正密度，则有

$$\begin{aligned} \Pr[X \in B] &= \int_{\Omega_Y} \Pr[X \in B \mid Y = y] \cdot f_Y(y) \d y\\ &= \int_{\Omega_Y}f_Y(y) \int_{B} \dfrac{f_{X, Y}(x, y)}{f_Y(y)} \d x \d y\\ &= \boxed{ \int_{\Omega_Y}f_Y(y) \int_{B} f_{X \mid Y}(x \mid y) \d x \d y } \end{aligned}$$

期望

以 $f_X$ 为 pdf（与 CDF $F_X$）的连续随机变量 $X$ 的期望（expectation，亦称为均值 mean）定义为

$$\mathbb{E}[X] = \int_{-\infty}^\infty x f_X(x) \d x = \int_{-\infty }^{\infty }x \d F_X(x)$$

$X$ 的 $k$-阶矩（$k$-th moment）类似地定义为

$$\mathbb{E}[X^{k}] = \int_{-\infty}^\infty x^{k} f_X(x) \d x = \int_{-\infty }^{\infty }x^{k} \d F_X(x)$$

这些定义当积分存在时，都是良定义的。

双重计数法

若连续随机变量 $X$ 仅取非负值^[3]，则

$$\mathbb{E}[X] = \int_0^{\infty }\left(1-F_X(x)\right)\d x = \int_0^{\infty }\Pr[X > x] \d x$$

证明

$$\begin{aligned} \int_0^{\infty }\left(1-F_X(x)\right) \d x &= \int_0^{\infty }\Pr[X > x] \d x\\ &= \int_0^{\infty } \left( \int_x^{\infty }f_X(u)\d u \right) \d x\\ &= \int_{u=0}^{\infty }f_X(u)\int_{x=0}^{u} \d x \d u\\ &= \int_{0}^{\infty} u f_X(u) \d u\\ &= \mathbb{E}[X] \end{aligned}$$

LOTUS

若 $X$ 是一个连续随机变量，且 $g(X)$ 是一个随机变量，则

$$\mathbb{E}[g(X)] = \int_{-\infty}^\infty g(x) f_X(x) \d x$$

证明

先假设 $g \ge 0$，令 $B_y = \left\lbrace x \mid g(x) > y \right\rbrace$，于是

$$\begin{aligned} \mathbb{E}[g(X)] &= \int_{0}^\infty \Pr[g(X) > y] \d y\\ &= \int_0^{\infty }\int_{B_y} f_X(x) \d x \d y\\ &= \int_{-\infty }^{\infty }f_X(x)\int_0^{g(x)} \d y \d x\\ &= \int_{-\infty }^{\infty }g(x) f_X(x) \d x \end{aligned}$$

对于一般的 $g\colon \R \to\R$，可令 $g = g^{+} - g^{-}$，其中 $g^{+}, g^{-}$ 非负，于是

$$\begin{aligned} \mathbb{E}[g(X)] &= \mathbb{E}[g^{+}(X)] - \mathbb{E}[g^{-}(X)]\\ &= \int_{-\infty }^{\infty }g^{+}(x) f_X(x) \d x - \int_{-\infty }^{\infty }g^{-}(x) f_X(x) \d x\\ &= \int_{-\infty }^{\infty }g(x) f_X(x) \d x \end{aligned}$$

期望的线性性质就略了，证明也是类似的，就不再写一次了。

额外写一个 $\mathbb{E}[X + Y] = \mathbb{E}[X] + \mathbb{E}[Y]$ 的证明：

证明

$$\begin{aligned} \mathbb{E}[X + Y] &= \iint_{\R^2} (x + y) f_{X, Y}(x, y) \d x \d y\\ &= \iint_{\R^2} x f_{X, Y}(x, y) \d x \d y + \iint_{\R^2} y f_{X, Y}(x, y) \d x \d y\\ &= \int_{-\infty }^{\infty }x f_{X}(x) \d x + \int_{-\infty }^{\infty }y f_{Y}(y) \d y\\ &= \mathbb{E}[X] + \mathbb{E}[Y] \end{aligned}$$

期望的单调性：

1. 若 $X \ge 0$，则 $\mathbb{E}[X] \ge 0$；
2. 若 $X \ge Y$，则 $\mathbb{E}[X] \ge \mathbb{E}[Y]$。

接下来是全期望，离散的部分就不写了，可见前面的笔记。

$$\begin{aligned} \mathbb{E}[\mathbb{E}[X \mid Y]] &= \int_{-\infty }^{\infty } \mathbb{E}[X \mid y] f_Y(y) \d y\\ &= \int_{-\infty }^{\infty } f_Y(y) \int_{-\infty }^{\infty } x f_{X \mid Y}(x \mid y) \d x \d y\\ &= \int_{-\infty }^{\infty } f_Y(y) \int_{-\infty }^{\infty } x \dfrac{f_{X, Y}(x, y)}{f_Y(y)} \d x \d y\\ &= \int_{-\infty }^{\infty } \int_{-\infty }^{\infty } x f_{X, Y}(x, y) \d x \d y\\ &= \int_{-\infty }^{\infty } x f_X(x) \d x\\ &= \mathbb{E}[X] \end{aligned}$$

对独立随机变量 $X, Y$，可根据变量代换证明期望的乘积：

$$\begin{aligned} \mathbb{E}[XY] &= \iint_{\R^2} xy f_{X, Y}(x, y) \d x \d y\\ &= \iint_{\R^2} xy f_X(x) f_Y(y) \d x \d y\\ &= \left( \int_{-\infty }^{\infty } x f_X(x) \d x \right) \left( \int_{-\infty }^{\infty } y f_Y(y) \d y \right)\\ &= \mathbb{E}[X] \mathbb{E}[Y] \end{aligned}$$

连续概率分布

连续均匀分布

随机变量 $X$ 在 $a$ 到 $b$ 的区间^[4]上是均匀分布（uniform）的，若其概率密度函数 pdf 为

$$f(x) = \begin{cases} \dfrac{1}{b - a} & \text{if } a \le x \le b\\ 0 & \text{otherwise} \end{cases}$$

与累积分布函数 CDF 为

$$F(x) = \begin{cases} 0 & \text{if } x \le a\\ \dfrac{x - a}{b - a} & \text{if } a < x \le b\\ 1 & \text{if } x > b \end{cases}$$

期望（与离散均匀分布的期望相同）

$$\begin{aligned} \mathbb{E}[X] &= \int_a^b \dfrac{x}{b - a} \d x\\ &= \dfrac{a+b}{2} \end{aligned}$$

方差（这与离散均匀分布的方差不同）

$$\begin{aligned} \operatorname{Var} [X] &= \mathbb{E}[X^2] - \mathbb{E}[X]^2\\ &= \int_a^b \dfrac{x^2}{b-a}\d x - \left( \dfrac{a+b}{2} \right)^2\\ &= \dfrac{(b-a)^2}{12} \end{aligned}$$

对于连续均匀随机变量 $X$，有期望

$$\boxed{ \mathbb{E}[X] = \dfrac{a+b}{2} }$$

与方差

$$\boxed{ \operatorname{Var} [X] = \dfrac{(b-a)^2}{12} }$$

拒绝采样（Rejection Sampling）

令 $X$ 是 $[a, b]$ 上的一个均匀随机变量，则对任意 $[c, d] \subseteq [a, b]$ 有

$$\Pr(X \in [c, d]) = \dfrac{d-c}{b-a}$$

同时给定 $X \in [c, d]$ 条件，$X$ 的条件分布在 $[c, d]$ 上也是均匀的：

$$\Pr(X \le x \mid X \in [c, d]) = \begin{cases} 0 & \text{if } x < c\\ \dfrac{x-c}{d-c} & \text{if } c \le x \le d\\ 1 & \text{if } x > d \end{cases}$$

因为有

$$\Pr(X \le x \mid X \in [c, d]) = \dfrac{\Pr(X \in [a, x] \cap [c, d])}{\Pr(X \in [c, d])} = \dfrac{\Pr(X \in [c, x])}{\Pr(X \in [c, d])}$$

Induced probability distribution (诱导概率分布)

对于 pdf 为 $f_X$ 的连续随机变量 $X$，若 $Y = g(X)$ 是一个随机变量（$g\colon \R \to \R$ 博雷尔可测），则其 pdf $f_Y$ 为什么呢？

不妨假设 $g$ 单调递增，则 $Y$ 的 CDF 是

$$\begin{aligned} F_Y(y) &= \Pr[Y \le y]\\ &= \Pr[g(X) \le y]\\ &= \int_{\left\lbrace x \mid g(x) \le y \right\rbrace} f_X(x) \d x\\ &= \int_{-\infty }^{g^{-1}(y)} f_X(x) \d x\\ &= F_X(g^{-1}(y)) \end{aligned}$$

于是 $Y$ 的 pdf 为

$$\begin{aligned} f_Y(y) &= \dfrac{\d F_Y(y)}{\d y}\\ &= \dfrac{\d F_X(g^{-1}(y))}{\d y}\\ &= f_X(g^{-1}(y)) \dfrac{\d g^{-1}(y)}{\d y}\\ &= f_X(g^{-1}(y)) \left| \dfrac{\d g^{-1}(y)}{\d y} \right|\\ &= f_X(g^{-1}(y)) \left| \dfrac{1}{g'(g^{-1}(y))} \right| \end{aligned}$$

$g$ 单调递减结果是一样的。

最后绝对值里面要再看看，课件上写的是 $\dfrac{1}{g'(y)}$。

逆变换采样（Inverse Transform Sampling）

又称「逆万流齐一」或「逆万流归宗」。

令随机变量 $U$ 在 $[0, 1]$ 上均匀分布。令 $F\colon \R \to [0, 1]$ 是一个 CDF

• 若 $F$ 是连续的，则随机变量 $X = F^{-1}(U)$ 有 CDF 为 $F$；
• 若 $F$ 是一个整数值的离散随机变量的 CDF，则离散随机变量 $X = k$ 当且仅当 $F(k-1) < U \le F(k)$ 有 CDF 为 $F$。

反函数 $F^{-1}$ 给出了随机变量 $X$ 的分位点（quantile）^[5]：

$$\begin{aligned} \Pr[X \le x] &= \Pr[F^{-1}(U) \le x]\\ &= \Pr[U \le F(x)]\\ &= \dfrac{F(x) - 0}{1 - 0}\\ &= F(x) \end{aligned}$$

与

$$\begin{aligned} \Pr[X = k] &= \Pr[F(k-1) < U \le F(k)]\\ &= F(k) - F(k-1) \end{aligned}$$

Stochastic Domination and Coupling

若随机变量 $X, Y$ 满足

$$F_X(u) \le F_Y(u),\, \forall u \in \R$$

则称 $X$ 随机支配^[6] $Y$，记作 $X \succeq_{\mathrm{st}} Y$。

用另一种说法就是，对任意 $u \in \R$，都有 $\Pr[X \ge u] \ge \Pr[Y \ge u]$。

上图中，红线对应的随机变量随机支配黑线对应的随机变量。

上图中，红线对应的随机变量，与黑线对应的随机变量不可比。

$X \succeq_{\mathrm{st}} Y$ 当且仅当存在 $X, Y$ 的一个耦合（coupling）$(X', Y')$，满足边缘分布 $F_{X'} = F_X,\, F_{Y'} = F_Y$，使得 $\Pr(X' \ge Y') = 1$（即 $X' \ge Y'$ 几乎必然发生）。

证明

令 $U$ 为 $[0, 1]$ 上的均匀随机变量，$X' = F_X^{-1}(U),\, Y' = F_Y^{-1}(U)$。

若 $X, Y$ 是离散的，则令 $X' = k \iff F_X(k-1) < U \le F_X(k),\, Y' = k \iff F_Y(k-1) < U \le F_Y(k)$。

通过「逆万流归宗」，边缘分布 $F_{X'} = F_X,\, F_{Y'} = F_Y$，且有 $X' = F_{X}^{-1}(U) \ge F_Y^{-1}(U) = Y'$，因为对任意 $u \in \R$ 都有 $F_X(u) \le F_Y(u)$。

指数分布

随机变量 $X$ 是一个以 $\lambda > 0$ 为参数的指数分布（exponential distribution），若其概率密度函数 pdf 为

$$f(x) = \lambda \e^{- \lambda x}$$

与累积分布函数 CDF 为

$$F(x) = 1 - \e^{- \lambda x},\quad x \ge 0$$

指数分布是几何分布的连续极限版本。

每隔 $\delta$ 时间间隔，进行一次 i.i.d. 伯努利试验（$p = \lambda \delta$），并令随机变量 $X$ 表示第一次成功的时间，则

$$\begin{aligned} \Pr(X > x) &= (1 - p)^{\frac{x}{\delta}}\\ &= (1 - \lambda \delta)^{\frac{x}{\delta}}\\ &\to \e^{- \lambda x} \end{aligned}$$

当 $\delta \to 0$ 时。

几何分布也可以从指数分布得到，对于 $X \sim \exp(\lambda)$，有 $\left\lceil X \right\rceil \sim \operatorname{Geo}(1 - \e^{- \lambda})$。因为

$$\begin{aligned} \Pr(\left\lceil X \right\rceil = k) &= \Pr(k-1 < X \le k)\\ &= F(k) - F(k-1)\\ &= (1 - \e^{- \lambda k}) - (1 - \e^{- \lambda (k-1)})\\ &= \e^{- \lambda (k-1)} (1 - \e^{- \lambda}) \end{aligned}$$

期望

$$\begin{aligned} \mathbb{E}[X] &= \int_0^{\infty } x \lambda \e^{- \lambda x} \d x\\ &= - \int_{0}^{\infty} x \d \e^{- \lambda x}\\ &= \left(- x \e^{- \lambda x}\right)\as_{0}^{\infty} + \int_{0}^{\infty} \e^{- \lambda x} \d x\\ &= \dfrac{1}{\lambda} \end{aligned}$$

或者也可以这样算：

$$\begin{aligned} \mathbb{E}[X] &= \int_{0}^{\infty} (1 - F(x)) \d x\\ &= \int_{0}^{\infty} \e^{- \lambda x} \d x\\ &= \dfrac{1}{\lambda} \end{aligned}$$

而二阶矩

$$\begin{aligned} \mathbb{E}[X^2] &= \int_{0}^{\infty} x^2 \lambda \e^{- \lambda x} \d x\\ &= \dfrac{2}{\lambda^2} \end{aligned}$$

从而方差

$$\begin{aligned} \operatorname{Var} [X] &= \mathbb{E}[X^2] - \mathbb{E}[X]^2\\ &= \dfrac{2}{\lambda^2} - \dfrac{1}{\lambda^2}\\ &= \dfrac{1}{\lambda^2} \end{aligned}$$

对于指数分布 $X \sim \exp(\lambda)$，有期望

$$\boxed{ \mathbb{E}[X] = \dfrac{1}{\lambda} }$$

与方差

$$\boxed{ \operatorname{Var} [X] = \dfrac{1}{\lambda^2} }$$

与几何分布类似，指数分布也有「无记忆性」，即对于 $s, t \ge 0$，有

$$\Pr(X > s + t \mid X > t) = \Pr(X > s)$$

若 $X_1, \cdots, X_n$ 是独立的指数分布随机变量，且 $X_i \sim \exp(\lambda_i)$，则 $X = \min\left\lbrace X_1, \cdots, X_n \right\rbrace$ 是一个指数分布随机变量，且 $X \sim \exp(\sum_{i=1}^n \lambda_i)$。

证明

$$\begin{aligned} \Pr\left( \min_{1 \le i \le n} X_i > x \right) &= \Pr\left( \bigcap_{1\le i \le n}(X_i > x) \right) \\ &= \prod_{i=1}^{n} \Pr(X_i > x)\\ &= \prod_{i=1}^{n} \e^{- \lambda_i x}\\ &= \e^{- \sum_{i=1}^{n} \lambda_i x} \end{aligned}$$

泊松点过程

泊松点过程是一个连续时间的随机过程，其间隔时间 $X_i$ 是独立的指数分布随机变量，即 $X_i \sim \exp(\lambda)$。

具体来说，泊松过程（Poisson process）$\left\lbrace N(t) \mid t \ge 0 \right\rbrace$ 与参数（rate）$\lambda > 0$ 是一个连续时间过程定义如下——假设我们有这样一个闹钟：

• $N(t)$ 表示在闹钟在时间 $t$ 前响起的次数，初始状态 $N(0) = 0$；
• 任意两个连续的响铃之间的时间间隔（interarrival time）$X_i$ 是独立的指数分布随机变量，即 $X_i \sim \exp(\lambda)$。

由于无记忆性与最小性，由 $k$ 个独立的以 $\lambda$ 为相同参数的这样的闹钟，可以视作一个以 $\lambda k$ 为参数的闹钟。

对于任意 $t, s \ge 0$ 与自然数 $n$，有

$$\begin{aligned} \Pr(N(t+s) - N(s) = n) &= \Pr(N(t) = n)\\ &= \e^{-\lambda t} \dfrac{(\lambda t)^n}{n!} \end{aligned}$$

证明

$X_i$ 表示第 $i-1, i$ 个闹钟响起的时间间隔，于是有 $X_i \sim \exp(\lambda)$。

零次有

$$\begin{aligned} \Pr(N(t) = 0) &= \Pr(X_1 > t)\\ &= \e^{-\lambda t} \end{aligned}$$

一次有

$$\begin{aligned} \Pr(N(t) = 1) &= \Pr(X_1 \le t \cap X_1 + X_2 > t)\\ &= \int_0^t f_{X_1}(x) \Pr(X_2 > t - x) \d x\\ &= \int_0^t \lambda \e^{-\lambda x} \e^{-\lambda(t-x)} \d x\\ &= \int_0^t \lambda \e^{-\lambda t} \d x\\ &= \lambda t \e^{-\lambda t} \end{aligned}$$

数学归纳法，设 $\Pr(N(t) = n) = \e^{-\lambda t} \dfrac{(\lambda t)^n}{n!}$，则有

$$\begin{aligned} \Pr(N(t) = n+1) &= \int_0^t f_{X_1}(x) \Pr(N(t-x) = n) \d x\\ &= \int_0^t \lambda \e^{-\lambda x} \e^{-\lambda(t-x)} \dfrac{(\lambda(t-x))^n}{n!} \d x\\ &= \dfrac{\lambda^{n+1}}{n!} \e^{-\lambda t} \int_0^t (t-x)^n \d x\\ &= \e^{-\lambda t} \dfrac{(\lambda t)^{n+1}}{(n+1)!} \end{aligned}$$

正态分布（高斯分布）

想象一个场景，在一个高维空间中采样一个均匀随机单位向量 $U \in \R^n$ 使得 $\left\lVert U \right\rVert_2 = 1$。

有一种方案就是随机采样 i.i.d. $X_1, \dots, X_n \in \R$，并将其标准化

$$U = \dfrac{(X_1, \dots, X_n)}{\left\lVert (X_1, \dots, X_n) \right\rVert_2}$$

但是这样其实并不正确。考虑二维的情况，$X_1, X_2$ 就像是在单位正方形内是均匀的，然后再将其标准化到单位圆上，这样得到的在单位圆上的分布是不均匀的。图就懒得画了。

$U$ 需要在单位球体上是均匀的，所以需要 $(X_1, \cdots, X_n)$ 的联合密度是球面对称的，即在给定 $\left\lVert \bm{x} \right\rVert_2 = \left\lVert \bm{y} \right\rVert_2$ 时要有

$$f_{\bm{X}}(\bm{x}) = \prod_{i=1}^{n} f_{X_i}(x_i) = \prod_{i=1}^{n} f_{X_i}(y_i) = f_{\bm{X}}(\bm{y})$$

而这就要求了随机变量的概率密度函数

$$f(x) \propto \exp(-c x^2)$$

说明

设概率密度函数 $f\colon \R \to \R^{+}$，并假设 $f(0) \ne 0$。

考虑二维情况，采样到 $(x, y)$ 时，有

$$f(x) f(y) = f(\sqrt{x^2 + y^2}) f(0)$$

定义 $g(x) = \ln \dfrac{f(x)}{f(0)}$，则得到

$$g(x) + g(y) = g(\sqrt{x^2 + y^2})$$

则存在 $a \in \R$ 使得

$$g(x) = a x^2$$

于是有 $f(x) = f(x) \e^{a x^2}$，且 $a < 0$。

证明略。

随机变量 $X$ 是一个以 $\mu \in \R, \sigma > 0$ 为参数的正态分布（normal distribution），记作 $X \sim \mathcal{N}(\mu, \sigma^2)$，若其概率密度函数 pdf 为

$$f(x) = \dfrac{1}{\sqrt{2\pi}\sigma} \exp\left( -\dfrac{(x - \mu)^2}{2\sigma^2} \right)$$

当 $\mu = 0, \sigma = 1$ 时，称为标准正态分布（standard normal distribution），有

$$f_X(x) = \dfrac{1}{\sqrt{2\pi}} \exp\left( -\tfrac{x^2}{2} \right)$$

这个概率分布是良定义的，因为有高斯积分

$$\int_{-\infty }^{\infty} \e^{-x^2} \d x = \sqrt{\pi}$$

正态分布是二项分布的连续极限，这是「德莫弗-拉普拉斯定理」（De Moivre-Laplace theorem）。

这个定理是中心极限定理（central limit theorem, CLT）的一个特例，即多个独立随机变量的和近似服从正态分布。

期望显然有 $\mathbb{E}[X] = \mu$，因为 pdf $f_X(x)$ 是关于 $x = \mu$ 对称的。

而方差

$$\begin{aligned} \operatorname{Var} [X] &= \dfrac{1}{\sqrt{2 \pi}\sigma} \int_{-\infty }^{\infty} (x-\mu)^2 \exp\left(- \dfrac{(x-\mu)^2}{2 \sigma^2}\right) \d x\\ &= \dfrac{\sigma^2}{\sqrt{2 \pi}} \int_{-\infty }^{\infty} y^2 \exp(-\tfrac{y^2}{2}) \d y\\ &= \dfrac{\sigma^2}{\sqrt{2 \pi}}\left(- y \exp\left(-\tfrac{y^2}{2}\right)\right)\as_{-\infty}^{\infty} + \sigma^2 \int_{-\infty }^{\infty} \dfrac{1}{\sqrt{2 \pi}} \exp(-\tfrac{y^2}{2}) \d y\\ &= \sigma^2 \end{aligned}$$

对于正态分布 $X \sim \mathcal{N}(\mu, \sigma^2)$，有期望

$$\boxed{ \mathbb{E}[X] = \mu }$$

与方差

$$\boxed{ \operatorname{Var} [X] = \sigma^2 }$$

线性变换

若 $X \sim \mathcal{N}(\mu, \sigma^2)$，则对任意常数 $a \ne 0, b$，有随机变量

$$Y = a X + b \sim \mathcal{N}(a \mu + b, a^2 \sigma^2)$$

证明

假设 $a > 0$，则有

$$\begin{aligned} F_Y(y) &= \Pr(Y \le y)\\ &= \Pr\left(X \le \tfrac{y-b}{a}\right)\\ &= F_X\left(\tfrac{y-b}{a}\right)\\ \end{aligned}$$

链式法则有

$$\begin{aligned} f_Y(y) &= \dfrac{\d F_Y(y)}{\d y}\\ &= \dfrac{1}{a} f_X\left(\tfrac{y-b}{a}\right) \end{aligned}$$

同理可得 $a < 0$ 时的情况，综合有

$$f_Y(y) = \dfrac{1}{|a|} f_X\left(\tfrac{y-b}{a}\right) = \dfrac{1}{\sqrt{2\pi} |a| \sigma} \exp\left(-\dfrac{(y - a\mu - b)^2}{2a^2 \sigma^2}\right)$$

也就是说，若 $X \sim \mathcal{N}(\mu, \sigma^2)$，那么有 $\dfrac{X - \mu}{\sigma} \sim \mathcal{N}(0, 1)$，也就是说可以将随机变量进行标准化。

反过来也有若 $X \sim \mathcal{N}(0, 1)$，则 $\sigma X + \mu \sim \mathcal{N}(\mu, \sigma^2)$。

卷积（Convolution）

密度函数 $f_X, f_Y$ 的卷积（convolution）$f_X * f_Y$ 定义为

$$\begin{aligned} f_X * f_Y (z) &= \int_{-\infty}^{\infty} f_X(x) f_Y(z - x) \d x\\ &= \int_{-\infty}^{\infty} f_X(z - y) f_Y(y) \d y \end{aligned}$$

若连续随机变量 $X, Y$ 独立，则有 $f_{X+Y} = f_X * f_Y$。

证明

有 $F_{X+Y}(z)$ 为

$$\begin{aligned} \Pr(X + Y \le z) &= \iint_{u + v \le z} f_X(u) f_Y(v) \d u \d v\\ &= \int_{u=-\infty }^{\infty }\int_{v=-\infty }^{z-u} f_X(u) f_Y(v) \d v \d u\\ &= \int_{x=-\infty }^{\infty } f_X(x) \int_{y=-\infty }^{z} f_Y(y-x) \d y \d x \end{aligned}$$

从而

$$\begin{aligned} f_{X+Y}(z) &= \dfrac{\d F_{X+Y}(z)}{\d z}\\ &= \int_{-\infty }^{\infty } f_X(x) f_Y(z-x) \d x\\ &= f_X * f_Y(z) \end{aligned}$$

若随机变量 $X \sim \mathcal{N}(\mu, \sigma^2),\, Y \sim \mathcal{N}(\nu, \tau^2)$ 独立，则

$$X + Y \sim \mathcal{N}(\mu + \nu, \sigma^2 + \tau^2)$$

证明

使用卷积即可，过程比较繁琐，略。

标准正态分布

若有服从标准正态分布的随机变量 $X \sim \mathcal{N}(0, 1)$，则其概率密度函数 pdf

$$\boxed{\varphi(x) = \dfrac{1}{\sqrt{2 \pi}} \exp\left(-\tfrac{x^2}{2}\right)}$$

若有标准正态分布的随机变量 $X \sim \mathcal{N}(0, 1)$，则其累积分布函数 CDF

$$\begin{aligned} \Phi(z) = \Pr(X \le z) &= \int_{-\infty }^z \dfrac{1}{\sqrt{2 \pi}} \exp\left(-\tfrac{x^2}{2}\right) \d x\\ &= \dfrac{1}{2} + \dfrac{1}{2} \operatorname{erf}\left(\dfrac{z}{\sqrt{2}}\right) \end{aligned}$$

$\Phi(z)$ 没有一个简单的解析形式（no closed-form expression），但是可以通过数值积分得到。

其中定义误差函数（error function）

$$\operatorname{erf}(z) = \dfrac{2}{\sqrt{\pi}} \int_{0}^{z} \exp(-t^2) \d t$$

根据对称性，有 $\Phi(-z) = 1 - \Phi(z)$。

对于一般的正态分布，$X \sim \mathcal{N}(\mu, \sigma^2)$，有

$$\Pr(X \le x) = \Phi\left(\dfrac{x - \mu}{\sigma}\right)$$

矩生成函数（矩母函数，Moment Generating Function）

随机变量 $X$ 的矩生成函数（moment generating function, MGF）定义为

$$M_X(t) = \mathbb{E}[\e^{tX}]$$

可根据麦克劳林级数展开得到

$$M_X(t) = \sum_{k \ge 0} \dfrac{t^k \mathbb{E}[X^k]}{k!}$$

因此第 $k$ 阶矩为 $\mathbb{E}[X^{k}] = M_X^{(k)}(0)$。

若对于一些 $\delta > 0$ 有，$M_X(t) = M_Y(t)$ 对于任意 $t \in [- \delta, \delta]$ 恒成立，则 $X, Y$ 同分布。

标准正态分布 $X \sim \mathcal{N}(0, 1)$ 的 MGF 为

$$M_X(t) = \exp\left(\tfrac{t^2}{2}\right)$$

证明

$$\begin{aligned} M_X(t) &= \mathbb{E}[\e^{t X}]\\ &= \dfrac{1}{\sqrt{2 \pi}} \int_{-\infty }^{\infty} \exp\left(-\tfrac{x^2}{2} + tx\right) \d x\\ &= \dfrac{1}{\sqrt{ 2 \pi}} \int_{-\infty }^{\infty} \exp\left(-\tfrac{(x-t)^2}{2} + \tfrac{t^2}{2}\right) \d x\\ &= \dfrac{1}{\sqrt{2 \pi}} \exp\left(\tfrac{t^2}{2}\right) \int_{-\infty }^{\infty} \exp\left(-\tfrac{(x-t)^2}{2}\right) \d x\\ &= \exp\left(\tfrac{t^2}{2}\right) \end{aligned}$$

Large Deviation (Concentration) Bound

若 $X \sim \mathcal{N}(\mu, \sigma^2)$，则对任意 $a > 0$ 有

$$\Pr(|X - \mu| \ge a \sigma) \le 2 \exp\left(-\frac{a^2}{2}\right)$$

证明

考虑标准化 $Z = \dfrac{X - \mu}{\sigma} \sim \mathcal{N}(0, 1)$.

上尾（upper tail）有

$$\begin{aligned} \Pr(X - \mu \ge a \sigma) &= \Pr(Z \ge a)\\ &= \Pr(\e^{t Z} \ge \e^{t a})\\ &\le \dfrac{\mathbb{E}[\e^{t Z}]}{\e^{t a}}\\ &= \exp\left(\tfrac{t^2}{2} - a t\right)\\ &\le \exp\left(-\tfrac{a^2}{2}\right) \end{aligned}$$

最后一步取 $t = a$ 是因为此时可以使得 $\exp\left( \tfrac{t^2}{2} - ta \right)$ 最小。

下尾（lower tail）$\Pr(X - \mu \le -a \sigma) = \Pr(Z \le -a)$ 根据对称性也有同样的结论。

68-95-99.7 法则：

二元正态分布（Bivariate Normal Distribution）

以 $\rho \in (-1, 1)$ 为参数的标准二元正态随机变量 $(X, Y)$ 的联合密度函数为

$$f_{X, Y}(x, y) = \dfrac{1}{2\pi \sqrt{1 - \rho^2}} \exp\left(-\dfrac{1}{2(1 - \rho^2)}(x^2 - 2\rho x y + y^2)\right)$$

$X, Y$ 的边缘分布均为标准正态分布 $\mathcal{N}(0, 1)$，同时有

$$\begin{aligned} \operatorname{Cov}(X, Y) &= \mathbb{E}[XY] - \mathbb{E}[X] \mathbb{E}[Y]\\ &= \int_{-\infty }^{\infty }\int_{-\infty }^{\infty }xy f_{X, Y}(x, y) \d x \d y\\ &= \rho \end{aligned}$$

因此，$\rho = 0$ 可以得到 $f_{X, Y}(x, y) = \varphi(x) \varphi(y)$。

也就是说，标准二元正态随机变量相互独立，当且仅当他们无关（相关系数为 0）。

「独立」$\implies$「不相关」，但标准二元正态随机变量「独立」$\iff$「不相关」。

对于一般的二元正态随机变量 $(X, Y)$，其中其均值分别为 $\mu_1, \mu_2$，方差分别为 $\sigma_1^2, \sigma_2^2$，相关系数为 $\rho$，它的联合密度函数为

$$f_{X, Y}(x, y) = \dfrac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1 - \rho^2}} \exp\left( -\tfrac{1}{2} Q(x, y) \right)$$

其中

$$Q(x, y) = (x - \mu_1, y - \mu_2) \begin{bmatrix} \sigma_1^2 & \sigma_1 \sigma_2 \rho \\ \sigma_1 \sigma_2 \rho & \sigma_2^2 \end{bmatrix}^{-1} (x - \mu_1, y - \mu_2)^\intercal$$

边缘分布有 $X \sim \mathcal{N}(\mu_1, \sigma_1^2),\, Y \sim \mathcal{N}(\mu_2, \sigma_2^2)$，同时协方差 $\operatorname{Cov}(X, Y) = \sigma_1 \sigma_2 \rho$。

中间的矩阵就是协方差矩阵 $\Sigma$ 的逆矩阵。

多元正态分布（Multivariate Normal Distribution）*

随机向量 $\mathbf{Y} = (Y_1, \cdots, Y_n)$ 有着多元正态分布，当且仅当存在矩阵 $\bm{A} \in \R^{n \times k}$ 与 $k$ 个独立的标准正态随机变量的向量 $\mathbf{X} = (X_1, \cdots, X_k)$ 与向量 $\bm{\mu} = (\mu_1, \cdots, \mu_n) \in \R^n$ 使得

$$\mathbf{Y}^\intercal = \bm{A} \mathbf{X}^\intercal + \bm{\mu}^\intercal$$

若更进一步的，协方差矩阵 $\bm{\Sigma} = \bm{A} \bm{A}^\intercal = \mathbb{E}[(\mathbf{Y} - \bm{\mu})(\mathbf{Y} - \bm{\mu})^\intercal]$ 满秩，则 $\mathbf{Y}$ 的密度函数为

$$f(\bm{y}) = f(y_1, \dots, y_n) = \dfrac{1}{\sqrt{(2 \pi)^n \det(\bm{\Sigma})}}\exp\left( -\tfrac{1}{2}(\bm{y} - \bm{\mu}) \bm{\Sigma}^{-1} (\bm{y} - \bm{\mu})^\intercal \right)$$

表示为 $\mathbf{Y} \sim \mathcal{N}(\bm{\mu}, \bm{\Sigma})$。

边缘分布有 $Y_i \sim \mathcal{N}(\mu_i, \Sigma_{ii})$ 与 $\operatorname{Cov}(Y_i, Y_{j}) = \Sigma_{ij}$。

对任意 $\bm{a} \in \R^n$，有 $\left\langle \bm{a}, \mathbf{Y} \right\rangle = a_1 Y_1 + \dots + a_n Y_n$ 也服从正态分布。

其他连续概率分布

卡方分布（Chi-Squared Distribution）*

若 $Z_1, \dots, Z_k$ 是 $k$ 个独立的标准正态分布随机变量，则随机变量

$$Q = \sum_{i=1}^{k} Z_i^2$$

服从 $k$ 个自由度（degrees of freedom）的卡方分布（chi-squared distribution），记作 $Q \sim \chi^2(k)$。

卡方分布有期望

$$\begin{aligned} \mathbb{E}[Q] &= \sum_{i=1}^{k}\mathbb{E}[Z_i^2]\\ &= \sum_{i=1}^{k} \operatorname{Var} [Z_i]\\ &= k \end{aligned}$$

独立的 $\chi^2(k)$ 与 $\chi^2(l)$ 随机变量的和服从 $\chi^2(k+l)$。

令 $Z \sim \mathcal{N}(0, 1)$ 与 $Y = Z^2$，于是对于任意 $y \ge 0$ 有

$$\begin{aligned} F_Y(y) &= \Pr(Y \le y)\\ &= \Pr(Z^2 \le y)\\ &= \Pr(- \sqrt{y} \le Z \le \sqrt{y})\\ &= \Phi(\sqrt{y}) - \Phi(-\sqrt{-y})\\ &= 2 \Phi(\sqrt{y}) - 1 \end{aligned}$$

链式法则有

$$\begin{aligned} f_Y(y) &= \dfrac{\d F_Y(y)}{\d y}\\ &= \dfrac{1}{\sqrt{y}}\varphi(\sqrt{y})\\ &= \dfrac{1}{\sqrt{2 \pi y}} \exp\left(-\tfrac{y}{2}\right) \end{aligned}$$

于是 $\chi^2(1)$ 有 pdf $f(x) = \dfrac{1}{\sqrt{2 \pi x}} \exp(-\tfrac{x}{2})$。

对于更一般的整数 $k \ge 1$，$\chi^2(k)$ 有 pdf $f(x) = \dfrac{1}{2^{k/2} \Gamma(k/2)} x^{k/2 - 1} \exp(-\tfrac{x}{2})$。

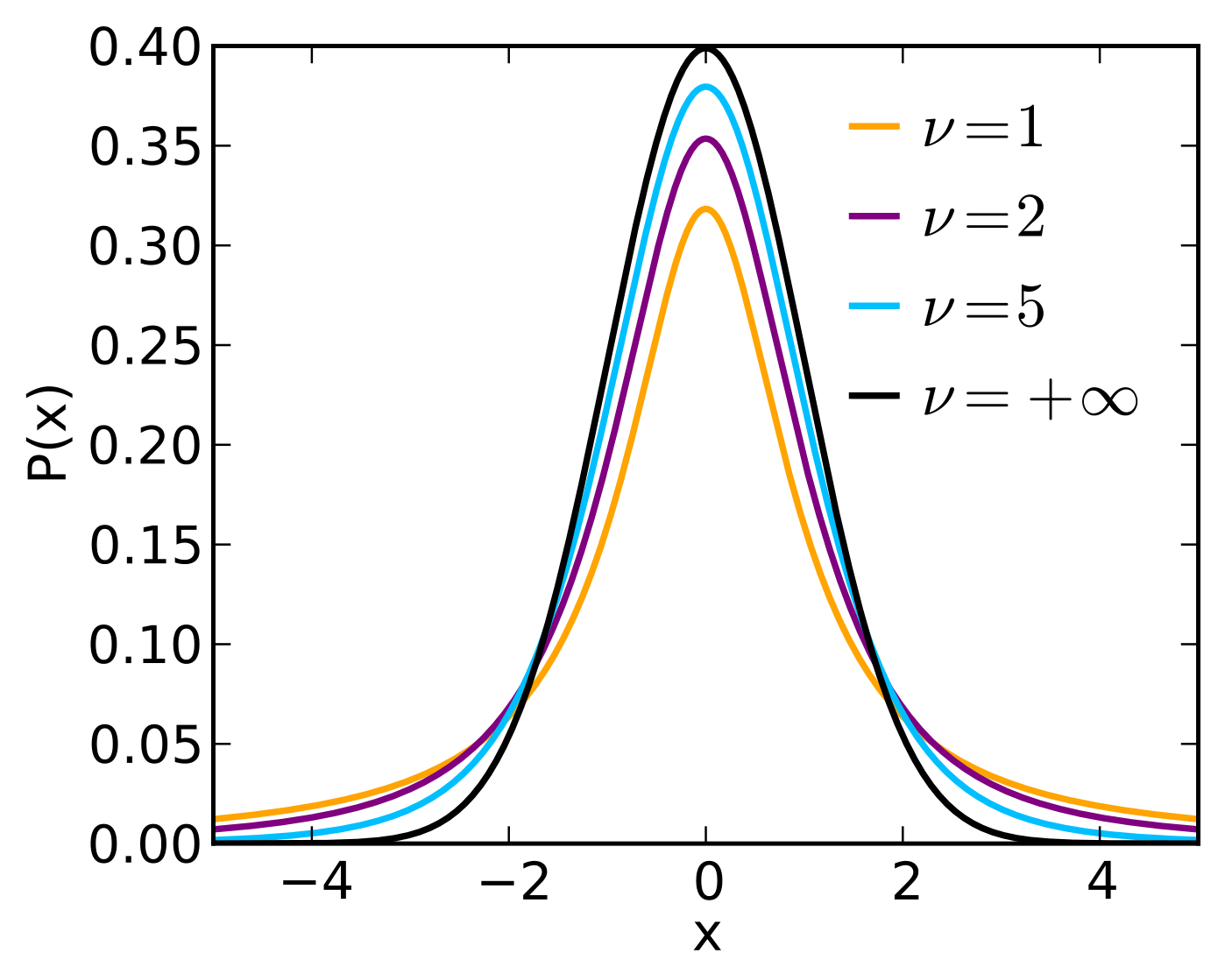
学生 $t$ 分布（Student's $t$ Distribution）*

若随机变量 $X \sim \mathcal{N}(0, 1),\, Y \sim \chi^2(n)$ 独立，则随机变量

$$T = \dfrac{X}{\sqrt{Y/n}}$$

服从 $n$ 个自由度的学生 $t$ 分布（Student's $t$ distribution），记作 $T \sim t(n)$。

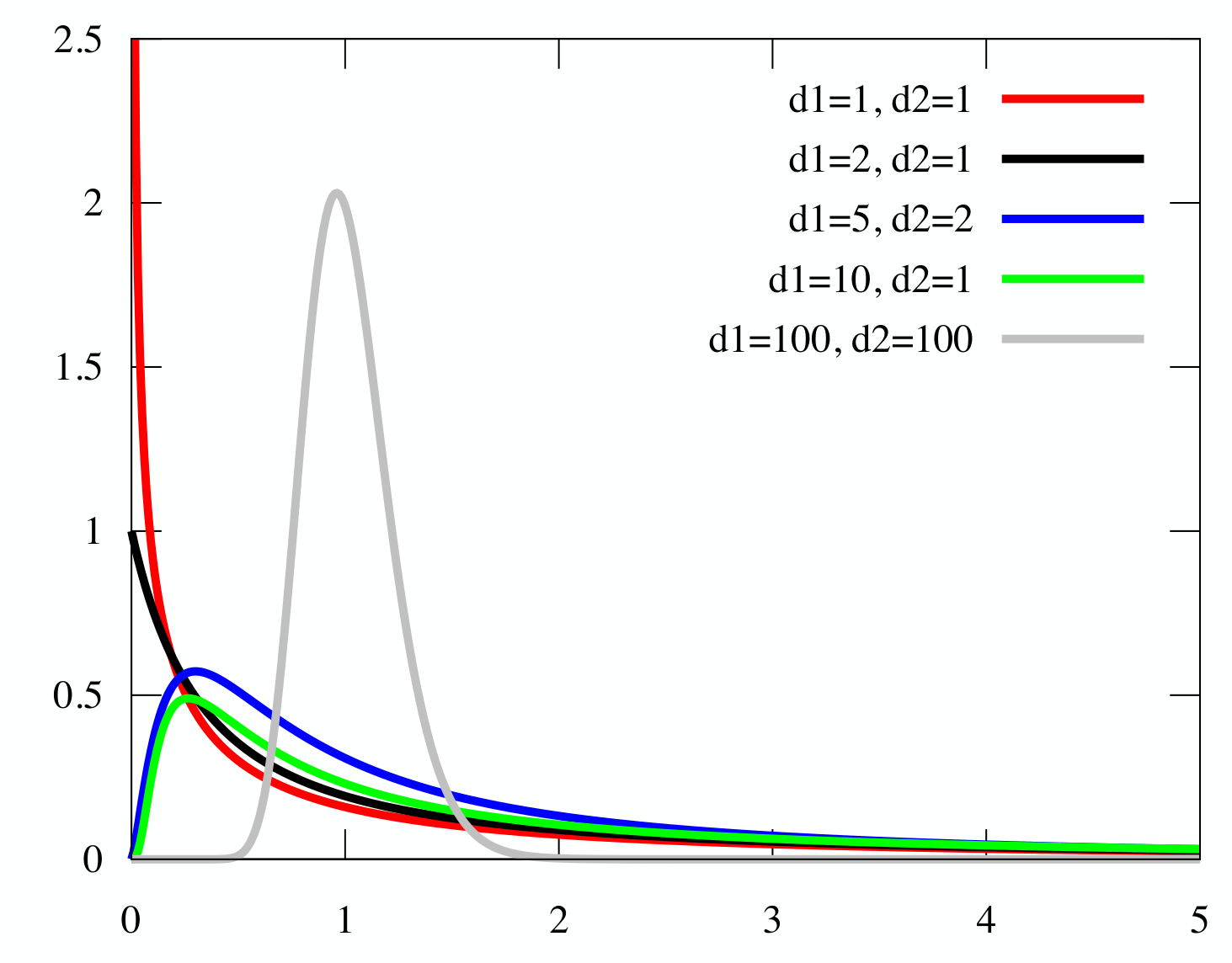
$F$ 分布（F Distribution）*

若随机变量 $X \sim \chi^2(n),\, Y \sim \chi^2(m)$ 独立，则随机变量

$$F = \dfrac{X/n}{Y/m}$$

服从 $n, m$ 个自由度的 $F$ 分布（$F$ distribution），记作 $F \sim F(n, m)$。

伽马分布（Gamma Distribution）*

Gamma 函数

Gamma 函数是阶乘的解析延拓（$\Gamma(n) = (n-1)!$），定义为

$$\Gamma(z) = \int_{0}^{\infty} t^{z-1} \exp(-t) \d t,\quad \Re(z) > 0$$

$\Gamma(1) = \displaystyle \int_0^{\infty }\e^{-t} \d t = 1$ 给出了 $\lambda = 1$ 的指数分布。

而 $\Gamma(k) = \displaystyle \int_0^{\infty } (\lambda t)^{k-1}\lambda \e^{- \lambda t} \d t = \mathbb{E}[(\lambda X)^{k-1}]$ 则是 $\lambda > 0$ 的指数随机变量 $X$。

随机变量 $X$ 服从参数为 $k, \lambda > 0$ 的伽马分布（gamma distribution），记作 $X \sim \Gamma(k, \lambda)$，若其概率密度函数为

$$f_X(x) = \dfrac{1}{\Gamma(k)} \lambda^k x^{k-1} \exp(-\lambda x),\quad x \ge 0$$

• $\Gamma(1, \lambda)$ 是参数为 $\lambda$ 的指数分布。
• $\Gamma(\frac{k}{2}, \frac{1}{2})$ 是参数为 $k$ 的卡方分布，其中 $k \ge 1$ 为整数。
• 若 $X \sim \Gamma(\alpha, \lambda),\, Y \sim \Gamma(\beta, \gamma)$ 独立，则 $X + Y \sim \Gamma(\alpha + \beta, \lambda + \gamma)$。

伽马随机变量 $X \sim \Gamma(k, \lambda)$ 的 MGF 为

$$M_X(t) = \left( 1 - \dfrac{t}{\lambda} \right)^{-k},\quad t < \lambda$$

证明

$$\begin{aligned} M_X(t) &= \mathbb{E}[ \e^{tX} ]\\ &= \int_0^{\infty }\e^{tx} f_X(x) \d x\\ &= \dfrac{\lambda^k}{\Gamma(k)} \int_0^{\infty } x^{k-1} \e^{-(\lambda - t)x} \d x\\ &= \dfrac{\lambda^k}{\Gamma(k)(\lambda - t)^{k}} \int_0^{\infty }u^{k-1}\e^{-u}\d u\\ &= \dfrac{\lambda^k \Gamma(k)}{\Gamma(k)(\lambda - t)^k}\\ &= \left( 1 - \dfrac{t}{\lambda} \right)^{-k} \end{aligned}$$

令 $\left\lbrace N(t) \mid t \ge 0 \right\rbrace$ 是一个参数为 $\lambda$ 的泊松过程，对于任意 $t, s \ge 0$ 与自然数 $n$，有

$$\Pr(N(t + s) - N(t) = n) = \dfrac{(\lambda s)^n}{n!} \e^{-\lambda s}$$

证明

无记忆性有，等价于证明 $\Pr(N(t) = n) = \dfrac{(\lambda t)^n}{n!} \e^{-\lambda t}$。

对于 i.i.d. 以 $\lambda$ 为参数的指数随机变量 $X_i$，有

$$\begin{aligned} \Pr(N(t) = n) &= \Pr\left( \sum_{i=1}^{n}X_i \le t \cap \sum_{i=1}^{n+1} X_i > t \right) \\ &= \int_0^t f_{\sum_{i=1}^nX_i}(x) \cdot \Pr(X_{n+1} > t - x) \d x\\ &= \int_0^t \dfrac{(\lambda x)^{n-1} \lambda \e^{-\lambda x}}{\Gamma(n)} \e^{-\lambda(t-x)} \d x\\ &= \dfrac{\lambda^n \e^{-\lambda t}}{\Gamma(n)} \int_0^t x^{n-1} \d x\\ &= \dfrac{\lambda^n \e^{-\lambda t}t^n}{n \Gamma(n)}\\ &= \e^{-\lambda t} \dfrac{(\lambda t)^n}{n!} \end{aligned}$$

贝塔分布（Beta Distribution）*

随机变量 $X$ 服从参数为 $a, b > 0$ 的贝塔分布（beta distribution），记作 $X \sim \operatorname{Beta}(a, b)$，若其概率密度函数为

$$f_X(x) = \dfrac{1}{B(\alpha, \beta)} x^{\alpha - 1} (1 - x)^{\beta - 1},\quad 0 \le x \le 1$$

其中贝塔函数（beta function）

$$B(a, b) = \dfrac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)} = \int_{0}^{1} t^{a-1} (1 - t)^{b-1} \d t$$

• $\operatorname{Beta}(1, 1)$ 是 $[0, 1]$ 上的均匀分布。
• $\operatorname{Beta}(1, n)$ 是 $\min\limits_{1\le i\le n}X_i$ 的分布，其中 $X_i$ 是独立的 $[0, 1]$ 上的均匀分布。
• 若 $X \sim \Gamma(\alpha, \lambda),\, Y \sim \Gamma(\beta, \lambda)$ 独立，则 $\dfrac{X}{X+Y} \sim \operatorname{Beta}(\alpha, \beta)$。

柯西分布（Cauchy Distribution）*

随机变量 $X$ 服从柯西分布（Cauchy distribution），若其概率密度函数为

$$f_X(x) = \dfrac{1}{\pi(1 + x^2)}$$

柯西随机变量 $X$ 不存在任何矩。即 $\mathbb{E}[X^{k}] = \infty$ 对于任意 $k \ge 1$ 成立。

也就是说其 MGF 不存在。

---

1. 这是 I $\mathscr{I}$ \mathscr{I}，不是 F $\mathscr{F}$ \mathscr{F}。 ↩︎

2. The random variables $X, Y$ are (jointly) continuous with joint (probability) density function $f_{X, Y}\colon \R^2 \to[0, \infty )$ if for all $x, y \in \R$. ↩︎

3. 对任意 $x < 0$，有 $f_X(x) = 0$（连续）或 $p_X(x) = 0$（离散）。还有一个（弱）定义是 $\Pr[X \ge 0] = 1$，即 $X \ge 0$ 几乎必然发生（almost sure）。 ↩︎

4. 可以是 $[a, b],\, (a, b),\, [a, b),\, (a, b]$。 ↩︎

5. $F^{-1}$ gives the quantile of $X$. ↩︎

6. $X$ dominates $Y$ stochastically. ↩︎