平摊分析

之前的笔记中有相关的记录。

Amortized Analysis

Idea: Even when expensive operations must be performed, it is often possible to get away with performing them rarely, so that the average cost per operation is not so high.

Amortized analysis is different from what is commonly referred to as average case analysis, because it does not make any assumption about the distribution of the data values, whereas average case analysis assumes the data are not "bad".

That is, amortized analysis is a worst case analysis, but for a sequence of operations, rather than for individual operations.

Aggregate method for Amortized Analysis

One assumes that there is no need to distinguish between the different operations on the data structure.

We just use aggregate method: Add up the cost of all the operations and then divide by the number of operations.

$$\text{aggregate cost} = \dfrac{\text{max amount of work done by any series of $m$ operations}}{m}$$

Let $N = 2^{k}$ for some constant $k$. Then maximum copying cost of $N$ insertions in CircularArray is $1 + 2 + \dots + 2^{k-1} = 2^{k} - 1 \approx N$.

Therefore, the aggregate cost is $O\left(\frac{N + N}{N}\right) = O(1)$.

Definition

Note: Different operations may have different amortized costs.

Operation has amortized cost $\hat{c}(n)$ if for every $k \in \N^{+}$, the total cost of any $k$ operations is at most $\displaystyle \sum_{i=1}^n \hat{c}(n_i)$, where $n_i$ is the size of the data structure when applying the $i$-th operation.

Consider a sequence operations:

• $c_i$ is the actual cost of the $i$-th operation
• $\hat{c}_i$ is the amortized cost of the $i$-th operation

For the amortized cost to be valid:

$$\sum_{i=1}^{k} c_i \le \sum_{i=1}^{k} \hat{c}_i\quad \forall k \in \N^{+}$$

• Total cost of $k$ operations $\le \displaystyle \sum_{i=1}^{k} \hat{c}_i$
• Average cost of $k$ operations $\le \dfrac{\displaystyle \sum_{i=1}^{k}\hat{c}_i}{k}$

Example: Consider CircularArray implementation of Queue

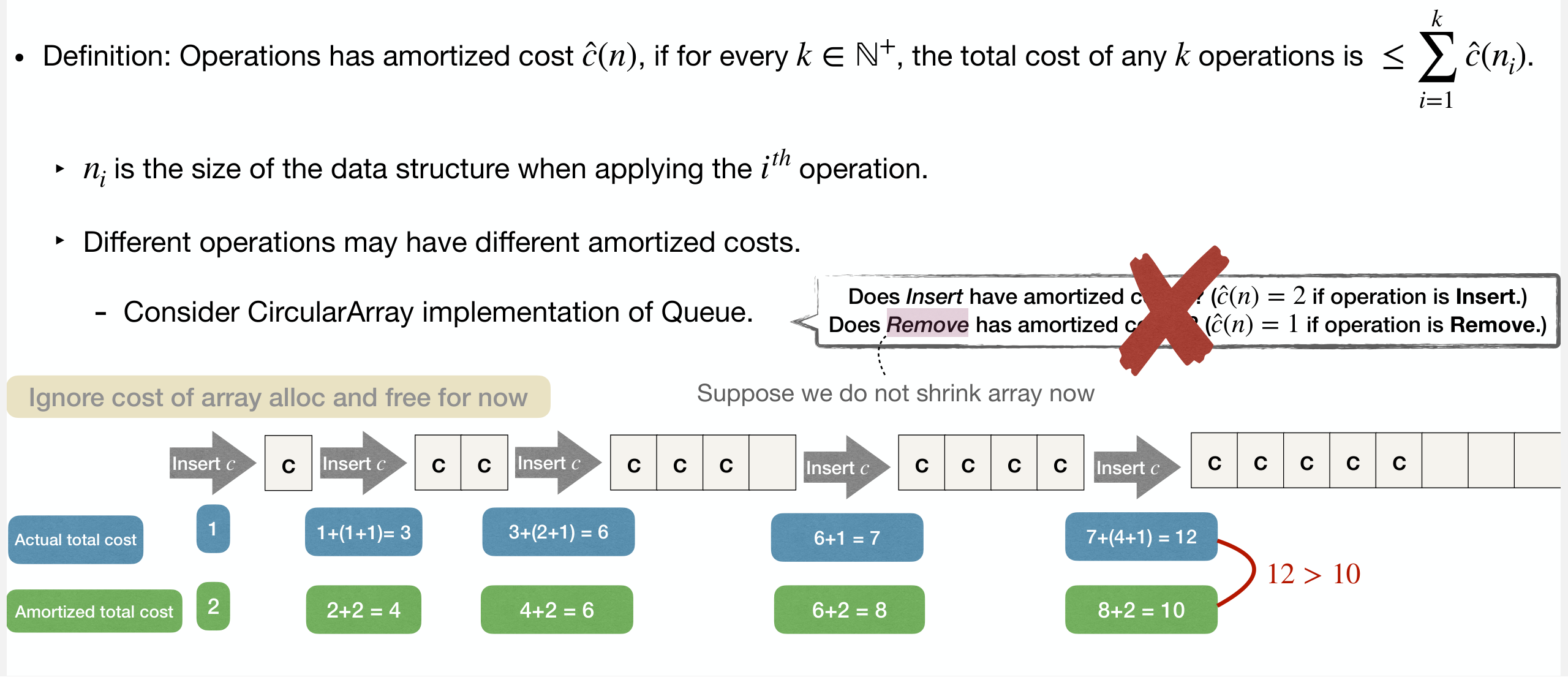
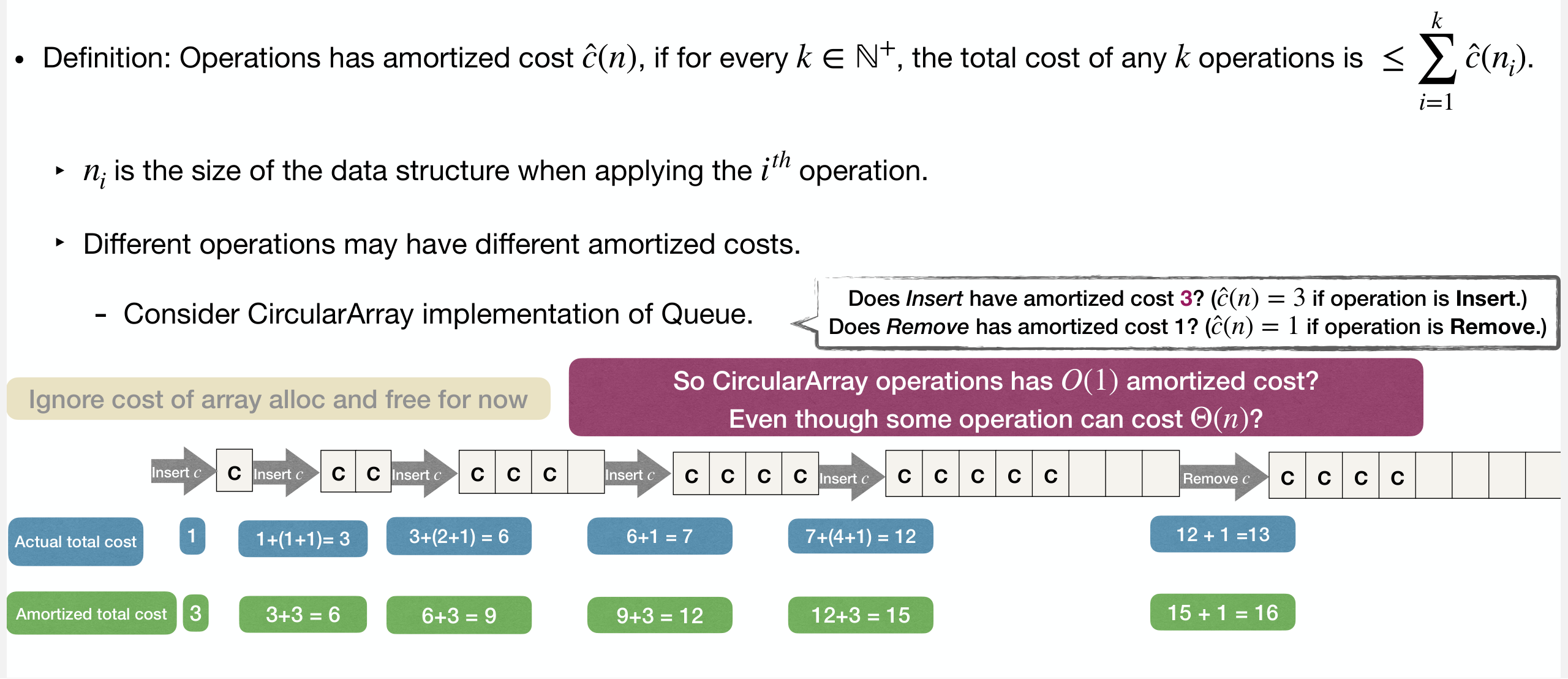
It is not enough to prove using just 6 operations.

Amortized Analysis Techniques

The Accounting Method(记账法)

Imagine you have a bank account $B$ with initial balance $0$.

For the $i$-th operation, you spend $\hat{c}_i$ money:

• Recall that the actual cost of the $i$-th operation is $c_i$
• If $\hat{c}_i \ge c_i$, pay $c_i$ for the operation and deposit $\hat{c}_i - c_i$ into $B$.
• If $\hat{c}_i < c_i$, pay $\hat{c}_i$ for the operation and withdraw $c_i - \hat{c}_i$ from $B$.

Amortized analysis valid if

$$B = \sum_{i=1}^{k}(\hat{c}_i - c_i)$$

always $\ge 0$ for all $k$.

Example: Queue with CircularArray

$\hat{c}_i = 3$ if the $i$-th operation is Insert and $\hat{c}_i = 1$ if the $i$-th operation is Remove.

• Goal: Prove $\displaystyle \sum_{i=1}^{k}c_i \le \sum_{i=1}^{k}\hat{c}_i$ for any $k \in \N^{*}$ operations.
• Strategy: account always non-negative via induction on $k$.
• Basis: Prior to 1st operation, account balance is $0$.
• Hypothesis: Prior to $i$-th operation, account balance is always non-negative.

Inductive Step: Consider the $i$-th operation

• If it's Remove, then we make no change to account value.
• $\hat{c}_i - c_i = 1 - 1 = 0$
• If it's Insert without expansion, we add $2$ to account value.
• $\hat{c}_i - c_i = 3 - 1 = 2$
• If it's Insert with expansion. Assume expand from $n$ to $2n$, then we need to withdraw $n - 1$ value.
• $c_i - \hat{c}_i = n + 1 - 2 = n - 1$
• Analysisstep:

1. Last expand must be from $\dfrac{n}{2}$ to $n$.
2. Since last expand, each Insert adds $2$ and each Remove makes no change.
3. Since last expand, there are at least $\dfrac{n}{2}$ Insert operation.
4. Account balance is at least $\dfrac{n}{2} \times 2 = n$.
5. After the $i$-th operation, account balance is at least $n - (n - 1) = 1$.
6. Account balance is always non-negative.

Example: Binary Counter

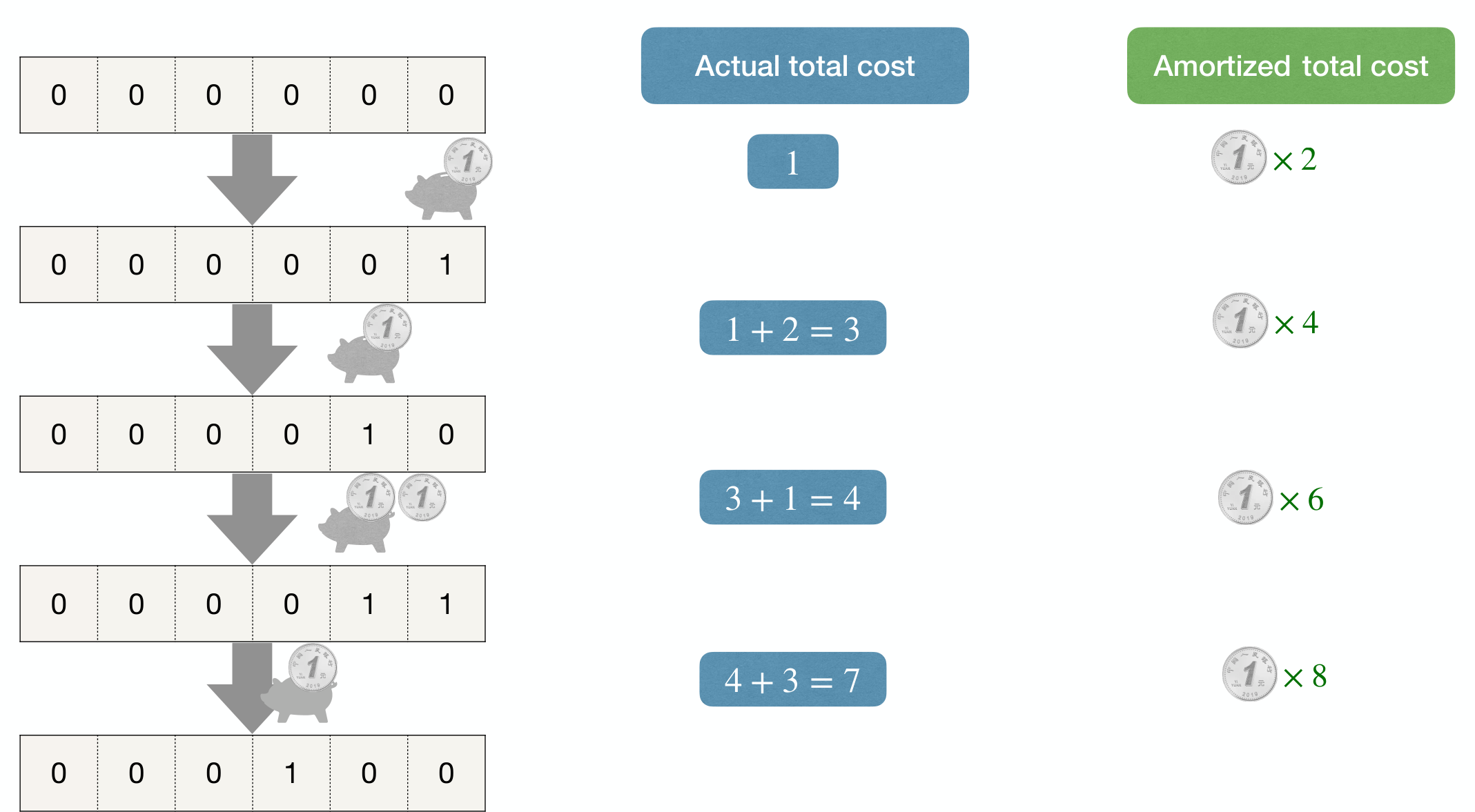
The disadvantage of the accounting method is that it is not always easy to find the right accounting scheme. The guess is always constant.

The Potential Method(势能法)

Design a potential function $\Phi$ that maps data structure status to real values:

• $\Phi(D_0)$: Initial potential of the data structure, usually set to $0$.
• $\Phi(D_i)$: Potential of the data structure after $i$-th operation.

Define

$$\hat{c}_i = c_i + \Phi(D_i) - \Phi(D_{i-1})$$

Amortized analysis valid if

$$\Phi(D_{k}) \ge \Phi(D_0)$$

for all $k$.

Potential is like the balance in account in Counting Method.

• Potential slowly accumulates during cheap operations (deposit).
• Potential is used to pay for expensive operations (withdraw).

Example: Binary Counter

The last line is because, in one operation, it will turn $0$ to $1$ at most $1$ time.