散列表

Hashing

SIR in $O(1)$ time

Efficient implementation for ORDERED DICTIONARY:

	Search(S, k)	Insert(S, x)	Remove(S, x)
BinarySearchTree	$O(h)$ in worst case	$O(h)$ in worst case	$O(h)$ in worst case
Treap	$O(\log n)$ in expectation	$O(\log n)$ in expectation	$O(\log n)$ in expectation
RB-Tree	$O(\log n)$ in worst case	$O(\log n)$ in worst case	$O(\log n)$ in worst case
SkipList	$O(\log n)$ in expectation	$O(\log n)$ in expectation	$O(\log n)$ in expectation

If we only care about Search, Insert and Remove operation, can we be faster?

Assuming keys are distinct integers from universe $U = \left\lbrace 1, 2, \cdots, m-1 \right\rbrace$. Just allocate an array of size $m = |U|$ and Search, Insert and Remove can be done in $O(1)$ time.

Problem: What if keys are not integers, e.g., strings?

The real problem is that the universe $U$ can be very large. Sometime the space complexity is unacceptable.

Hash function

We are given huge universe $U$ of possible keys and much smaller number $n$ of actual keys. And we only want to spend $m \approx n$ (i.e., $m \ll |U|$) space, meanwhile supporting very fast SIR.

Hash function(散列函数/哈希函数) $h\colon U \to [m]$ maps keys from universe $U$ to buckets of a hash table $T[0 \cdots m-1]$.

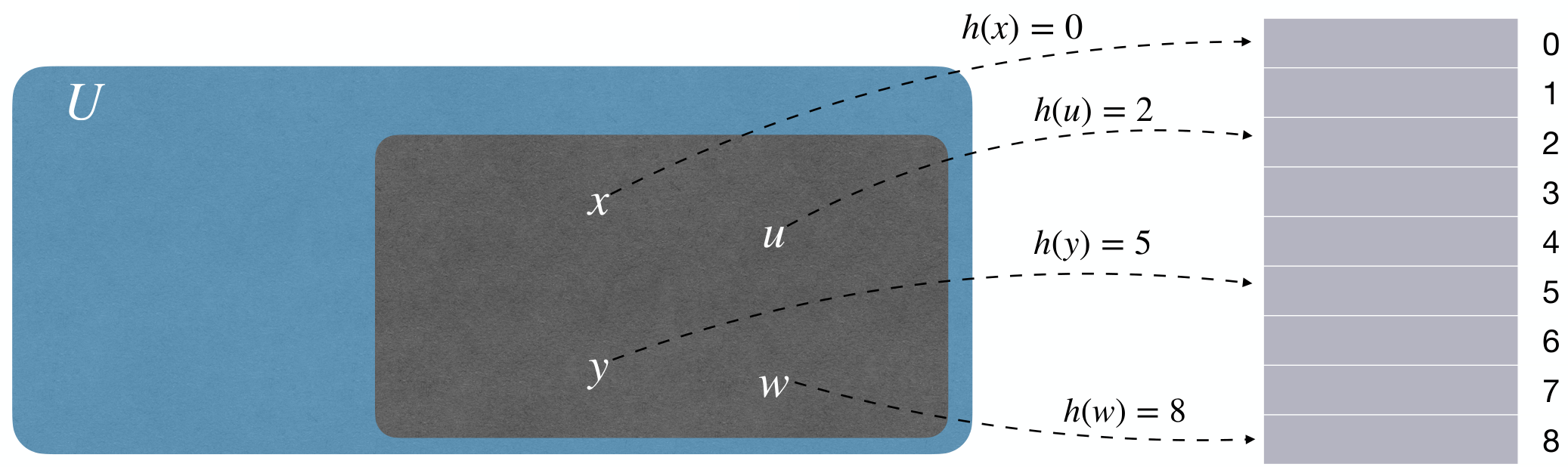
The time complexity of hash function should be $O(1)$ for every key.

And we want to avoid collisions. That is, we want $h$ maps distinct keys to distinct indices.

Two distinct keys $k_1, k_2$ collide(冲突) if $h(k_1) = h(k_2)$.

However this is impossible cos $m \ll |U|$(pigeonhole principle). Therefore, collisions are unavoidable and we have to cope with them.

Hashing with Chaining

Chaining(链接法) is a simple way to resolve collisions. We store all the keys that hash to the same bucket in a LINKEDLIST.

Each bucket $i$ stores a pointer to a LINKEDLIST $L_i$ and all keys that are hashed to index $i$ go to $L_i$.

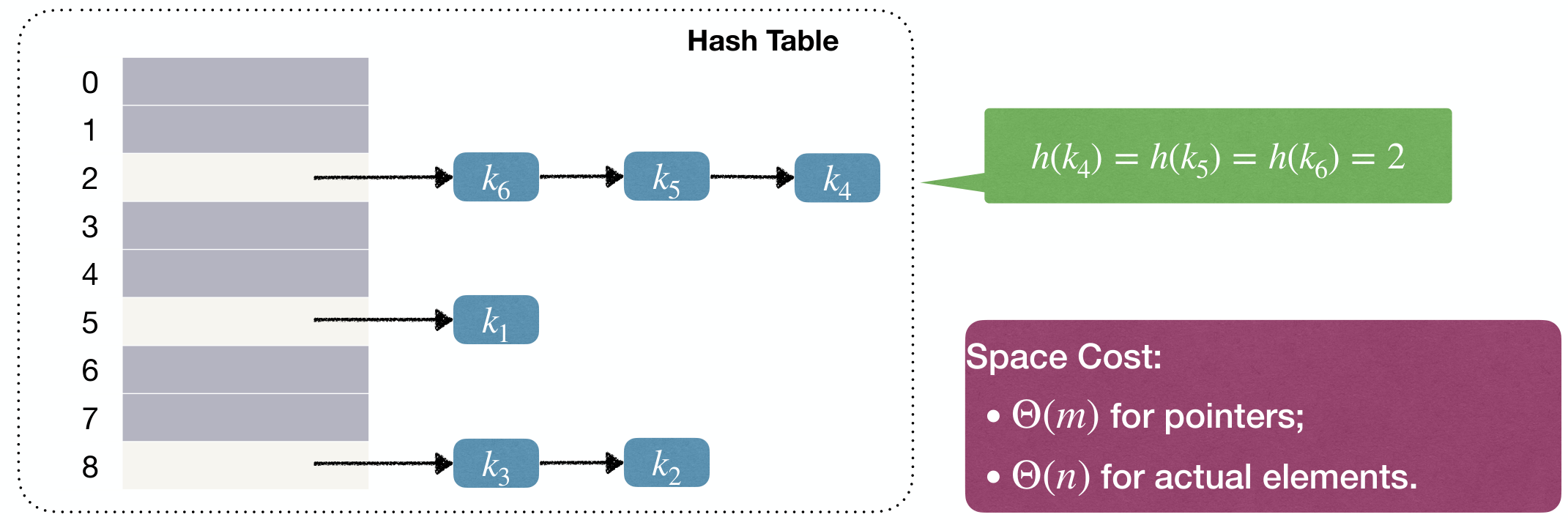
Space Cost:

• $\Theta(m)$ for pointers;
• $\Theta(n)$ for actual elements.

Operation:

• Search(k): where k is a key.
  • Compute h(k) and go through the corresponding list to search item with key k.
• Insert(x): where x is a pointer to an item.
  • Compute h(x.key) and insert x to the head of the corresponding list.
• Remove(x): where x is a pointer to an item.
  • Simply remove x from the LINKEDLIST.

Search can cost $\Theta(n)$ in worst-case if all keys hash to the same bucket. At this time, the hashing table with chaining degrades to a LINKEDLIST.

Performance

Simple Uniform Hashing Assumption

• Every key is equally likely to map to every bucket.
• Keys are mapped independently.

Each key goes to a randomly chosen bucket, if there are enough number of buckets, each bucket will not have too many keys.

Consider a hash table containing $m$ buckets and storing $n$ keys.

Define load factor(负载因子) $\alpha = \dfrac{n}{m}$.

Intuitively, Search will on average cost $O(1 + \alpha)$ time. $O(1)$ for computing hash value and $O(\alpha)$ for traversing the LINKEDLIST.

Expected cost of unsuccessful search is $\Theta(1 + \alpha)$. The cost is the sum of computing hash value and traversing the entire LINKEDLIST in a bucket.

Expected cost of successful search is $\Theta(1 + \alpha)$ too. The cost is the sum of computing hash value and traversing LINKEDLIST in a bucket till key found.

Let $C_i$ be the cost for finding the $i$-th inserted element $x_i$. We want to compute $\displaystyle \dfrac{1}{n} \sum_{i=1}^{n} \mathbb{E}[C_i]$.

Let $X_{ij}$ be an IRV taking value 1 if and only if h(x_i.key) = h(x_j.key).

$$\begin{aligned} \dfrac{1}{n} \sum_{i=1}^{n} \mathbb{E}[C_i] &= \dfrac{1}{n}\mathbb{E}\left[ 1 + \sum_{j=i+1}^{n}X_{ij} \right] \\ &= \dfrac{1}{n} \sum_{i=1}^{n} \left( 1 + \sum_{j=i+1}^{n} \mathbb{E}[X_{ij}] \right)\\ &= \dfrac{1}{n} \sum_{i=1}^{n} \left( 1 + \sum_{j=i+1}^{n}\dfrac{1}{m} \right)\\ &= \dfrac{1}{n} \sum_{i=1}^{n} \left( 1 + \dfrac{n-i}{m} \right)\\ &= \dfrac{1}{n} \left(n + \dfrac{n(n-1)}{2m}\right)\\ &= 1 + \dfrac{\alpha}{2} - \dfrac{\alpha}{2 n}\\ &= \Theta(1 + \alpha) \end{aligned}$$

So, what is the expected maximum cost for Search? That is, the expected length of the longest LINKEDLIST. This is equivalent to the Max-Load problem(balls into bins problem)

If $m = \Theta(n)$, the answer is $\Theta\left(\frac{\log n}{\log n \log n}\right)$.

Here's a hand wavy proof in Stack Overflow: Maximum load when placing N balls in N bins.

However SUH doesn't hold. Keys are not that random (they usually have patterns). Patterns in keys can induce patterns in hash functions.

And once $h$ is fixed and known, we can find a set of bad keys that hash to same value.

Designs of Hash function

Some bad hash functions

Assume keys are English words.

One bucket for each letter (i.e., 26 buckets). A hash function $h(w)$ is the first letter of the word $w$. This is not uniform since words starting with 'a' are more common than words starting with 'z'.

One bucket for each number in $[26 \times 50]$. Another hash function $h(w)$ is the sum of indices of letters in $w$. This is not uniform since most of words are short words.

The Division Method

This is a common technique when designing hash functions.

Hash function

$$h(k) = k \bmod m$$

Two keys $k_1, k_2$ collide if $k_1 \equiv k_2 \pmod m$.

The key is to pick appropriate $m$.

Say we want to store $n$ keys.

Here's an idea: Let $r = \left\lceil \lg n \right\rceil$ and set $m = 2^r$. Then computing $h(k)$ is very fast: h(k) = k - ((k >> r) << r).

But we only use rightmost $r$ bits of the input key. For example, if all input keys are even, we use at most half space.

In general, we want $m$ to be a prime number.

Assume $m$ to be a composite number and key $k$ and $m$ have common divisor $d$. $h(k)$ is also divisible by $d$ since $(k \bmod m) + \left\lfloor \dfrac{k}{m} \right\rfloor \cdot m = k$. If all input keys are divisible by $d$, we use at most $\dfrac{1}{d}$ space.

Rule of thumb(经验法则)

Pick $m$ to be a prime number not too close to a power of $2$ (or $10$).

The Multiplication Method

Here's another common technique.

Assume key length is at most $w$ bits. Fix table size $m = 2^r$ for some $r \le w$. Fix constant $0 < A < 2^w$.

Hash function

$$h(k) = (Ak \bmod 2^w) \gg (w-r)$$

This is faster than the Division Method, cos Multiplication ant bit-shifting are faster than division.

Universal Hashing(全域散列)

However, once hash function $h$ is fixed and known, there must exist a set of bad keys that hash to the same value. Such adversarial input will result in poor performance.

The solution is to use randomization.

Pick a random hash function $h$ when the hash table is first built. Once chosen, $h$ is fixed throughout entire execution. Since $h$ is randomly chosen, no input is always bad.

A collection of hash functions $\mathscr{H}$ is universal if for any distinct keys $x \ne y$, at most $\dfrac{|\mathscr{H}|}{m}$ hash functions in $\mathscr{H}$ lead to $h(x) = h(y)$. Therefore $\Pr\limits_{h \in \mathscr{H}}[h(x) = h(y)] \le \dfrac{1}{m}$ for all $x \ne y$.

Source of uncertainty:

• SUH: randomness of input.
• Universal Hashing: choice of function $h$ (and potentially randomness of input).

Performance of hashing with chaining

Let $L_{h(k)}$ be the length of list at index $h(k)$, and we want to compute $\mathbb{E}[L_{h(k)}]$.

Claims:

1. If key $k$ is not in table $T$, then $\mathbb{E}[L_{h(k)}] \le \alpha$.
   • For any key $l$, define IRV $X_{kl}$ taking value 1 if and only if $h(k) = h(l)$. Then we have

   $$\begin{aligned} \mathbb{E}[L_{h(k)}] &= \mathbb{E}\left[ \sum_{l \in T, l \ne k} X_{kl} \right] \\ &= \sum_{l \in T, l \ne k} \mathbb{E}[X_{kl}] \\ &\le n \cdot \dfrac{1}{m}\\ &= \alpha \end{aligned}$$

2. If key $k$ is is table $T$, then $\mathbb{E}[L_{h(k)}] \le 1 + \alpha$.
   • We have

   $$\begin{aligned} \mathbb{E}[L_{h(k)}] &= 1 + \mathbb{E}\left[ \sum_{l \in T, l \ne k} X_{kl} \right] \\ &\le 1 + (n-1) \cdot \dfrac{1}{m}\\ &< 1 + \alpha \end{aligned}$$

If the hash table is not overloaded, i.e., $\alpha = O(1)$, SIR can be done in $O(1)$ expected time.

Typical Universal Hash Family

Proposed by Carter and Wegman in 1977.

Find a large prime $p$ larger than the max possible key value.

Let $\Z_p = [p-1] = \left\lbrace 0, 1, \dots, p - 1 \right\rbrace$ and $\Z_p^{*} = \left\lbrace 1, 2, \dots, p - 1 \right\rbrace$.

Define $h_{ab}(k) = ((ak + b) \bmod p) \bmod m$, then

$$\mathscr{H}_{pm} = \left\lbrace h_{ab} \mid a \in \Z_p^{*}, b \in \Z_p \right\rbrace$$

is a universal hash family.

We want to prove that, for all $k \ne l$, $\Pr\limits_{h \in \mathscr{H}_{pm}}[h(k) = h(l)] \le \dfrac{1}{m}$, where $k, l \in \Z_p$.

Let $r = (ak + b) \bmod p, s = (al + b) \bmod p$.

Claim 1

$$r \ne s$$

Proof.

We have $r - s \equiv a(k-l) \pmod p$. However $a \not\equiv 0 \pmod p$ and $k - l \not\equiv 0 \pmod p$, since $p$ is a prime.

So $r - s \ne 0$.

Claim 2

Fix $k, l$, there is a 1-to-1 mapping between $(a, b)$ and $(r, s)$ pairs.

Proof.

这里涉及了「模乘法的逆」的概念，可回看《离散数学》笔记。

Recall $r - s \equiv a(k-l) \pmod p$, then we get $a = (r-s)(k-l)^{-1} \bmod p$ and $b = (r - ak) \bmod p$. $(k-l)^{-1}$ is the modular multiplicative inverse of $k-l$ and it is unique since $p$ is a prime.

$$\begin{aligned} r - s \equiv a(k-l) \pmod p &\iff a \equiv (r-s)(k-l)^{-1} \pmod p \\ &\iff a = (r-s)(k-l)^{-1} \bmod p \end{aligned}$$

Then we get unique $(a, b)$ given distinct $(r, s)$.

There are $p(p-1)$ pairs of $(r, s)$ and $p(p-1)$ pairs of $(a, b)$. As a result, there is a 1-to-1 mapping between $(a, b)$ and $(r, s)$ pairs.

Thus, for any given pair of distinct inputs of $k, l$, if we pick $(a, b)$ uniformly at random from $\Z^{*} \times \Z_p$, the resulting pair $(r, s)$ is equally likely to be any pair of distinct values modulo $p$.

Therefore, the probability that distinct keys $k, l$ collide is equal to the probability that $r \equiv s \pmod m$.

Lemma

$$\begin{aligned} \Pr_{h \in \mathscr{H}_{pm}}[h(k) = h(l)] &= \Pr_{0 \le r, s < p}[r \equiv s \pmod m] \\ &= \Pr[r \equiv s \pmod m \mid (r, s) \text{ are uniformly random in } \Z_p] \\ &\le \dfrac{\left\lceil \frac{p}{m} \right\rceil - 1}{p - 1}\\ &\le \dfrac{\frac{p+m-1}{m}-1}{p-1}\\ &= \dfrac{1}{m} \end{aligned}$$

Open Addressing

可参考「概率论」笔记。

Here's another way to resolve collisions except chaining.

Basic idea: On collision, probe a sequence of buckets until an empty one is found.

We redefine $h\colon U \times [m] \to [m]$, where the first $[m]$ means the probe number and the second one means table index.

HashInsert(T, k):
i := 0
repeat
    j := h(k, i)
    if T[j] == NULL or T[j] == DEL
        T[j] := k
        return j
    else i := i + 1
until i == m
error "overflow"

HashSearch(T, k):
i := 0
repeat
    j := h(k, i)
    if T[j] == k
        return j
    else i := i + 1
until i == m or T[j] == NULL
return NULL

HashRemove(T, k):
pos := HashSearch(T, k)
if pos != NULL
    T[pos] := DEL
return pos

Without DEL mark:

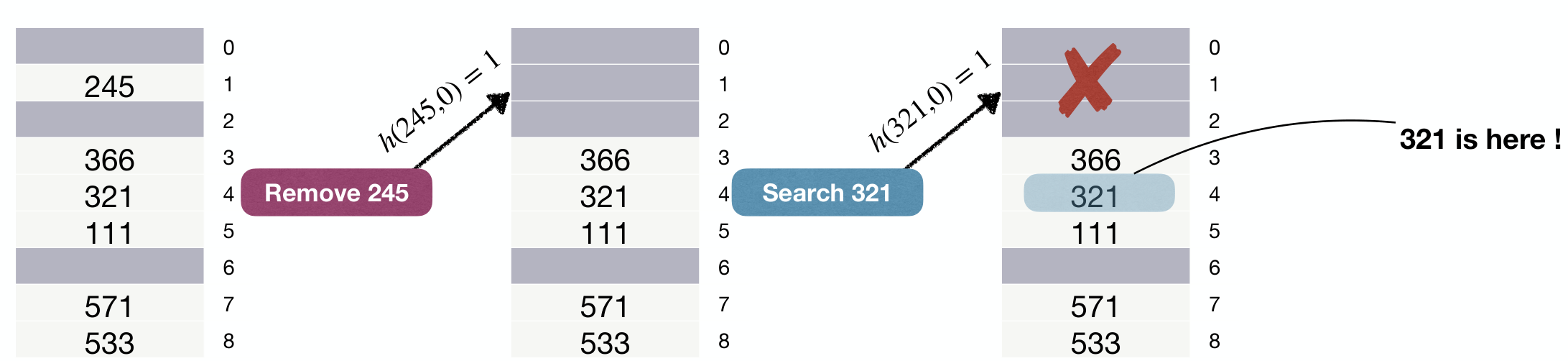
With DEL mark:

Linear Probing

$$h(k, i) = (h'(k) + i) \bmod m$$

where $h'$ is an auxiliary hash function.

Since the initial probe position determines the entire probe sequence, only $m$ distinct probe sequences are used with linear probing.

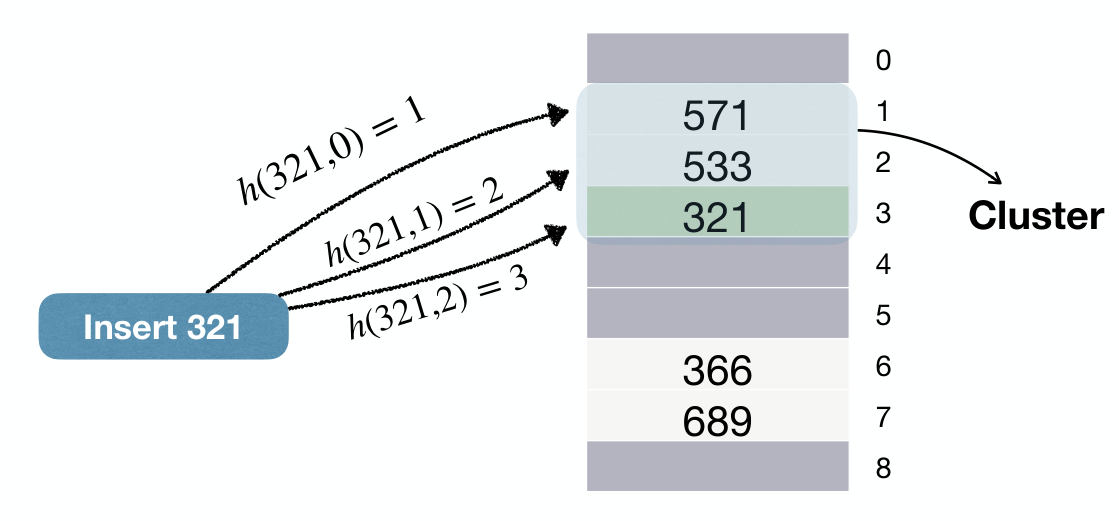
Another problem with linear probing is Clustering:

• Empty slot after a "cluster" has higher chance to be chosen.
• Cluster grows larger and larger.
• Cluster leads to higher search time in theory.

The remove mechanism (i.e., the DEL mark) causes "anti-clustering" effect, improving the performance of linear-probing hash tables.

Quadratic Probing

$$h(k, i) = (h'(k) + c_1 \cdot i + c_2 \cdot i^2) \bmod m$$

where $c_1, c_2$ are constants.

Problem: (Secondary) Clustering

• Keys having same $h'$ value result in same probe sequences.
• As in linear probing, the initial probe determines the entire sequence, so only $m$ distinct probe sequences are used.

Double Hashing

$$h(k, i) = (h_1(k) + i \cdot h_2(k)) \bmod m$$

where $h_1, h_2$ are auxiliary hash functions.

Why doubling? Observations:

1. If $h_1$ is good, $h(k, 0)$ looks random.
2. If $h_2$ is good, probe sequence looks random.

Linear and quadratic probing doesn't give observation 2.

The value $h_2(k)$ must be relatively prime to $m$ for the entire hash table to be searched. Conveniently, let $m$ be a prime number.

Otherwise if $m$ and $h_2(k)$ have greatest common divisor $d > 1$ for some key $k$, then a search for key $k$ would examine only $\dfrac{1}{d}$ of the hash table.

Each possible $(h_1(k), h_2(k))$ pair yields a distinct probe sequence. Therefore double hashing can use $\Theta(m^2)$ different probe sequences.

This is not the best. Uniform hashing gives the permutation of $m$ elements, which is $m!$.

Performance of Open Addressing

Let random variable $X$ be the number of probes made in an unsuccessful search. Then

$$\mathbb{E}[X] \le \dfrac{1}{1 - \alpha}$$

where $\alpha = \dfrac{n}{m}$ is the load factor.

Proof.

证明在「概率论」中就已经证过了，这里略。

Insight: Always make 1st probe, and make 2nd probe with probability $\approx \alpha$, 3rd probe with probability $\approx \alpha^2$, and so on.

Let random variable $X$ be the number of probes made in an successful search. Then

$$\mathbb{E}[X] \le \dfrac{1}{\alpha} \ln \dfrac{1}{1 - \alpha}$$

Proof.

Let $N_i$ be the expected number of probes made when searching the $i$-th inserted key.

Due to previous analysis, we have

$$N_i \le \dfrac{1}{1 - \frac{i-1}{m}}$$

Therefore

$$\begin{aligned} \mathbb{E}[X] &\le \dfrac{1}{n} \sum_{i=1}^{n} N_i \\ &\le \dfrac{1}{n} \sum_{i=1}^{n} \dfrac{m}{m - (i-1)} \\ &= \dfrac{m}{n} \sum_{i=0}^{n-1} \dfrac{1}{m-i}\\ &= \dfrac{1}{\alpha} \sum_{k=m-n+1}^{m}\dfrac{1}{k}\\ &\le \dfrac{1}{\alpha} \int_{m-n}^{m} \dfrac{1}{x} \d x\\ &= \dfrac{1}{\alpha} \ln \dfrac{m}{m-n}\\ &= \dfrac{1}{\alpha} \ln \dfrac{1}{1 - \alpha} \end{aligned}$$

Chaining v.s. Open-addressing

• Good parts of Open-addressing
  • No memory allocation
    • Chaining needs to allocate list-nodes
  • Better cache performance
    • Hash table stores in a continuous region in memory
    • Fewer accesses brings table into cache
• Bad parts of Open-addressing
  • Sensitive to choice of hash functions
    • Clustering is a common problem
  • Sensitive to load factor
    • Poor performance when $\alpha \approx 1$